Обоснование возможности использования формализованных подходов в вопросах выбора оптимальной стратегии развития компании

На настоящий момент времени, в научной литературе, посвященной проблемам стратегического развития компаний, трактовка выражения «механизм стратегического выбора», в контексте оптимального управления организацией или крупной компанией, носит неоднозначный характер, что приводит к необходимости аналитического представления обобщенных результатов анализа методик, используемых при выборе оптимальной управленческой стратегии, в рамках существующих в предметной области школ.

Работы [1, 2] выделяют научные школы, получившие не только теоретическое обоснование управленческой стратегии, но и их дальнейшую практическую реализацию. Результаты проведенного исследования оказывают существенное влияние на формулировку понятия стратегического выбора в рамках школ стратегического управления. В середине прошлого века в европейских странах

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

практически одновременно сформировались несколько направлений стратегического менеджмента, играющих ключевые роли в вопросах разработки и практической реализации стратегий. К ним отнесем школы моделирования, планирования, обучения и предпринимательства. Учитывая многоаспектность характера особенностей одного и того же объекта исследования, последователи любого из этих направлений придерживаются различных позиций в вопросе выбора и дальнейших перспектив в оптимального стратегического управления компанией.

Материалы и методы

В условиях неустойчивой экономики, обусловленной целям рядом объективных внешних факторов, наиболее часто в стратегии перспективного развития компании используется SWOT-анализ, использование такой методологии предопределено возможностью анализа и последовательной оценки как сильных, так и слабых сторон компании в различных средах, а также потенциальные перспективы и негативные результаты, которые должны быть просчитаны при анализе альтернатив и реализации стратегии выбора перспектив.

Укрупненный алгоритм стратегии выбора развития компании может быть представлен в виде соответствующей схемы (рисунок 1).

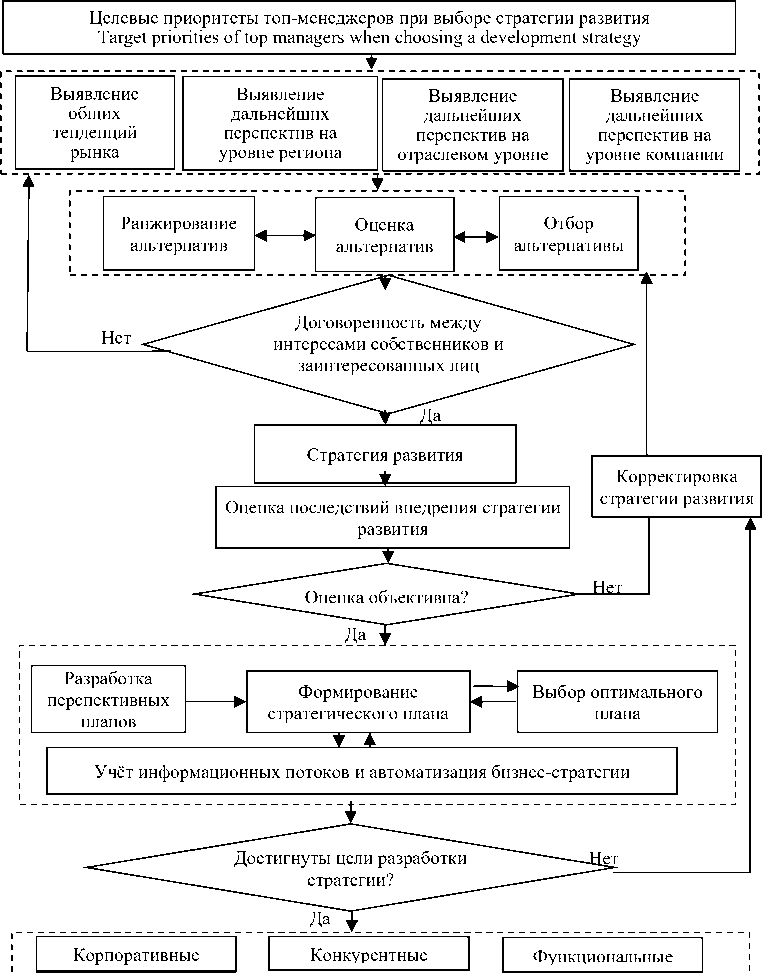
Рисунок 1. Схема алгоритм выбора стратегии развития компании

Figure 1. Diagram of the algorithm for selecting the company's development strategy

Достижение требуемого результата, предполагает построение SWOT-матрицы, подтверждающей возможность формировать стратегические альтернативы компании на основе учета внешних возможностей и рисков, а также анализа внутреннего потенциала.

Формирование подобной матрицы подразумевает определение совместных моментов, оказывающих наибольшее влияние на деятельность компании на настоящий момент времени, а также, моментов, оказывающих существенное влияние в перспективе и выделение среди них позитивных и негативных моментов [3]. Для определения уровня влияния внешних и внутренних моментов на устойчивое функционирование компании и раскрытия ее потенциальных рисков и перспектив используют не классическую SWOT-матрицу, а модернизированную, в которой позитивные моменты воздействия отмечаются знаком «+», негативные – знаком «–», моменты, оказывающие двойственное воздействие – «+/–», нейтральное воздействие – «0».

Позитивной стороной такого подхода к проведению стратегических исследований с учетом выбора наиболее оптимальных стратегических альтернатив, является то, что подобный анализ представляется многоцелевым инструментарием, которым, в рамках стратегического выбора, можно воспользоваться не только экспертами компании, но представителями внешних компаний, вне зависимости от размеров компаний и объемов, производимой продукции. Однако, при проведении анализа возможных рисков, велика вероятность того, что равновеликие параметры могут принять разное наполнение, т. к. они могут быть расценены как потенциально перспективными, так и оказывающими некую угрозу дальнейшему функционированию компании, что существенно препятствует дальнейшей реализации стратегических перспектив [4–5].

Следовательно, весьма целесообразным, является использование в качестве стратегического инструментария SWOT-матрицы, позволяющей учитывать многоаспектность проблемы, а также добавить нейтральную позицию. Отметим, что в качестве такой позиции целесообразно рассмотреть усредненное состояние компании на рынке в конкретной ситуационной составляющей.

Для каждой компании уточняется набор и уровень конкретизации исследуемых факторов, заполнение таблицы происходит с учетом того, что каждый фактор может быть оценен с учетом 3-x критериев (крепкий, нейтральный или слабый) и выделен по одному из них.

Заметим, что любая альтернатива представлена позитивной, интегрированной оценкой, отражающей внутреннее состояние компании с учетом ее среднерыночного состояния.

Проведение стратегического анализа внутреннего состояния компании показывает все положительные стороны SWOT-анализа, заметим, что такой подход позволяет выделить точку соответствующую ноль-точке конкурентной борьбы в конкретном рыночном секторе [6].

Следовательно, для реализации выбранной стратегии компания должна находиться в состоянии, в котором, по отношению к компаниям-конкурентам, по большинству показателей должен сохраняться нейтралитет и только по одному – она должна сохранять существенное преобладание.

Классические подходы решения управленческих проблем достаточно часто используют формулировки и оценки, основывающиеся на неопределенности в утверждениях, требованиях и лингвистических понятиях [7–8]. Такой подход существенно усложняет формализацию и построение имитационных моделей, базирующихся на количественной информации.

Количественная информация, на которой базируются имитационные модели, и происходит формализация, описывающая поведение системы в перспективе, может быть задана только ее оценочными значениями. Все эти нюансы приводят к тому, что формализованные подходы к описанию задачи только приблизительно описывают решаемую задачу [9]. Попытки использования вероятностных подходов при построении математических моделей сталкиваются с большими проблемами, возникшими из-за отсутствия статистической информации в должных объемах, что приводит к невозможности спрогнозировать будущее поведение системы, с учетом имеющейся информации, а также появляющихся дополнительных сложностей решения вероятностных проблем.

Использование в имитационных моделях вместо числовых характеристик их усредненных значений приводит при малых объемах статистической информации к получению решения не соответствующего первоначальной постановке задачи.

Определим i -й показатель эффективности нескольких различных альтернатив f ( A_r ) и f ( A ) через их соответствующие функции распределения:

Р {f. (Ar) ^ bk } = йи, Р {f (Ai) ^ bk } = Э,и или как:

Р { f ( A r К b k ’ b »¹ ]} = в »

и p { f ( A i ) e[ b » , b » ] } = в » , t = 0,1,... T .

Для нашего случая b и bt соответствует различным значениям конкретного i - го показателя эффективности, к = 1,...,K, а ви,вм — определяет вероятностные оценки альтернатив A и A , не превосходящих величину b или принадлежащих соответствующему интервалу значений.

При проведении анализа значений равнозначного показателя эффективности рассмотрим различные определенные величины, соответствующие:

– математическому ожиданию

Tt

Фи ( A r ) = mi { f ( A r ) } = 2 b ik Pu r ;

t = 1

b * = 1 ( b k ' + b i. ) ;

– среднеквадратическому отклонению

^Ф 2i ( A r- ) =     { ^fi ( A r ) } =

T                            2

=     2 mAfAA r ) } - ь*  PA;

T ¹ t = 1 ^L

– вероятности значению гарантирующему, что соответствующий показатель будет не выше некоторых предварительно заданных значений конкретного показателя:

^ф 3 qi ⁽ A r ) = P { fi ⁽ A r ) > ^b iq } =

= $ f ( x\A _r ) dx , g = 1,..., Q^

—ro ф4 gi( Ar ) = P {fi ( Ar )< dig } = ro

= I f i ( xA r ) dx , g = 1,..., G i .

-ro

Величину показателя, значение которого обеспечим с вероятностью, не меньше заданной предварительно, запишем как:

^ф 5 qi ( A r ) = { b iq | p [ fi ( A r ) >  b iq ] >  P iq } , g = 1,", ^Q2 ^ф 6 gi ( A r ) = { d ig | p [ fi ( A r ) >  d ig ] >  Y ig } , g = U G 2

Заметим, что в роли таких показателей можно рассмотреть моменты распределения высших порядков

T

Ф 7 i ( A r ) = S { f i ( A r ) } = £ m i { f i ( A r ) } - b i.

t=1 LJ

T ф8i ( Ar ) = R {fi ( Ar )} = T mi{Pi ( Ar )} — bik t=1 LJ

Pk r

Допустим, что условие <  или >  соответствует условиям приоритетности одной функции распределения случайной величины над другой в большую или меньшую сторону одного из значений [11–13].

Учитывая, что функции распределения i -го показателя эффективности альтернативы A соответствует абсолютный приоритет относительно функции распределения этого показателя альтернативы A .

P { fi ( A r ) > ^b . }^ P { fi ( Al ) > ^b ik } ,     ⁽¹⁾

только в случае выполнения неравенств из соответствующей системы:

d i ( A r ) > M Ai ) ; ^ф з qi ( A r ) > ^ф з qi ( A i ) , q = 1,..., Q;   ^

^ф 5 qi ( A r ) < ^ф 5 qi ( A l ) , q = U^ ^Q 2

^ф 2i ( A r ) >  ^ф 2i ( A l ) ; ^ф 4 qi ( A r ) >  ^ф 4 qi ( A l ) , g = 1,..., G 1 ; p^

^ф 6 qi ( A r ) < ^ф 6 qi ( A l ) , g = 1,..-, ^G 2

В случае не выполнения хотя бы одного из условий (1–3), можно говорить об относительном предпочтении. Запишем интегрированный показатель оценки распределения i-го критерия следующим образом:

Q 1

Vi( Ar ) = «ифи( Ar ) + 2 a3 qiф3 qi ( Ar ) + q=1

Q 2 G 1

¹ 2 ^a 5qi ^ф 5qi ( A r ) —« 2i ^ф 2 i ( ^Ar ) — 2 ^ 4 si ^ф 4gi ( ^Ar ) — ⁽⁴⁾ q = 1                                             g = 1

G 2

• — T a gi ^> gi{ A r ) ;

g = 1

G 1^G2

vi (Ar) = Ta4s-ф4gi (Ar) + 2a6giф6gi (Ar ) -g=1

• - «2ф21 (Ar ) — «2^2ii (Ar ) — «1i фИ (Ar ) —

Q 1 Q 2

• ^- 2 ^a 3q_l ^ф зqi ⁽ A r ) ^- 2 ^a 5gi ^ф 5gi ( A r ) .

q=1

причем 0 <  a _z<  1;   0 <  a_k <  1; k = 3,4,5,6,

• 5 = q = 1,.., Q 1 ;    5 = g = 1,..., G;   s = g = 1,..., G 1 ,

s = g = 1,...,G2, значения коэффициентов весов, удовлетворяющих условиям нормировки:

Q1          Q2          Q3

«11 + «21 + Ta3 qi +Ta5 qi + Ta4 qi + Ta6 qi = 1.

q=1          q=1          g=1

Учтем, что значения ф _gi ( A _r ) , ф _{2 gi} ( A _r ) , ф _{5 g}i ( A r ) , ф _{6 gi} ( A r ) представлены в единицах измерения конкретного показателя, то их использование в выражениях (4) и (5) подразумевает нормировку и их представление интервале [ 0,1 ] .

Специфика исходной постановки задачи приводит к тому, что ряд величин в суммарных оценочных показателях функции распределения могут вообще отсутствовать. Такой эффект может быть достигнут в предположении того, что значения соответствующих весовых коэффициентов Ost равными 0. На практике, наиболее часто встречаются следующие случаи:

• 1)    а_и = 1, при этом, остальные весовые коэффициенты равны 0, следовательно, будет учтено математическое ожидание функции распределения;

• 2)    а_и ^ 0, a_2i ^ 0, все значения оставшихся весовых коэффициентов равны 0, это говорит о том, что будет учтено только математическое ожидание и дисперсия.

Роль комплексных критериев оценки эффективности альтернатив может быть сыграна следующими компромиссными показателями:

n

F +(Ar )=Ё w^( Ar);

= 1

n

^F - ( A r ) = Ё w ^ -k A r ) ,

= 1

0 <  w <  1, i = 1,..., n;tw, = 1.

i = 1

Учтем, что альтернатива A , будет иметь относительный приоритет перед альтернативой A , если будут выполнены следующие требования:

A r > Re A , ^ F ⁺ ( A r ) > F ⁺( A l ) ;

A r < Re A , « F - ( A r ) < F -( A , ) ;

Далее, воспользуемся математическим подходом, основанном на использовании элементов нечеткой логики и нечётких интервалов. Такая методика, позволяют наиболее реалистично смоделировать существующую проблему и получить оптимальное решение [14].

Методы нечеткой логики в нахождении решения задач многокритериальной оптимизации служат дальнейшим продолжением детерминированных подходов в условиях, когда требуется выбрать наиболее оптимального решения из всех возможных альтернатив. Роль весовых коэффициентов локальных целевых функций в каждой альтернативе будет представлена соответствующим логическим термом. Помимо этого, некоторые ограничения из пространства принятия решений могут описываться на понятийном уровне.

Тогда задача многокритериальной оптимизации может быть записана терминами нечеткой логики. Любой альтернативе A эксперт ставит в соответствие нечеткое множество M k , которое соответствует степени оптимальности каждой из целевых функций в к онкретной альтернативе. Такое множество M k можно представить посредством функции принадлежности вида ц^f, ( XA ) ] : = f ( XA ) ^ [ 0,1 ] .

Заметим, что компромиссная альтернатива должна одновременно принадлежать пространству допустимых альтернатив, а также – пространству наиболее оптимальных решений.

Когда модель принятия решений подразумевает представление множества значений векторов локальных целевых функций Z = F(X) = ||Z|| и множества допустимых решений G = |G|| посредством использования нечетких множеств, то компромиссное решение D будем искать в виде нечеткого множества, принадлежащего пересечению первых двух нечетких множеств D е{Z1 HZ2П..Л Z, П..Л ZnAG^..^ Gm }.

Альтернатива A ^*, соответствующая требованию

^d [F (XIA* )]=mmrax ц» [F (XiAr)], определяет нечётко-оптимальное решение исходной постановки задачи [15].

Затем, представим нечеткие множества в виде интервалов, рассмотрев функ ци и принадлежности на множестве значений x е X, которые, начиная с некоторого значениях x = a_x , где ц ( а 1 ) = 0,, монотонно возрастают, достигают в некоторой точке x = m_x максимального значения ц ( т_х ) . Затем на некотором интервале значений m_x <  x <  m₂ с увеличением x сохраняют максимальное значение этой функции.

После этого при x >  m₂ с увеличением значения x функция принадлежности начинает монотонно падать, достигая при некотором значении x = а ₂ либо нуля, либо своего второго минимального значения.

Заключение

Подобная поведенческая особенность функций принадлежности позволила сформировать некую общую структуру этих функций, вычисленную с точностью до 4 параметров, позволяющих существенным образом модифицировать вид и значения функций в интересующих нас точках. К такому классу можно отнести треугольные, трапециевидные, экспоненциальные и другие виды функций принадлежности. Представление которых, можно сделать, используя левый, правый и центральный отрезки.