Обоснование выбора структур неоднородных иерархических систем с помощью аппарата генетических алгоритмов

Эволюционный поиск как метод оптимизации применительно к выбору сложной иерархической гетерогенной структуры системы позволяет эффективно решать сложные комбинаторные задачи оптимизации для построения и управления функционированием систем, обладающих сложной неоднородной иерархической структурой.

Среди методов эволюционного поиска для приближенного решения сложных комбинаторных задач оптимизации наибольшую эффективность показали генетические алгоритмы (ГА) [3]. Они представляют собой способы решения задач оптимизации на базе эволюционного моделирования и направлены на использование аналогий с природными процессами естественного отбора. Преимущества методов оптимизации на основе ГА в сравнении с классическими состоят, прежде всего, в возможности различных способов

Захаров И.В., Корчагин П.В. Обоснование выбора структур неоднородных...    105

задания целевой функции (ЦФ) и типов переменных оптимизации, а также в использовании вероятностных, а не детерминированных, правил поиска решений.

Метод с итерационной реализацией эволюционного поиска, включающий последовательное применение операторов кроссинговера, мутации, нормализацию формального описания генотипа, вычисление фитнесс-функций (ФФ), а также применение оператора селекции в каждой итерации, соответствующей поколению, предполагает настройку параметров алгоритма для получения удовлетворительного результата путем его неоднократной реализации с построенной предварительно ФФ [8]. В случае ограниченного времени решения задачи и ее существенной трудоемкости такой путь представляется весьма затруднительным. Поэтому для решения задачи стохастической комбинаторной оптимизации предлагается использовать ГА со стохастической ФФ с переменным (меняющимся в процессе поиска) коэффициентом вариации, проводя предварительный выбор рациональных параметров настройки алгоритма.

Рассмотрим подход к рациональному выбору структуры неоднородной информационно-вычислительной системы (ИВС), обеспечивающий наибольшее значение математического ожидания показателя ЦФ на основе ГА. Исходными данными для выбора являются электронная компонентная база (ЭКБ), которая может быть использована в качестве элементов ИВС, а также имитационно-аналитическая модель ИВС, соотносящая ее структуру с достигаемым показателем целевого эффекта, выступающим как ЦФ. Имеются ограничения по времени решения, что обусловлено трудоемкостью получения оценок значений ЦФ путем многократной реализации имитационного моделирования работы ИВС при исследовании множества решений. Соответствующая задача достаточно подробно изложена в [1].

Сущность применения ГА для решения поставленной задачи состоит в следующем [1; 8; 9]. Во-первых, кодируются варианты структуры и конструируются операторы ГА с учетом того, что роль элемента зависит от его места в структуре – другими словами, набор аргументов ЦФ является упорядоченным, в отличие от традиционных приложений ГА. Во-вторых, заданная ЦФ вычисляется посредством имитационно-аналитического моделирования [7]. Следовательно, для получения статистической оценки качества каждого варианта решения требуется получить значительное число ее реализаций. Поэтому на базе заданной ЦФ строится детерминированная фитнесс-функция, при помощи которой для заданного набора исходных данных проводится исследование вариантов построения ГА и его операторов. Сформулировав критерий качества ГА, можно подобрать его основные параметры, а также рациональное число реализаций ЦФ, соответствующих приемлемой трудоемкости. В частности, противоречиво стремление увеличить как число поколений, так и объем популяции. В-третьих, коэффициент вариации, зависящий от числа реализаций ЦФ, определяет не только ошибку ее оценки, но также результативность и скорость сходимости алгоритма, влияя на вероятность отбраковки перспективных решений. Существенно сократить вычислительную трудоемкость алгоритма можно за счет более грубой оценки математического ожидания ЦФ на начальных стадиях работы алгоритма (резко сокращая количество вычислений ЦФ) и более точной – на завершающих, обеспечивая точность результата.

Таким образом, новизна предлагаемого подхода к использованию ГА для решения задачи комбинаторной оптимизации в случае стохастической ЦФ подразумевает:

106 в ыпуск 2/2019

• •    адаптацию параметров ГА для конкретных исходных данных при детерминированной ФФ и последующую его реализацию при заданной ЦФ, предполагающей имитационное моделирование;

• •    снижение коэффициента вариации ФФ с ростом номера поколения, соответствующее уменьшению количества вычислений ЦФ со снижением номера поколения;

• •    применение различных параметров кроссинговера для аллелей, соотнесенных с элементами различных иерархических уровней структуры-фенотипа.

Приведем пример приложения разработанного метода и модели многомодульной перестраиваемой бортовой вычислительной системы космического аппарата в условиях деградации к выбору ее рациональной структуры. Построение модели функционирования системы изложено в [5; 7], представлена оценка ее адекватности, а также достигаемый при ее использовании эффект [5]. С этой целью разработаны и использованы соответствующие программные комплексы [4; 6], реализованные на ПЭВМ с тактовой частотой 3 ГГц в среде MatLab 7. При этом время вычисления однократной реализации ЦФ составило 274 мс для 100 шагов интегрирования, требуемое среднеквадратическое отклонение оценки ЦФ – 1%, что соответствует 10⁴ опытов (исходный коэффициент вариации ЦФ близок к 1). Общее число элементов трехуровневой структуры N = 22.

Проведены настройка и исследование соответствующего алгоритма. На рисунке 1 представлена зависимость результативности от объема популяции при фиксированной предельной вычислительной трудоемкости процедуры поиска оптимальной структуры.

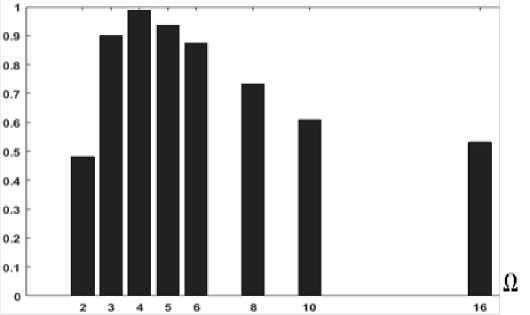
Рис. 1. Зависимость результативности от объема популяции при фиксированной трудоемкости

На рисунке 2 приведена экспериментальная зависимость показателя результативности поиска от числа поколений при рациональной настройке алгоритма: параметры кроссин-говера 0,95 … 0,8 в зависимости от уровня иерархии, параметр мутации 0,3, объем популяции 4. При этом коэффициент вариации ФФ изменяется от 0,4 в первом поколении до 0,01 в последнем.

При заданном ограничении по времени поиска, соответствующему перебору 48 вариантов структур традиционным путем, разработанный метод позволил отыскать квазиоп-тимальное решение, обеспечивающее значение оценки ЦФ около 0,99.

Захаров И.В., Корчагин П.В. Обоснование выбора структур неоднородных...    107

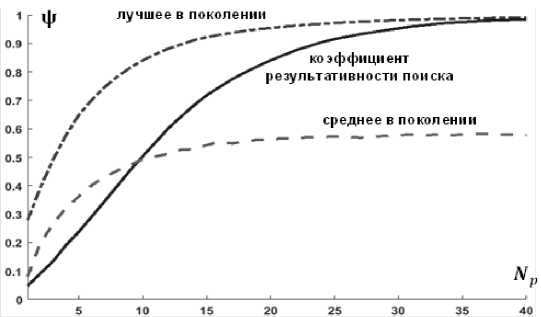
Рис. 2. Зависимость результативности от числа поколений при рациональной настройке алгоритма

В то же время для традиционного способа применения ГА (с постоянным коэффициентом вариации ФФ) с рациональными параметрами данная величина составила 0,56. С другой стороны, фиксируя требуемое значение оценки ЦФ, можно оценить выигрыш по времени его достижения: около 8 раз для величины 0,95 и 12 раз – для 0,9.

Таким образом, предложенный метод эвристического решения сложной комбинаторной оптимизационной задачи большой размерности, в основе которого лежит применение аппарата эволюционного моделирования – генетических алгоритмов, отличается эволюционным поиском со стохастической целевой функцией при структурно-параметрической оптимизации гетерогенных иерархически-сетевых ИВС. Данный метод позволяет существенно снизить вычислительную трудоемкость (в рассмотренном примере – приблизительно на порядок). Также в рассмотренном примере поиска структуры ИВС было получено приращение целевой функции при заданной трудоемкости до 90% относительно эвристического применения эволюционного поиска.