Обработка данных оптических триангуляционных сканеров для измерения профилей рельсов

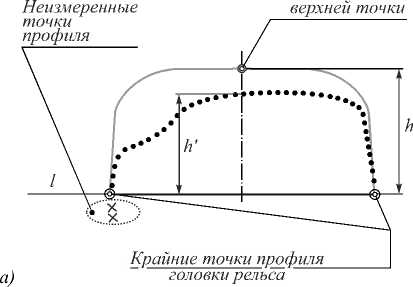
Введение Обеспечение безопасности движения на железной дороге является одной из важнейших задач. Контроль за состоянием пути и объектов железнодорожной инфраструктуры осуществляется с помощью специальных измерительных систем. Вагоны, оснащенные такими системами, называются путеизмерителями. Современные путеизмерители строятся на базе оптических триангуляционных сканеров, которые измеряют профиль рельса. С помощью анализа профиля определяются точки, которые используются для расчета параметров рельсовой колеи (рис. 1). ?     ПЛАТФОРМА или ТЕЛЕЖКА к__________________ Консоль __________________I Триангуля-/   1 х                  ______ '    \ Триангуляционный /    1 \                    1   \ ционный сканер /    1 \    ----------/        \ сканер Поле           I— зрения \            1 .сканера К' Шпала         9 х Рис. 1. Схема расположения триангуляционных сканеров относительно рельса Одним из контролируемых параметров пути является износ рельса. На российской железной дороге (РЖД) рассматриваются два основных износа: боковой (горизонтальный) и вертикальный износ, которые определяются путем сравнения измеренного профиля и профиля неизношенного рельса (рис. 2 а ). Тип рельса (на РЖД практически повсеместно используется рельс маркировки Р65) определяет высоту h и ширину головки рельса b . По измеренному профилю рельса вычисляется высота головки h' и прогнозируется положение верхней точки. Прямая l' параллельна пря-

мой l . Прямая l' располагается на 13 мм ниже верхней точки. Точки пересечения l' с профилем определяют расстояние b' . Вертикальный износ равен разности h – h' , а боковой износ – b - b' (рис. 2 б ). Боковой износ х          Ве ртикальный * \         \     износ Измеренный Г х//Д рельс         /У/, a) Пр огн озируем о е положение верхней точки 13 ллм~[                                    , :                     1,1               : / i1 | К райние точки п ро филя б)              головки рельса Рис. 2. Определение износов рельса Этот способ измерения имеет достоинство – простота вычислений. Однако он не лишен ряда недостатков с точки зрения измерений: – низкая точность измерений, так как крайние точки головки рельса могут не фиксироваться с необходимой точностью, что напрямую влияет на измеренные параметры (рис. 3 а );

– способ измерения не подходит для рельсов, изношенных не только с внутренней стороны, но и с внешней (так называемые «переложенные рельсы»); боковой износ будет равен сумме боковых износов с внутренней и внешней стороны колеи (рис. 3 б ).

Прогнозируемое положение

Боковой износ по внешней

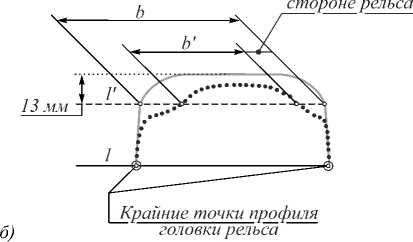
Рис. 3. Ошибки вычисления износов

Кроме методической составляющей, существует еще и технико-эксплуатационная проблема. Для формирования профиля рельса используется два сканера. Это приводит к усложнению конструкции измерительной системы, а также снижает ее надежность: измерения не будут проводиться, если отсутствуют данные хотя бы от одного из профильных сканеров.

Параметр надежности является одной из основных характеристик путеизмерителей.

Современные профильные сканеры обладают широким полем зрения, что позволяет получить профиль не только головки рельса, но и его шейки и подошвы. Эти элементы, в отличие от головки рельса, не подвергаются износу со стороны колесной пары. По ним можно провести совмещение измеренного профиля рельса с профилем неизношенного и определить износы.

В статье представлено два алгоритма для определения параметров совмещения, которые предназначены для измерительных систем, оснащенных только одним триангуляционным сканером ( примеч. : для измерения износов двух бортов необходимо два сканера вместо четырех).

Существующие работы в области обработки оптических сигналов триангуляционных сканеров

Работы по обработке профилей (объектов, представленных совокупностью точек), полученных опти- ческими триангуляционными сканерами, связаны с определением матрицы перехода [1] при заданных двух наборах точек, связанных между собой смещением, углом поворота и масштабными преобразованиями.

Одной из известнейших работ по определению параметров кривых второго порядка (эллипсов, парабол, гипербол) является работа [2]. Эта статья положила начало целому циклу работ разных исследователей [3–7].

В представленной работе рассматривается задача совмещения данных на плоскости, часть которых – это набор точек, а часть – совокупность уравнений, описывающих сложный контур. Эта работа является продолжением исследований, результаты которых описаны в статьях [8, 9].

Описание решаемой задачи

Профиль неизношенного рельса может быть описан отрезками прямых и дуг окружностей (рис. 4) [10].

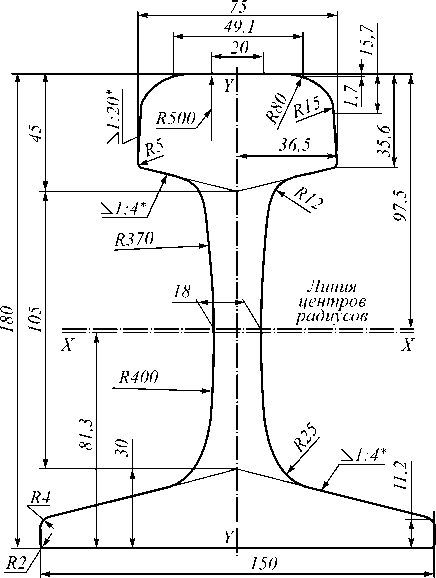
Рис. 4. Профиль рельса Р65 согласно ГОСТ 51685-2013

Задачу совмещения измеренного с помощью триангуляционного сканера профиля с профилем неизношенного рельса можно сформулировать различными способами.

Пусть будут даны точки на плоскости, соответствующие измеренному профилю. Точки образуют две совокупности с координатами ( p i , r i ) и ( w j , v j ), лежащие на различных отрезках прямых.

Совокупность точек ( p i , r i ) соответствует уравнению y = k 1 x + b 1 эталонного профиля, а ( w j , v j ) – уравнению y = k 2 x + b 2 .

Задача совмещения – найти такое преобразование, после которого точки ( p i , r i ) будут лежать на прямой y = k 1 x + b 1 , а ( w j , v j ) – на y = k 2 x + b 2 (рис. 5).

Измеренный рельс _______

Рис. 5. Совмещение профиля по отрезкам прямых

Участки (два отрезка прямой для совмещения с профилем неизношенного рельса

Второй способ совмещения основан на предположении, что совокупность точек ( p i , r i ) лежит на отрезке прямой y = kx + b , а совокупность точек ( w j , v j ) – на дуге окружности, описываемой уравнением x ² + y ² = R ², где R – радиус окружности (рис. 6).

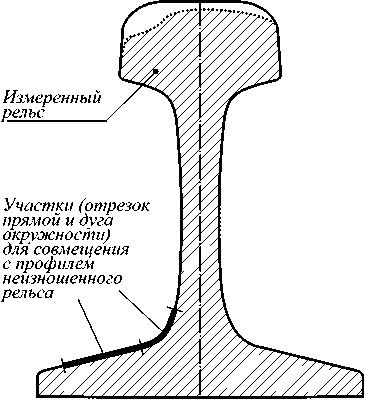
Рис. 6. Совмещение профиля по отрезку прямой и дуге окружности

Для обоих случаев были разработаны алгоритмы

совмещения.

Разбиение множества измеренных точек на подмножества

Для разработки алгоритмов необходимо, чтобы множество точек, измеренных триангуляционным сканером, было разбито на подмножества.

Для первого алгоритма необходимо выделить два участка с отрезками прямых, один из которых лежит на подошве, а второй – на шейке рельса. Для второго алгоритма – отрезок прямой, лежащей на подошве, и дугу окружности, лежащей на нижней выкружке рельса ( примеч. : выкружка – это вогнутый архитектурный облом, представляющий по очертанию четверть окружности или отрезок кривой, близкой к этой форме [11]).

На рис. 7 показан профиль измеренного рельса в системе координат триангуляционного сканера. Для каждой точки профиля вычисляется значение производной и кривизны с использованием соседних точек.

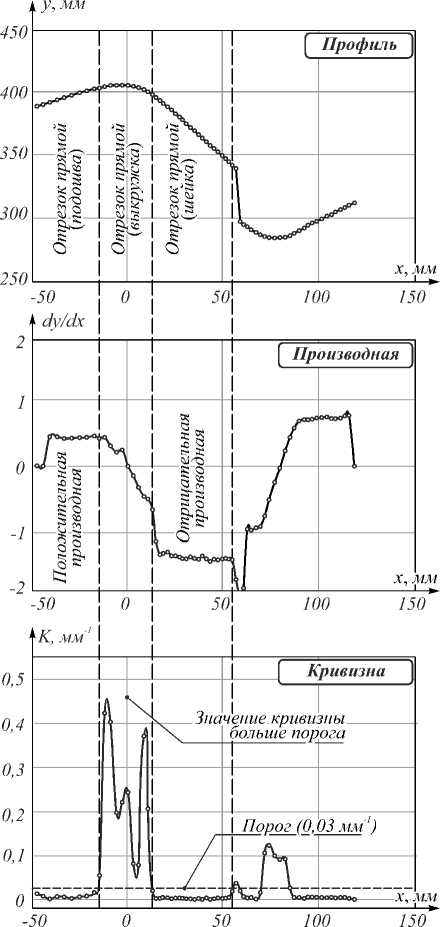
Рис. 7. Разбиение множества точек профиля на подмножества

Отрезок прямой, лежащей на подошве рельса, имеет положительную, а на шейке рельса – отрицательную производную. Кривизна на этих участках близка к нулю, в отличие от дуги окружности, лежащей на выкружке рельса.

Совмещение с профилем, заданным совокупностью прямых

Согласно вышеописанному, можно записать:

f p i 1 r i

1 ,

f cos ( a ) sin ^(a)

• - sin ^(a) x ⁰ If x-^? cos ^(a) y 0 ■ y, ;

0        1 JI 1 ,

^ wj^ гcos (a) - sin (a) x0 r j vj = sin (a)   cos (a) y0 yj ,             (2) v 1 v I 0 01 J I 1 7 где yi = k1xi + b1, yj = k2xj + b2.

Рассмотрим (1), из него можно выразить:

xi = cos (a)( pi- x 0) + sin (a)( ri - y 0),(3)

yi = - sin(a)(p, - x0) + cos(a)(г - y0).(4)

Перепишем эту систему уравнений, заменив A = cos ( a ), B = sin ( a ), A ² + B 2 =1.

xi = A (pi- x 0) + B (r- y 0),(5)

y=-B(Pi-x0) + A(Г -y0).(6)

Подставим найденные выражения в уравнение прямой y – k 1 x + b 1 =0, и для определения неизвестных параметров ( a , x 0, y 0) воспользуемся методом наименьших квадратов:

n f (A,B, x0, y0) = L{[-B(Pi - x0) + A(r - y0)]

i = 1

-k1 [A (pt - x0) + B (ri - y0)] + £1} ^ min, где n – количество точек.

df (A, B, x 0, y 0) dB df (A, B, x 0, y 0) dx 0

d f ( A , B , x 0, y 0 )

d y 0

A = V 1 - B ² ,

= N 1 - B + M 1 = 0,

= N 2 - x 0 + M 2 = 0,

= N 3 - y 0 + M 3 = 0,

N 1 = 2 IL ( p , - x 0 + k 1 ( r - y 0 ) ) x i = 1

x ( b - A ( r i - y 0 ) + A - k 1 ( p , - x 0 ) ) ,

M 1 = 2 L ( p , - x 0 + k 1 ( Г - y 0 ) ) 2 , i = 1

M 2 = 2 ]T ( B + A - k 1 ) 2 , i = 1

N 3 = 2 L ( A - B - k 1 ) - ( b - A - r i + B ( pi- x 0 ) + i = 1

+ k ( B - r i + A ( pi - x 0 ) ) ) ,

M 2 = 2 ^ ( A - B - k ₁ ) 2 .

i = 1

Таким образом, система уравнений запишется как:

N 1 - B + M 1 = 0;

N 2 - x 0 + M 2 = 0;

” N 3 - y 0 + M 3 = 0;

A = V 1 - B ² .

При выводе этой системы учитывались только точки ( p i , r i ). С учетом ( w j , v j ), выражение (7) перепишется как:

n f (A,B,x0,y0) = L{[-B(pi -x0) + A(ri -y0)]-i=1 '

- k 1 [ A ( p i - x 0 ) + B ( r - y 0 ) ] + b [} + + L { ^{[- B} ( w j ^{- x 0} )^{+ A} ( v j ^- y ⁰ )^]- j = 1

- k ₂ [ A ( w j - x 0 ) + B ( v j - y 0 ) ]+ b 2 } ^ min.

Соответственно выражение для коэффициента:

N 1 = ²LL ( p , - x 0 + k 1 ( r - y 0 ) ) x i = 1

x ( b - A ( r i - y 0 ) + A - k ₁ ( pi - x 0 ) ) +

+2]T (Wj - x0 + k2 (Vj - y0)) x j=1

x ( b ₂ - A ( v j - y 0 ) + A - k ₂ ( w j - x 0 ) ) .

Аналогичным образом изменятся формулы для M 1, N 2 и т.д.

Система нелинейных уравнений (8) решается итерационным способом, а алгоритм оценивания имеет следующий вид:

• 1.    Задается первоначальное приближение:

• 2.    По координатам ( p i , r i ), ( w j , v j ) и параметрам ( k 1 , b 1 ), ( k 2 , b 2 ), ( A , B , x 0, y 0) рассчитываются N 1, N 2, N 3, M 1, M 2, M 3.

• 3.    Рассчитывается:

• 4.    Присваиваем:

• 5.    Переходим к шагу №2.

x 0, y 0, B , A = V 1 - B ² .

M 1       M 2        M 3            2

B ‘ = --, x 0 ' =-- , y 0 ’ =-- , A     /1 - ( B ' ) .

N 1        N 2         N 3

A = A ‘ , B = B ‘ , x 0 = x 0 ’ , y 0 = y 0 ’ , a = arcsin ( B ) .

Количество переходов от шага №2 к шагу №5 определяет количество итераций.

Аналогично тому, как алгоритм проводит обработку двух совокупностей точек, он может быть расширен на три и большее количество.

Совмещение с профилем, заданным прямой и окружностью

С целью упрощения вывода алгоритма центр окружности был помещен в точку (0,0). В этом случае уравнение окружности запишется как x ² + y ² = R ², где R – радиус окружности.

Подставим в уравнение окружности выражения:

xi = cos ( a )( w i - x 0 ) + sin ( a )( v i - y 0 ) ,          (10)

y i = - sin ( a )( w i - x 0 ) + cos ( a )( v i - y 0 ) .        (11)

После раскрытия скобок и упрощений в уравнении будет отсутствовать параметр а :

( w j - x 0 ) 2 + ( v j - y 0 ) 2 = R 2 .                      (12)

Отметим также еще одну особенность в сравнении с предыдущим алгоритмом. Все три параметра x 0, y 0 и а в первом алгоритме были связаны между собой, поэтому параметры нельзя оценивать по отдельности друг от друга.

В рассматриваемом же случае возможна только их раздельная оценка, так как уравнение окружности (формула 12) не зависит от угла а , а уравнение прямой не связано с параметрами x 0, y 0 (можно найти бесконечное количество решений, связывающих между собой x 0, y 0 и а ).

Соответственно, по уравнению окружности проводится оценка x 0, y 0, а при фиксированных значениях x 0, y 0 по уравнению прямой проводится оценка угла поворота а .

Для вывода выражения для оценки x 0, y 0 рассмотрим следующий пример. Для оценки центра окружности достаточно иметь три точки: ( w 1 , v 1 ), ( w 2 , v 2 ), ( w 3 , v 3 ). Подставим их в выражение (12) и запишем систему уравнений:

( w i - x 0 ) 2 + ( v i - y 0 ) 2 = R ² ;

< ( W 2 - x 0 ) 2 + ( v 2 - y 0 ) 2 = R ² ;                    (13)

( W 3 - x 0 ) 2 + ( v 3 - y 0 ) 2 = R ² .

Приравняем уравнение 1 и 2, 1 и 3 системы (13), получим:

( W i

⁽ w i

- x 0 ) 2 + ( v ₁ - y 0 ) 2 = ( w ₂ - x 0 ) 2 + ( v ₂ - y 0 ) 2 ;

- x 0 ) 2 + ( v ₁ - y 0 ) 2 = ( w ₃ - x 0 ) 2 + ( v ₃ - y 0 ) 2 .

Приведем выражение (14) к эквивалентному виду:

2 ■ x 0 ( w - w ₂ ) + 2 ■ y 0 ( v ₁ - v ₂ ) = = ( W i² - W 2² ) + ( v i² - v 2² ) ;

2 ■ x 0 ( w - w ₃ ) + 2 ■ y 0 ( v _i - v ₃ ) = = ( w i² - w 3² ) + ( v i² - v 32 ) .

По методу наименьших квадратов можно записать:

NN                ₂

g(x0,y0) = ££(x0■ dwij + y0■ dvij + dwvij) , (i6) i =i j=i+i где dwi j = wi – wj, dvi j = vi – vj, dwvij = 0,5 ■ [(wi2 - wj2) + (vi2 - vj2)] ,

N – количество точек.

Решение выражения (16):

^d g ^{( x} 0, y ⁰⁾ ₌₀

dx0       , Jx0■ Aii + y0■ Ai2 = Bi, dg (x 0, y 0)      [ x 0 ■ A 2i + y 0 ■ A 22 = B 2;

-----------= 0;

d y 0

B i A 22 - B 2 ■ A 2i

Aii A 22 + ■ Ai2 ■ A 2i y 0 =

B 2 ■ A ii - B i A i2 A ii A 22 + ■ A i2 ■ A 2i’

где:

NN         NN

A ii = £ £ dw ij ² , A i2 = A 2i = £ £ dw j dv j , i = i j = i + i                                        i = i j = i + i

NN      NN

A 22 = £ £ dv ij² , B i = £ £ dw ij ■ dwv ij- , i = i j = i + i                        i = i j = i + i

B 2 = £ £ dv j ■ dwv ij . i = i j = i + i

При известных значениях ( x 0, y 0) можно оценить угол поворота а . Запишем уравнение, связывающее между собой координаты точек ( p i , r i ) и прямую y = kx + b .

k [[ cos ( а )( p i - x 0 ) + sin ( а )( г - y 0 ) ] + b -

-[- sin ( а )( p i - x 0 ) + cos ( а )( r i - y 0 ) ] = 0.

Введем обозначение: cp i = p i – x 0, cr i = r i – x 0 .

А тригонометрические функции разложим в ряд: cos ( а ) « i - 0,5 а ² , sin ( а ) «а .

Получим:

k |^ ( i - 0,5 а² ) ■ cp i + а ■ cr i ] + b -

-[-а- cp i + ( i - 0,5 а ² ) ■ cr ] = 0.

По методу наименьших квадратов получим: M g (а) = £{ k F(i - 0,5а2 )■ cpi +а- cr ] + b -i=i                                                   (i9)

• -[ -а- cp i + ( i - 0,5 а² ) ■ cr -] } ^ min,

где M – количество точек.

Решение уравнения (19):

d g (а)

' ' 0, L 0 + L 1 ■а + L 2 ■а ² + L 3 ■а ³ = 0, (20) да

M где L0 = 2£(cpi + cr ■ k)■(b-cri + cpi-■ k),          (2i)

i = i

M

L i = 2 £ ( cr i + cp i ■ k ) ■ ( b - cr i + cp i ■ k ) +

+ ( cp i + cr i ■ k ) 2 ,

M

^{L 2} = ² £ { ( cp i + cr i ■ k ) ■ ( cr i - cp i ■ k ) +

, i=i       .                   3

+ f cr i - + cp i- ■ k l■ ( cpi + cr ■ k ) L

I 2 2     J ^{v 7}J

E M Г cr cpr k )

I----— !■( cri- cpi^ k).

i=i V 22

Уравнение третьей степени решается в радикалах. Только один из корней будет являться вещественным числом, а два других – комплексными числами.

Если угол более 10°, то необходима итерационная процедура.

Итоговый алгоритм для оценки угла а выглядит следующим образом:

• 1.    Выбирается первоначальное значение угла поворота а k , к = 0.

• 2.    Рассчитывается матрица поворота:

• 3.    Рассчитываются координаты точек с учетом поворота:

  cp i = Mp ^- x 0 cr i         r i - x 0

  
  

• 4.    Рассчитываются переменные L 0, L 1, L 2, L 3 по формулам (21 – 24).

• 5.    Рассчитываются корни уравнения (20).

• 6.    Из корней уравнения выбирается один корень а , который является вещественным числом.

• 7.    Рассчитывается уточненный угол:

• 8.    Перейти к шагу №2.

cos ( а к ) sin ( а к ) - sin ( а к ) cos ( а к )

cos ( а _к )    sin ( а _к )    p i - x 0

•

- sin ( а _к ) cos ( а _к ) [ r - x 0

к = к +1, а к = а ы + а .

Количество переходов определяет количество итераций. Выход из процедуры происходит по критерию: | а к - а к —i |< thr , где thr - порог. При моделировании использовался порог, равный 10^–9 рад.

Компьютерное моделирование и натурный эксперимент

Для определения точности измерения параметра бокового износа была использована модель профиля рельса с изношенной головкой и известным значением бокового износа.

К каждой координате точки данного профиля по абсциссе и ординате добавлялась помеха с Гауссовым распределением и заданным среднеквадратичным отклонением (СКО) о n .

Согласно вышеописанным алгоритмам проводилось совмещение с неизношенным профилем рельса и вычислялся боковой износ.

Вычисленное значение бокового износа сравнивалось с действительным значением. Результатом сравнения является среднеквадратичная величина (СКВ).

Результат точности измерения представлен на рис. 8.

На рис. 9 показан процесс измерения профиля рельса с использованием профильного сканера, где яркая линия на поверхности исследуемого объекта соответствует лазеру сканера.

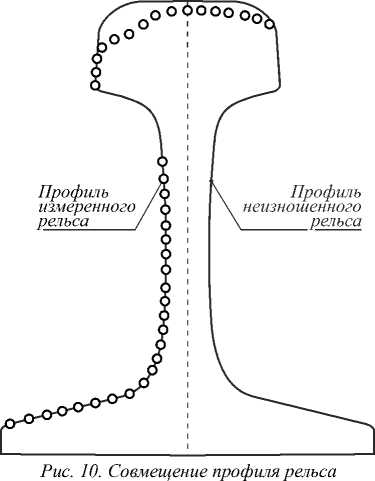
На рис. 10 показан результат совмещения измеренного профиля рельса с профилем неизношенного рельса в соответствии с предложенными алгоритмами.

Заключение

Разработка алгоритмов совмещения профилей является одной из задач в тех областях науки и техники, в которых применяются триангуляционные профильные сканеры. Контроль износов для обеспечения без- опасности движения на железной дороге является одним из примеров практического применения разрабо-

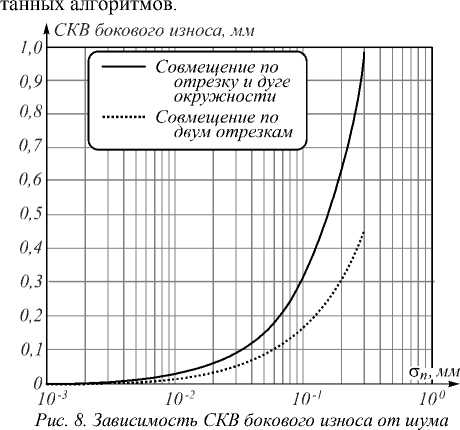
Рис. 9. Получение профиля рельса профильным сканером

с профилем неизношенного рельса

Предложенные алгоритмы потенциально обеспечивают улучшение технико-экономических показателей путеизмерителей (использование в системе измерения одного сканера вместо двух без ограничения их функциональных возможностей), а также улучшение эксплуатационных показателей (вероятность выхода из строя одного из двух сканеров выше, чем одного).

Следует отметить, что разработанные алгоритмы можно использовать для контроля качества изготовления деталей, а также степени их изношенности для их своевременной замены. Эта задача возникает в тех областях промышленности, в которых необходимо контролировать геометрию объектов со сложным профилем, то есть состоящим из отрезков и дуг окружностей (например, автомобильные фары, пазы в трубах, замковой резьбы бурильных труб и т.д.).