Обработка данных в задачах электрофореза

Информационные сигналы, полученные с детекторов прибора, как правило, подлежат первичной и вторичной обработкам. К первичной обработке относят методы оценивания информационных параметров, к вторичной — математическую обработку и анализ. Одной из распространенных задач является задача поиска экстремальных точек. Точкой локального экстремума называют такую точку x , для которой существует число 5 > 0 такое, что F ( x ) <  F(у ) для всех у е N ( x *, 5 ), у ^ x [1] (для минимума) или F ( x ) > >  F ( y ) (для максимума).

Однако в реальных физических экспериментах, где всегда имеются шумы, такое определение вряд ли подходит, т. к. большинство точек являются экстремумом (максимумом или минимумом). Именно поэтому необходимо применять процедуры сглаживания и фильтрации при первичной обработке. Эти методы могут применяться для широкого круга задач.

В работе рассматриваются методы поиска экстремумов для задач капиллярного электрофореза. Экстремумами в таких задачах являются пики, а анализ состоит в обнаружении и расчете их параметров, в том числе временных. Пиком в таких задачах можно назвать набор последовательных точек, значения которых значительно превышают значения точек вне этого набора. Анализ данных с помощью программного обеспечения, поставляемого с приборами капиллярного электрофореза, часто базируется на уже существующем и доказавшем свою пригодность алгоритме для высокопроизводительной жидкостной хроматографии [2].

ОПИСАНИЕ АЛГОРИТМА ПОИСКА ЭКСТРЕМУМОВ

В этом предлагаемом алгоритме определение пиков основано на изменениях первой производ- ной сигнала. Пик считается обнаруженным, когда первая производная превысит некое пороговое значение, которое нужно установить в соответствии с заданными критериями (рис. 1). Действительное время начала пика определяется точкой, где первая производная равна нулю. Конец пика определяется аналогично. Достоверность этого алгоритма зависит от правильного выбора порогового значения производной и реальной ширины самого пика [2].

Как правило, в электрофорезе пик имеет Гаус- ( ^x - ^x 0 ⁾² 2

сову форму, т. е. f (x) = a 1 • e 20 . Максимум первой производной достигается в точке x = x 0-o.                     (1)

Максимальное значение производной в этой точке будет f _max = a 1 • V e / o . Следовательно, пороговое значение первой производной выбирается таким, чтобы оно было меньше, чем a 1 • V e / o для всех пиков.

Как показывает практика, в капиллярном электрофорезе часто возникают ситуации, когда появляются небольшие отрицательные шумовые выбросы сигнала в окрестности точек, где первая производная превышает пороговое значение (рис. 2). Эту точку легко принять за конец пика, т. к. первая производная меняет знак и, следовательно, проходит через нуль. В такой ситуации центр пика будет определен заведомо неправильно. Для устранения этого недостатка необходимо применять предварительное сглаживание данных.

Для сглаживания данных существует множество методов. Здесь будет рассмотрен довольно простой метод Савитского—Голая. Метод применяется для серии данных f i = ft i ), где t i = 1 ₀ + i-h и i — целое число. Каждое значение данных f_i заменяется линейной комбинацией g i самого значения и значений нескольких соседей, т. е.

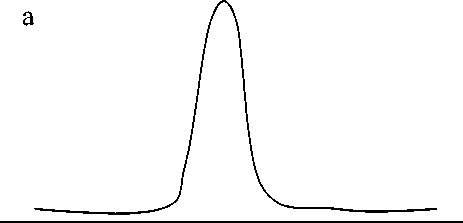
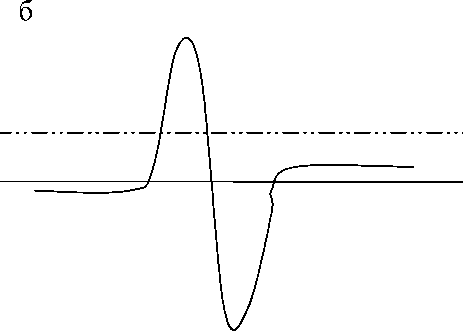
Рис. 1. Выбор порогового значения.

а — сигнал-пик; б — производная от сигнала; штрих пунктирной линией обозначен порог обнаружения пика

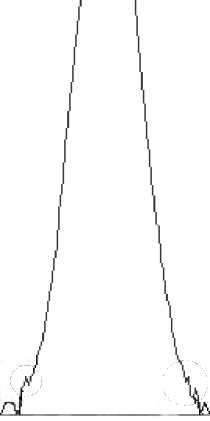
Рис. 2. Шумовые выбросы на фронтах сигнала

nr

81 = XCnfi+n ’ (2) n=-n где Ui — число точек слева от точки i, а nr — справа. В простейшем случае — это усреднение значения, если cn = 1/(nl + nr + 1). В случае, когда подвергаемая сглаживанию информационная зависимость является линейной, метод не вносит искажения. Что касается величин локальных максимумов, то метод всегда уменьшает максимальное значение функции. Наиболее подвержены искажению узкие пики, которые менее всего походят на линейную функцию в пределах соседних точек. Можно показать, что такие экстремумы после применения сглаживания становятся не только меньше, но еще и незначительно увеличиваются по ширине.

Если пренебречь увеличением ширины пика, то критерием для выбора числа соседей n в данном методе сглаживания будет g* > kf(x ₀), где g*— значение для точки максимума, вычисленное из (2), k — величина допустимого уменьшения экстремума и f ( x 0 ) — реальное значение экстремума.

Главным недостатком алгоритма поиска экстремумов высокопроизводительной жидкостной хроматографии является его смещенность. В алгоритме находится не точка экстремума, а точка, где первая производная превышает пороговое значение. Смещение будет всегда больше, чем а, т. к. максимум первой производной достигается в точке x ₀ - о согласно (1). Таким образом, метод нуждается в процедуре уточнения центра экстремума.

Если форма пика известна, то наиболее эффективным методом нахождения его центра и прочих параметров является метод наименьших квадратов. Метод обладает свойством оптимальности, состоящим в том, что он дает несмещенные оценки, имеющие минимальную дисперсию [3].

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПИКА

Если f ( t ) = x 1 • e^{x 2 (} t ^{x з )} и имеется набор измерений f i , то задача сводится к поиску

m min F(xi,x2,x3) = X(f--xi • ex2(t-xз)2)2.    (3)

^x 1 , ^x 2 ’ ^x 3                                i = 1

Эта задача носит название нелинейной задачи наименьших квадратов [4]. Задача оптимизации состоит в минимизации F ( x ).

Нам необходимо найти такую точку x* , что F ( x ) <  F ( x ) для всех допустимых точек x , которые близки к x ^* . Такая точка называется локальным минимумом.

Алгоритмы для минимизации функции n переменных разрабатываются уже свыше 140 лет.

Наиболее распространенными являются метод наискорейшего спуска и многомерный метод Ньютона.

Метод наискорейшего спуска был предложен Коши в 1845 г. Суть метода состоит в следующем. Обозначим вектор ( x 1 ,., x n ) T через x и предположим, что функция F ( x ) имеет непрерывные частные производные нескольких порядков. Для фиксированного x и меняющегося а совокупность векторов ( x , -а V F) представляет собой луч, исходящий из точки x . Известно, что - V F ( x ) — это направление "с холма" для функции F ( x ) [4], т. е. для достаточно малого положительного значения а значения функции будут убывать: F ( x - а VF) <  <  F ( x ) [4]. После этого ищется значение а (0 < а < ”), минимизирующее F в направлении - V F ( x ) . Это уже одномерная минимизация. Найдя этот минимум, начинают поиск вдоль полупрямой наискорейшего спуска, исходящей из новой точки x [4].

Достоинство метода наискорейшего спуска заключается в том, что он всегда сходится, если функция F ( x ) имеет непрерывные производные. Но в некоторых случаях он сходится довольно медленно (иногда требуется более ста итераций).

Этого можно избежать, применяя п- мерный аналог метода Ньютона. Функция F записывается в виде

F ( x ) = F ( x ) + p T V F ( x ) +

^{+ 1} P T ^{V 2} F ⁽ x ) p = F ⁽ x ) + Q ⁽ p ).         (4)

Чтобы получить шаг p , минимизируется квадратичная функция Q ( p ), при помощи построения ее градиента по p

V _PQ ( p ) =

= ^V p ( P T ^V F ( x ) + 2 p T ^{V 2} F ( x ) p ) =

= F ( x ) + V ² F ( x ) p .                       ⁽⁵⁾

Приравнивая его к нулю, получаем

V ² F ( x ) p = - V F ( x ) .                   (6)

Это система n линейных уравнений относительно n неизвестных p = (p 1 , p ₂,..., p_n ) T .

Итак, x k+ 1 = x k + p = x k - V ² F ( x k ) ^- 1 V F ( x k ) .

Метод Ньютона в n- мерном случае обладает тем же свойством быстрой сходимости, что и в одномерном случае, а именно он сходится квадратично в окрестности решения:

Ilx k+i- x'lI,s e x k—xt •              <7> где в — некоторая неотрицательная константа, зависящая от F(x).

Но, как и в одномерном случае, у метода Ньютона есть недостатки. Например, он может не сходиться. Но если матрица V ² F ^{- 1} положительно определена, т. е. удовлетворяет условию z T V ² F ^- * z для всех z ^ 0, то в этом случае направление метода Ньютона гарантированно будет направлением спуска [4].

Недостатком метода Ньютона является необходимость вычислять матрицу вторых производных. Другой недостаток заключается в том, что вычисление шага p требует решения системы n линейных уравнений. Метод наискорейшего спуска не страдает этими недостатками, но он приводит к большим потерям в скорости сходимости [4].

Для того чтобы получить альтернативные эффективные и практичные методы, можно аппроксимировать гессиан в ходе минимизации функции. Эти методы основаны на аппроксимации гессиана секущими и являются обобщением метода секущих. Если B_k = V ² F_k = F ( x ), то шаг на k" й итерации будет определяться из системы

B k • p = - V F k . (8)

Таким образом, мы получаем вариант метода Ньютона, в котором используется приближенный гессиан. Новая аппроксимация гессиана выбирается так, чтобы

B k+ i ( x k+ 1 - x k ) = V F k+ 1 - V F k . (9)

В одномерном случае это однозначно определяет B _k+ 1 . При более высоких размерностях, для того чтобы определить B _k+ 1 , необходимы дополнительные условия.

Поскольку нам необходимо на каждой итерации вычислять обратную матрицу B ^-1 , можно еще упростить метод Ньютона, используя алгоритм Шермана—Моррисона для приближенного вычисления обратной матрицы. Предположим, что для матрицы B _k вычислена обратная B _k ^{- 1} . Пусть на следующей итерации матрица

B k+ 1 = B k - wv T , (10)

где u и v — векторы размерности n . Тогда матрицу B -+ 1 можно вычислять по формуле

B-^ = B-1 + a (B-1u)( v TB-1), (11) k +1 k k k где a = 1/(1 - v T Bk1u). Это будет стоить O(n2) арифметических операций по сравнению с O(п3) операций при стандартном вычислении новой обратной матрицы.

ЗАКЛЮЧЕНИЕ

В статье описан метод для обработки информационных данных в капиллярном электрофорезе. Метод позволяет обнаружить и определить параметры пиков. Для определения параметров пиков использовался аналог метода Ньютона, в котором не требуется ни вычисления вторых производных, ни решения систем уравнений.