Обработка дискретной последовательности сложных сигналов с линейной частотной модуляцией для обнаружения и оценки радиальной скорости подводной цели

Цитирование: Шостак С. В. Обработка дискретной последовательности сложных сигналов с линейной частотной модуляцией для обнаружения и оценки радиальной скорости подводной цели / С. В. Шостак, А. В. Бенгард, Г. В. Дорофеев, П. А. Стародубцев // Журн. Сиб. федер. ун-та. Техника и технологии, 2024, 17(5). С. 678–682. EDN: AXASTR

F

В выражениях (1) и (2) f 1 – начальная частота первого сигнала, ^ ~ T – коэффициент девиации, F – полоса частот, T – длительность сигнала, f ₂ – начальная частота второго сигнала, f 1 >  f 2 .

На рис. 1 представлены мгновенные частоты сигналов s ₁( t ) и s ₂( t ). Мгновенная частота s ₁( t )

A(0 = fi+bt;(3)

мгновенная частота s ₂( t )

Ш = {г-Ы.(4)

Дискретная последовательность из s ₁( t ) и s ₂( t ) имеет вид

s(t) = MOSzO)]-(5)

Для обработки последовательности (5) воспользуемся одним свойством, характерным для сигналов вида s 1 ( t ) и s 2 ( t ), для чего смешаем (перемножим) их

z(t) = s1(t) ■ s2(t) = cos[2?r(At + 0,5bt2)] ■ cos[2?r(At — 0,5At2)] =(6)

= 0,5 cos[2tt(A + /2)t] + 0,5cos[2tt(A — /2)t + bt2)] = z1(t) + z2(t), где z^t) = 0,5 cos[2?r(/i + /2)t];(7)

z2(t) = 0,5cos [2тг(А - A)t + bt2)].(8)

Из полученных выражений (7) и (8) видно, что мгновенная частота z ₁( t ) имеет вид

Ai = (A+/2),(9)

т.е. постоянное значение, а мгновенная частота z ₂( t )

2F fz2 = (A - A) + 2bt = (A - f2) + yt(10)

с начальной частотой ( f 1 – f 2 ) и полосой 2 F на длительности одного сигнала T .

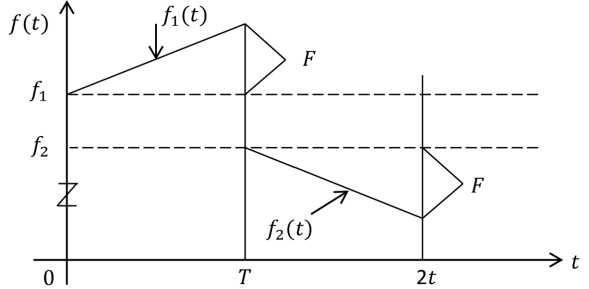
Рис. 1. Мгновенные частоты сигналов s ₁( t ) и s ₂( t )

Fig. 1. Instantaneous signal frequencies s 1 ( t ) and s 2 ( t )

Полученные составляющие z ₁( t ) и z ₂( t ), как легко заметить, находятся в различных частотных полосах, что позволяет проводить их обработку раздельно.

Рассмотрим теперь случай, когда цель подвижна. В этом случае временной масштаб эхо-

2 Up сигналов изменяется: t -> at = (1 ± —)t, где vp – радиальная скорость цели, c = 1500 м/с – скорость звука в воде, т.е. имеется доплеровская трансформация масштаба времени [1, 3].

Легко показать, что (7) и (8) приобретают вид zt(t) = 0,5 соз^тшСД Ч-ДХ]

z2(t) = O.Scos^TraC/! - /2)t + a2bt2)].                                (12)

Из выражения (11) следует, что так как cos |2тг ^1 ± —j (Д + /2)tj = cos |2tt ^1 ± —-J Д t|,                  (13)

2 v где fΣ = f1 + f2, то доплеровское влияние представляется как сдвиг fΣ на + —~ fx . Это позволяет c определять радиальную скорость цели, проводя спектральный анализ составляющей z1(t).

Из (12) видно, что z ₂( t ) – это низкочастотный ЛЧМ-сигнал с удвоенной полосой 2 F и с масштабом времени, преобразованным под действием эффекта Доплера. Для обработки такого сигнала следует применять корреляционные методы анализа. Реплики (опорные сигналы) в нашем случае получаются на основе выражений (11) и (12). Для этого следует использовать выражения

435(2F)

((Л-Л) + 2Г)/2

T^F)

которые показывают, как соотносятся параметры зондирующего сигнала и радиальной скорости цели в узкополосном (14) и широкополосном приближении (15), когда максимум корреляционной функции уменьшается на –3 дБ [1].

Рассмотрим возможную реализацию полученных результатов в виде устройства. На рис. 2 приведена структурная схема устройства.

Устройство содержит линию задержки ЛЗ (T) на длительность одного сигнала последовательности T, перемножителя, которые предназначены для реализации выражения (6), полосового фильтра (ПФ) с центральной частотой (f1 + f2) для выделения z1(αt), блока спектрального анализатора, где вычисляется спектральная плотность сигнала z1(αt) с оценкой радиальной скорости. В состав устройства также входит низкочастотный фильтр (НЧФ) для выделения составляющей z2(αt), коррелятор с банком реплик, по результатам функционирования которых обнаружитель выделяет сигналы после сравнения с порогом. При этом разрешающая способ- ность по дальности пропорциональна .

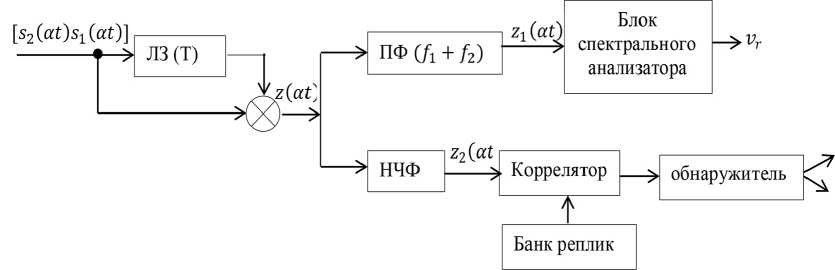
Рис. 2. Структурная схема устройства обработки дискретной последовательности [ s 1 ( t ) s 2 ( t )]

Fig. 2. Block diagram of a discrete sequence processing device [ s ₁( t ) s ₂( t )]

Одиночные сложные сигналы с линейной частотной модуляцией широко используются в современных и перспективных гидроакустических системах для обнаружения подводных целей и оценки их радиальных скоростей. Обработка таких сигналов проводится методом корреляционного сравнения. При этом естественно стремление получить более высокие точности измерения дальности, разрешающей способности по дальности, которые обратно пропорциональны полосе частот сигнала, и оценку радиальной скорости цели, которая оценивается косвенно по корреляции эхо-сигнала и соответствующей реплики. В представленной работе изложен способ обработки дискретной последовательности сложных сигналов с линейной частотной модуляцией. За счёт сдвиговых преобразований в процессе обработки получены низкочастотный сигнал с линейной частотной модуляцией и удвоенной полосой частот и гармонический сигнал с частотой из суммы двух начальных частот, составляющих последовательности. Применение такого преобразования позволяет существенно увеличить частотную полосу анализа, что значительно улучшает разрешающую способность по дальности, а наличие гармонического сигнала постоянной частоты даёт возможность оценивать радиальную скорость с достаточно высокой точностью.