Обработка информации комплексом нейронных сетей в распределённых волоконно-оптических измерительных системах

Процесс непрерывного развития науки и техники требует наличия совершенных измерительных технологий. Интенсивное развитие и внедрение волоконнооптических телекоммуникационных систем привело к появлению одной из наиболее динамично развивающихся областей оптоэлектроники – волоконнооптических датчиков физических величин [1, 2]. Волоконно-оптические измерительные устройства [3] обладают высокой чувствительностью к широкому классу физических величин и, в частности, к различным параметрам электрических, магнитных, температурных, акустических и деформационных полей.

Сегодня наукоёмкое производство не обходится без постоянного контроля за динамикой поведения множества параметров различных физических величин и физических полей (ФП). Решить эту задачу призваны информационно-измерительные системы, имеющие различную топологию и организацию, построенные, например, на волоконно-оптической элементной базе.

Использование измерительных технологий на основе волоконной оптики для создания сенсорных систем в ряде случаев является более перспективным благодаря тем преимуществ ам, которыми обладают волоконно-оптические чувствительные элементы по сравнению с их аналогами.

Распределённая информационно-измерительная система содержит распределённую волоконно-оптическую измерительную сеть (ВОИС), систему обработки измерительной информации, устройство хранения и представления информации.

ВОИС представляет собой набор волоконнооптических измерительных линий, уложенных в соответствии с определённой схемой на исследуемой поверхности. Задача восстановления параметров распределённых ФП по характ еристикам оптического излучения, проходящего по ВОИС, является томографической [4].

Для восстановления функци й распределения ФП с помощью ВОИС измерительные линии (ИЛ) укладывались по четырём направлениям (рис. 1). Для этой схемы характерна малоракурсность [5].

Рис. 1. Параллельная схема укладки измерительных линий в ВОИС

При использовании измерительных сетей возникает проблема обработки томографических данных, так как все приемлемые алгоритмы реконструкции распределений исслед уемых физических полей [6] являются итерационными, что не позволяет создавать быстродействующие информационно-измерительные системы даже при применении параллельных принципов организации вычислительных сетей.

Поэтому основное внимание в этой работе уделено процессу обработки измерительной информации, который, в свою очередь, заключается в последовательном выполнении двух процессов: оптимизации геометрии измерительной сети и предобработки с помощью набора заранее обученных нейронных сетей (НС).

Выбор нейросетевых методов определяется их быстродействием, способностью к обучению, обеспечивающей выполнение практически любого преобразования данных, даже в том случае, если оно не может быть описано определённой ф ункциональной зависимостью. Адаптивность нейросистем, вытекающая из способности к обучению, позволяет осуществлять подстройку вычислительной системы под изменения параметров решаемой задачи.

След ует заметить, что нейронные сети не подходят для томографии при большом числе проекций, поскольку число переменных в задаче о восстановлении является чрезвычайно большим. Однако в задачах с РВОИС проекционных данных намного меньше и это даёт возможность использования НС.

1.    Основные определения и обозначения

Пусть f = f ( x 1 , x 2 ) - вещественная положительная фун кция двух переменны х, описывающая ис-след уемы й объект. Далее б удем предполагать, что f бесконечно дифференцируема и имеет компактный носитель.

Двумерное преобразование Радона отображает функц ию f во множество её линейных интегралов.

Пусть индекс i определяет направление сканирования ф i , индекс j определяет отсчёт s ij в выбранном i -м направлении. В этом случае паре индексов ( i, j ) соответствует прямая линия L ij , вдоль которой сканируется область. Тогда значение проекции вдоль прямой L ij можно записать как

gj =^j f = j f (x1, x 2 ) d 1,                    (1)

Lij где ^ - преобразование Радона функции f, а d 1 -приращение вдоль прямой Lij.

Пары чисел (фi, sij), определяющие параллель- ную схему сканирования на плоскости.

ВОИС могут быть использованы для исследования различных свойств объектов окружающего пространства. Этой цели в наибольшей степени удовлетворяют сети матричного типа. Разобьём исслед уе-мую область S с R 2 на малые элементарные ячейки S k (элементы изображения) так, чтобы

N

S = U S k .

к =1

Считаем ф ункцию f постоянной в каждой ячейке S k и равной f k , символом f также обозначается и матрица, соответствующая этому разбиению:

f =	' fx         f 2      • f m +1       f m +2    • • • •                           • • •                 •	f m - f 2 m •
	4 fn ( m -1)+1     f n ( m -1)+2	f J nm у
	e

F = ( f f 2 - f™

fm + 1   - f 2 m  -   f nm ) •

В соответствии с выбранной схемой укладки измерительных линий интегральные уравнения (1) преобразуются в СЛАУ (сист ему линейных алгебраических уравнений) вида:

AF= G .                                     (3)

В системе (3) столбец неизвестных F = ( f 1 , ... ,f mn )^т высоты mn, соответствующий матриц е f вида (2), последовательно составлен из строк матрицы f .

В правой части матричного уравнения (3) стоит столбец проекционных данных размера

М = y ( 1 ) + ... + y ( i ) + ... + y ( P ) , который имеет вид:

G =( g 11 , …, g 1 _γ ( 1 ) ;…; g_i 1 , …, g_{i γ} ( _i ) ;…; g_p 1 , …, g_{p γ} ( _p ) ) , (4)

где y ( i ) — число ИЛ в i -м направлении.

Коэффициенты столбца (4) представляют собой линейную комбинацию неизвестных элементов f 1 , ... , f mn , с коэффициентами, значения которых определяются матрицей схемы сканирования A размеров M х ( m х n ).

2.    Оптимизация геометрии ВОИС

Спецификой задач волоконно-оптической томографии является наличие ультрамалоракурсной схемы сбора данных. Как правило, в таких ВОИС число измерительных линий меньше числа контролируемых областей. Имеет место недоопределённость СЛАУ (3).

В силу того, что входные данные имеют большую размерность, необходимо выполнить предобработку, позволяющую выделить наиболее значимые параметры, снизив тем самым число свободных переменных в СЛАУ (3).

В данном контексте оптимизация ВОИС заключается в удалении строк и столбцов по краям матрицы f (в «обрезке» матрицы f ), сумма элементов которых равна нулю. Зная размер матрицы f и значения столбца проекционных данных (4), всегда можно проверить, имеет ли матрица f такую строку или столбец. Затем строки и столбцы, обладающие этим свойством, удаляются из матрицы f . Далее модифицируются сама матри ца (2) и столбец проекционных данных.

В результате выполнения алгоритма «обрезки» образуется новая матрица f размера n ' × m ', причём n ' ≤ n , m ' ≤ m . Таким образом, при выполнении описанного выше алгоритма производится выделение областей-кандидатов, в которых находятся искомые «объекты».

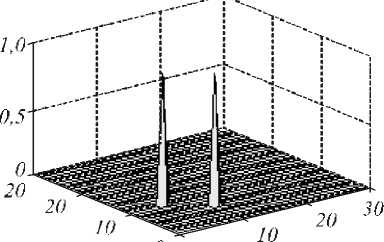
Приведём пример применения вышеизложенного метода для конкретного распределения параметра физического поля, которое в аналитической форме задаётся ф ункцией вида (рис. 2 а ).

• -0.5 ( ( x -6 ) ² + ( у -11 ) ² ) -0.5 ( ( x -16 ) ² + ( у -7 ) 2 )

z ( x , у ) = e '+ e .

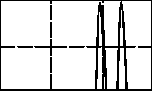
На рис. 2 представлены проекционные данные для двух взаимно перпендикулярных направлений сканирования. Из графиков видно, что первые и последние значения проекционных данных в обоих случаях имеют довольно много нулевых значений и , следовательно, целесообразно произвести процедуру предобработки в виде обрезки области по краям.

В результате применения алгоритма обрезки ВОИС исслед уемая измерительная сеть c размерами n × m = 30 × 30 преобразуется в сеть с размерами n ' × m ' = 7 × 11 (рис. 2).

После описанной выше процед уры «обрезки» области (соответственно матрицы f ) можно применять как обычные процедуры восстановления, такие как FBP[4], ART[7-8] , так и специальные, разработанные авторами, алгоритмы UQC[9-10], а также алгоритмы нейронных сетей для восстановления ис-след уемы х ф ункци й [6, 11-12].

После окончания восстановления функций для «обрезанной» области n ' х m ' производится процедура восстановления первоначальных размеров n х m с использованием списка поверхностного слоя, содержащего информацию об удалённых строках и столбцах матрицы f.

т

б)                              в)

т

г)

Рис. 2. Исследуемая функция z ( x y ) _ e -0.5(( x - 6)² + ( y - 11)²) ₊ e - 0.5(( x - 16)² + ( y - 7)²) графики проекций (б),(в), подобласть, полученная в результате применения процедур ы «обрезки» (г)

3.    Комплекс нейронных сетей

Следующим пунктом обработки данных является нейросетевая обработка проекционных данных, полученных в результате оптимизации геометрии ВОИС:

Пусть ВОИС после применения процедуры, описанной в п. 2, имеет размеры n ' х m ', n ' <  n , m' <  m . Размеры n и m , вообще говоря, должны уменьшиться ( n ' <  n , m ' <  m ). Это происходит в подавляющем большинстве случаев, т.к. пространственная частота b = п накладывает ограничения на размеры исследуемых объектов. В крайнем случае, придётся пользоваться нейронной сетью для всей области.

Заранее неизвестно, какие это будут размеры. Поэтому естественным образом возникает вопрос, какого конкретно размера нейронную сеть нужно использовать?

Ответ на поставленный вопрос содержится в подходе, предложенном в данной работе. Заключается он в следующем:

• 1.    Обучим параллельно (независимо друг от друга) несколько нейронных сетей разных р азмеров.

• 2.    Для обработки проекционных данных, поступающих от ВОИС, размера n ' х m ', n ' <  n , m ' <  m выбираем в множестве SN вида (6) нейронную сеть подходящего размера, т.е. NN ( n i , m i ), для которой

Обозначим через NN ( n i , m i ) нейронную сеть размера n i х m i , т.е. нейронную сеть, которая предназначена для обработки ВОИС соответствующего размера.

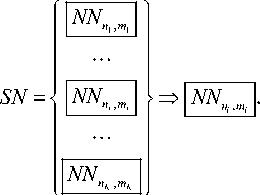
Через SN обозначим множество всех K заранее обученных нейронных сетей вида NN ( n i , m i ):

SN =

= { NN ( n i , m i ), ..., NN ( n i , m t ),..., NN ( пк , m K )}, (6) n i < ... <  n i < ... <  n_K , m 1 < ... <  m i < ... <  m_K ,

( nt , mt ) ^ ( n , m j ) при t ^ j , 1 <  t , j <  K .           (7)

n - <  n ' <  n t , m -i <  m ' <  m t , 1< t , j <  K .           (8)

Из условий (7), (8) очевидным образом следует, что нейронная сеть NN ( n t , m t ) является сетью наименьшей разм ерности, с помощью которой можно обработать проекционные данные измерительной сети размера n ' х m '.

4.    Использование RBF-сетей

В качестве нейронных с етей в работе использованы нейронные сети радиально-базисного типа. Ранее в статье [6] авторами уже была исследована возможность применения радиально-базисных нейронных сетей (RBFNN).

Формируемый сетью информационный массив, представленный вектором G, являлся набором томографических данных, по которым нейронная сеть должна реконструировать вектор F . Таким образом, нейросеть должна выполнить преобразование вида F = A^-i(G) , предварительно пройдя обучение на множестве обучающих пар {( G, F) }.

Для создания обучающей страницы использовался способ выбора обучающих пар «с подкреплением», при котором рассматривались пары вида ( G t , F t ), где AF t = G t .

При создании обучающих пар RBFNN в [6] использовались функции гауссовского типа

• ^- a . ( ( x ^- c . ) ^{2 +} ( y ^- b , )² )

z ( x , y ) = e ' ', причём параметры b _t , c _t подбирались как узлы решётки соответствующей схемы сканирования и пары Гауссиан.

Например, для поля 5х5 была составлена обучающая страница, состоящая из 3325 обучающих пар, на которой была обучена сеть RBFNN. Экспериментально было показано, что построенная сеть позволяет осуществлять восстановление функций пространственного распределения исследуемой физической величины с погрешностью в отдельной точке не более 2%, обладает хорошими прогнозирующими возможностями. Однако было отмечено, что при этом способе восстановления в задачах с применени ем ВОИС повышенных размерностей возникают серьёзные трудности при об учении сети ввиду слишком большого объёма обучающих страниц. Поэтому возникла необходимость поиска оптимальных путей при применении нейронных сетей.

Одним из способов оптимизации обработки информации является использование набора заранее обученных нейронных сетей различных размерностей.

Выбор эталонных функци й должен находиться в зависимости от ширины спектра b исслед уемой функц ии f ( x, y ). Ф ункц ии гауссовского типа

( X -ai((x — ci)2 +(У — bi f ) ZQX z (x, y) = e ' 1 (9) могут быть использованы в качестве таковых, так как они принимают ненулевые значения только в зоне вокруг определённого центра.

Для проведения анализа нейросетевого метода решения задачи с помощью RBFNN в этой работе была рассмотрена томографическая задача восстановления фун кций ФП по информации, поступающей с информационно-измерительной системы размерности 30×30.

Предполагалось, что эталонное воздействие на поле имеет вид гладкой функции с ограниченной эффективной шириной спектра b , равной условной спектральной единице п . Считается, что все значения функц ии неотрицательны и нормированы.

В данной работе использованы те же три типа эталонных распределений физической величины, что и в [6]. Первый и второй типы относятся к регулярному способу, а третий – к случайному. Опишем их подробнее.

Тип I. Эталонные распределения поля в этом случае представляют собой одиночные Гауссианы вида (9), центры которых расположены в узлах измерительной сети. Было установлено, что оптимальными для обучения являются параметры a i , принимающие значения 0 <  a i <  5 .

Тип II. Аналитически эти ф ункции могут быть представлены в виде

, - a l (⁽ x - c 1 ^{) 2 + (} У - ^Ь 1 ^{) 2} } "  a 2 (⁽ x - c 2 ^{) 2 + (} У - ^Ь 2 ^{) 2} }

z ( x, y ) = e ^{v ;} + e ^{v ;} (10) при условии, что носители находятся на расстоянии не менее 2 п /Ь . Это пары Гауссиан с непересекаю-щимися носителями.

Тип III. Эталонные распределения этого типа были получены с помощью процесса рандомизаци и с нормированием. Каждому целочисленному случайному набору a 1 , а 2, b 1 , c 1 , b 2 , c 2 = 1, N ставилась в соответствие функ ция вида (10). Каждый вектор перед включением в обучающую страницу был нормирован.

5.    Численное моделирование

Для проведения анализа нейросетевого метода решения задачи с помощью комплекса RBFNN была рассмотрена информационно-измерительная сеть 30×30.

В таблице 1 для каждой нейронной сети радиально-базисного типа, принадлежащей множеств у SN, представлены след ующие характеристики:

– размеры ( n i , m i ) соответствуют геометрии измерительной сети, которая обрабатывается нейронной сетью радиально-базисного типа NN ( n i , m i ),

– общий объём обучающей страницы (ОС) включает типы I – III ,

– среднее время обучения по результатам серии нескольких (10-15) вычислительных экспериментов,

– значения нормированной среднеквадратичной ошибки (СКО) по всей обучающей странице,

– число воздействий, распознаваемое нейронной сетью NN ( n i , m i ),

– возможности прогнозирования, т.е. распознавание сетью видов воздействий, которые не принадлежат обучающей странице,

– качество обучения является усреднённой характеристикой, связанной в том числе с наличием артефактов в результате недостаточного объёма обучающей страницы.

Из приведённых в таблице 1 результатов видно, что с ростом размера сети качество обучения падает.

В таблицах 2 и 3 представлены результаты работы предложенного метода для эталонных воздействий на измерительную сеть одиночных воздействий (9) и двойных воздействий (10), соответственно.

Из прив едённых резуль татов след ует, что обработка с помощью процедуры обрезки области с послед ующей коллектив ной обработкой нейронными сетями даёт большой в ыигрыш в точности. Это объясняется локализацией места воздействия на сеть и обработкой с помощью нейронной сети, как прав ило, меньшей размерности, которая обучена более качественно и быстро. При этом значение ошибки СКО для элементов из обучающей страницы падает в 15-20 раз.

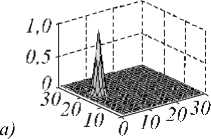
На рис. 3 показаны результаты обработки эта-

( х        -0.5 ( ( x -6 )² + ( У -19 )² )

лонного воздействия вида z ( x , y ) = e '          .

После локализации воздействия получ ена подобласть размера 3×3, которая обраб атыв ается хо рошо об ученно й нейронной сетью NN (3, 3). В завершение, были восстановлены исходные размеры области (рис. 3 б ). На рис. 3 в представлен результат восстановления исследуемой функции с помощью нейросети максимального размера NN (30, 30). Кач ество обучения NN (30, 30) невысоко е, что объясняет появление артефактов д аже при восстановлении од ного возд ействия на измерительную сеть .

Таблица 3. Результаты обработки данных комплексом RBFNN для эталонных функций вида (10)

Расстояние межд у центрами Гаусси ан	n ' × m '	Размер в %	СКО
4	3×5	1,6 %	1,9×10-4
5	4×5	2,2 %	1,87×10-4
11	7×13	10%	0,0181
20	14×14	22 %	0,0017
34	25×25	69,5 %	0,0024

Таблица 1. Характеристики нейронных сетей радиально-базисного типа, принадлежащих множеству SN

	Размер ( n i , m i )	Объём ОС	Время обучения	Ошибка mse по всей ОС	Число воздействий	Прогнозирующие свойства	Качество обучения
1	3×3	1390	5 с	2×10-27	3	+	высокое
2	5×5	3325	2 мин.	2,8×10-16	4	+	высокое
3	7×7	4850	3-4 мин.	1,3×10-27	4	+	высокое
4	10×10	8500	22 мин.	1,8×10-27	3	+	среднее
5	15×15	9102	22 мин.	3,5×10-27	3	±	среднее
6	20×20	9264	30 мин.	3,4×10-29	3	±	среднее
7	30×30	9000	25 мин.	10 -25	2	–	низкое

Таблица 2. Результаты обработки данных комплексом RBFNN для эталонных функций вида (9)

	a i	n ' × m '	Размер в %	Время обработки, с	Ошибка СКО
1	0,5	3×3	1 %	0,0554	1,9×10-4
2	0,1	5×5	2,77 %	0,0823	0,0062
3	0,05	7×7	5,44 %	0,0879	0,0102

б)

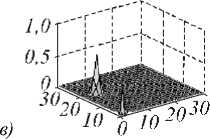
Рис. 3. Исследуемая функция z(x,y)= e (( ) (у )) (а), результат восстановления с применением комплекса нейронных сетей SN (б), результат восстановления с помощью NN (30, 30) (в)

Заключение

В статье представлен новый комбинированный алгоритм обработки проекционных данных для восстановления информации, поступающей с волоконно-оптических измерительных линий распределённой ВОИС.

Этот алгоритм заключается в последовательном выполнении двух алгоритмов:

• 1)    в предобработке измерительной информации с помощью локализации мест воздействия на ВОИС,

• 2)    в применении комплекса нейронных сетей для обработки измерительных систем различной геометрии.

Из приведённы х результатов след ует, что

• 1)    обработка с помощью процедуры обрезки области с послед ующей коллективной обработкой нейронными сетями даёт выигрыш в точности во многом за счёт локализации места воздействия на сеть и обработки с помощью нейронной сети, как правило, меньшей размерности, которая обучена более качественно и быстро; при этом значение ошибки СКО для элементов из обучающей страницы падает в 15-20 раз;

• 2)    уменьшение ошибки СКО и сокращение времени обработки главным образом зависят от того, насколько радикально был оптимизирован вычислительный процесс в результате предобработки и от сложности восстанавливаемой ф ункц ии.