Обработка изображений векторных полей с применением линейной интегральной свертки
Автор: Ворожцов Евгений Васильевич
Журнал: Проблемы информатики @problem-info
Рубрика: Средства и системы обработки и анализа данных
Статья в выпуске: 1 (5), 2010 года.
Бесплатный доступ
Обсуждаются недостатки таких известных способов получения линий тока из векторных полей, как исполь- зование функций тока и интегрирование дифференциальных уравнений, справедливых вдоль линий тока. Описывается сравнительно новый метод визуализации линий тока − метод линейной интегральной свертки, который вытекает из заданного в цифровой форме векторного поля и существенно использует алгоритмы цифровой обработки изображений. Показано, что метод реализуется в три этапа: генерация изображения типа "белый шум" во всей области; сглаживание данного изображения вдоль линий тока на основе заданно- го векторного поля; улучшение полученного сглаженного цифрового изображения, для чего, в частности, предлагается использовать морфологическую операцию утончения сегментов линий тока. Дается количест- венная оценка точности метода линейной интегральной свертки с применением нескольких критериев. Приводятся некоторые результаты вычислительных экспериментов на двумерных векторных полях, точные линии тока которых известны. Показано, что метод линейной интегральной свертки является достаточно общим и универсальным и не требует для своей реализации какой-либо априорной информации об иссле- дуемом явлении.
Научная визуализация, векторные поля, линии тока, цифровые фильтры, линейная интегральная свертка, гидродинамика
Короткий адрес: https://sciup.org/14320013
IDR: 14320013 | УДК: 004.932:532.5
Текст научной статьи Обработка изображений векторных полей с применением линейной интегральной свертки
Введение. Научные исследования разнообразных динамических процессов часто связаны с необходимостью детального анализа этих процессов на основе имеющихся векторных полей. В свою очередь, этот анализ опирается на детальное изучение линий тока, получаемых из векторных полей. При этом к алгоритмам компьютерной визуализации линий тока предъявляются требования точности, скорости и высокой детальности картины линий тока [1].
Одним из известных способов построения линий тока по заданному векторному полю является численное интегрирование обыкновенных дифференциальных уравнений вдоль линии тока:
dx/dt = u, dy/dt = v, dz/dt = w ,
где x,y,z - декартовы прямоугольные координаты точки в исследуемой пространственной области; t - параметр вдоль линии тока; u,v,w - проекции вектора скорости среды на оси координат Ox, Oy, Oz . Известен также способ построения линий тока как линий уровня функции тока. Оба эти способа построения линий тока реализованы в системе инженерных и научных расчетов MATLAB. Выбор данного пакета программ в настоящей работе обусловлен тем, что в его составе имеется пакет прикладных программ "Image processing toolbox", который включает более 100 функций, реализующих наиболее распространенные методы и алгоритмы обработки цифровых изображений [2]. В системе MATLAB имеется встроенная функция streamline(X,Y,Z,U,V,W, startx, starty, startz) , в которой численно интегрируются либо три уравнения (1), либо, в случае линий тока на плоскости, какие-либо два уравнения системы (1). Массивы X, Y, Z определяют координаты для U, V, W; startx, starty и startz определяют стартовые положения линий тока. Основная трудность при использовании функции streamline(…) связана с выбором начальных точек линий тока. При неудачном выборе этих точек можно не заметить (пропустить) некоторые важные особенности изучаемого векторного поля, такие как области завихрения или рециркуляции, линии растекания, критические точки и т. п.
Известный способ построения линий тока как линий уровня функции тока имеет существенное ограничение: он применим только к двумерным векторным полям. Когда число пространственных переменных равно трем, функцию тока удается построить лишь в нескольких частных случаях [3].
-
2. Метод LIC. Рассмотрим метод LIC ("line integral convolution" – линейная интегральная свертка).
-
2.1. Описание метода. Метод LIC, предложенный в работе [1], вызвал большой интерес различных исследователей, нуждающихся в картинах линий тока. Достоинства LIC-метода оказались столь значительными, что в настоящее время в мире насчитываются тысячи научных работ, в которых либо LIC-метод применяется в прикладных задачах, либо предлагаются его модификации.
-
В экспериментальной аэродинамике широко известен метод нанесения пленки из смеси масла и краски (или сажи) на поверхность обтекаемого тела. Когда поток газа обдувает поверхность тела, смесь масла и краски преобразуется в линии тока на поверхности. Данный способ визуализации течения наиболее эффективен при наблюдении отрывов потока газа и его повторных присоединений [4]. Однако следует отметить наличие элементов случайности:
-
1) так как указанная смесь наносится на поверхность вручную, толщина ее пленки различна на разных участках поверхности;
-
2) на наклонных участках поверхности толщина пленки меняется еще и под действием силы тяжести (пленка стекает);
-
3) на различных участках пленки локальная концентрация сажи в масле также неодинакова.
Тем не менее метод масляно-сажевой пленки позволяет получать очень информативные картины линий тока на поверхностях обтекаемых тел (см., например, работу [5]).
Метод LIC включает следующие основные этапы:
-
- генерация цифрового изображения типа "белый шум" во всей пространственной области;
-
- сглаживание данного изображения вдоль линий тока на основе заданного поля скоростей;
-
- улучшение полученного сглаженного изображения: контрастирование, выравнивание гистограммы яркостей и т. п.
Разработанная головная "MATLAB"-программа, реализующая LIC-метод, имеет имя StreamLIC.m . В этой программе метод LIC реализован для случая двух пространственных переменных: LIC-изображения линий тока строятся в сечении y = const, т. е. действующими пространственными переменными являются переменные x и z .
Для улучшения качества итогового LIC-изображения сначала осуществлялась интерполяция исходного поля скоростей ( u,w ) на более мелкую равномерную пространственную сетку в плоскости ( x, z ). Это небходимо для того, чтобы не потерять информацию о мелких деталях векторного поля в областях сгущения исходной сетки [6].
Построение мелкой сетки выполнялось по формуле hf = min(h1, h3)/fmagn,
где h 1 , h 3 - среднеарифметические значения шагов исходной неравномерной сетки вдоль осей x и z , соответственно; f magn - задаваемый пользователем коэффициент увеличения детальности сетки при измельчении исходной сетки, f magn ^ 1. Реальное ограничение сверху на f magn диктуется лишь быстродействием используемого компьютера. При этом чем детальнее исходная пространственная сетка, тем меньшее значение f magn можно брать. Заметим, что машинное время, необходимое для получения LIC-изображения, пропорционально величине f m 2 agn .
Формула (2) показывает, что новая, более мелкая сетка состоит из квадратных ячеек, длина стороны ячейки равна h f . Таково требование исходного LIC-метода. Для того чтобы ослабить данное требование и рассматривать ячейки мелкой сетки с неравными сторонами, требуется довольно существенная переработка программы StreamLIC.m . Однако в этом нет необходимости. Следует отметить, что в работах [7, 8] LIC-метод обобщен на случай криволинейной пространственной расчетной сетки.
Величины u, w интерполировались из центров исходных ячеек в центры ячеек более мелкой квадратной сетки с помощью встроенной "MATLAB"-функции interp2(x,z,U,xf,zf,‘linear’) , где U - одна из величин u, w ; (x,z) - координаты точек исходной сетки, в которых заданы значения U ; (xf,zf) - координаты центров ячеек более мелкой сетки; при задании аргумента ‘linear’ реализуется билинейная интерполяция, при задании аргумента ‘cubic’ - бикубическая сплайн-интерполяция.
Обозначим через Wik числовое значение "белого шума", генерируемого в центре ячейки мелкой сетки. "Белый шум" { Wik } генерировался по формуле Wik = randn ( N 3 f ,N 1 f ) ( randn - "MATLAB"-функция, формирующая массив размера N 3 f ×N 1 f , элементами которого являются случайные величины, распределенные по нормальному закону с математическим ожиданием 0 и среднеквадратичным отклонением 1; N 1 f , N 3 f - числа ячеек мелкой сетки в направлениях осей x и z соответственно). Элемент случайности, присутствующий в алгоритме LIC-метода – единственный элемент, который является общим для LIC-метода и масло-сажевого метода из экспериментальной аэродинамики. Однако метод линейной интегральной свертки имеет существенное преимущество по сравнению с масло-сажевым методом. LIC-метод позволяет определять линии тока не только на поверхностях обтекаемых тел, но и в пространстве между телами, заполненном движущейся средой.
В дальнейших вычислениях с использованием LIC-метода осуществлялось деление длины сторон мелкой сетки на величину h f , для того чтобы получить квадратные ячейки со стороной, равной единице.
Для улучшения "белого шума" в работе [1] применялась дополнительная фильтрация нижних частот с помощью фильтра "Butterworth" четвертого порядка с частотами обрезания 128, 84, 64 и 32. Подробное описание указанного фильтра приведено в [2, 9]. В разработанной программе StreamLIC.m применение фильтра "Butterworth" считалось нецелесообразным по следующим причинам:
-
- численная реализация этого сглаживающего фильтра требует дополнительных расходов машинного времени;
-
- с уменьшением частоты обрезания "белый шум" становится более размытым, что ухудшает качество LIC-изображения (см. рис. 6 в работе [1]).
Локальное поведение векторного поля можно аппроксимировать, вычисляя локальную линию тока, начинающуюся в центре ячейки (i, k) мелкой сетки. Пусть P0 - стартовая точка линии тока, P0 = (xik, zik). Адвекция точки P0 вдоль линии тока вычисляется по формулам xm = xm-1 + Ax m-p
z m = z m -1 + A z m -1 , m = 1,2,--- -
Алгоритм вычисления приращений координат A xm - 1 , A zm - 1 при движении вдоль линии тока со скоростью v = ( u, w ) сводится к рассмотрению следующих восьми случаев.
Случай 1 . Пусть ( im - 1 , km_ 1 ) - центр ячейки, в которой находится точка Pm - 1 , пусть также
-
u, к > 0, w, к > 0, ( w / u )i к - 1,
i m - 1 , k m - 1 i m - 1 , k m - 1 x 7 im - 1 , k m - 1
т- е. вектор скорости, выходящий из центра ячейки ( im - 1 , km - 1 ), пересекает правую сторону ячейки ( im - 1 , km - 1 ), (рис. 1, а ). Тогда, проведя элементарное геометрическое вычисление, получаем:
A x m -1 = 0,5, A z m -1 =A x m -1 ( w / u ),
' ' im - 1 , km
б
а
в
г
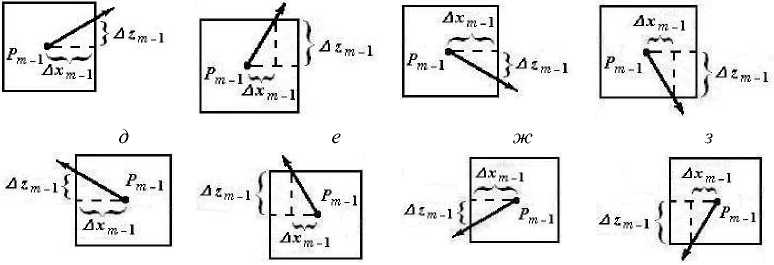
Рис. 1. Случаи расположения вектора скорости относительно сторон ячейки
Случай 2. Пусть и, . > 0, w . > 0, но ( w / и ) . > 1 (рис. 1, б). Тогда "' im - 1 , k m - 1 i m - 1 , k m - 1 i m - 1 , k m - 1
A z m -1 = 0,5 A x,
= A z m -1 / ( w / u X . , m - 1 , m - 1
.
Случай 3 .
u
' m - 1 , m - 1
i , k.
' m - 1 , m - 1
< 0,
|( w / и ) , | < 1 (рис. 1, в ). Тогда i m - 1 , k m - 1
A x m -1 = 0,5 A z m -1 = A x m -1 ( w / и к - 1 , k m - 1 < 0
Случай 4 .
u
1 m - 1 1 m - 1
i m - 1 , k m - 1
< 0,
|( w / и ) , | > 1 (рис. 1, г ). Тогда i m - 1 , k m - 1
A z m -1 = 0,5, A x,
= A z m -1 / ( w / u X . , > °.
i m - 1 ’^ m - 1
Случай 5 .
u im-1, km-1
i m - 1 , k m - 1
> 0,
|(w/и) |< 1 (рис. 1,д). Тогда im-1, km-1
A x,
= A x m -1 ( w / u \ k > 0 m - 1 , m - 1
Случай 6 .
u
' m - 1 , m - 1
i , k.
' m - 1 , m - 1
|( w / и ), , | > 1 (рис. 1, е ). Тогда i m - 1 , k m - 1
A z m -1 = 0,5, A x,
= Azm-1/ (w / u X . , > 0
i m - 1 ’^ m - 1
Случай 7 .
u im-1, km-1
i m - 1 , k m - 1
< 0, |( w / и ) , | < 1 (рис. 1, ж ). Тогда i m - 1 , k m - 1
A x m -1 =- 0,5, A z m -1 = A x m -1 ( w / u ) k < 0 m - 1 , m - 1
Случай 8 .
u
' m - 1 , m - 1
i , k.
' m - 1 , m - 1
< 0, |( w / и ) , | > 1 (рис. 1, з ). Тогда i m - 1 , k m - 1
A z
-0,5, Ахт-1 =Azm-1/ (w / u )
i m - 1 , k m - 1
Сравнивая случаи 1, 3, 5, 7, нетрудно заметить, что соответствующие формулы для вычисления приращений A xm - i и A zm _ ! можно объединить в следующие две формулы:
Axm-1 = 0,5 Sign( и k X Az m -1 =Ax m -1 (w / и),- k .
m 1 m 1 m - 1 , m - 1
Аналогичным образом сравнивая случаи 2, 4, 6, 8, эти случаи также можно объединить в две формулы
Az m-1 = 0,5 Sign( wimvkm J; Axm-1 =Az m -J ( w / и ) , . ■ m-1, m-1 im-1,km-1
Вычислив приращения A xm - 1 и A zm - 1 по одной из формул (4), (5), по формулам (3) легко найти координаты xm , zm следующей точки Pm . Однако при этом важно обеспечить, чтобы точка Pm вошла в соседнюю ячейку сетки [1]. Для этого в соответствии с [1] в формулах (4), (5) вместо множителя 0,5 использовался множитель £ 1 = 0,5(1 + £ )
( е - малое положительное число; в приведенных ниже примерах расчетов значение £ = 10 — 6 ). Итак, формулы для вычисления A xm - 1 и A zm - 1 имеют окончательный вид
- если |( w / и ), | < 1, то
4 ' im - 1 , k m - 1
) A z m -1 = A x m -1 ( w / u ), , m -1 ' ' im - 1 , k m - 1
А х„ , = е sign( u, t m - 1 la V i m - 1 , k m
- если |( w / и ), , | > 1, то
4 y im - 1 , k m - 1
Azm-1 = £1 Sign(w. „k. , ) Axm-1 = Azm-1 / ( w / u ), m 1, m1 im-1 ,*vm
Локальная линия тока продолжается из центра ячейки и в отрицательном направлении, т. е. с компонентами (- u ,- w ). Это обеспечивает симметрию линии тока относительно центра ячейки. Для того чтобы найти соответствующие приращения A x m -1 , A z m -1 , в формулы (6), (7) подставлялось значение - и вместо и и значение - w вместо w .
Теперь подсчитываются соответствующие длины дуг локальной линии тока:
A s m -, = ( A x m -, + A z m -, f , A s m -, = ( A x m - + A z m - ) 0,5 .
Сглаживание значения яркости изображения в ячейке ( i, k ) мелкой сетки осуществляется по формуле LIC-метода:
S
ik
ll
S Wm,kmhm Wmkmhm m=0______________m=0___________ ll'
S hm + S hm m=0
где sm-1 + As m-1
J k ( w ) dw , s m - 1
p sVi+AsL_i hm = J, k (w) dw,
J s m - 1
s 0 = 0, s m = s m - i + A s m - i . Величина l в соотношении (8) равна такому значению i , при котором s i < L < s i + i , ( L - длина локальной линии тока, задаваемая в терминах единичной длины стороны ячейки мелкой сетки). В работе [1] обсуждалось оптимальное значение параметра L, которое должно задаваться пользователем. С учетом рекомендаций [1] определено, что с точки зрения качества LIC-изображения оптимальными являются значения L в интервале 4 < L < 10. Следует отметить, что при расчете выходного сигнала Sik по формуле (8) суммарный расход времени пропорционален L 2.
Функция k(w) в (9) - это ядро свертки. В работе [1] приводились аргументы в пользу применения функции k(w) вида k (w) =
1 + cos( cw ) 1 + cos( dw + в )
Здесь первый множитель (1/2)(1 + cos( cw )) соответствует ядру, применяемому в фильтре Hanning, обсуждение которого приведено, например, в работе [9]. Множитель (1/2)(1 + cos( dw + в )) - это функция ряби (ripple function); c и d - константы наращивания (dilation), в - сдвиг по фазе функции ряби, задаваемый в радианах.
Вследствие простоты ядра k ( w ) (10), интегралы в (9) легко вычисляются в аналитическом виде
J k ( w ) dw = ! [ b - a + sinc bc l-sinf ac ) a
sin( bd +в ) - sin( ad +в )т
+ d ] +
1 sin b ( c - d ) - в J - sin [ + 4[ 2( c - d )
sin b ( c + d ) + в } - sin a ( c + d ) + в } 2( c + d )
Из (11) следует, что необходимо задавать различные значения c и d, чтобы избежать обращения знаменателя в нуль.
Множители (1/2)(1 + cos( cw )) и (1/2)(1 + cos( dw + в )) имеют периоды T 1 = 2 п /c и T 2 = 2 п /d соответственно, т. е. периоды зависят от констант c,d . Если в функции ряби задавать низкую частоту (т. е. малые значения d ), то с изменением сдвига по фазе в эта функция будет существенно меняться. Это проявляется в LIC-изображении как периодическое размывание и укручение (от англ. steepening – увеличение крутизны профиля) профилей яркости. Использование в функции ряби более высокой частоты приводит к оконному фильтру с почти постоянной выходной частотой, так как общая форма фильтра меняется незначительно. Но тогда отрезки линий тока будут более короткими. Если частота ряби превосходит предел Найквиста [9], определяемый размером пикселя, то длины отрезков линий тока становятся равными нулю. Как указывалось в [1], за счет увеличения пространственного разрешения (увеличения знаменателя f magn в формуле (2)) всегда можно добиться и оптимальной выходной частоты, и увеличения длин сегментов линий тока, но это, как отмечалось выше, приводит к увеличению объема вычислений, необходимых для получения LIC-изображения.
Очевидно, что оптимальный подбор констант c , d , в для каждого исследуемого течения дает дополнительные возможности для улучшения качества линий тока, генерируемых по LIC-методу.
Полученное по формуле (8) LIC-изображение S = { Sik } может непосредственно использоваться для визуализации линий тока. Однако имеются возможности для дальнейшего улучшения качества LIC-изображения, предложенные в работах [6-8]. В программе StreamLIC.m реализованы два способа улучшения LIC-изображения, предложенные в [6].
Первый способ состоит в том, чтобы использовать LIC-изображение S в качестве исходного для следующей итерации по LIC-методу. Иными словами, на второй итерации вместо исходного "белого шума" W в формуле (8) используется LIC-изображение S . В результате получаются линии тока, которые различаются в большей степени, чем при выполнении лишь одной итерации по LIC-методу. Как указывалось в [6], дальнейшие итерации (третья и т. д.) не приводят к значительным различиям в результатах по сравнению со случаем, когда LIC-алгоритм выполняется дважды. Кроме того, суммарное потребляемое машинное время прямо пропорционально числу итераций по LIC-методу. Поэтому рекомендуется выполнять не более двух итераций.
Другой способ улучшения LIC-изображения, предложенный в работе [6], заключается в приближенном выравнивании гистограммы яркости исходного "белого шума". Фильтр выравнивания гистограммы яркости сдвигает значения Wik к крайним значениям диапазона. Для приближенного выравнивания гистограммы в [6] предлагалось перевычислять значения Wik по формуле а W >0
w _ ) W k ’ W ik > 0, W' i
-
I- W k Г , W k < 0 .
В (12) величина а задается пользователем; в работе [6] для а рекомендован диапазон 5 < a < 7.
Так как вычисления по формуле (8) - это операция сглаживания исходного LIC-изображения, то в результате происходит потеря контрастности получаемого изображения. В работе [10] предлагалось применять контрастирование LIC-изображения по формуле е, _ % (s.t +1)5 Sik = Sik ,
где Sik - изображение, получаемое отображением LIC-изображения Sik на интервал [0,1]. Заметим, что если
0 < Sik < 1, то показатель степени в (13) варьируется от 1/8 до 4.
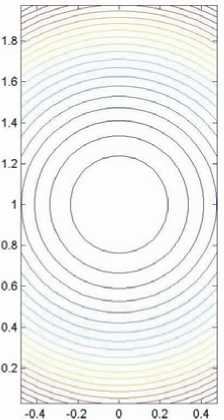
Теперь приведем некоторые результаты численных экспериментов с использованием LIC-метода для течения среды с круглым вихрем, функция тока которого имеет вид у (x,z) = (1/2) [(x -Xc)2 + (z - Zc)2]
( Xc, Zc ) - координаты центра вихря). Тогда с помощью формул u = ду / д z, w = -д^ / д x находим: u ( x,z ) = z - Zc , w ( x,z ) = - ( x - Xc ). Вектор вихря скорости rot v = (0, 2, 0) имеет лишь одну ненулевую компоненту, так что |rot v | = 2.
а
б
в
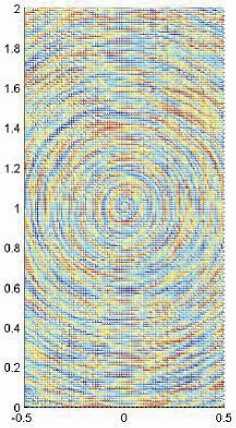
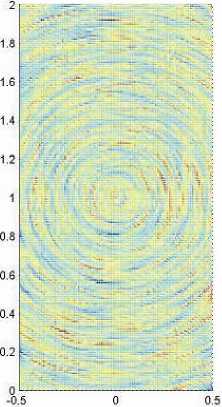
Рис. 2. Линии тока круглого вихря:
а - линии тока, полученные как линии уровня функции тока y (x,z); б - LIC-изображение 1W, цвет C = 1W; в - LIC-изображение 1W, цвет C вычислен по формуле (15) при у = 0,5
На рис. 2, а показаны линии тока рассматриваемого течения, полученные как линии уровня функции тока (14) с помощью MATLAB-функции contour.m . Видно, что линии тока - концентрические окружности с центром в точке ( X c ,Z c ).
Следуя работе [9], обозначим через lW результат однократного применения метода LIC к "белому шуму" W , через llW = lS - результат двукратного применения метода LIC. В примерах расчетов по LIC-методу, приведенных на рис. 2, б , в , в соотношении (10) использовались значения d = 0,1, в = 0,15. Для того чтобы выполнялось неравенство c ^ d , было выбрано значение c = 0,05. Это позволяло получить LIC-изображения, сопоставимые по качеству (прежде всего, по длинам сегментов линий тока, ухватываемым LIC-методом) с приведенными в работе [1]. На рис. 2, б показано цветное LIC-изображение lW , полученное при вызове MATLAB-функции mesh(xx,zz, lW ) , где окраска пропорциональна высоте поверхности lW . Если в список параметров функции mesh ввести четвертый параметр C , управляющий локальным цветом, то можно усилить цветовое различие между соседними линиями тока на LIC-изображении. С помощью нескольких численных экспериментов эмпирически было найдено, что задание цвета по формуле
C ik
S Y k , S ik > 0,
-I S ik Г , S ik ^ 0
с показателем у = 1/ a приводит к существенному усилению цветового контраста LIC-изображения S = 1W (ср. рис. 2, б и 2, в ). Автором настоящей работы проводились вычислительные эксперименты, в которых не применялось приближенное выравнивание гистограммы по формуле (12), тем не менее выполнялась операция вычисления цвета согласно (15). В таких случаях целесообразность операции (15) вытекает из того, что положительную постоянную у можно подобрать эмпирически из требования повышения контраста итогового LIC-изображения.
В случаях, показанных на рис. 2, б, в , в (8) использовалось значение L = 10 длины окна осреднения как в положительном, так и в отрицательном направлениях вектора скорости. В формуле (2) при переходе к более мелкой сетке коэффициент увеличения f magn = 5. Это означает, что на исходной сетке окно сглаживания имело сравнительно небольшой размер примерно 4×4 ячейки.
На рис. 3, а показано LIC-изображение, полученное в результате двукратного применения LIC-метода. Сравнивая рис. 3, а и рис. 2, в , видим, что повторное применение LIC приводит к улучшению связности сегментов линий тока; иными словами, средняя длина указанных сегментов увеличилась.
а
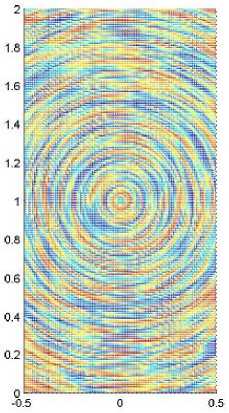
Рис. 3. Линии тока круглого вихря, полученные LIC-методом:
а - LIC-изображение llW, цвет C вычислен по (15) при у = 0,5; б - LIC-изображение lleW при а = 5, у = 0,2
б
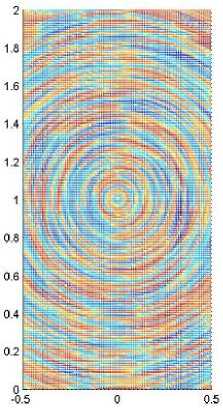
Пусть, как и в работе [6], e - оператор приближенного выравнивания гистограммы яркости по формуле (12). На рис. 3, б показано LIC-изображение, полученное в результате предварительного выравнивания гистограммы "белого шума" и последующего двукратного применения метода LIC.
Поскольку во многих профильных журналах цветные рисунки не публикуются, целесообразно рассмотреть возможность инвертирования цветного LIC-изображения в черно-белую форму. Данная операция осуществлялась в два этапа. На первом этапе LIC-изображение S отображалось на интервал яркостей [0, 1] по формуле 5' = aS + b, где a = 1,0/(Smax – Smin), b = – aSmin, Smax = maxS , Smin = minS . i,k i,k
На втором этапе черно-белое LIC-изображение генерировалось путем вызова MATLAB-функции B=im2bw( S', th), где th - заданное значение порога, 0 < th < 1; B - получаемое бинарное изображение. Чем выше значение порога, тем больше черных пикселей в черно-белом LIC-изображении, поскольку функция im2bw.m полагает значение яркости изображения в ячейке (i, к) равным нулю (черный цвет), если S'ik < th. Эта операция называется бинари- зацией по порогу. В разработанных автором MATLAB-программах LICTest.m и StreamLIC.m наряду с генерацией цветного LIC-изображения осуществляется также бинаризация. На рис. 4 приведены результаты бинаризации двух различных LIC-изображений с различными значениями порога th.
На бинарных изображениях линии тока показаны только двумя цветами (черным и белым) вместо большого количества цветов в цветных изображениях, приведенных на рис. 2, 3. На рис. 4 видно, что толщины линий тока переменные вдоль линий тока. Этого можно избежать, применяя морфологическую операцию утончения объектов на бинарном изображении. При этом сегментами линий тока будем считать те связные области, значения пикселей которых равны единице (белый цвет), а области изображения, значения пикселей которых равны нулю, будем
а
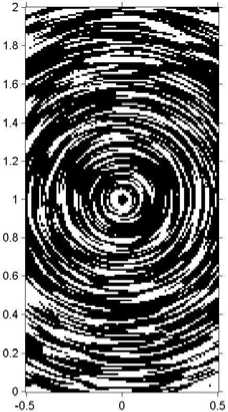
Рис. 4. Черно-белые картины линий тока, полученные бинаризацией LIC-изображений l 2 W : th = 0,53 ( а ) и l 2 eW , th = 0,56 ( б )
б в
0.5 0 0.5 0.5 0 0.5
г

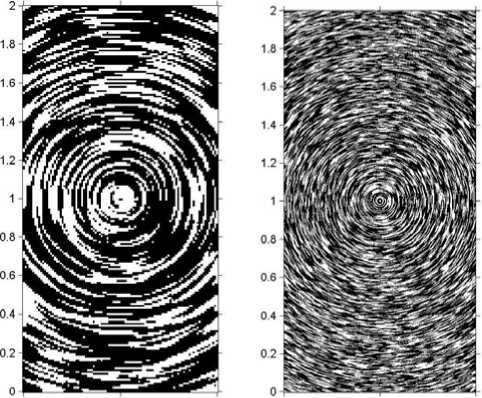
Рис. 5. Применение морфологической операции утончения: а - изображение bl 2 W ; б - изображение itbl 2 W
считать фоном. Операция B t = bwmorph(B,’thin’) выполняет эрозию объекта с учетом ряда условий для сохранения 8-связности участков остова [2, 11]. В результате сегменты линий тока, имевшие переменную толщину, превращаются в сегменты линий толщиной в один пиксель.
Обозначим через b оператор бинаризации изображения с помощью функции im2bw.m , через t - оператор морфологического утончения объектов в бинарном изображении. На изображении tbl 2 W линии тока показаны белым цветом на черном фоне. Так как обычно линии тока изображаются черным цветом на белом фоне, можно осуществить операцию инвертирования изображения, при которой белые пиксели становятся черными, а черные - белыми. Обозначим этот оператор инвертирования символом i , т. е. itbl 2 W = 1 – tbl 2 W . На рис. 5, а показано исходное бинарное изображение bl 2 W , f magn =20 в (2), размер изображения 390×780 пикселей. На рис. 5, б видно, что подавляющее большинство сегментов линий тока
а
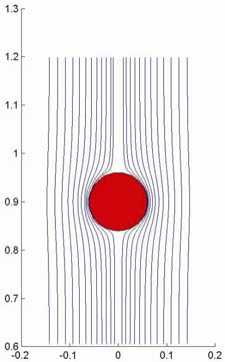
Рис. 6. Линии тока в задаче об обтекании сферы: а - линии тока, полученные с помощью функции streamline(…); б - LIC-изображение l2W, цвет C вычислен по (15) при γ = 0,5
б
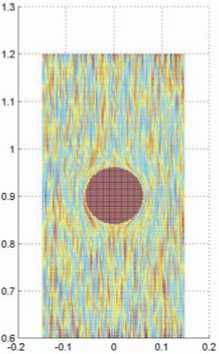
теперь имеет толщину в один пиксель.
На рис. 6, а показаны линии тока, полученные с помощью MATLAB-функции streamline(…) для задачи о безвихревом обтекании сферы потоком идеальной несжимаемой жидкости. В сечении y = 0, проходящем через центр сферы, значения составляющих скорости u,w задавались в центрах ячеек равномерной сетки в соответствии с точным решением [1]. Результат применения LIC-метода, приведенный на рис. 6, б , получен при следующих константах в (10): d = 0,05, c = 2 d , β = 3 d . В (8) использовалось значение L = 10 длины окна осреднения как в положительном, так и в отрицательном направлениях вектора скорости.
-
2.2. Точность LIC-метода. В работе [10] осуществлена сравнительная количественная оценка шести методов визуализации линий тока включая метод LIC на основе векторных полей. Было сгенерировано 500 векторных полей с различным количеством критических точек различных типов (например, точек типа седла, притягивающего узла и т. д.). Реализованы следующие количественные критерии оценки точности различных алгоритмов построения линий тока.
-
1. Определение количества критических точек в векторном поле и вычисление на этой основе процентной доли количества векторных полей (из 500 полей), в которых конкретный метод дал неправильное количество критических точек. По данному критерию LIC-метод оказался наиболее точным из шести рассмотренных методов.
-
2. Определение типов выявленных критических точек. Здесь LIC-метод по точности оказался на третьем месте
-
3. Определение средней ошибки локализации критической точки на основе изображения линий тока, построенного одним из шести методов. Положение критической точки определялось пользователем визуально на экране монитора компьютера и сразу заносилось компьютером в память, где хранились и точные координаты соответствующих критических точек. После этого вычислялась абсолютная ошибка в определении положения критической точки. В результате установлено, что метод LIC обеспечивает наиболее высокую точность определения положения критических точек по сравнению с остальными пятью методами.
-
4. Определение средней абсолютной угловой ошибки в направлении касательной к линии тока вблизи места ее вхождения в критическую точку. В этом случае метод LIC уступил по точности остальным пяти методам: указанная ошибка для LIC превышала 10о, в то время как для наилучшего по точности метода она лежала в интервале 0,5–1,0 о.
среди шести методов.
В дополнение к описанным выше количественным критериям оценки методов визуализации линий тока на примере круглого вихря было проведено исследование влияния измельчения сетки, т. е. коэффициента fmagn в (2), на точность определения локальных углов наклона касательных к линиям тока в LIC-изображении tbl2W. Пусть tbl2W = {bk,i}, k = 1,…, N3f, i = 1,…, N1f. В пределах окна изображения размером 3×3 с центром в пикселе bk,i сегмент линии тока аппроксимируется прямолинейным отрезком, описываемым уравнением z = a0 + a1x. Тогда угол ak,i между этим отрезком и положительным направлением оси x находится из уравнения tg ak,i = (dz/dx)k,i = a 1. В соответствии с методом наименьших квадратов составляется функция
F(a 0, a 1) = 'LPm (a 0 + a 1 xm - zm )\ m=1
где ( xm,zm ) - координаты всех белых пикселей в пределах рассматриваемого окна изображения; pm - заданные положительные весовые параметры (в описываемых ниже расчетах использовались значения pm = 1 V m ). Из условий экстремума д F / д а 0 = 0, д F / д a 1 = 0 легко найти выражения для a 0 и a 1 , в частности a 1 = ( S 0 S 3 - S 1 S 2)/( S 0 S 4 - S 1 2), где
S 0 = 'NPm , S1 ='LPmxm , S 2 = Р mzm , S 3 ^Pmxmzm , S 4 = NPmxm- m =1 m =1 m=1 m =1 m=1
Вычисления по методу наименьших квадратов выполнялись только в тех окнах размером 3×3, в которых количество N белых пикселей удовлетворяло неравенствам 2 < N < 6. Пусть a^i. - точный угол наклона касательной к линии тока; в случае задачи о круглом вихре akX = arctg[-(x^ - Xc)/(z^. - Zc) ].
С целью уменьшения величины | a k ,i - a “ | выполнялись также следующие операции: если a < 0, то a = a + 2 л .
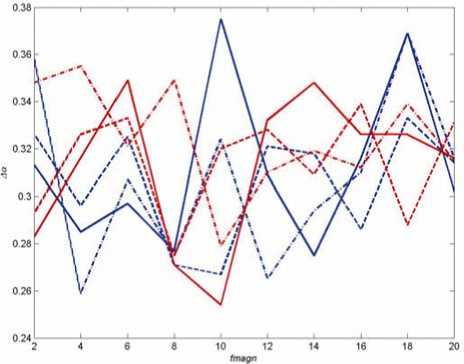
Далее, если ak,i< 1,6л(4,7< a™ <6,29), то a^i. =2п- a™ , если 4,7 После этой коррекции углов ak,i и a™. среднеквадратичная угловая ошибка Aa находилась по формуле Ka = Ns 2 (1/ Ns )X(ak,.- akD m =1 0,5 , где Ns - количество точек линий тока в LIC-изображении tbl2W, в которых вычислялись величины ak,i и a™ . На рис. 7 показана поверхность Aa = Aa(x, z) (углы измеряются в радианах) для случая изображения tbl2W, инвертированный вариант которого показан на рис. 5,б. Видно, что локальные погрешности Aa выше в следующих секто рах углов a: -п/4 < a < п/4, 3п/4 < a < 5п/4. На рис. 8 синим и красным цветом показаны линии Aa = Aa(fmagn) Рис. 7. Поверхность Aa = Aa(x, z) для случаев применения соответственно билинейной интерполяции и бикубической сплайн-интерполяции при переходе от исходной сетки к более мелкой квадратной сетке. Поскольку "белый шум" W меняется при каждом запуске MATLAB-программы генерации LIC-изображения, на рис. 8 показаны результаты первого, второго и третьего запусков программы при фиксированном значении fmagn. На рис. 8 видно, что при использовании бикубической сплайн-интерполяции абсолютный максимум погрешности (16) ниже, чем в случае билинейной интерполяции. Отсюда следует предпочтительность использования бикубической сплайн-интерполяции при формировании LIC-изображений. Конечно, этот метод интерполяции требует больших затрат машинного времени, чем билинейная интерполяция, но это время меньше времени, необходимого для вычислений по формулам LIC-метода. Необходимо также отметить, что при увеличении fmagn погрешность Δα не уменьшается. Важно отметить следующее достоинство LIC-метода: поскольку вычисления по формуле (8) проводятся в каждой ячейке независимо от других, то метод LIC весьма удобен для распараллеливания (см. также [1]). Заключение. Метод линейной интегральной свертки является универсальным методом построения линий тока по заданным локальным векторам скорости. Реализация метода проста. В отличие от известного метода интегрирования обыкновенных дифференциальных уравнений вдоль линии тока LIC-метод не требует задания начальных координат точек линий тока, иными словами, не требует ника- Рис. 8. Ошибка Δα = Δα(fmagn): синий цвет - билинейная интерполяция, красный -бикубическая сплайн-интерполяция, сплошные линии - первый запуск MATLAB-программы, штриховые -второй запуск, штрихпунктирные линии - третий запуск кой априорной информации об исследуемом течении. Поскольку в методе LIC сканируются все ячейки пространственной сетки, с его помощью можно успешно выявлять разнообразные локальные и нелокальные нетривиальные особенности векторного поля, некоторые из которых перечислены во введении. Вместе с тем имеется проблема сходимости метода при измельчении сетки.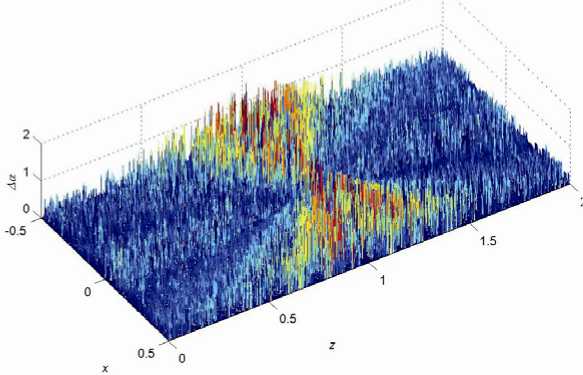
Список литературы Обработка изображений векторных полей с применением линейной интегральной свертки
- CABRAL B., LEEDOM L. Imaging vector fields using line integral convolution//Proc. of the SIGGRAPH'93 (Special Interest Group on Computer Graphics and Interactive Techniques), Anaheim (USA), 1-6 Aug. 1993. N.Y.: ACM Press, 1993. P. 263-270.
- РУДАКОВ П. И. Обработка сигналов и изображений. MATLAB 5.x./П. И. Рудаков, В. И. Сафонов. М.: Диалог-МИФИ, 2000.
- ЛОЙЦЯНСКИЙ Л. Г. Механика жидкости и газа. М.: Дрофа, 2003.
- MERZKIRCH W. Flow Visualization. N.Y.: Acad. Press, 1987.
- ЖЕЛТОВОДОВ А. А., МАКСИМОВ А. И., ШЕВЧЕНКО А. М. Топология пространственного отрыва в условиях симметричного взаимодействия пересекающихся скачков уплотнения и волн разрежения с турбулентным пограничным слоем//Теплофизика и аэромеханика. 1998. Т. 5, № 3. С. 319-340.
- OKADA A., LANE D. Enhanced line integral convolution with flow feature detection//Techn. Rep. NAS-96-007. NAS, June 1996.
- FORSSELL L. K. Visualizing flow over curvilinear grid surfaces using line integral convolution//Proc. of the IEEE Visualization'94. IEEE Computer Society, 17-21 Oct, 1994. Washington: D.C., 1994. P. 240-247.
- FORSSELL L. K., COHEN S. D. Using line integral convolution for flow visualization: Curvilinear grids, variable-speed animation, and unsteady flows//IEEE Transactions on Visualization and Computer Graphics. 1995. V. 1, N 2. P. 133-141.
- Strampp W. Mathematische Methoden der Signalverarbeitung/Strampp W., Vorozhtsov E. V. München, Wien: Oldenbourg Verlag, 2004.
- LAIDLAW D. H., KIRBY R. M., DAVIDSON J. S., ET AL. Quantitative comparative evaluation of 2D vector field visualization methods//Proc. of the IEEE Visualization 2001. IEEE Computer Society, Oct. 24-26, 2001. San-Diego: Electronic Edition, 2001.
- ГОНСАЛЕС Р. Цифровая обработка изображений//Р. Гонсалес, Р. Вудс. М.: Техносфера, 2005.


