Обработка экспериментальных данных с помощью делительных сеток
Автор: Авдеева С.О., Короткина М.Р.
Статья в выпуске: 2, 1994 года.
Бесплатный доступ
Компоненты малых и конечных деформаций и поворотов для каждой ячейки микрожидкости были сделаны с использованием экспериментальных значений смещения в узлах микрожидкости. Для этих случаев были построены линии лебеля. Характер изменений смещения в «жестких» и «мягких» областях материала можно получить, анализируя эти линии уровня. Материал находился в состоянии сверхпластичности.
Короткий адрес: https://sciup.org/146211733
IDR: 146211733 | УДК: 639,8
Текст научной статьи Обработка экспериментальных данных с помощью делительных сеток
The competent з of snail and finite deformations and rotations for every cell of microgrid were male using experimental values of displacement tn knots of microgrid. For these cases lines of level were constructed. The character of changes of dtsplarment in "hat'd" and "soft” areas of a material can be got analising these lines of level. The material was under the condition of superplasticity.
Используем данные, полученные в результате экспериментов на одноосное растяжение плоских образцов из некоторого титанового сплава, обсчет которых методом конечных элементов в ликегной аппроксимации поля перемещений приведен в работ-е гц , В статье предлагается другой метод расчета перемещений, ю-тир^ый 1юдр’бН;: изложен в работ ах । ?J .
Испытания приводились он материалах, находящихся ь соси янии сверхпластичнести: материал представляет собой "твердые" серна характерною! размера а ■ ют i до i О мкм>, находящиеся в "мягкой" среде. В прюдессэ деформации квадратная сетка шагом i *i , нанесенная в виде меток <" pw. I-», искажалась и была сфотографирована в три различные момента времени: начальный, промежуточный и конечный.
Возникает задача восстановить поле перемещений внутри ячейки в линейнк-м, в квадратичном и белее высоких порядков 1^.1иб.чижениях не эксиеримент-альным значениям перемещений в узловых точках. Если окажется. пр>и вычисюнии, что коэ^ициенть! квадратичного и би.лее высоких пер'ядк"В нр^иблшений равны ну.лю, тюда внутри ячейки ноле перемещений имеет линейную ашфоксимацию, г. в
Ми г •-н лт Mt'q^iHp. гиг-.^-м ц n;".ni NT- <"•
',6ра6пi f я Экспериментальных данных этом случае реализуются только аффиные преобразования.
В линейном приближении в узловых точках сп+ .по и
_ п* гл пт* , пт* „ пт*
U -Ф к +Ф х , Ц -Ф х 4-Ф х
А тъ пт А А пт пт А т _ п* т ..пт* , пт* _ пт*
и -Ф X +Ф X , и -Ф х +Ф X .
Компоненты перемещения и
координаты узловых точек обозначены
и
и"
и
иГ* ™ -и’
его
и
, ,пгп+ . пт
и -и
cn,m=I,2)
Из <1> и <2> с учетом равенства, выполняемого
на
сетке
1.олучим выражения:
Ф
ф
пгп /{ ф :ТР+ГР
ф
и
1!и -лдюделению комти неты точечного тензора
малых и конечных
деформаций и формулам
тензора вращения
в
узле
<в, пр
расчитываем
W
На рис. для случая T'eilM 'рм-щии
е 4-
.<_ -р
малых
ф
+
К
W
ф +
♦ . <
ф _>, к; »
(. 4 >
< ф
ф
Ф
I:; -ивеjif-я численный
расчет
верхний рис..- и конечных
всех компоненч’ с НИЖНИЙ рис. 1
и пово[-оТ'1В. Контуры на рисунках есть одинаковые
Пт '.-м >! м ■',■ nuj- И' геи и ирей, п дСО'>, J 994 5
5р'Л-.ни компонент деформации и поворотов. Из качественною •анализа рисунков можно принять следующую гипотезу: области замкнутых линий уровня, по всей видимости, связаны с деформацией 'твердых" частиц, а разомкнутые ..... с деформацией "мягкой" среде, .жадернмонтально эту гипотезу подтверждает тот факт, что в ююг^ втиснутых линий уровня находится риска делительной сетки, t изображенная в виде У-f что хорошо видно на всех рисунках.
При численной ибрат/гке экспериментальных данных ио формулам его согласно рис. г, л, 4,г, 6 можно сделать предварительное заключение: 1% компоненты малых и конечных деформаций и поворотов описывают картину деформирования качественно одинаковым образом, 2% компоненты конечных деформаций и поворотов описывают поведение "мягкой” фазы, а "твердая" фаза качественно адекватно описывается компонентами и малых и конечных деформаций и поворотов.
Таким образом, используя экспериментальные данные, полученные с помощью делительных сеток, вычисляем компоненты неФ^рма:1им и поворотов и строим линии уровня. Рформулирчем обратную задачу. Восстанавливаем реальную структуру исследуемого материала в .процессе деформирования: положение и деформащи "гг^р),цых” частиц - замкнутые линии уровня, деформации "мягкой"
Фазн: - незамкнутые линии
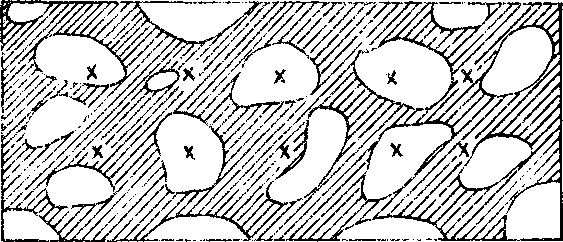
Рис.I,
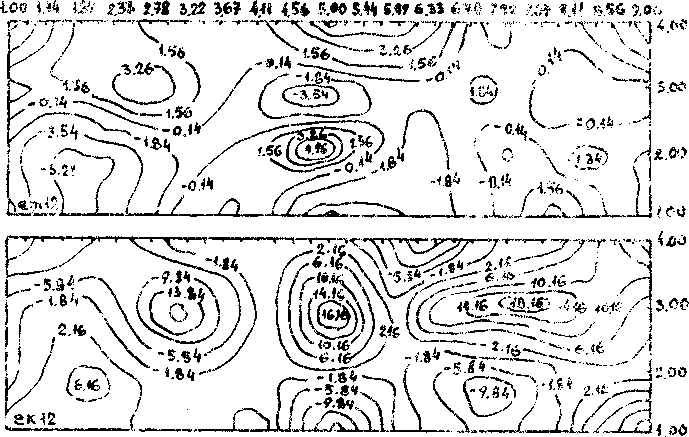
РИС.2.
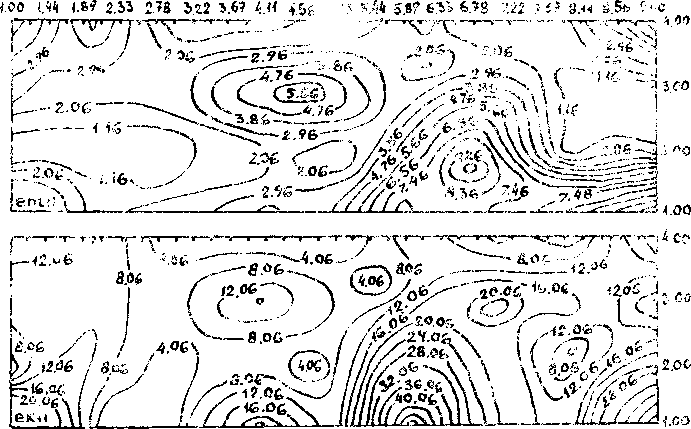
Рис.З.
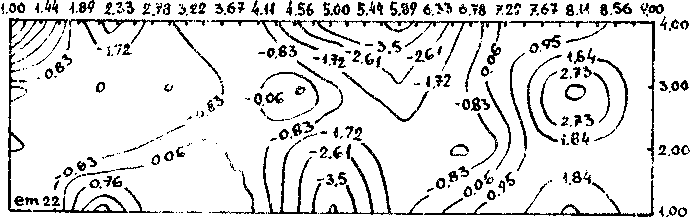
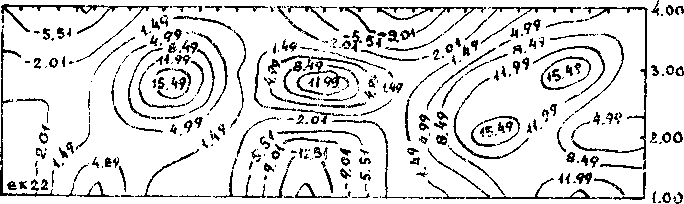
Рис. 4.
ЮС Ю4 <8? 2.33 $36 3.22 3.6#4Н 4.56 5.66 554 W6.33 638 7.22 Z6P8.H 8.56 »оо
■1^ '-у1 «П|Ч11 -у^.- у.*,» .-1r***Vм^чл¥~м■a^a,mм«*^^■^-~^v~eu,ж^r*^^',^ir~v’¥-~, v'w— "8 —"ч»"**г '»«~w— »^^ Ti^-*a-*w—-ге^^»*^>и Л
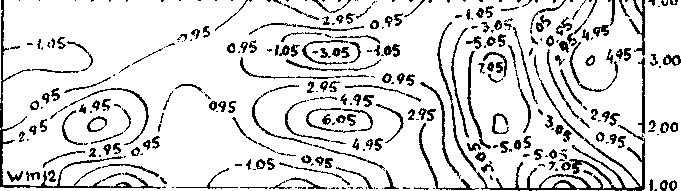
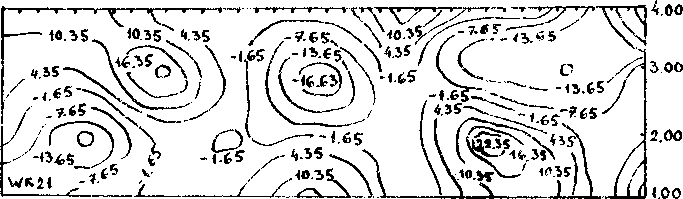
Рис.5.
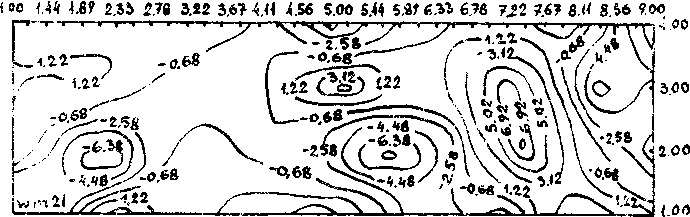
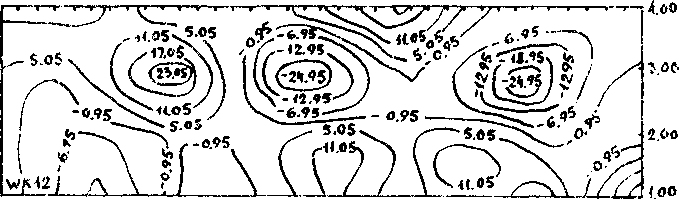
РИС. в.


