Обработка сигналов на основе модели в виде обобщенного нелинейного уравнения Шредингера

Нелинейные фазовые фильтры (НФФ) [1-2] представляют собой сравнительно новый класс устройств цифровой обработки сигналов. Они являются достаточно универсальными и могут использоваться для решения ряда радиотехнических задач, в частности для компенсации дисперсионных искажений в различных каналах связи, в том числе и волоконно-оптических [3-4]. НФФ обычно строятся на основе модели в виде нелинейного уравнения Шредингера (НУШ) следующего вида:

ат а2т

ар аг

где характеризующая вид нелинейности фильтра, – постоянный параметр. Уравнение (1) используется в различных областях физики для описания нелинейных волновых процессов. В частности, в нелинейной оптике оно описывает процесс распространения оптических импульсов с комплексной огибающей       по нелинейным оптичес ким волокнам (ОВ). В этом случае нелинейная функция выбирается квадратичной (такая нелинейность ОВ называется кубической)

здесь – параметр нелинейности ОВ. Уравнение (1) в этом случае принимает вид [5]:

ап ат2 1 1

здесь имеют смысл, соответственно, пространственной и временной координат, а – параметр, влияющий на степень дисперсионного уширения оптического импульса в процессе эволюции.

Нелинейный фазовый фильтр представляет собой устройство цифровой обработки сигналов, которое можно рассматривать как цифровой аналог (1) или, в частности, (2). Он реализуется на основе метода расщепления по физическим факторам [5] и, в простейшем случае, реализуется в виде двух последовательно соединенных звеньев – нелинейного и линейного. Эти звенья имеют соответственно коэффициент преобразования мгновенных значений и импульсную характеристику

g(T) = g0 exp

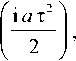
или соответствующую передаточную функцию

G(ico) = exp (ЧаДрю2)

где ои g0 – постоянные коэффициенты вида

1 а ⁼------,

2аЛг]

g0 = , л ~ехр ^яаДг]

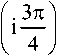
Ат] – шаг по пространственной координате .

Реализация НФФ на основе моделив виде обобщенного НУШ

Модель нелинейного оптического волокна вида (2) является достаточно приближенной. В ней не учитываются как дисперсионные, так и нелинейные эффекты высших порядков. Более точно нелинейное ОВ описывается обобщенным НУШ

Этот коэффициент играет важную роль, так как определяет знак дисперсии ОВ и называется дисперсией групповых скоростей (ДГС). Если Рэ > О , дисперсия является нормальной, а если р, < О – аномальной.

Рассмотрим способ построения НФФ на основе уравнения (9) с целью повышения эффективности временной компрессии импульсных сигналов. Эта модель также не учитывает нелинейные эффекты высших порядков, такие как дисперсия нелинейности и запаздывание нелинейного отклика [3]. Но из-за трудности их учета при реализации НФФ, ограничимся только указанной моделью. Запишем выражение (10) в развернутом виде:

а2 а3 а4

Д(Т) = -а2—+ icc3—+ а4—...-/(Ч/). (15)

i—= ^(T)T, ap v 5

Выражение (9) при этом примет вид

где 2У(Т) – нелинейный дифференциальный оператор вида:

. ат а2т . а3т а4т

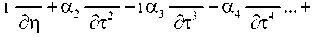
/(Т)Т = 0 (16)

^№=f (-оч^г-ут,   (10)

дш R         /5'Ч> i —-^Н)'а„—+ /(Т)Т = 0.   (17)

ап “      ат

в котором аг – дисперсионные параметры порядка /', определяемые выражением:

Очевидно, что характеристика преобразования мгновенных значений нелинейного звена при этом не изменится:

1 Г 2 W arp) ' 2P0r!^P2J 1^®'Z где

Н(т)= exp[i/(T)].       (18)

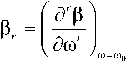
Для вычисления характеристик линейного звена удобно рассмотреть линеаризованное уравнение Шредингера, полученное из (15) при условии /(Т) = 0:

– коэффициенты разложения постоянной распространения ОВ Р(со) в ряд Тейлора вблизи центральной частоты соо спектра импульса на входе ОВ с комплексной огибающей :

.ат

1-------- дг|

а2т . а3т а4т

—- + 1а,—^ + а, —- +

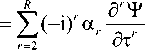
Найдем преобразование Фурье левой и правой

Р( со) = и(со) — = ро + Р, (со - со,,) + ^- р2 (со - соо)2 +... (13)

Коэффициент Рз определяется показателем преломления кварца «(со) и зависит от длины волны X и скорости света в вакууме с и определяется выражением

частей (19):

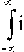
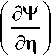
e”™xdT =

. d i— dx\

| Т(г|,т)е ™"dt

. c/T(r|,ico) dv\

сТ       1 Г. dn    d~n

—v   =- 2— + со—7

5® ут=ю с< ^® с7аг со d"n X3 d2n с de? Inc2 dX2

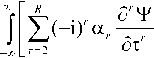
R          ” Д' cp e"mTdT = Е<-*)' “r J7a-e"“WT =

= ^(-i)^rcx_r -(ico)' T(i],ico) = T^a_rco^r, r=2                                     r=2

здесь – преобразование Фурье огибающей . Приравнивая правые части (20) и (21) получим обыкновенное дифференциальное уравнение

.уф ~ R или с/Ф • которое легко интегрируется:

Ф = C exp

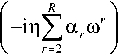
Постоянную интегрирования C определяем из начального условия:

Подставляя (25) в (24) получим

следовательно

G(io) = exp|-iAp(a2co2 + a.3co3 + ... + arco' )} =

= exp(-iAp аэ co2 ^ • exp(-iAp a3 co’) ■...

•exp(-iAp a_R ro^R ) = G₂(ico)- G₃(ico)-...-G_ff(ico) = ^^

, r=2

где G,.(io)) = exp(-iApar co' ).

Таким образом, простейший НФФ, основанный на модели вида (9) – (10), можно реализовать в виде одного нелинейного звена с характеристикой преобразования мгновенных значений вида (4), а также r последовательно соединенных линейных звеньев с передаточными функциями вида (32). Ввиду сложности такого линейного звена, а также с целью уменьшения задержки сигнала в нем (которая будет расти с увеличением R ) целесообразнее реализовать линейное звено в виде одного фазового звена с полиномиальной фазочастотной характеристикой (ФЧХ):

R cp(co) = arg[G(io)] = -iAp^arco' = r = 2

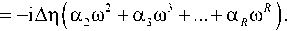
R

Ф = Фо exp -ip^op

CL to

Таким образом, искомая передаточная функция линейного звена НФФ с произвольным пространственным параметром определится выражением

G(p, i co) =

Ф(р,1со) ^оСфМ

f     R

= exp -ip^cpco'

V    r=2

Передаточная функция линейного звена, входящего в НФФ, должна иметь достаточно малый пространственный параметр

[2]. Для такого звена функция (28) примет вид

G(ico) = G(Ap,ico) = exp -iAp^arcor

В частном случае, когда выражение (29) будет иметь вид

Это выражение совпадает с (6) при условии .

В общем случае при (29) можно записать в развернутой форме

Выводы

Линейное звено НФФ легко может быть реализовано в цифровой форме с использованием алгоритма быстрого преобразования Фурье [1], аналогично простейшему линейному звену с передаточной функцией (30), имеющему квадратичную ФЧХ. Для дальнейшего увеличения эффективности временной компрессии сигналов число таких наборов нелинейных и линейных звеньев необходимо увеличить. Кроме того, возникает необходимость совместной оптимизации параметров линейного и нелинейного звеньев с целью повышения эффективности его работы. Но эта задача выходит за рамки данной статьи и требует дополнительного исследования.