Обработка сигналов термического зеркала при стационарном возбуждении

Методы фототермической [1] и оптоакустической [2] спектроскопии перспективны в ряде нестандартных приложений, включающих исследование веществ с крайне слабым [1, 3, 4] или, наоборот, очень сильным поглощением [5, 6], определение физических параметров (например, коэффициентов теплопроводности и термического расширения) [7, 8], исследование оптических нелинейных эффектов (например, светопоглощения и люминесценции) [1, 9, 10], в том числе в присутствии наночастиц металлов [11]. Данные приложения дополняются классическим применением фототермической спектроскопии для анализа следовых количеств веществ [12]. Для обработки экспериментальных результатов, полученных методом спектроскопии термического зеркала, разработан громоздкий математический аппарат с решением обратной задачи, который значительно затрудняет более широкое применение методики. Стандартный метод определения параметров модели (некоторые из которых являются актуальными характеристиками образца) заключается в расчете сигнала при их вариации с оптимизацией описания эксперимента. Цель настоящей работы заключается в создании и апробации менее трудоемкого способа решения обратной задачи спектроскопии термического зеркала при стационарном возбуждении.

Теоретические основы спектроскопии термического зеркала в случае Гауссового распределения интенсивности в возбуждающем и зондирующем лазерных пучках непрерывного действия были разработаны в [13]. Проанализированы предельные случаи сильного поглощения, слабого поглощения возбуж-

дающего излучения, а также наиболее общий случай Бугеровского профиля поглощения света с показателем A [13]. В рамках модели процесса локальный нагрев вещества непрерывным излучением, которое включается в начальный момент времени ( t = 0), вызывает неоднородное распределение температуры и локальную деформацию поверхности образца, играющую роль искривленного зеркала. Относительно небольшое увеличение температуры в несколько градусов приводит к деформации на уровне нанометров и дифракции отраженного пучка, отслеживаемой по изменению интенсивности в его центре в плоскости детектора. Спектроскопия термического зеркала отличается слабым воздействием на образец, поэтому на ее основе можно создать методы неразрушающего контроля исполнительных устройств на основе энергетических материалов, например, капсюля оптического детонатора [14– 16]. Данные подходы могут быть особенно эффективны для исследований непрозрачных образцов при совмещении с методами спектроскопии отражения [14, 17– 19].

В [13] с использованием метода интегральных преобразований в цилиндрической системе координат получены выражения для вычисления поля температуры ( T ), нормальной компоненты деформации поверхности ( u z ) и сдвига фазы в пучке зондирующего излучения (Φ). Уравнения для деформации и сдвига фаз имеют вид [13]:

го uz (r, t) = -2aT (1+v) ja2 f1 (a, t) J0 (ra)da,(1)

Ф( r, t) = (4n/X p) Uz (r, t),(2)

x    27 T(a,X,t) л f1 (a, t ) = Ъj ^27x^dX, где αT – коэффициент термического расширения вещества, ν – коэффициент Пуассона, r – радиальная координата, отсчитываемая от центра пучка, λp – длина волны зондирующего лазерного излучения, T(a, X, t) - Ханкель - Фурье-образ температурного поля в момент времени t, где преобразование Фурье выполняется по глубине образца z, а Ханкеля – по радиальной координате r. В случае Гауссового распределения интенсивности W (в Вт/см2) в возбуждающем пучке c радиусом w и суммарной мощностью P0: W = (2P0/ пw2)exp(-2r2/ w2) - функция f 1(a, t) имеет вид:

t 2

f (^a , t ) = J Q — • 0 4

exp (-a2 w 2/8) a2 - A2 X erfcx(x), заменяющей exp(x2)^erfc(x) [13]. Такая замена делает вычисления более удобными, устраняя необходимость вычислять множитель exp(- (A2w2/4)-(t/tc)), стремящийся к бесконечности в ряде практических случаев.

Сигнал термического зеркала, в качестве которого используется относительная интенсивность в центре зондирующего пучка в плоскости детектора, в соответствии с теорией дифракции имеет вид [20]:

_S = I ( t )

I ( t = 0 )

M

J exp [-(1 + iV) g - i Ф( g, t)] dg

M

J exp H^{1 + iV} ) g ] ^d g

{ /    2 2 A

I aw т I , exp----• erfcx

I 4 tc)

( л

Aw т

2 \t

V c < 7

= (1 + V2 )• J exp [-(1 + iV) g

M

- i Ф( g, t)] dg

-(A/a) erfc ((aw/2)т/tc)} dT, где Q0 = 2P0AфT(пw2c)-1, tc = w2(4D)-1 - характерное время тепловой разгрузки зоны возбуждения, фT - доля энергии падающего излучения, которая диссипирует в тепло (тепловой выход), c – объемная теплоемкость, D – коэффициент температуропроводности. Распределение сдвига фазы в момент времени t определяется выражением:

Ф(g, t) = -9A J a2 exp (-a2 w2/8 )x

0                                            (5)

x f (a, t )• Jo (wa ^g) da,

где m = ( w p / w )² – квадрат отношения радиусов зондирующего и возбуждающего пучков, g = ( r / w p )² – квадрат радиальной координаты, нормированной на радиус зондирующего пучка лазера. J 0 – функция Бесселя, 9 = ( P 0 a T ( 1+ v ) ф _T )/ Dc X _p , и функция f ( a , t ) имеет вид:

f ( a , t ) = (2 ^t/ t _c Aw exp ( -a ² w²t /4 t _c ) ) ^

^Jna ² ( a ² - A ² ) - (( t / t _c ) Aw ² • erfc ( ( a w /2) Jt /t c ) ) ^

^a ( a ² - A ² ) + (2/ a ³ ( a ² - A ² ) 2 ) { A ( A ² - 3 a ² ) x     (6)

x erf ( ( a w /2) Jt / t _c ) + 2 a ³[1 - exp ( -a ² w²1 /4 t _c ) x

x

В отличие от [13] мы предлагаем переопределить параметр θ так, чтобы он получался безразмерным, и выделить из него величину показателя поглощения. В результате параметр θ связан только с теплофизическими свойствами образца и мощностью возбуждающего излучения. Функция f (a, t) в выражениях (5) и (6) отличается от f1(a, t), введенной в (4), вынесенным постоянным множителем (Q0 / 4)·exp(-α2w2/8). Формулы (4) и (6) записаны с использованием функции где V – отношение положения образца относительно фокуса зондирующего пучка к его конфокальному расстоянию.

Таким образом, расчет сигнала термического зеркала в каждый момент времени включает вычисление интеграла (6) с последующей подстановкой результата в интеграл (7). Пример результатов расчета при значениях параметров θ = 3637,1 P 0 , t c = 2,47 мс, w = 71 µм, A = 3 см^-1, m =25, V = 6,71 и мощности излучения P 0 = 25 мВт приведен на рис. 1 (кривая 1).

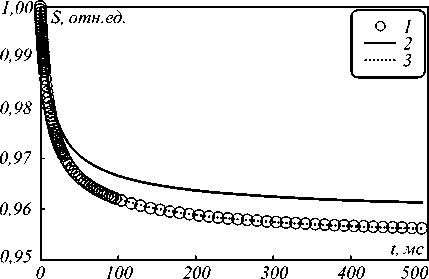
Рис. 1. Рассчитанные сигналы термического зеркала: результат моделирования (1), расчёт при определении параметров по одно- (2) и двухстадийной (3) методикам

Хорошо видно, что результирующая кривая представляет собой монотонную зависимость с отрицательной производной, которая стремится к стационарному значению при t →∞. Данное поведение связано с установлением стационарного температурного поля и соответствующего стационарного распределения деформации поверхности. При обработке экспериментальных данных необходимо выделить набор значений сигнала в различные моменты времени и выполнить их описание расчетной зависимостью, например, при минимизации суммы квадратов отклонений. В силу необходимости последовательного расчета двух интегралов решение обратной задачи в спектроскопии термического зеркала требует значительных вычислительных затрат.

2. Характерные особенности сигнала термического зеркала

Рассмотрение зависимости (рис. 1) приводит к выводу, что ее можно охарактеризовать двумя значениями: начальный наклон и стационарное значение сигнала. Получим соответствующие выражения, которые далее можно будет использовать для обработки экспериментальных результатов.

В первом случае сигнал и соответствующий сдвиг фаз малы, что позволяет выполнить разложение экспоненциального члена с сохранением только линейного слагаемого: exp[- i Ф(д, t)] = 1- i Ф(д, t). Получим производную сигнала по времени в пределе t →0.

F1 (Aw) = J exp

-

1 У I x

+ ^ •

2 J 4

sin [ ^ Vx / 4 ] d x Aw + V x

В выражении (13) интегрирование осуществляется по безразмерной переменной x = ( a w )². При Aw << 1 данная функция стремится к пределу:

I  Г                 9                9 ""I-1/2

1 im_o F 1 ( Aw ) = V2 n-1 ( 1/2 + ^ ) + ( ^ V ) l x

x

J ( 1/2 +^ ) 2 + ( ^ V ) 2 - ( 1/2 + ^ )

1/2

d ^B = (1 + V d t            d t

----V + i 9 A f Y ( a , t ) x

1 + V ^{2       J} ₀ ^{v 7}

x J exp ( - ( 1 + iV ) g ) J о ( w a Jmg ) d g d a ,

где Y( a , t ) = a ²exp(- a ² w 2 /8) - f ( a , t ) введено для сокращения записи. Вычисление интеграла по g приводит к выражению:

На рис. 2 представлены рассчитанные зависимости F 1 ( Aw ) при значении m = 20 и V , равном 5, 10 и 15 (кривые 1, 2 и 3 соответственно), кружками обозначены значения, полученные при расчете по предельному выражению (14). Из рис. 2 следует, что отклонение от предельного значения при Aw < 0,1 составляет менее 10%.

Перейдем к оценке стационарного значения сигнала термического зеркала. В области больших t предел функции Y ( a , t ) составляет:

J exp (-(1 + iV) g) J о (waJmg) dg =

lim Y (a, t ) = 2 - t ^7 X 7

2 a + A a ( a + A ) 2

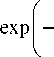
2 2 A a w I

.

8 J

= exp[(-w2 a 2^/4)/(1 + V 2)]x x |cos (w2 a2q V/4) + V sin (w2 a2q V/4) + + i (sin (w2 a2^ V/4) - V cos (w2a2^ V/4))

где £ = m /(1+ V 2 ). Подставляя (9) в (8) и раскрывая квадрат модуля, имеем:

dB = -29A?

df J t0

d Y ( a , t ) d t

w 2a2^ - e ”

. 1 w2a2qV I , sin ----— da + k 4 J

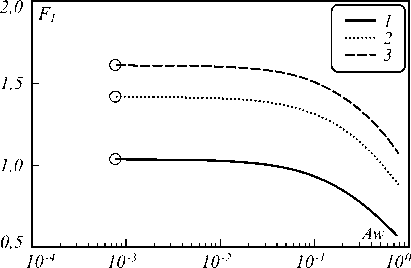
Рис. 2. Рассчитанные зависимости F1(Aw) по выражению (13) при значениях V= 5 (1), 10 (2) и 15 (3)

d

+— d t

7            w 2a22

9 A J Y ( a , t ) e ” B 1

I w ²a²^ V | . ---— da +

I ^{4 J}

Фазовый сдвиг в этом случае определяется выра-

жением:

d

+— d t

7             w ²a²E     f .2²П7 A

9 A f Y ( a , t ) e ⁴ B₂ w ^a ^ V d a

0                    k          J где B1(x) = sin(x)–Vcos(x), B2(x) = cos(x)–V sin(x). Функция Y(a, t) стремится к нулю в пределе t^0, но имеет конечную производную:

dY(a,t)   1 aw2      ( a2w2I lim---------=----exp I--I.           (11)

t ^⁰ d t      t a + A     (    8 J

Поэтому в (10) второе и третье слагаемые стремятся к нулю при t →0 в отличие от первого. Объединяя выражения (11) и (10), имеем формулу для начального наклона временной зависимости сигнала термического зеркала:

d В /d t\_t . = - ( 9 / t c ) Aw - F 1 ( Aw ) ,                    (12)

где введена функция F 1 ( Aw ):

Ф = - 2 9- 1 ₂ ,

где

7 Aw 2 x + Aw     ( x ²)   / I---\

I 2 = I--;------- ТГ • ^exp I ^-— I • J о ( xjmg ) d x .⁽¹⁷⁾

• о ^x ( x + Aw )       k ⁸ J

• 3. Обработка сигнала термического зеркала

Согласно выражениям (12)–(17) для вычисления начального наклона требуется вычислить только один интеграл (13), а стационарного значения сигнала – два интеграла (17) и (7) последовательно. Поэтому для их определения требуется значительно меньший объем вычислений, чем для величины сигнала в произвольный момент времени, причем сокращение связано в основном с использованием начального наклона.

При экспериментальном измерении сигналов термического зеркала значения величин m, V, P0, w и Xp определяются используемой аппаратурой. Параметры c, D, А, фT, aT и v определяются используемым образцом, и некоторые из них можно получить при сравнении экспериментального и рассчитанного сигналов термического зеркала. Применение спектроскопии термического зеркала для оценки параметров люми-несцирующих стекол было описано в работе [8]. На практике используется аппроксимация экспериментального сигнала расчетной зависимостью при вариации параметров 6 и tc. На основе величины 6 может быть оценен один из параметров: теплоемкость, коэффициент термического расширения и тепловой выход, - если остальные известны. Характерное время тепловой релаксации непосредственно применяется для определения коэффициента температуропроводности. В случае люминесцирующих стекол целевыми параметрами являются тепловой выход и коэффициент температуропроводности. При этом показатель поглощения обычно измеряется заранее стандартными методами.

Рассмотрим случай, когда показатель поглощения известен и определяемыми параметрами являются 6 и t c . Тогда выражение (16) может быть использовано для оценки величины 6, а уравнение (12), содержащее отношение 6 / t c , - для определения t c . При известном А интеграл (13) необходимо вычислить только один раз, поскольку он не зависит от варьируемых параметров, что также уменьшает объем вычислений.

Первичный вариант обработки заключался в следующем. Для сигнала определялся начальный наклон с использованием участка от 0,5 до 20% амплитуды. В качестве стационарного значения выбиралась минимальная величина сигнала. Затем вычислялись интегралы (13) и (17) и определялось отношение 6 / t c по формуле (12). Наконец, численно решалось нелинейное уравнение (7) с подстановкой (16) для определения 6. Результаты применения методики к модельному сигналу представлены на рис. 1 в виде зависимости, рассчитанной при оцененных параметрах. Из рис. 1 следует, что аппроксимированная зависимость начинает отклоняться от рассчитанной по полной модели только в области больших значений времени. Анализ результатов позволил выявить, что оценка характерного времени тепловой релаксации t c получается достаточно точно. В то же время типичная ошибка при оценке параметра 6 составляет ~7%. В качестве причины отклонения можно указать взятие минимального значения сигнала как стационарного. Стремление сигнала к стационарному значению оказывается недостаточно быстрым, что и приводит к заниженной величине 6. При выполнении измерений обычно длительность отдельного опыта ограничена. Кроме того, при больших значениях времени может стать значимой тепловая разгрузка мишени в окружающую атмосферу, которая не учитывается моделью (1) - (6).

Для устранения данных недостатков была предложена двухстадийная процедура. На первой стадии, в соответствии с исходным вариантом обработки, оп- ределялась величина tc и делалась первичная оценка параметра 6. Затем, для уточнения параметра 6, численно решалось нелинейное уравнения для последней точки на кинетической зависимости сигнала по модели (1)-(7) при использовании определенного на первой стадии значения tc. Рассчитанная кинетическая зависимость сигнала при определенных с помощью двухстадийной процедуры параметрах приведена на рис. 1. Хорошо видно совпадение зависимостей 1 и 3, свидетельствующее о правильности работы методики в идеализированном случае.

Предложенная двухстадийная методика использовалась для обработки экспериментальных сигналов термического зеркала, предоставленных доктором наук Витором Зануто (г. Маринга, Бразилия) и профессором Стефеном Биалковски (г. Логан, США). В качестве образца использовалось люминесцентное стекло толщиной 2,6 мм, допированное америцием. Возбуждение образца осуществлялось пучком аргонового лазера (длина волны - 488,0 нм), зондирование - пучком гелий-неонового лазера (длина волны -632,8 нм). Схема установки представлена в [21]. Показатель поглощения стекол на длине волны 488,0 нм составлял 5 см^-1, на длине волны зондирующего лазера поглощение было пренебрежимо мало. Измерения выполнены при значениях радиуса пучка аргонового лазера на поверхности образца w =46 рм, V =3,7, m = 27,5 при варьировании мощности возбуждающего излучения. Обработка проводилась по стандартной методике [13] (расчет величины сигнала при нескольких значениях времени и минимизация суммы квадратов отклонений) и предложенной в настоящей работе двух-стадийной методике.

Примеры обработки экспериментального сигнала термического зеркала (кривая 1) при мощности возбуждающего излучения 50 мВт с помощью предложенной двухстадийной (кривая 2) и стандартной методик (кривая 3) представлены на рис. 3.

Рассчитанные зависимости практически не отличаются, что свидетельствует о близости получаемых параметров. В таблице приведено сравнение параметров, полученных для сигналов термического зеркала с различной мощностью возбуждающего пучка.

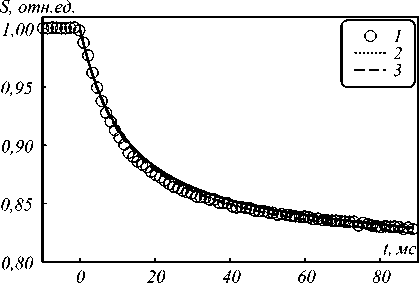
Рис. 3. Результаты обработки экспериментального сигнала термического зеркала (1) по предложенной (2) и стандартной (3) методикам

Табл. Сравнение результатов обработки экспериментальных сигналов термического зеркала по предложенной и стандартной методикам

P 0 , мВт	Стандартная методика		Предложенная методика
	θ / P 0	tc , мс	θ / P 0	Отклонение, %	tc , мс	Отклонение, %
50	20,89	1,326	21,46	2,7	1,310	1,2
60	20,92	1,323	21,64	3,3	1,257	5,0
70	21,33	1,364	21,85	2,4	1,307	4,1
80	21,60	1,340	21,92	1,4	1,270	5,2
90	22,02	1,378	22,58	2,5	1,283	6,9
100	22,11	1,333	22,29	0,8	1,303	2,2
Среднее	21,48	1,344	21,96	2,2	1,288	4,1

Типичное отклонение параметров, полученных при различных способах обработки данных, составляет несколько процентов. Наибольшее отклонение для параметра t c равно 6,9 %, а для параметра θ –3,3 %. Величина характерного времени тепловой релаксации по предложенной методике получается немного меньше, а амплитудного параметра – больше, чем по стандартной. Типичная погрешность определения параметров в методе термического зеркала составляет 10 % [7, 8] и превышает полученное отклонение. Метод использования характерных особенностей сигнала может быть также применен для получения нулевого приближения с дальнейшим расчетом по стандартной методике для значительного уменьшения количества шагов при оптимизации описания с варьированием параметров.

Заключение

Рассмотрены основные особенности сигналов термического зеркала при стационарном лазерном возбуждении. Получены и апробированы выражения для начального наклона и стационарного значения сигнала. Предложена процедура обработки экспериментальных сигналов термического зеркала, основанная на использовании начального наклона сигнала и его стационарного значения. Методика верифицирована на модельных сигналах. Выполнено сравнение результатов определения параметров экспериментальных сигналов с помощью предложенной и стандартной методик. Сделан вывод, что использование начального наклона и стационарного значения сигнала позволяет значительно сократить вычислительные затраты при определении параметров модели термического зеркала без потери точности.

Авторы благодарны доктору Витору Зануто и профессору Стефену Биалковски за предоставленные экспериментальные сигналы термического зеркала, помощь в обсуждении результатов. Работа выполнена при финансовой поддержке Министерства образования и науки РФ (НИР № 3.5363.2017/8.9).