Обработка сигналов в радионавигации как обратная некорректная задача с применением методов регуляризации

При разработке радиотехнических систем чаще всего встает вопрос о том, каким образом максимально уменьшить помехи (это могут быть электромагнитные наводки, внутренние помехи оборудования, погодные условия и т. д.), либо выделить полезный сигнал на фоне шума.

Это можно сделать технически, путем совершенствования аппаратуры: увеличение размеров антенны, создание прецизионных и чувствительных датчиков детектирования сигналов, увеличение мощности передатчика и т. д. Однако на практике такой подход не оправдывает себя (разработка совершенной аппаратуры финансово не выгодна, а увеличение мощности передатчика может затронуть соседние каналы передачи сигнала или вообще «заглушить» приемник).

Поэтому чаще всего прибегают к математической обработке сигналов, и, в частности, к задаче редукции. Задача редукции, как правило, требует определения аппаратной функции канала измерения. Но даже при известной аппаратной функции во многих случаях невозможно определить точные параметры исходного сигнала, так как решение является неустойчивым и требует регуляризации. Обычно математическая обработка выполняется на универсальных компьютерах, чаще всех на персональных, но со стремительным развитием специальных вычислительных устройств позволило применять математическую обработку в фотоаппаратах и других миниатюрных устройствах.

В радиотехнике при определении параметров сигналов чаще отдают предпочтение методам, основанным на постобработке массива информации о поведении сигнала, например, методы адаптации, компенсации локальных сигналов-помех, методы, использующие собственные значения и векторы симметрично ковариационной матрицы, теоретико-информационные методы и т. д. Эти методы решают некоторые задачи повышения помехоустойчивости и помогают добиться значительных результатов [1], имея при этом существенный недостаток: они не могут дать оценку потенциальной возможности разработанной аппаратуры в пределах точности параметров сигнала, то есть используют принцип «что сделали, то и получили», а применяемые методы постобработки улучшают только вероятностные характеристики обрабатываемых сигналов.

Методы решения задачи редукции, основанные на определении устойчивого решения обратных некорректных задач, приближают к определению истинных параметров сигнала и определяют потенциальные возможности разработанной аппаратуры.

• 1.    Постановка задачи редукции

Измерительное устройство, будь то радиолокатор, телескоп, радиотелескоп, томограф, фотоаппарат, и т. д. характеризуется тем, что измеренный сигнал отличается от истинного: близкие максимумы слабо разрешены, слабые максимумы вследствие наложения шума невозможно определить. Это обусловлено тем, что аппаратная функция, которая, например, в радиотехнике в большей степени является диаграммой направленности, не имеет бесконечно узкую форму, а имеет некоторую ширину и тем, что на всю систему в целом действуют помехи различной природы.

Для математической обработки при условии f – результат измерений, а y – искомая, неизвестная функция, характерно следующее соотношение:

f = АУ, где А – математический оператор (например, обратная матрица, а в случае обработки сигналов – система линейных или линейно-нелинейных алгебраических уравнений).

Тогда обратная задача будет иметь вид

• У = а - 1 f .                                                                                         (1)

На практике обратная задача может принять вид интегрального, дифференциального уравнения, системы линейных алгебраических уравнений, системы линейно-нелинейных алгебраических уравнений, и так далее. Но чаще всего такие задачи описывают интегральным уравнением Фредгольма I рода:

b

• j A ( x, s ) y ( s ) ds = f ( x ), c <  x <  d,                                                                 (2)

• 2.    Анализ существующих методов обработки сигналовс использованием обратных некорректных задач

a где A(x, s) – ядро; f (x) – выходной сигнал; y(s) – искомая функция (входной сигнал); x и s – параметры (линейные или угловые координаты, время, температура, частота и т. д.); c и d – область измерения f(x), а a и b – область поиска y(s).

Такое уравнение применяют в спектрометрии, а также для разрешения протяженных сигналов, при моделировании распада клеток и так далее. Также модификации этого уравнения, такие как интегральное уравнение Фредгольма I рода с разностным ядром могут применять для синтеза магнитного поля оси катушки ЯМР томографии. Существует также интеграл Фредгольма II рода, который применяется для восстановления сигнала в системе, не являющейся динамической [1]. Все эти уравнения построены на теории Фредгольма [2].

Обратные задачи позволяют без применения каких-либо изменений в антенне, в спектрометре или в другом измерительном приборе разрешаемость тонких линий в спектрометрии или разрешение близких целей в радионавигации, реконструировать смазанные и несфокусированные изображения. Но обратная задача является, как правило, некорректно поставленной задачей, не имеющей устойчивого решения.

По Адамару задача считается корректно поставленной, если выполняется три условия: математическое решение задачи существует; решение единственно; решение устойчиво.

Для решения обратных некорректных задач используют методы регуляризации, например, метод регуляризации Тихонова [3]. Стоит отметить, что существуют и другие методы регуляризации, такие как фильтр Калмана – Бьюси, параметрическая фильтрация Винера и др., но именно регуляризация Тихонова, благодаря тому, что не требует большого количества априорных сведений об измеренных данных, нашла широкое применение в различных областях знания.

Математическая обработка применяется в различных областях науки: томографии [4], где без математической обработки невозможно определить плотность вещества, в гидролокации подводных лодок [1], где большую антенну с узкой характеристикой направленности построить затруднительно, в радиотехнике [5], где автор разрешает известный парадокс в теории оценки целей и координат по критерию максимального правдоподобия, когда с увеличением числа целей увеличивается и правдоподобность оценки, с помощью методов регуляризации для некорректных задач. Полезный сигнал x(s) в этом случае является наложением комплексных сигналов u(s,p) от источников, распределённых в некотором фазовом пространстве, поэтому x (s)=J A (p) u (s, p),                                                                              (3)

где A ( p ) – неизвестная плотность комплексных амплитуд сигналов от источников (центров рассеяния).

При приеме такого сигнала в белом шуме критерий максимального правдоподобия приводит к уравнению для оценки A ( p )

J C ⁽ p , P 1 ) A ⁽ P 1 ) dp i = £ y ⁽ s i ) u '( S j , p ),                                                               ⁽⁴⁾

i где С(p1,p2) = ^u'(Sj,p)u(si,p2) - функция взаимной корреляции сигналов от источников с i разными параметрами, а y(s1) – функция правдоподобия.

В правой части (4) результат корреляционной обработки совокупности сигналов (умножения на ожидаемые сигналы в каждой точке приема и суммирования). Задачи, описываемые (4), относятся к классу некорректных, так как небольшие изменения правой части могут изменить искомое решение, то есть решение является неустойчивым [5].

В другой работе [6] исследуются методы регуляризации Тихонова и его идейное продолжение l ₁ и l _p -регуляризации в совокупности с переопределением базиса (для сведения нелинейной задачи к линейной) применительно к задаче радиопеленгации. l _p -регуляризация в отличие от метода регуляризации Тихонова требует еще меньшего количества априорных сведений, поэтому его удобнее использовать на практике. Недостатком является высокая требовательность к вычислительным ресурсам из-за большого количества многомерных преобразований

A ( 0 , р ) u ( t ) + n ( t ) = y ( t ) , t = { t i ; t 2 ;...; t_T } ,                                                                      (5)

где n ( t ) - аддитивная помеха с гауссовым распределением; A ( 0 , в ) - матрица, характеризующая набеги фаз на элементах антенной системы с учетом ее конкретной геометрии и вида сигналов [6].

Некорректность (5) заключается в том, что отношение максимального и минимального отношения собственных чисел матрицы составляет порядка 107 [6]. Поэтому здесь нельзя применять классические методы решения задачи радиопеленгации, например, такие как критерий наименьших квадратов.

В качестве аппаратной функции в [6] предлагается использовать для круговой антенной системы при общем виде решаемой задачи (5) следующую аппаратную функцию

A (0,Р) = [ a (01, Pi) a (02,Pi) ... a (0 к, в к)], где

• . Г f 2 n R )    ,        ,        1

• ^- j l Ф о +1 -у— I cos ( ⁰ к ^- Y m ) cos ^в к I

• 3.    Варианты некорректных задач в радионавигации

am (0 к ,в к ) = Fm (0 к ,в к) e V Vx)              ], где Fm (0к, вк) - диаграмма направленности одного элемента антенной системы; ф0 - начальная фаза сигнала; X - длина волны сигнала; 0к, вк - азимутальные углы и углы места соответственно; Y - угол между линией отсчета пеленга и линией, проведенной через центр окружности i элемента круговой антенной системы.

В работах [5, 6] решение обратных задач можно применять для повышения разрешения измерения радионавигационных параметров наряду с классическими методами, а также для повышения помехоустойчивости.

Существует как минимум три подхода постановки некорректной задачи в радионавигации.

Первый подход предполагает априорные сведения об аппаратной функции, при этом задача радионавигации рассматривается как

• -1к

• V    А 1 V ™;

”0 = А 21 0 _Изм ;                                                                                    (6)

• R    = А 3 - 1 R изм ,

где VU3M, Оизм, Rизм - измеренные радионавигационные параметры (скорость, азимут и дальность, соответственно); V, О, R - истинные радионавигационные параметры; А1, А2, А3 - аппаратные функции.

С учетом ошибок, которые возникают при измерении сигнала, уравнение (6) примет вид

• V    = А ^_И зм + А V ;

• * О = А ₂1 О изм +АО ;                                                                               (7)

_ R = А 3 ^{- 1} R изм +A R .

Если принять, что модель прохождения радиосигнала описывается одномерным интегральным уравнением Фредгольма первого рода типа свертки

J A ( x - S ) y ( S ) ds = f ( x ),                                                                         (8)

-J где f(x) – измеренное значение сигнала; y(x) – истинное значение сигнала; A(x–s) – аппаратная функция, тогда решение (8) по методу регуляризации Тихонова будет иметь вид [1]

1 J ^ аист ⁽ x )   ~ I

2 n

-J

А 1 ( -0 ) V изм ( 0 )

e ^- j ^{to x}d rn ;

| A 1 ( -to)| + а|ю|² p

^^          ^^

А 2 ^{( -}® > ^О измИ

J

^О а ист ^{( x} ) ~ I ,„          ,2      . ,

2 ⁿ , | А ₂ ( -to)| + a|to|

2 p

e ^- j ^to x d to ;

1 ^{J R} а ист ^{( x} ) =      I

2 n

-J

A3(-to) ^змИ |A3(-to)|2 +a|to|2 p e - j toxd to,

где V a ист ( x ), О а ист ( x ), R а ист ( x ) — приближенное истинное значение; ^( to ), О_Ю мИ , _JR изм ( to ) — Фурье-образы У и _{з м}( x ), О _изм( x ), R _изм( x ); A 1 ( -to ), А ₂ ( -to ), А ₂ ( -to ) - Фурье-образы аппаратных функций; a , p - параметры регуляризации.

Второй подход предполагает определение параметров V , О , R любым известным методом (методом Андерсона, Фроста, методами адаптации [7] и т. д.), при этом вместо аппаратной функции будет использоваться некоторая модель, ее замещающая

N

f ⁽ x ) = ^ A ( x , x -) y , ( x ) + § f ,                                                                    ⁽⁹⁾

i = 1

где x - параметр обработки (угол, скорость и т. д.); A ( x , x i ) - некоторая модель, замещающая аппаратную функцию.

В этом случае получается система линейных алгебраических уравнений, которую можно решать обобщенными методами редукции с использованием методов регуляризации [1].

Третий подход предполагает определение параметров V , О , R , выполняя обработку сигналов с использованием критерия максимального правдоподобия [5, 6]. В итоге задача сводятся к интегральным уравнениям Фредгольма первого рода, которые решают с помощью методов регуляризации.

В качестве примера решения некорректной задачи можно привести задачу вычисления преобразования Фурье:

• Y ( to ) = J y ( t ) e^{1 to} t dt , - j <  t <  j;                                                                    (10)

  -J

1 J

y ( t ) = — [ Y ( to ) e^{1 to} t dt , -j,

2n J

-J где Y(ю) - прямое непрерывное преобразование Фурье, а y(t) - обратное непрерывное преобразование Фурье.

Пусть имеется функция, для которой необходимо выполнять прямое преобразование Фурье по формуле (10)

, . sin( ю tt ) У ( t ) =     —

.

tozt

Подставив в (10), получим следующее y (ю).(11 t) e-tdt.

ю_ t

-да z

Решая аналитически (13), находят спектр функции (12)

—, юе(-ю z, ю z); ю z IY (»)| = <

• 0, ю^(-ю z, ю z);

n----, ю = ±ю_.

2 ю _z        ^z

Преобразование Фурье является некорректной (неустойчивой) задачей, так как связана с уравнением Фредгольма первого рода, хотя неустойчивость несколько сглаживается, потому что это уравнение решается аналитически.

В [8] приводится вывод регуляризированной формулы для нахождения преобразования Фурье на основе метода регуляризации Тихонова.

В общем виде формула имеет вид:

да

Ya (Ю) = J

-да

где f ( t , a ) =

y ( t )

1 + a t ^{2 n}

e ^ю t dt ,

1 + a t ² n

– стабилизирующий

коэффициент, подавляющий высокие частоты [8];

a , n - параметры регуляризации.

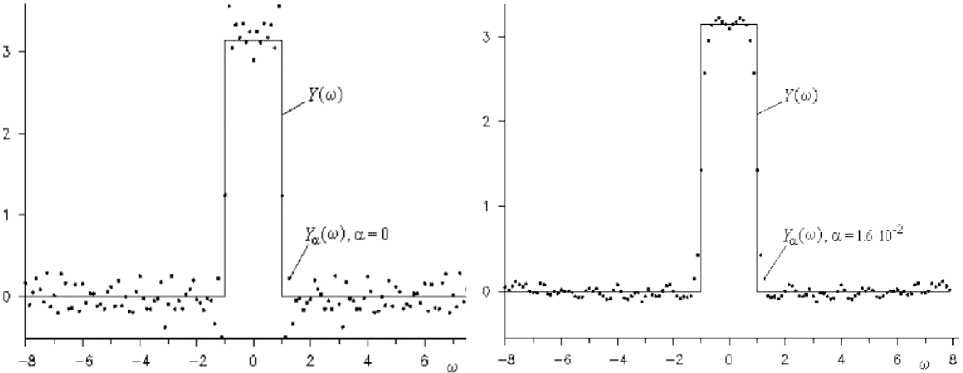
а)

б)

Выполнение преобразования Фурье (а) и его регуляризация (б)

Из рис. 1, а видно, что вместо Y(ю) в виде прямоугольника получается окно с осцилляциями Ya (ю). И при a = 0 (без регуляризации) возникает эффект Гиббса. Если использовать регуляри-зированную формулу Ya (ю) при a = 1,6 • 10-2, то подавляются те отсчеты, которые вносят наибольшие погрешности, и уменьшается погрешность вычислений (1, б). Таким образом, регуляри- зация уменьшает погрешность вычисления Y(ю) (а значит, увеличивается соотношение сиг-нал/шум) в 2-3 раза. Причина этого в том, что слагаемое a- tk в (14) подавляет умеренно дальние отсчеты в y(t), чьи погрешности вносит наибольший вклад Ya (ю). Метод регуляризации Тихонова является идейным продолжением метода наименьших квадратов (дающий псевдорешение) и метода псевдообратной матрицы Мура–Пенроуза (дающий нормальное решение).

Метод регуляризации Тихонова решается посредством неопределенных множителей Лагранжа:

II Ay - fIII 2 + alЫt = min,                                                                  (15)

где a >  0 - параметр регуляризации, играющий роль неопределенного множителя Лагранжа. Если a = 0, то метод переходит в метод наименьших квадратов с малой невязкой || Ay - f || и большой неустойчивостью. С увеличением α решение становится более гладким, но невязка увеличивается. Поэтому подбирая α, можно приблизиться к приемлемой невязке, и решение будет приемлемо устойчивым.

Из (15) вытекает

(a E + А Т А ) y a = А Т f ,                                                               ⁽¹⁶⁾

где E – единичный оператор, A^Т – транспонированная матрица.

Существует способы подбора α, три из которых представлены в [1].

В более общем виде метод регуляризации Тихонова можно записать:

и Ay -f С+ai ly -^iL = mn,                                                     <17)

где v — математическое ожидание или начальное приближение.

Функция (17) применяется для регуляризации некорректных задач редко из-за неопределенности v , однако на основе (17) можно детальнее проследить схожесть с методом оптимальной фильтрации Калмана.

Применительно к интегральному уравнению Фредгольма I рода b

Ay = j K ( x , s ) y ( s ) ds = f ( x ), c <  x <  d , a

• (16)    приобретает вид b

a y a ( t ) + j R ( t , s ) y a ( s ) ds = F ( t ), a <  t <  b ,

a где

d

R ( t , s ) = R ( s , t ) = j K ( x , t ) K ( x , s ) dx ;

c

d

F ( t ) = j K ( x , t ) f ( x ) dx .

c

Для уравнения Фредгольма I рода типа свертки

w j K(x - s)y(s)ds = f (x), - w< x

-w решение можно найти с помощью метода преобразований Фурье и затем регуляризировать найденное решение.

Исходя из [1], аналитическое решение (18) примет вид обратного преобразования Фурье

”

y (s) = — Jy (to)e-^{iю s}d ю,

2n

-w где

∞

Y(ω)=

F(ω) λ(ω)

∫ f (x)e^iωxdx

-∞

∞

∫ K(x)e^iωxdx

-∞

Регуляризированное решение находится из условия минимума сглаживающего функционала (17)

∞∞

∫ [Ay - f (x)]²dx + α ∫ M(ω) I Y(ω)I²dx = min,

-∞                  -∞                   y где M(ω) = Iω I λq, где q ≥ 0.

Из (19) получается регуляризированное решение y (s)=∞ λ(-ω)F(ω) e α    -∫∞ L(ω) + αM (ω)

-

iωsdω,

где L(ω) = Iλ(ω) ² .

При выборе q следует учесть, что чем больше это значение, тем сильнее подавляются высокие гармоники, а при выборе параметра регуляризации α использовать уже существующие алгоритмы, такие как метод невязки, метод подбора и т. д.

Метод регуляризации Тихонова является идеальным инструментом для нахождения квазиу-стойчивого решения некорректных задач с точки зрения сложности алгоритмов и точности. Также он не требует большого количества априорных сведений (только значения погрешностей и иногда математическое ожидание ψ), в отличие от метода оптимальной фильтрации Калмана – Бьюси. Поэтому фильтр Калмана относят к методам статистической регуляризации наравне с фильтром Винера. Оптимальный фильтр Калмана требует априорное знание о ковариации ошибок, а также матожидания правых частей.

Таким образом, если существует физическая задача, то ее необходимо свести к интегральному уравнению Фредгольма, затем решать ее с помощью методов регуляризации.

Выводы

Подводя итог, можно сказать, что решение прикладных задач как некорректных задач интересно, в первую очередь, своей оригинальностью. Несмотря на то, что об обратных задачах (некорректных задачах) знают уже больше ста лет, практическое применение они находят только с недавнего времени с открытием способа устойчивого решения с применением методов регуляризации.

На сегодняшний день, когда вычислительная мощность процессоров не ограничивает конструкторов в разработке сложных алгоритмов, необходимо усовершенствовать методы регуляризации и искать новые подходы для улучшения качества обработки сигналов, изображений и т. д. Поэтому необходимость применения обратных задач для обработки сигналов в радионавигации наряду с классическими методами авторы представленной статьи считают обоснованной и актуальной.

Поскольку статья носит постановочный характер, определение конкретных алгоритмов для некорректных задач навигации с применением регуляризации будет представлено в последующем исследовании.