Обратная задача дифракции электромагнитной волны на плоском слое

Рассмотрим дифракцию электромагнитной волны на плоском слое. Слой имеет пренебрежимо малую толщину и полностью описывается своей функцией пропускания. Требуется подобрать такую функцию пропускания, чтобы создаваемое в плоскости регистрации изображение обладало заданными свойствами. Соответствующая оптическая схема показана на рис. 1 . Такая задача возникает во многих практических приложениях, например, в задаче создания голографических изображений [1] .

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-31-60096 мол-а-дк.

(О Д. Ю. Князьков, 2018

(О Институт проблем механики им. А.Ю. Ишлинского РАН, 2018

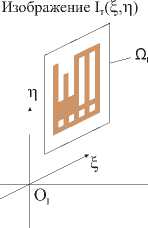
Плоский слой T(x,y)

Ω

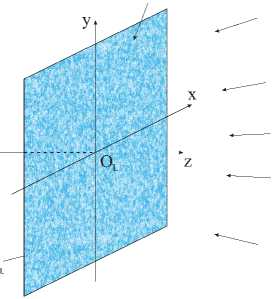
Поле W(x,y)

Рис. 1. Схема падения волны на плоский слой

Сформулированная выше обратная задача требует больших вычислительных мощностей, так как даже прямая задача моделирования освещения дифракционной пластины электромагнитной волной сводится к расчету, требующему порядка O(N 4 ) операций, где N — характерное количество точек в вычислительной сетке на пластине или на изображении [2] . Специально разработанный алгоритм большого пикселя, позволяющий снизить количество требуемых операций до CN 2 logN с достаточно маленькой константой C , был предложен в [3] . Этот алгоритм был реализован в виде высокопроизводительной суперкомпьютерной программы. Он основан на использовании аналитического решения задачи дифракции на квадратном отверстии и быстрого преобразования Фурье. Эффективность последнего при дополнительных, накладываемых алгоритмом метода требованиях была исследована на кластерах HybriLIT и МВС-100К в [4] .

Задача оптимизации качества изображения в рассматриваемой оптической схеме методом локальных вариаций ранее решалась в [5]. Было показано, что возможно существенное улучшение качества изображения. Основным недостатком этого метода были высокие требования к вычислительным ресурсам: на каждый шаг процесса оптимизации требовалось время, равное времени двух полных восстановлений изображения с дифракционной пластинки. В настоящей статье предлагается использовать градиентный метод, что должно снизить количество требуемых операций. Преимущество здесь может быть не только в использовании большего шага в ходе итерации, но и в возможности использовать упомянутый выше метод большого пикселя в процессе вычисления градиента.

Описанный выше подход к моделированию распространения излучения предполагает использование скалярной модели дифракции Кирхгофа в дальней зоне. Более тонкий анализ прохождения электромагнитной волны через дифракционную пластину ненулевой толщины может быть выполнен с помощью метода, предложенного в [6] для цилиндрического слоя и H-поляризованной [7] или E-поляризованной [8] волны. Этот метод также может быть использован в существенно трёхмерной постановке для моделирования дифракции плоской электромагнитной волны на периодическом в двух направлениях неоднородном слое ненулевой толщины.

• 2.    Постановка задачи

Пусть электромагнитная волна W (x,y) падает с положительного направления оси Oz на слой, лежащий в области Q l в плоскости Oxy . Считается, что слой имеет пренебрежимо малую толщину, а его пропускание задается функцией

T(x,y):^L ^ [0,1], где области {(x, y)|T(x, y) = 1} полностью прозрачны для излучения, а через области {(x, y)|T(x,y) = 0} свет не проходит. В результате дифракции электромагнитной волны на этом слое, в плоскости Oξη, находящейся на расстоянии d от Oxy , формируется изображение с интенсивностью, задаваемой функцией IT(£, п).

В скалярном приближении интенсивность изображения, формируемого при засветки слоя T волной W , может быть в дальней зоне дифракции рассчитана с использованием интеграла Кирхгофа [9] :

I T

(м= и

к(x, y, ^, nW(x, y)T(x, y)dxdy

Ω L

Требуется найти такую функцию пропускания слоя, чтобы в области ^i создать изображение qoK,n) :^I ^{0, 1}.

Желаемое изображение — это набор геометрических объектов с около-волновыми и субволновыми размерами. Таким образом, необходимо найти такую функцию T(x, y), что

УУ K(x,y,£,nW(x,y)T(x,y)dxdy

= q o (€,n).

Ω L

Функция q o (^,n) кусочно-постоянная (принимает только значения 0 и 1), поэтому точного решения задачи (1) не существует. Будем искать ее квазирешение [10] из условия

Р (qoUMI T ⁽^пТ) -> min .

В качестве меры отличия получающегося изображения I(£,п) от заданного q o (^,n) выбрана нормализованная средняя абсолютная ошибка

Р Ш; -V (•, •)) = УУ

Ω I

qoU,n) ^-

I (е,п) max I (£,п) Ω _I

dξdη,

Нормализацию функций отличия изображений целесообразно применять в случае, когда умножение на вещественную константу не должно менять значение отличия [11] , например, такой выбор меры ошибки используется в приложениях, связанных с моделированием восприятия изображения глазом человека, в задачах сжатия таких, предназначенных для человека, компьютерных изображений [12, 13] , в задачах литографии при моделировании процесса засветки фоторезиста. В первом случае отличия в интенсивности будут нивелированы в ходе дальнейшей обработки изображения зрительной системой, во втором — продолжительностью экспонирования светочувствительного материала.

• 3.    Оптимизация качества изображения градиентным методом

Пусть область, занятая слоем Q l — квадрат, и этот квадрат разбит на N ² одинаковых ячеек □ i , i = 1,..., N ² . Решение (2) будем искать на множестве G 1 кусочно постоянных на этих ячейках функций: G 1 = {T(x,y) | T(x,y) = const = t i , (x,y) e □ i }. Интенсивность излучения в плоскости изображения в точке (£, n), создаваемая слоем T(x, y) e G 1 при освещении ее волной W равна

УУ K (x^,y^,^^,n ^{) W ( x,}y ^{) T} (^x,y ^{) dx}dy

Ω L

N ²

= 5 t i и K«

— x,n - y)W(x, y)dxdy

□ i

N ²

5 t i F i (^,n)

i = 1, ...,N2.

Интегралы

F i ( x, y ) =

□ i

K К - ^x,n - y^)W(x, y^)dxdy

k γ ²

при 02 ^ 1, где y - размер ячейки, а k o - модуль волнового вектора, могут быть вычислены аналитически в приближении дальней зоны [14] . В качестве области Q i возьмем квадрат, который разобьем на равномерную сетку с M ² узлами (^ i , n m ), l,m = 1,..., M.

Тогда для нормы (3) целевая функция

M

J (T) = 5

l,m =1

q o ⁽6,nm) ^—

N ²

E t i F i (^ l ,n m )

i =1

max n,p

N ^{2               2}

E t i F i (€ n ,n p )

где T = {t i , ...,t N 2 } - коэффициенты пропускания соответствующих ячеек на слое:

• (5)                       0 <  t i < 1, i = 1,...,N ² .

Будем решать задачу оптимизации в R ^N

• (6)                        J (t ₁ ,...,t _N 2) ----------- У min

{t1,...,tN2 } для целевой функции (4) при ограничениях (5). Вообще говоря, эта задача не эквивалента исходной, но её можно рассматривать как регуляризацию (2) на основе дополнительной информации о поведении функции T(x,y), например, о плавности ее изменения, продиктованной особенностями физической реализации дифракционного слоя и необходимостью не выйти за рамки рассматриваемой скалярной модели распространения излучения. Поскольку задача (6), (5) ставится на компакте в RN2 , ее решение будет существовать, и оно будет решением задачи (2) на множестве функций G1.

Будем искать решение задачи (6) , (5) с помощью метода градиентного спуска. На (k + 1)-ой итерации этого метода

• ^• происходит движение по антиградиенту целевой функции с постоянным шагом α :

Г dj (T k )      dj (T k ) ;

• ⁽⁷⁾               T ^{k +1}    T k ^at dt i ’•••’ dt N 2 j’

• • вычисляется значение целевой функции в новой точке T k +₁ :

• (8)                  j (T k +i ) = j (t k ⁺ⁱ,t k ⁺ⁱ,...,t N +^v ).

Итерационный процесс завершается, если достигнута требуемая точность поиска δ :

|J (T k +1 ) - j (T k )| <5,

либо если сделано максимально допустимое количество шагов k max :

k + 1 = k

max .

В качестве решения T _opt берется последняя рассчитанная функция пропускания слоя:

T opt

= T k +1 .

В качестве начального приближения будем использовать функцию

T o

y //

Ki К, n, x, y)q o ⁽^, n^)R(^, nWdn + W ⁽x, y)

Q i

представляющую собой функцию прозрачности амплитудной голограммы Габора [15] , то есть результат интерференции по дс веченного волной R(^/q) заданного изображения q o (^,n) и волны W(x,y), сопряженной к исходной волне W(x,y). В результате освещения слоя с такой функцией пропускания T o (x,y), в плоскости изображения O^n будет сформировано изображение, достаточно близкое к требуемому q o (^,n) [16] .

• 3.1.    Параллельная реализация алгоритма

dJ ( T_k )

Для численного вычисления компоненты ∂t k градиента используется формула k      k k      k        k        k      k kk        k

J ^{( t} 1 , . . . , t j - 1 , t j ⁺ , t j +1 , ■ ■ ■ , t N 2 ) J ^{( t} 1 , . . . , t j - 1 , t j , t j +1 , . . . , t N 2 )

h.

Обозначим комплексные значения поля в точках (^ i ,n m ) изображения

N ²

• (11)          E k (l,m) = ^ t ^k F i (^ i ,nm), l,m =1,...,M.

i =1

Тогда значение целевой функции J(T k ) рассчитывается следующим образом:

M j (Tk )= E l,m=1

q o (^ l ,n m)

|E k (l,m)\ 2 max \E _k (n, s) \ ² n,s

Таким образом, для расчета производной (10) необходимо еще знать

N ²

• (13)    E j (l,m) = E t k F i (^ i ,П т )+ hF j (^ 1 ,П т ), l,m = 1,...,M.

Таблица 1. Затраты при параллельном вычислении поля

количество ядер кластера МВС-100К	16	32
время одной итерации в секундах	801	1004
время расчета J (T ) в секундах	97	46

Комплексное изображение (11) хранится в течение расчета всех ^{dJ (}T ^k ) , j = 1,..., N ² , а после определения градиента и следующего приближения T k +i в соответствии с (7) , новое комплексное изображение E k +i (l,m) рассчитывается и используется как для расчета текущего значения целевой функции (8) , так и на (к + 1)-ой итерации для расчета ^dJ (T^ ¹ ) , j = 1,..., N ² .

∂t j

Формулы (11) и (13) отличаются только слагаемым F j (^ i ,n m )• Пусть для расчета используется N _p расчетных ядер. При подсчете частных производных (10) можно параллельно рассчитывать свой набор MN- значений интеграла F j (^ l , n m ) на каждом из вычислительных ядер. Такой способ распараллеливания был реализован ранее для расчета результата дифракции на плоском слое [2 , 17] и показал близкую к 1 параллельную эффективность. Более того, такой метод использовался в настоящей работе для подсчета (8) по формулам (11) , (12) . Однако такой подход оказался неэффективным при расчете градиента.

В таблице 1 показан пример изменения полного времени одной итерации и времени расчета значения целевой функции (8) при удвоении количества используемых вычислительных ядер. (Расчет целевой функции (8) по известным комплексным значениям поля в плоскости изображения требует лишь O(N ² ) операций, поэтому время расчета (8) практически не отличается от времени расчета комплексного поля (11) .)

Видно, что время расчета целевой функции падает примерно в два раза, в то время как время расчета градиента существенно превышает время расчета целевой функции, и оно не только не уменьшается, но даже растет с увеличением количества ядер. Это связано с тем, что расчет F j (^ l ,n m ) соответствует расчету дифракционного интеграла не по всей площади слоя, а только по j -ой ячейке, из-за чего увеличивается

Таблица 2. Затраты в секундах при параллельном вычислении градиента

кластер HybriLIT МВС-100К количество ядер 6 12 24 16 24 32 время одной итерации 412 209 102 182 119 93 время расчета J(T) 176 94 46 92 58 47 доля накладных расходов на межпроцессорный обмен, что ведет к такому резкому падению эффективности параллельных расчетов при увеличении Np .

Поэтому для расчета градиента был реализован следующий алгоритм параллельного расчета. Расчет F j (^ i , n m ), l,m = 1,..., M 2 осуществляется целиком на одном вычислительном ядре, при этом расчет всех компонент градиента ведется параллельно. Каждый n-ый процесс, n = 1,...,N p рассчитывает компоненты градиента 22

с j n = N" ( n — 1) по з П = N" n, для чего осуществляется расчет соответствующих F j (^ i ,n m ), j = j n ,...,j n .

Таким образом, за время расчета градиента расчитывается N ² интегралов F j (^ i ,n m ), значит сложность такого расчета эквивалентна расчету комплексного изображения (11) . Поэтому вычислительная сложность одной итерации оптимизационного процесса должна быть в два раза больше времени расчета комплексного изображения (11) .

Такой способ параллельной организации вычислений был реализован в программе на языке программирования С++. Расчеты с помощью этой программы выполнялись на кластерах HybriLIT ЛИТ ОИЯИ и МВС-100К МСЦ РАН. Полное время выполнения одной итерации и время расчёта значения целевой функции J(T ) показаны в таблице 2 . Видно, что теперь эффективность работы программы близка к 1 (ускорение почти линейно), а время одной итерации оптимизации действительно соответствует времени двух полных расчетов результата дифракции электромагнитного поля на всем слое.

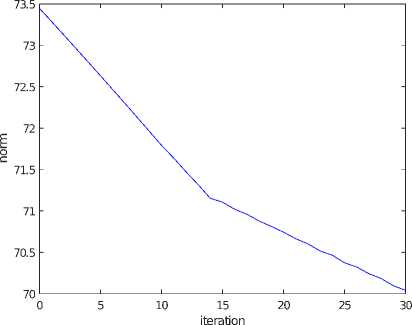
Рис. 2. Уменьшение значения целевой функции на в ходе итераций градиентного метода

• 3.1.1. Пример оптимизации градиентным методом

  Пример хода оптимизации градиентным методом показан на рис. 2. Здесь размеры расчетных сеток N = 638, M = 120, то есть дифракционный слой состоял примерно из 407 тысяч элементов, а изображение — примерно из 14 тысяч расчетных элементов. Всего было сделано 30 шагов итерационного процесса. При этом норма отличия изображения от заданного уменьшилась с 73.4 до 70.0. Параметр условия остановки (9) алгоритма δ = 0.06, а значение нормы на последних итерациях было равно J (T 29 ) = 70.0972, J (T 30 ) = 70.0391, то есть различие составило |J (T 30 ) - J (T 29 )| = 0, 0581. Весь процесс оптимизации занял 29 минут на 32 вычислительных ядрах суперкомпьютера МВС-100К.

• 3.2.    Аналитическое вычисление градиента

Таким образом, градиентный метод оптимизации позволяет достичь улучшения качества изображения подобного улучшению, полученному ранее с помощью метода локальных вариаций [5]. При этом качество изображения существенно улучшается: например, примерно с 15 до 5 процентов уменьшается всплеск интенсивности на границе ярких и тёмных областей изображения. Этот всплеск интенсивности объясняется эффектом Гиббса — неравномерностью сходимости частичных сумм ряда Фурье функции вблизи ее точки разрыва первого рода. В нашем случае подобный эффект проявляется, так как мы пытаемся сформировать оптическое изображение, яркость которого задается разрывной функцией qo(£,n).

Нет никаких оснований считать, что получаемая в ходе описанного выше оптимизационного процесса функция пропускания слоя T _opt является точкой минимума функции (4) либо решением (квазирешением) исходной задачи (1) . Так, например, применение к результату градиентной оптимизации T _op_t метода локальных вариации [5] либо наоборот (к результату метода локальных вариаций — метода градиентного спуска) позволяет несколько уменьшить значение функционала отличия (3) .

Целевая функция (4) имеет достаточно сложную структуру. Она не принадлежит, например, к классу квадратичных выпуклых функцией, для которых применение градиентных методов оптимизации позволяет достаточно эффективно решать задачу поиска глобального минимума. Однако, метод градиентного спуска позволяет получить требуемое качество результирующего изображения с одной стороны и обладает, как было показано, высокой параллельной эффективностью на кластерных вычислительных системах, что позволяет использовать его для оптимизации изображений, получаемых с дифракционных пластин, если только сложность изображения не слишком велика.

Если же требуемое изображение состоит из большого количества элементов (M, N = 10 4 и более), то описанный подход будет не применим из-за высокой (порядка O(N 4 )) сложности расчета компонент градиента по формуле (13) . В этом случае, например, для нормы р = L 2 , вариация соответствующего функционала

2 ²

J 2 ^{(T )} I ■ " //

Qi        Ql

K (х,уЛ,пЖ(x,y)T (x,y)dxdy d^dn может быть получена аналитически:

• (14)                 6^J 2 ^(T ) = 4Re ⁽ V ^(x,y'^),5T⁽x,y'⁾'⁾ ( x,y ) ,

где

K * T - K * T • q o ² ] U,nWdn,

V(x,y) = y[ K1 (х-^У-П) [|K * T|2 • здесь K ∗ g обозначает свертку

I IK К - x,n - y)g(x, y)dxdy.

Ω L

То есть расчет (14) может быть сведен к расчету четырех сверток типа (15) . Такой расчет может быть выполнен уже с использованием CN ² log(N) операций [3, 4] , что делает возможной оптимизацию изображений, состоящих из большого количества элементов на современных суперкомпьютерах кластерного типа.

• 4. Заключение

Была рассмотрена обратная задача синтеза функции пропускания плоского дифракционного слоя по формируемому им при освещении электромагнитной волной изображению. Для решения задачи применялся градиентный метод. На языке программирования С++ была реализована параллельная версия алгоритма этого метода, были исследованы результаты еe работы и еe эффективность. Хотя метод градиентного спуска не позволяет найти глобальный экстремум в решаемой задаче, с его помощью удается добиться требуемого улучшения качества изображения, а параллельная эффективность соответствующей программы близка к единице. Таким образом, качество результата и эффективность оптимизации оказалась близка к результатам оптимизации методом локальных вариаций, реализованному ранее.

Описан подход численно-аналитического расчета градиента, позволяющий, с использованием специального метода расчета результата дифракции волны в дальней зоне, реализовать метод градиентного спуска для слоя состоящего из 10 8 и более элементов пропускания.

Представляет интерес реализация описанного выше метода градиентной оптимизации для изображений сложной структуры, а также применение использованного в настоящей работе подхода к решению обратной задачи дифракции электромагнитной волны на неоднородном слое ненулевой, конечной толщины.

Работа выполнена с использованием вычислительных ресурсов Межведомственного суперкомпьютерного центра Российской академии наук (МСЦ РАН): часть расчетов проводилась на высокопроизводительной системе МВС-100К.

Автор выражают глубокую признательность руководству и сотрудникам ЛИТ ОИЯИ, любезно предоставившим возможность и техническую поддержку расчетов на кластере HybriLIT.