Обратная задача определения диаграммы деформирования материала по диаграмме чистого изгиба балки

В механике деформируемого твердого тела существует проблема достоверного экспериментального определения свойств материала на всех стадиях его деформирования и особенно на закритической стадии. Непременное условие эксперимента состоит в сохранении образцом однородного напряженно-деформированного состояния, что не всегда удается осуществить. Например, при растяжении стандартного образца из пластичного материала появляется так называемая шейка, и напряженное состояние становится трехмерным.

Одним из возможных путей решения этой проблемы является проведение испытаний специальных конструктивных элементов по специальной программе с последующим пересчетом данных эксперимента на свойства материала.

Такие задачи определения количественных характеристик явления по результатам измерений их косвенных проявлений представляют так называемые обратные задачи, часто возникающие в физике, технике и других отраслях знаний. Как правило, они относятся к классу некорректных задач [1,2].

В данной работе рассматривается конструктивный элемент в виде балки прямоугольного сечения и решается обратная задача определения свойств материала по экспериментальным результатам, полученным при чистом изгибе.

Некорректная задача и метод регуляризации [1]

Пусть изучаемый объект характеризуется элементом z_T, принадлежащим множеству F. Часто z_T недоступен для прямого изучения, и исследуется некоторое его проявление Az_T = и_т(и_те AF, где AF - образ множества F при отображении, осуществляемом оператором А). Очевидно, что уравнение

Az = и                                 (1)

имеет решение на F только для таких элементов и, которые принадлежат множеству AF . Элемент и обычно получается путем измерений и потому известен приближенно.

Пусть и_д - приближенное значение. В этих случаях речь может идти лишь о нахождении приближенного к г_т решения уравнения

Лз = ид                               (2)

При этом Мд, вообще говоря, не принадлежит множеству AF . Оператор А во многих случаях таков, что обратный ему оператор А”' не является непрерывным. Например, оператор А представляет собой интегральный оператор. В этих условиях нельзя в качестве приближенного решения брать точное решение уравнения (1) с приближенной правой частью, то есть нельзя в качестве приближенного решения брать элемент z=A⁴u^ так как, во-первых, такого решения может не существовать на множестве F , поскольку м_д может не принадлежать множеству AF (не выполняется первое условие корректности по Адамару), во-вторых, такое решение, даже если оно существует, не будет обладать свойством устойчивости, поскольку обратный оператор не является непрерывным (не выполняется третье условие корректности).

Возможность определения приближенных решений некорректно поставленных задач, устойчивых к малым изменениям исходных данных, основывается на использовании дополнительной информации относительно решения. Широко распространенным в вычислительной практике способом приближенного решения уравнения (2) является метод подбора. Он состоит в том, что для элементов г некоторого заранее заданного подкласса возможных решений Вер вычисляется оператор Az, то есть решается прямая задача. В качестве приближенного решения берется такой элемент z₀ с В , на котором невязка p^Az^u^ достигает минимума, т.е.

zeS

Здесь р^А2_Ъзи^ - расстояние между элементами Az₀ и и_д в некоторой метрике.

Уравнение чистого изгиба

Рассмотрим чистый изгиб имеющего высоту h и ширину b .

балки прямоугольного поперечного сечения,

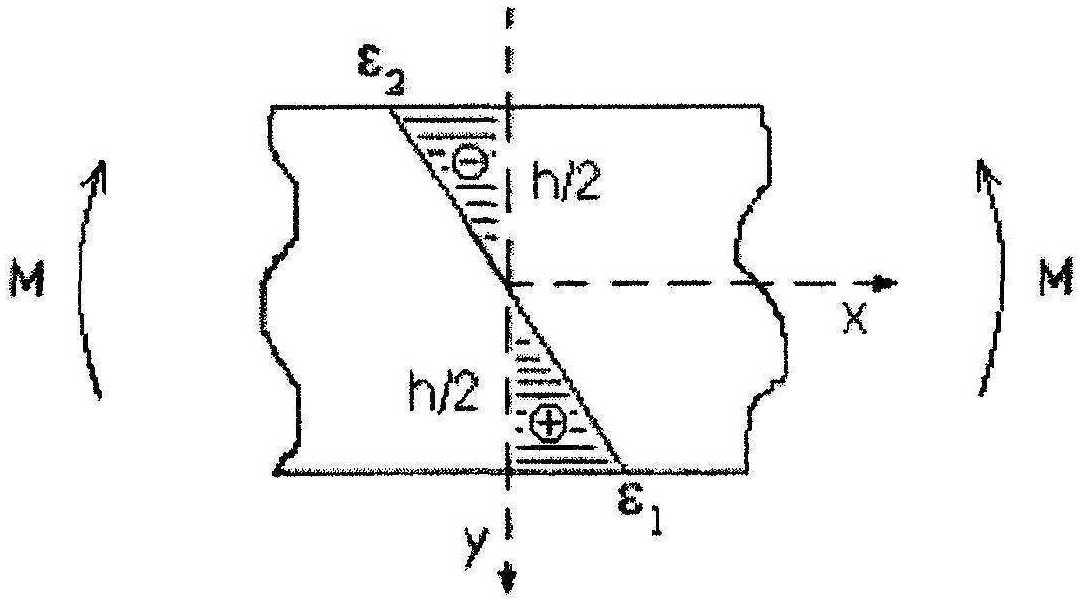
Рис.Г Распределение деформаций

В этом случае единственной ненулевой компонентой тензора напряжений будет продольное напряжение ах=а, а продольная деформация ^=^ линейно распределена по высоте балки (рис.1). Полагаем, что зависимость напряжений от деформаций <т(£) одинакова для растяжения и сжатия. Тогда нейтральная линия не меняет своего положения при изгибе и проходит посередине балки, совпадая с осью Ох (рисЛ). Отсюда ^=/^/2, е2=-кЬ/2, где к - кривизна балки, ev £2 " деформации наиболее растянутых и сжатых волокон.

Уравнение чистого изгиба, связывающее изгибающий момент М и кривизну балки, имеет вид [3]

хА/2

2b f A^^ds = М<к^.

о

Если известна зависимость а^Е ), то выражение (3) определяет зависимость М^ (прямая задача). Когда по известной функции М^ необходимо найти функцию <г(£) (обратная задача), то уравнение (3) представляет собой интегральное уравнение Вольтерра первого рода.

Алгоритм решения обратной задачи

Пусть зависимость М^ получена в эксперименте. Это может быть набор точек ^Мк,кк^, либо записанная с помощью какой-либо аппаратуры некоторая непрерывная кривая, которая, вообще говоря, может иметь и угловые точки. В любом случае в дальнейшем будем иметь дело с набором точек (Мк,к*к), полученным с точностью, позволяемой экспериментальной аппаратурой.

Возьмем две точки, расположенные рядом (М^к,), (Мм ,кгм). Используя формулу (3), находим м .-2 к:мМ1      ^2.        ^/2

—‘-.....— = ^Ety(f)d£= J Ea^dEA- ^EO^dE ,

О          0           ^/2

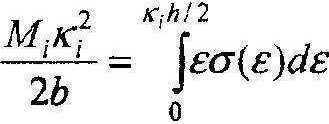
Вычитая из первого выражения второе, получаем равенство

ДО

^jA/2

- М^^ = ^£C7(f)d£ к^И

Полагаем, что зависимость <т(е) на отрезке \_Kihl2sicMhl2"\ линейна с углом наклона оц, а именно, о = а^ + tg а-(е -£,-), где tg af -Ef, t^^h/2. Здесь Ер- касательный модуль, который на стадии упругости равен модулю Юнга Е. Подставляя данное выражение для а в правую часть формулы (4) и производя необходимые действия и преобразования, находим

_ЕР ₌ з (^,41^1 - М^Ъ - 5(41 - ^)                   ₍₅₎

'       Ж^л-Зк^+ХА-К^ ■

Затем получаем а = <у^ ЕР (Kv^h/2 -^h/2),                      (6)

где к:_мИ/2 = £_i+x, ^Ь/2 = Е,.

Начиная процесс вычислений с первой точки, где М_А = 0, к_х =0, ст, =0, по формулам (5), (6) последовательно рассчитываем значения бг. и ^, по которым восстанавливаем диаграмму деформирования материала сг(е).

Пример

Решим сначала прямую задачу для балки высотой h = 2 мм и шириной b = 1 мм . Свойства материала пусть заданы зависимостью (вставка на рис.2)

£е,

0 <е<0,003;

аг(е) =

60 + Е^ (£ - 0,003), 0,003 < £ < 0,006;

90 + Е^_ (е - 0,006), °. 006 < Е < 0,009;

где£ = 2-10⁴ кг/мм², Е^ = 1 • 10⁴ кг/мм², Е^ = ~3• 10⁴ кг/мм². По формуле (3) вычисляем

— 104к,

3                      0<к<0,003;

М_т (к) = *

30 + -Л04к-9 10'5к"2,   0,003 < к <0,006;

d              9 0,006<к<0,009;

270-2-104k-297-10~5k ,

Зависимость М_т^ изображена на рис.2, кривая 1.

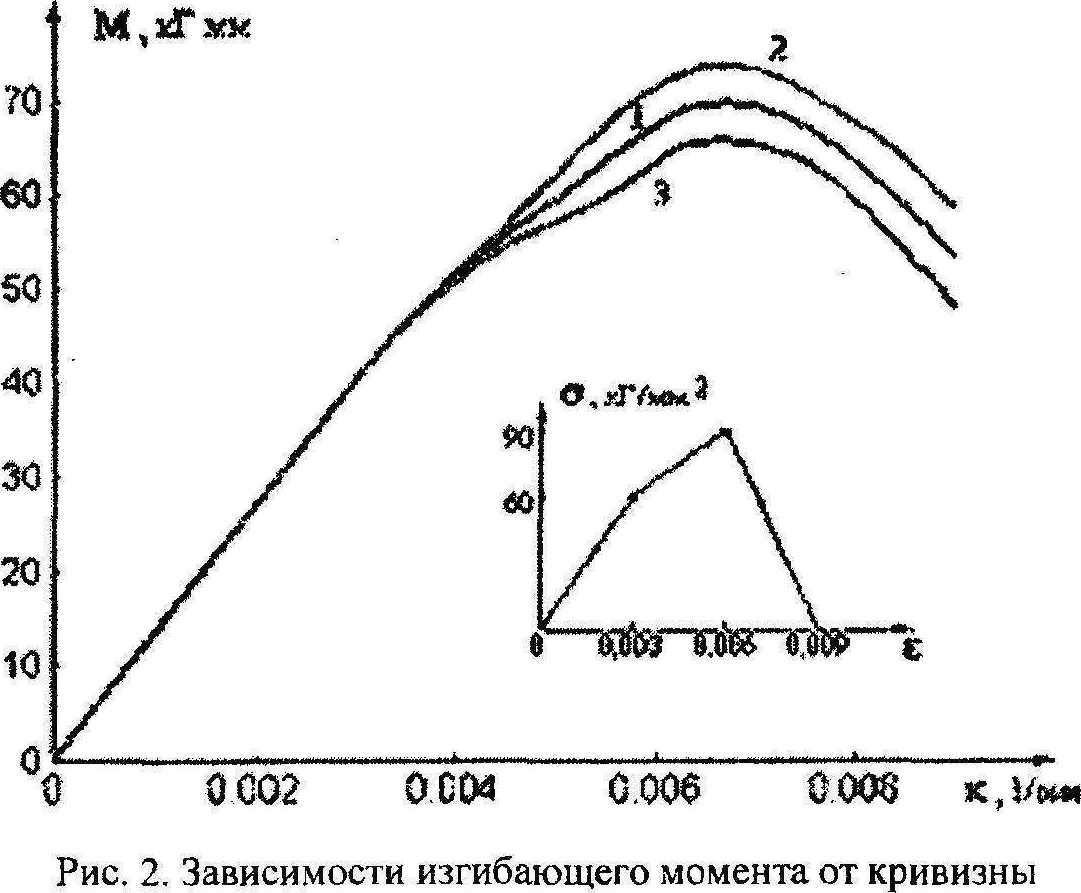
Решим теперь обратную задачу, используя формулы (5), (6). Для этого из выражений (7) получим набор значений (М^к^ с шагом по к, равным 0,0001. Если величины M_t брать с точностью до шести знаков, то из расчета по формулам (5), (6) получаем практически точную диаграмму <г(е) = <7_т(е).

Пусть измерение зависимости М^ осуществляется в эксперименте приближенно. Моделируя данную ситуацию, оставим в значениях M_t только один знак после запятой. Пересчет приближенной функции М_д(/г) в диаграмму сг^Е) дает характерную пилообразную кривую (см. рис.З). Таким образом, уравнение (3) с интегральным оператором Вольтерра является некорректным, и для нахождения приближенного решения следует применить какой-либо метод регуляризации.

Проведем через верхние и нижние точки пилообразной ломаной линии кривые 2 и 3 (см. рис.З). Используя их при расчете изгибающего момента, получим кривые 2 и 3 (см. рис.2), лежащие соответственно выше и ниже экспериментальной кривой М^^.

Для определения приближенной зависимости (7(f) применим метод подбора. В данном случае подкласс возможных решений В составляют функции o*_k(s), графики которых расположены между кривыми 2 и 3 (см. рис.З). Решая прямую задачу для всевозможных таких функций, получаем зависимости M_k (f), графики которых лежат между кривыми 2 и 3 на рис.2. Тогда невязка

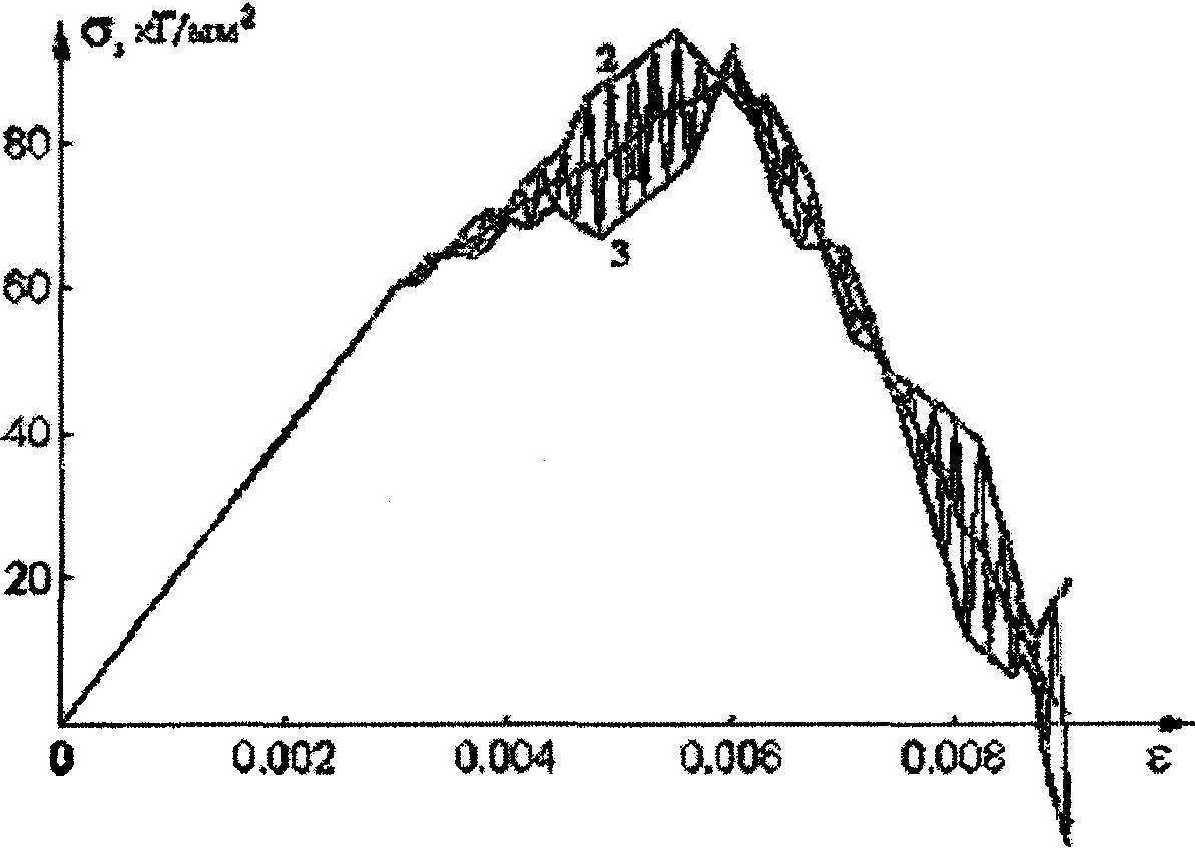
Рис. 3. Пилообразная ломаная при пересчете приближенной зависимости М^ (к*)

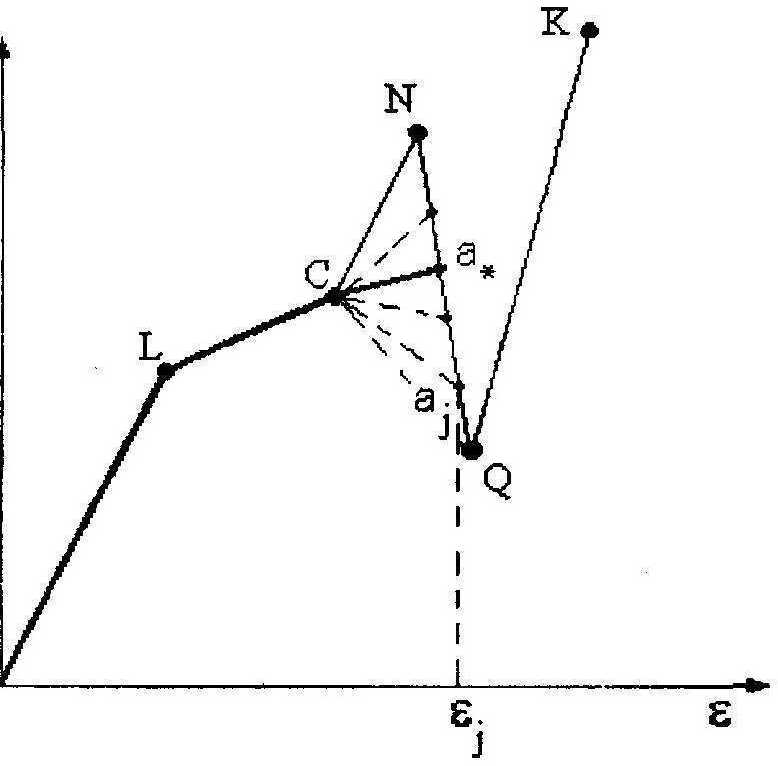
Рис. 4. Схема алгоритма подбора

Построение приближенного решения можно осуществить, применяя следующий алгоритм подбора. Пусть до точки С приближенная диаграмма ст(^) известна, и из этой точки выходит ломаная CNQK (рис.4). Разбиваем отрезок NQ точками Qj и решаем прямую задачу для диаграмм OLCa^ (у -достаточно большое число). Из полученного множества М^^ выделяем элемент М*, удовлетворяющий при к: = Kj неравенству |а^Х^Э ^-^a(^v )| < 3. Этот элемент определяет точку а4 такую, при которой прямой расчет с использованием диаграммы OLCa* дает кривую, достаточно близко расположенную к кривой М^к) (кривая 1, см. рис.2).. Далее процесс повторяем с изменением, при котором вместо точки С берется уже точка а*. В результате проведенных вычислений получаем диаграмму, изображенную на рис.З (кривая 1), которая практически не отличается от диаграммы <7т(е). В заключение отметим, что кривая 1 на рис.З расположена практически посередине между кривыми 2 и 3.