Обратное кроссполяризационное отражение в однородных граничащих средах

Евтифеев А. А., Ломухин Ю. Л. Обратное кроссполяризационное отражение в однородных граничащих средах // Вестник Бурятского государственного университета. Химия. Физика. 2019. Вып. 1. С. 17–23.

Кроссполяризационное обратное отражение — это отражение радиоволн с поляризацией отличной от поляризации падающего на границу раздела излучения.

Известно кроссполяризационное обратное рассеяние при облучении случайно-неоднородных сред, представляющих собой коллоидные суспензии — растворы, содержащие частицы [1]. Механизм деполяризации отраженных волн естественно связывают с многократным рассеянием на частицах. В работе пока-жано, что кроссполяризационное обратное отражение существует в однородных средах, которые допускают теоретическое описание с использованием комплексных диэлектрических проницаемостей. Это сплошные твердые, жидкие, газообразные среды, в которых выполняется условие X >  a , где X — длина волны падающего на границу раздела излучения, a — среднее межатомное расстояние.

Некогеретное обратное отражение при нормальном падении волн на границу раздела. Пусть на границу «воздух — полубесконечная поглощающая среда» падает нормально к границе плоская гармоническая волна, рис. 1.

E = E _o exp[- z ( k_xr + tot )] , (1)

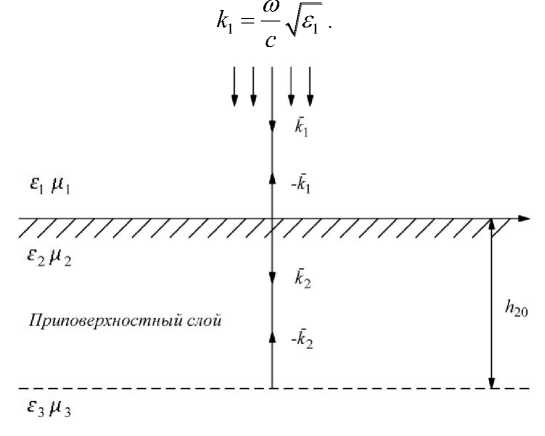
Рис. 1. Схема падения волн на границу раздела

Среды характеризуются параметрами гj = г , - ie ,, E j <<  г ,, г₂ = г ₂ - ie ₂, e₃ = e₃ - ze₃ , д = д = д = 1 . j , j , j зависят только от частоты.

Прошедшая через границу раздела волна, своим полем вызывает поляризацию во второй среде — возбуждает вторичные источники. В результате взаимодействия полей вторичных источников и прошедшей волны формируются преломленная и встречная волны [2]. При этом интенсивность встречной волны пропорциональна интенсивности преломленной волны. Во второй среде, наряду, с когерентной преломленной волной и когерентной встречной волной возбуждается флуктуационные колебания со случайными направлениями поляризации [3]. В результате преломления на границе раздела встречных волн, в первой среде распространяются как когерентные, так и некогерентные обратные волны в направлении строго противоположном падающему излучению.

Уточним механизм обратного когерентного и некогерентного отражения. Как известно, в любой среде при абсолютной температуре отличной от нуля существует собственные тепловые излучения со случайным направлением поляризации. Поскольку интенсивность преломленной волны уменьшается при распространении вглубь среды, то при некоторой глубине h , рис. 1, интенсивность преломленной волны сравнивается со средней интенсивностью теплового излучения. Следовательно, вблизи границы h когерентная преломленная волна трансформируется в некогерентное излучение. Таким образом, до глубины h существует когерентная преломленная волна, после перехода в более глубокую область её поляризация становится случайной. Следовательно, на глубине h образуется граница, при переходе которой интенсивность преломленной волны уменьшается в Р раз, где Р — закон распределения поляризации волн теплового излучения. Такая же трансформация вблизи границы h происходит с кросспо-ляризационной компонентой флуктуационного поля.

Из сказанного следует, что при облучении границы раздела сред имеет место два эффекта: во-первых, возбуждается кроссполяризационное обратное отражение, во-вторых, образуется приповерхностный слой толщиной h . В данном слое формируется как когерентное, так и кроссполяризационное обратное отражение.

Определим глубину приповерхностного слоя, для этого напишем равенство

I (1 - V 1P ( A ,0)^exp[ - 2Im( k ₂ ) h ₂₀ = n ^ - V p ( A ,0) ²|            (2)

где   V PS ( A ,0) = V PS (0)exp( - 2( k. A )²) , V PS (0)       коэффициент Френеля,

— exp(-2(kA)2) — фактор Релея [4], A — средне квадратичное отклонение неровностей границ раздела, k2 = — Лё,, n2 « ё.

c

В (2) с левой стороны представлено выражение для ослабления интенсивности преломленной волны прошедшей от границы раздела до глубины h . Справа — интенсивность теплового излучения в среде. Из (2) определяем h :

1        7 PS     1      11 h 20 = h 20 = ~ T  /, a ln 2 Im( k 2)	1 + V P 2 S (0)	, Im( k 2) >  0 .	(3)
	1 - V 1PS (0)

Значение h^PS есть не что иное, как глубина проникновения когерентной волны при облучении границы поглощающей среды. В случае проводящей среды (3) совпадают с известным значением скин — слоя [5].

Учитывая, что интенсивность кроссполяризационной обратной волны пропорциональна интенсивности преломленной и то, что обратное отражение формируется в приповерхностном слое глубиной h ^PS , используя флуктуационно-диссипационную теорему [6], запишем среднюю интенсивность обратного крос-споляризационного отражения

• < ( EE •) >_±= А п_в— , T ) W^P , ( A ,0) W^P 2 ( A ,0) " W ■ 2 <  A Hf W _{| ?}( \.0, - , (4)

π

где — 0(—, T) — функция Планка, индексы p и s означают соответственно поля ризацию магнитного вектора и поляризацию электрического вектора, Т — абсолютная температура.

_wps _{0) =} V P ( A ,0) + V PS ( A ,0)exp( - 2 ik 2 h 20 )

—

• ^{1,2 1} ’     1 + V PS ( A ,0) V P ^S ( A ,0)exp( - 2 ik₂h ₂₀)

коэффициент отражения от слоя [7].

В (4) VP (А, 0) — коэффициент отражения на границе hP. В силу закона со- хранения энергии должно выполняется условие:

• <    ( EE >_± |(1 - V PS ( А ,0))| = P ² <  ( EE >_±              (6)

Физический смысл равенства (5) состоит в том, что волна с определенной поляризацией пройдя через границу h ^PS трансформируется в излучение со случайной поляризацией, направление которой распределено в интервале 0 ^ 4 п с ве ^{роятностью Р .} При этом интенсивность волны с первоначальной поляризацией уменьшается в Р раз. Другими словами в данном случае проявляется эффект перехода энергии во флуктуации. Из (4) следует, что V 2,3 ^{( А} ,⁰⁾ ~ ^{1 — P} .

Согласно флуктуационно-диссипационной теореме [6], средняя интенсивность теплового излучения может быть представлена как

• <    (EE*) >тепл = f^,T)n12(1 - WP(А,0)2).(7)

В результате трансформации на границе h ^PS средняя интенсивность (4) сравнивается с величиной <  ( EE *) >_теш P . Отсюда определим множитель A .

А=        п2(1 — WP (А,0)2) P

Wp(a,0)wp(a,0)* W1S2(A,0)W1S2(A,0)*,.

Тогда средняя интенсивность кроссполяризационного обратного отражения может быть представлена в виде

• <    (EE*) >±= Pn2(1-W1P(А,0)2) .(8)

Если допустить равномерное распределение направлений поляризации в ин тервале 0 ^ 4п, то P = — . В представленной методике расчета кроссполяриза-4п ционного обратного отражения необоснованным является выбор закона распределения P . Для его уточнения можно использовать результаты экспериментальных исследований.

Экспериментальные исследования

Измерения средней интенсивности кроссполяризационного обратного отражения проводились на созданном измерительном комплексе, рис. 2.

Комплекс состоит из двух параболических антенн, у которых имеется устройства для изменения направления поляризации при излучении и приеме электромагнитных волн.

Антенны располагались на общей несущей. Расстояние между центрами антенн выбиралось с учетом достаточной электромагнитной развязки.

Одна антенна подсоединялась к генератору непрерывного излучения частотой 10 ГГц, другая — к измерительному приемнику ПК7-8.

Рис. 2. Измерительный комплекс

Методика измерений сводилась к следующему: вначале антенны ориентировались строго в зенит при VV и VH поляризациях, в обоих случаях измерялся уровень связи между антеннами, который составлял — . Затем антенны ориентировались строго на поверхность асфальтового покрытия, и при VV и VH измерялся уровень обратного отражения. Поверхность асфальтового покрытия шероховатая.

Результаты нескольких измерений приведены в таблице.

Таблица

№ изм.	Уровень отражения при VV-поляризации, дБ	Уровень отражения при VH-поляризации, дБ	Разница между VV и VH, дБ.
1	36	28	8
2	40	26	14
3	39	30	9
4	36	28	8
5	36	30	6
6	32	27	5
7	34	19	15
8	35	19	16
9	35	21	14
10	38	18	20
11	36	18	18
Сред. Зн.	36	24	12

Из нее следует, что средняя величина разности уровней при VV и VH поляризациях отраженного поля составляет 12 дБ , то есть кроссполяризационное отражение на 12 ∂ Б слабее отражения при кополяризации. Следует отметить, что измерения проведены со значительной погрешностью из-за несовершенства измерительного комплекса, из-за влияния отражений от окружающих объектов и т.д. Поэтому результаты следует считать предварительными. Сравним измеренные и теоретические данные. Для этого воспользуемся формулой (8). В нашем случае ( к_х А )² >>  1 , поэтому в (8) можно заменить W P (А,0) на V P (А,0) . Диэлектрическая проницаемость асфальта на частоте 10 ГГц ^ = 4,3 — z 0,1 , тогда

|VP (A,0)| = 0,4. Подставляя в (8) и, выражая средний уровень кроссполяриза- ционного отражения в дБ, получим    (A, 0) = 10 log —— (1 — 0,4) = —13,21 дБ.

4п

Уровень     обратного     отражения     при     VV     поляризации

^ _v ( A , 0) = 10 log 0,4 = — 3,97 дБ .

Разница a_{v r}( A ,0) и ^ ,, ( A , 0) составляет 9,24 д Б. С учетом погрешностей, результаты измерений и расчётов качественно согласуются между собой.

Заключение

Предложен физический механизм возбуждения кроссполяризационного обратного отражения включающий возбуждения флуктуационных встречных полей и отражение от границы, где средняя интенсивность преломленного поля и средняя интенсивность теплового излучения становится равными. Установлен эффект образования приповерхностного слоя, в котором формируется как когерентное, так и некогерентное обратное отражение.