Обратный поток энергии для оптического вихря с произвольным целым топологическим зарядом

Начиная с работы [1], стало известно об обратном потоке энергии при распространении светового поля в свободном пространстве. В местах обратного потока продольная компонента вектора Пойнтинга принимает отрицательные значения. Этому явлению в оптике посвящено относительно немного работ [1–10]. В [1] показано, что при фокусировке плоской волны с линейной поляризацией с помощью апланатической системы в плоскости фокуса в области первого тёмного кольца интенсивности имеется область, в которой поток световой энергии направлен в обратную сторону по отношению к направлению распространения падающей плоской волны. В [2] теоретически было показано наличие отрицательного значения продольной составляющей вектора Пойнтинга на оптической оси у линейной комбинации двух пучков Бесселя m-го порядка с ТЕ- и ТМ-поляризациями. В [3] рассмотрена практически реализуемая ситуация (фокусировка с помощью апланатической системы) и теоретически и численно показано, что при фокусировке моды Лагерра – Гаусса порядка (0, m)=(0,2) и левой круговой поляризации (σ =–1) на оптической оси в фокусе у продольной проекции вектора Пойнтинга имеются отрицательные значения. В [4] рассмотрена суперпозиция двух произвольных световых полей, у которых разные проекции волнового вектора на продольную ось. Показано, что у таких световых полей имеют место локальные области, в которых продольная компонента силы, действующей на микрочастицу, направлена против волнового вектора светового пучка. В [5] численно показано наличие обратного потока на оптической оси в фокусе вихревой металинзы. В [6] численно показано наличие обратного распространения энергии в векторном пучке Бесселя с дробным топологическим зарядом. Такой световой пучок фактически является линейной комби- нацией счётного числа обычных мод Бесселя. В [7] теоретически получены выражения для плотности вектора Пойнтинга для векторных Х-пучков и необходимые условия для появления обратного потока энергии. В [8] численно показано наличие обратного течения энергии в непараксиальном ускоряющемся 2D-пучке Эйри. В [9] теоретически с помощью локального волнового вектора рассматриваются условия, которые нужно наложить на световое поле, чтобы оно локально имело обратное распространение (или имел место обратный поток энергии). В [10] численно показано, что в вихревом поле с круговой поляризацией, сформированном спиральной зонной пластинкой, вблизи оптической оси имеет место обратный поток световой энергии. Кроме того, известны теоретические работы по изучению свойств вектора Пойнтинга и вектора орбитального углового момента в произвольных и вихревых скалярных и векторных световых полях [11–14]. В [11] исследуются параксиальные вихревые пучки с несколькими фазовыми сингулярностями в поперечном сечении пучка. В [12] найдены спиральные траектории потока энергии для пучков Бесселя и Лагерра – Гаусса, а в [13] исследуется «оптический ток» (optical current) в вихревых пучках.

В данной работе получены общие формулы для проекций электрического и магнитного полей произвольного оптического вихря с целым топологическим зарядом и круговой поляризацией вблизи фокуса апланатической системы, а также выражения для интенсивности и проекций вектора Пойнтинга в плоскости фокуса. Теоретически показано, что при любом m >2 вблизи оптической оси в плоскости фокуса оптического вихря с левой круговой поляризацией имеет место обратный поток энергии, который возрастает по модулю как степень радиальной переменной и вращается вокруг оптической оси по спирали при распространении.

Распределение интенсивности в плоскости фокуса оптического вихря

Рассмотрим с помощью формул Ричардса – Вольфа [1] интенсивность и поток энергии (проекции вектора Пойнтинга) в плоскости острого фокуса произвольного оптического вихря с круговой поляризацией, сфокусированного апланатической системой. Выражения для трёх проекций вектора напряжённости электрического поля оптического вихря в области фокуса были получены в [14]. Ниже мы приведём также три проекции вектора напряжённости магнитного поля, выражение для интенсивности и для трёх проекций вектора Пойнтинга. Для напряжённости электрического поля с круговой поляризацией E = E x e x + i o E y e y , где e x , e y - единичные вектора вдоль декартовых координат, будем считать, что при о =1 - правая поляризация, а при о =-1 - левая поляризация, следуя [14]. Для оптического вихря с топологическим зарядом m и произвольной функцией аподизации зрачка (действительная функция A m ( 9 ))

^Am ^{( 9 ,} Ф ) = ^Am ^{( 9 )}exP ( im ф ) ,                        ⁽¹⁾

где ( 9 , ф ) - углы, задающие точку на сходящемся сферическом волновом фронте, запишем проекции электрического вектора E вблизи фокуса в апланатиче-ской системе в цилиндрических координатах ( r , ф , z ), следуя [14]:

^Ex ( r , Ф , z ) =

= - i m ^{+ 1} e m ^ф ( 1 0, m + Y + 1 2, m + 2 e + Y - 1 2, m - 2 e ^ ) ,

^Ey ( r , Ф , z ) =                                           ⁽²⁾

= i^me m ^ф ( о 1 0, m -Y + 1 2, m + 2 e 2 ^{, ф} + Y - 1 2, m - 2 e ),

Ez (r, ф, z) = -2imemф (y+ IUm+ie^ -Y-11m-1 e   ', где

10,m = B J sin 9 cos1/2 9Am (9) eikcos 9 x x (1 + cos 9) Jm (x )d9,

a

1 1, m ± 1 = B J sin² 9 cos¹ / ² 9 A m ( 9 ) e kcos ⁹ J m ± 1 ( x )d 9 ,     (3)

1m±2 = B J sin 9 cos1/2 9Am (9) eikcos 9 x x (1 - cos 9) Jm±2 (x)d9, где B = kf/2, a = arcsin (NA), x = krsin 9, y+ = (1 ± о) / 2, Jν(x) – функция Бесселя, k – волновое число света, f – фокусное расстояние апланатической системы с числовой апертурой NA.

На основе (2) можно записать выражение для интенсивности в плоскости фокуса ( z = 0) произвольного оптического вихря (1):

I m ( ^r , Ф , ^z = ⁰ ) =

= 2 [ 1 £ m + Y + ( 1 2 ² m + 2 + 2 1 2mm + 1 ) + Y - ( 1 m - 2 + 2 1 12 m - 1 ) ] •

Из (4) видно, что распределение интенсивности в плоскости фокуса имеет осевую симметрию, так как не зависит от азимутального угла ф. И так как у интегралов Ip,q, входящих в (3) и (4), второй индекс показывает порядок функции Бесселя, то из (4) можно заключить, что на оптической оси (r = 0) интенсивность будет равна нулю при любом m > 2. При m = 1,2 на оптической оси интенсивность оптического вихря с левой круговой поляризацией (о = -1) будет отлична от нуля. Но в обоих случаях (m = 1,2) световой поток не будет распространяться вдоль положительного направления оптической оси: при m = 1 поток энергии на оси будет нулевой, а при m = 2 – обратный.

Продольная проекция вектора Пойнтинга в фокусе оптического вихря

Чтобы доказать наличие обратного потока в фокусе оптического вихря с произвольным целым топологическим зарядом m ≠ 0, приведём выражения для трёх проекций вектора напряжённости магнитного поля: н ( r , ф , z ) = - i^m о 1 0, m e" ^ф + 2 i^{m + 1} Y + sin ф I, , m e i ^{m + 1) ф} +

+ 2 i^{m + 1} Y - sin ф 1 ₁ , _me^{i ( m - 1) ф} +

"/ e i ^{( m + 2) ф} I I

⁺ i 1 + e I 2 m m + 2

^my p i ^{( m -2}M ]

i 1 - e I 2 m m - 2

-

2( m + 1)

kr

1 1, m + 1

-

-

2( m - 1)

kr

I

,

H y ( r , ф , z ) = - i^{m + 1} 1 0, m e m ^ф - 2 i^{m + 1} Y + cos ф 1 1, m e i ^{m + 1) ф} -

- 2 i^{m + 1}

Y - cos ф 1 _{1 m} e ^{( m 1) ф}

-

-im+1v pi(m+2M T i     1+ e          I I 2, m+2

- i m ^{+ 1}

-

2( m + 1)

-

kr

¹ 1, m + 1

2( m - 1) kr

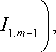
Y e i ⁽ m ^{- 2)} ф

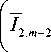
H z ( r , ф , z ) = i m ^{+ 1} Y + e im ^{+ 1) ф}| 1 2, m + 1 + T- 1 0, m I kr

-

m+113,m-1 eim ф (о cos ф + i sin ф) + im+1Y-12, m-1 ei( m-1)ф, где

I ,, _m = B J sin 9 cos ³/² 9 A m (9) e ik ^{cos 9} x (1 + cos 9) J_m ( x ) d9,

13,m-1 = B J sin2 9 cos1/2 9Am (9) ekcos9 x x (1 + cos 9) Jm _1 (x )d9,

a

I 1, m = B J sin ³ 9 cos ¹/² 9 a- (9) x e k ^{cos 9} J m ( x ) d9,

I,m±2 = B J sin 9 cos3/2 9Am (9) eikcos9x x (1 - cos 9) Jm ±2( x )d9,

12,m±1 = B J sin2 9 cos1/2 9Am (9) eikcos9x x (1 - cos 9) Jm±1(x)d9.

С помощью (2), (3), (5) и (6) найдём продольную проекцию вектора Пойнтинга [1] S = c Re [ E x H ]/(8 n)

Sz =   ReEexH* -EH*), z 8„ V x y y x)

Далее приведём выражение, аналогичное (11) и (13), для оптического вихря с левой круговой поляризаци-

с точностью до константы c1 8 п , где c - скорость света в вакууме, Re(...) - действительная часть числа, в плоскости фокуса ( z = 0):

S mz = 2 1 о, m ( I ,. m + Ц , m ) +

ей и произвольным целым топологическим зарядом. Вблизи оптической оси ( kr << 1) в плоскости фокуса для продольной проекции вектора Пойнтинга имеет место приближённое выражение:

^{+ 2} У + I 2, m + 2 I ¹ 2, m + 2 ^{+ 1} 1, m

2( m + 1) I Y + kr ^{1 m + 1} J

Smz-(r ^ 0>

2 B ²( kr )²⁽ ■ ^{- 2)}

2 2( m -

2) [(m - 2)!]2

X

^{+ 2} У - I 2, m - 2 I ¹ 2, m - 2 ^{+ 1} 1, m

2( m — 1) _T Y

I «И-1

(aa                                                                                 i

x I J sin ^{m 1} 9 cos^1/2 9 A m ( 9 )(1 - cos 9 )d 9 I <  0.

Из (8) видно, что продольный поток энергии имеет круговую симметрию. Наличие в (8) слагаемых с отрицательными знаками показывает, что в плоскости фокуса можно найти локальные области, в которых продольная проекция вектора Пойнтинга будет отрицательной. Интересно выяснить, может ли эта локальная область располагаться вблизи оптической оси.

Из (14) видно, что при любом целом m > 2 на оптической обратный оси поток равен нулю, а вблизи оси с ростом радиальной переменной обратный поток растёт по модулю как степень 2( m - 2) радиальной переменной.

Обратный поток энергии вблизи оптической оси в плоскости фокуса

Из (8) следует, что при m = 1 продольный поток энергии оптического вихря с левой круговой поляризацией

S 1 z

-

= ² [ I 0,1 ⁽ I 0,1

⁺ 1 1,1

^{) + 1} 2,1 ^{( 1} 2,1

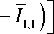
Поперечные составляющие вектора Пойнтинга в плоскости фокуса

Можно показать, что поперечный поток энергии (как прямой, так и обратный) у оптического вихря с левой круговой поляризацией вблизи плоскости фокуса вращается. Для этого найдём поперечные составляющие вектора Пойнтинга:

S x - = ^- Q m ⁽ r ^)sin Ф , S y - = Q m ⁽ r ^)cos Ф ,         ⁽¹⁵⁾

где

^Qm ⁽ r ) = ( ¹ 0, m ^{+ 1} 2, m - 2 ) ( ¹ 2, m - 1 ^{+ 1} 3, m - 1 ) ⁺

на оптической оси ( r = 0) равен нулю, а при m = 2 продольный поток для левой круговой поляризации

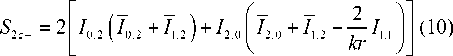
на оптической оси обратный:

S 2 z - ( r = 0, z = 0) =

2 ( a 1/2                      Y (11)

= - 2 B ² 1 J sin 9 cos^1/2 9 A 2 ( 9 )(1 - cos 9 )d 9 I <  0.

То есть вблизи оптической оси поток энергии (10) распространяется в обратном направлении по отношению к падающему потоку энергии. При m = 3 вместо (10) получим:

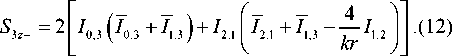
Из (12) следует, что вблизи оптической оси ( kr << 1) в плоскости фокуса имеет место обратный поток энергии, который на самой оси равен нулю и возрастает по модулю квадратично с ростом радиальной переменной r :

S3 z -(r ^ 0)«

-

B ²( kr )²

X