Обратный поток энергии у непараксиального оптического вихря в ближней зоне

В оптике активно изучаются оптические «тракторные» пучки ( optical tractor beams ) [1 –4]. Это пучки, которые позволяют «притягивать» микрообъекты (например, клетки бактерий [1]) к источнику света. Например, в [4] «тракторный» пучок формируется с помощью металинзы-аксикона в плёнке кремния. Параллельно исследуется другой интересный эффект в оптике – обратное распространение ( reverse propagation ) [5] или обратный поток энергии ( negative energy flux [6] или energy backflow [7]). Этот эффект возникает, когда продольная составляющая вектора Пойн-тинга направлена в обратную сторону по отношению к направлению распространения пучка света. Известен также эффект углового трактора [8], когда в вихревом пучке на разных радиусах от оптической оси поток энергии вращается в разные стороны.

Обратный поток энергии описан в разных статьях, в которых не занимались им напрямую, а он получался как «побочный эффект». В [9] численно показано наличие обратного потока при прохождении через нанополоску золота на поверхности InP, хотя сами авторы на это не обратили внимания, а констатировали только, что свет не проходит в среду InP при нормальном падении в присутствии золотой нанополоски. В [10] численно было показано наличие обратного потока при фокусировке света в градиентной микролинзе на выходной торец. Обратный поток объяснялся наличием бегущей по торцу микролинзы поверхностной волны, которая то входит, то выходит из среды. В [11] получено уравнение (19) для продольной компоненты вектора Пойнтинга в фокусе пучка Бесселя нулевого порядка с линейной поляризацией, из которого следует, что поток энергии на некоторых радиусах от оптической оси меняет знак (распространяется в обратном направлении). Правда, в [11] этого не заметили. Ранее, в [12] была получена аналогичная формула (15) для продольной составляющей вектора Пойнтинга пучка Бесселя нулевого порядка. В [12] заметили, что на определённых радиусах поток энергии может быть направлен в обратном направлении по отношению к направлению распространения пучка. В [13] численно показано возникновение обратного потока энергии при прохождении через субволновое отверстие. Обратный поток возникал вокруг сингулярностей, которые появлялись вблизи отверстия. Ранее, ещё в 1950 году, был теоретически обнаружен обратный поток энергии вокруг изолированных нулей интенсивности при решении задачи дифракции плоской волны на металлической полуплоскости [14].

Обратный поток энергии целенаправленно искали в разных векторных пучках света с разным состоянием поляризации. В [15] теоретически показали наличие обратного распространения энергии в линейной суперпозиции ТЕ- и ТМ-поляризованных пучков Бесселя произвольного порядка. В [6] обнаружили отрицательный поток энергии в Х-волнах. Х-волны – это полностью векторные пучки, полученные с помощью потенциала Герца из скалярного точного решения скалярного волнового уравнения, и их амплитуда пропорциональна гипергеометрической функции Гаусса 2F1(a, b, c; x). В [16] численно показано, что обратный поток энергии имеет место в векторных пучках Бесселя с дробным топологическим зарядом. В этом случае амплитуда всех составляющих векторов электрического и магнитного полей выражается через бесконечные суммы функций Бесселя. В [17] эффект негативного распространения пучка найден в непараксиальных пучках Эйри.

Обратный поток энергии был обнаружен (правда, только теоретически) при острой фокусировке лазерных пучков. Это особенно интересно, так как в области фокуса обратный поток оказывается сравнимым по величине с прямым потоком энергии. В [18] получено простое выражение для продольной компоненты вектора Пойнтинга в фокусе апланатической системы при фокусировке плоской волны с линейной поляризацией (уравнение (3.21)), из которого следует, что на некоторых радиусах (вблизи тёмных колец) имеет место обратный поток энергии. Этот эффект в фокусе идеальной линзы ранее был замечен в [19]. В [20] численно показано, что при фокусировке параксиального Гауссова пучка с помощью сферической линзы, ограниченной апертурой, в плоскости фокуса и рядом с ней на некоторых радиусах возникают тёмные кольца Эйри, в которых имеет место фазовая сингулярность.

Позже Берри с помощью асимптотик показал, что такие сингулярности возникают в фокусе непараксиального Гауссова пучка и без ограничения линзы апертурой [21]. В [21] также показано, что вокруг сингулярности фазы возникает круговой поток энергии, в том числе и обратный поток. В [22] Воляр численно показал, что в фокусе линейно поляризованных векторных непараксиальных пучков Гаусса (сферические моды низших порядков) сечение пучка эллиптическое, и вокруг центрального пятна имеются «острова сингулярности» (вместо колец Эйри), рядом с которыми возникает обратный поток энергии. В [23] аналогичные «острова сингулярности» и обратный поток рядом с ними численно обнаружен в плоскости фокуса векторных непараксиальных Гауссовых вихревых пучков с круговой поляризацией. В [24] численно было показано, что с помощью одной спиральной металинзы с высокой числовой апертурой можно менять место и величину обратного потока в плоскости фокуса с помощью изменения состояния поляризации падающего излучения (ТЕ- или ТМ-поляриза-ция, левая или правая круговые поляризации). В этих работах [18 – 23] обратный поток энергии был обнаружен в периферийных кольцах картины дифракции в фокальной плоскости. И только в [25] численно показано, что при непараксиальной фокусировке пучка Лагерра – Гаусса с топологическим зарядом 2 и обратной (левой) круговой поляризацией в плоскости фокуса на оптической оси (в центре фокусного пятна) имеет место обратный поток энергии.

Из приведённого краткого обзора работ по обратному потоку следует, что этот эффект имеет универсальную природу: он возникает в фокусе плоской волны [18, 19], в фокусе ограниченного параксиального [20] и неограниченного непараксиального [21] скалярных Гауссовых пучков, а также в фокусе непараксиальных пучков Лагерра – Гаусса [24]. Он возникает также в фокусе непараксиальных векторных пучков с линейной [23] и круговой поляризациями, в различных векторных модовых пучках (Бесселя [15, 16], Эйри [17], Х-волны [6]), при фокусировке на границу раздела сред [10], вблизи наноструктурированных поверхностей [9, 13]. Заметим, что у параксиальных световых полей (при отсутствии ограничивающей диафрагмы) продольная компонента вектора Пойнтинга, пропорциональна интенсивности и не меняет знака [8]. То есть у параксиальных полей не может быть обратного потока энергии в свободном пространстве.

Рассматриваемый эффект обратного потока энергии может быть использован для демонстрации эффекта «оптического трактора» [26, 27], когда микрочастица, захваченная в специальным образом сформированный лазерный пучок, двигается против направления распространения света в пучке.

В данной работе, в отличие от работы [18], в которой используется формализм Ричардса – Вольфа, работ [6, 15, 16, 17, 22, 23], в которых используются известные точные решения уравнений Максвелла (X-волны, пучки Бесселя, Эйри, квази-Гаусса [5], векторные непараксиальные гауссовы пучки), получены общие выражения для проекций вектора Пойнтинга для любого вихревого электромагнитного поля с эллиптической поляризацией методом разложения по плоским волнам. Получено условие, при котором в начальной плоскости пучка (в перетяжке) возникает обратный поток энергии. Из этого условия следует, что только при наличии неоднородных затухающих волн с большими поперечными проекциями волнового вектора в перетяжке может возникнуть обратный поток энергии. Причём чем больше вклад затухающих волн в общую амплитуду пучка, тем больше величина обратного потока энергии, который при этом сравним по величине с прямым потоком.

• 1.    Интенсивность и продольная проекция вектора Пойнтинга

Общее решение уравнения Гельмгольца

( V 2 + к ² ) P ( x , y , z ) = 0,                             (1)

где V ² = d ²/ d x ² + 5 2 / 5 y ² + 5 2 / 5 z ², можно записать в виде разложения по спектру плоских волн [28] да да

P ( x , У , z ) = ( 2 п к ) ^-1 J J A ( ^ , n ) х

-да -да

х exp ^ik (x с + yn + z 41 — ^2 —П2

] d ^ d n ,

где A (ξ, η) – амплитуда спектра плоских волн, k – волновое число света. Для оптического вихря с топологическим зарядом n амплитуду спектра плоских волн можно записать в полярных координатах (ρ, θ) в виде

A(^,n) = A(р, 6) = An (р)ein8.                       (3)

С учётом (3), скалярную функцию (2) в цилиндрических координатах ( r, φ) запишем в виде:

P ( r , ф , z ) = i n k ^{- 1} e^{in ф} 1 1, n ,                                   (4)

где да

1 1, n = j A n ( р ) e k J n ( kr р ) Р d p ,                 (5)

а J n ( x ) - функция Бесселя первого рода n -го порядка. С помощью решения уравнения Гельмгольца (1) можно рассчитать все проекции векторов напряжённости электрического и магнитного поля, в совокупности удовлетворяющих уравнениям Максвелла. Для этого воспользуемся методикой, например, описанной в [29]. Будем формировать световое поле с эллиптической поляризацией, тогда поперечные проекции вектора напряжённости электрического поля можно записать в виде

• 3    ⁵ P _ / х . д P E x ( x , У , z ) = —, E y ( x , У , z ) = ia — , д z                  д z

  
  

где a =±1 - спиновый индекс, определяющий левую и правую круговую поляризацию ( a =+1 для правой поляризации и a =-1 для левой поляризации). При других значениях a выражение (6) описывает поле с эллиптической поляризацией. Подставляя (4) в (6), получим для поперечных проекций электрического поля:

E x ( r , ф , z ) = i n ^{+ 1} e^{in ф} 1₃ , _n

E y ( r , ф , z ) = - i n a e^{in ф} 1 3

где да

1 3, n = j V 1 -p ² A n ( p ) e ik J n ( kr p ) p d p .          (8)

Продольную проекцию найдём с помощью соотношения [29]:

д P

E ⁽ x ^, у ^, z ) = -— д x

дP i a— ду

и получим

E z ( r , ф , z ) = i n [у + e^{i ( n + 1 )ф} 1 2, n +1 -Y - e^{i ( n - 1 )ф} 1 2, n -1 ] , (10)

где да

12n = j An (p) eikzJn (krp)p2dp, а y± = (1± a)/2. Из (7) и (10) можно записать уравнение для распределения интенсивности на любой плоскости, перпендикулярной оптической оси z > 0, для произвольного оптического вихря (3) c эллиптической поляризацией:

I = |Y + Г 1 2, n 4 +|Y - Г I 2, n +

+ ( 1 + |a| ² )| I 3, n |² - 2Re { Y - Y + I 2*, n -1 1 2, n +1

Из (11) видно, что для оптического вихря с круговой поляризацией (то есть либо Y - =0, либо Y ₊ = 0) распределение интенсивности осесимметричное, так как не зависит от полярного угла ф . Из (11) следует, что распределения интенсивности для вихревых пучков с левой и правой круговыми поляризациями разные:

I + = 2| I з, n I' + \ 1 2, n +1| ² , I - = 2| I з, n |² +| I 2, n -1| ².

Из второго уравнения (12) для левой круговой поляризации при n = 1 следует, что интенсивность на оптической оси отлична от нуля

да

I - ( r = 0, z ) = | I 2,0, ² = j A ( p ) e^ikz p ²d p >  0, (13)

но так как вклад в интенсивность (13) на оптической оси даёт только продольная компонента электрического поля (10), то свет вдоль оси распространяться не будет, то есть не будет потока энергии вдоль оптической оси. При n >1 на оптической оси интенсивность (11) всегда будет равна нулю. Поперечные составляющие вектора напряжённости магнитного поля можно найти из уравнения Максвелла для монохроматического поля:

H = - -k rot E .(14)

Получим:

H x ( r , ф , z ) = ¹ iⁿ [y + e^{i ( n + 2 )ф} 1 2, n +2 -

2 L

-Y - e^{i ( n - 2 )ф} 1 2, n -2 +a e^{in ф} ( 2 1 1, n - 1 2, n ) ] ,

H_y ( r , ф , z ) = — i^{n + 1} [ y + e^{i ( n + 2 )ф} 1 2, n +2 +

_ 2 L(16)

+ Y-ei(n-2)ф 12,n-2 - einф (211,n -12,n)], где

12,n = j p2 An (p) eikJn (krp)pdp.(17)

С помощью поперечных проекций электрического (7) и магнитного (15), (16) векторов световой волны можно получить выражение для продольной проекции вектора Умова - Пойнтинга (потока энергии), согласно формуле [16] S = c Re[ E х H * ]/(8n):

S z = ( c /8 п ) Re ( E x H * - E y H * ) ,                 (18)

где Re - вещественная часть числа. Подставляя в (18) выражения (7), (15), и (16), получим (с точностью до c /(8n)):

S z = Re { 1 3* n ^[ ( 1 + |a|² ) ( 1 1, n - 1 2, n /2 ) -

L\                        '                 (19)

• - Y - Y₊ e^{2i ф} 1 2. n +2 - y + Y - e ^-2 i ^ф 1 2,n -2 ] } ,

• 2. Обратный поток энергии в начальной плоскости

и для случая круговой поляризации ( a =±1):

S z = Re { 1 3*, n ( 2 1 1, n - 1 2, n ) } .                           (20)

Из (20) следует, что продольный поток энергии радиально-симметричный и одинаковый для левой и правой круговых поляризаций, в отличие от распределения интенсивности.

Пусть для простоты амплитуда плоских волн описывается действительной функцией A n ( р ), тогда, подставляя в (20) из (5), (8) и (17), вместо (20) при z =0 получим:

S z = j V 1 -р ² A n ( р ) J n ( kr р ) Р d p

X

X

да

j ( 2 -р ² ) A n ( р ) J n ( kr р ) р d p 0

Анализ выражения (21) можно проводить только численно, выбирая подходящие функции в качестве амплитуды спектра плоских волн A n ( р ). Чтобы получить конкретный аналитический результат, рассмотрим гипотетическую функцию амплитуды спектра плоских волн в виде линейной комбинации двух дельта-функций Дирака. Физически это означает, что у светового поля часть энергии сосредоточена в узкой области спектра распространяющихся плоских волн, а часть – в области затухающих волн:

A n ( р ) = A 8 ( р-р 1 ) + B § ( р-р 2 ) ,              (22)

где A >0, B > 0, 0< р 1 < 1, 1 <  р ₂< да .

Тогда, вместо (21), получим:

S z = a V 1 - р ? J n ( kr р 1 ) р 1 X

x^[ A ( 2 -р 2 ) J n ( kr р 1 ) р 1 -                          (23)

-B(р2 -2) Jn (krр2 )р2].

Заметим, что пучок Бесселя любого порядка является решением непараксиального уравнения Гельмгольца для любого масштаба ( k р 1 <1 - распространяющиеся пучки Бесселя, k р ₂ > 1 - исчезающие или затухающие пучки Бесселя). Исчезающие пучки Бесселя используют для преодоления дифракционного предела в ближней зоне [30, 31]. Вблизи оптической оси ( kr р 1 < kr р ₂<<1), оставляя в разложении Тейлора функции Бесселя только первый член, вместо (23) получим:

S z » A ТТ-Р ²

( kr ) n р Г ^{+ 1}

----------X n!2n

( kr ) n

X(n!?'Г-[ A(2 - р2) рГ+1 - B(р2 - 2) рГ+1 ] < 0.

Из (24) следует, что S z <0 при выполнении условия

A

— <

B

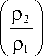
n +1

Г р 2 - 2 ) 1 2 -р 2 ^J

поток энергии вблизи оптической оси в начальной плоскости обратный. Условие (25) возможно, только если р ₂>2^1/2, то есть затухающие волны должны иметь большой коэффициент затухания. Из (24) видно, что при n =0 максимальный обратный поток будет на оптической оси.

3. Поперечные проекции вектора Пойнтинга

Для нахождения поперечных проекций вектора Пойнтинга надо знать продольную составляющую вектора напряжённости магнитного поля (14):

H z ( r , ф , z ) = - Г + ^{+ 1} [y + ei^^{n + 1} ) ^ф 1 4, n +1 + Y - e i ⁿ - ¹ ) ^ф 1 4, n -1 ] ,(26)

где

да

1 4, n = JV 1 -р ² A n ( р ) e k J n ( kr p ) p ²d p .        (27)

Далее найдём поперечные проекции вектора Пойнтинга в начальной плоскости ( z =0) только для оптического вихря с левой круговой поляризацией (для правой находится аналогично) и с точностью до постоянной c /(8π):

S . _ = Re ( E y - H z - - E z - H ;- ) , S y - = Re ( E z - H . - - E . - H z - ) .

Подставляя в (28) выражения для проекций электрического и магнитного векторов для левой круговой поляризации (7), (10), (15), (16) и (26), получим:

S . - = - sin ф Q n ( r ), S y - = cos ф Q n ( r ),

где

Q n ( ^r ) = I 3, n I 4, n -1 ⁺ 2 I 2, n -1 ( I 2, n -2 + ² 1 1, n ^- I 2, n ) .    ⁽3⁰⁾

При получении выражения (30) мы предполагали, что все интегралы – действительные числа, то есть учитывались только распространяющиеся волны. Из (29) и (30) видно, что поток энергии в начальной плоскости ( z =0) направлен по касательной к окружности любого радиуса с центром в начале координат (на оптической оси). То есть вблизи начальной плоскости поток энергии вращается по спирали по часовой или против часовой стрелки в зависимости от знака функции (30).

Для получения конкретного аналитического результата предположим, что амплитуда спектра плоских волн описывается δ-функцией Дирака: A n ( р ) = 5 ( р - р ₀), где 0< р ₀<1. Тогда интегралы, входящие в (30), заменяются на подынтегральные выражения, и вместо (30) получим линейную комбинацию двух функций Бесселя:

Q n ( r ) = J n -1 ( kr р 0 )^[ AJ n ( kr р 0 ) + BJ n -1 ( kr р 0 ) ] ,

A = 2р0 (1 -р0),

D _ n -1 4

^B = -:    ^р 0 .

kr

В (31) . o = kr р ₀. Из (31) видно, что при г > 1 величины A и B положительные. Смена знака функции Q n ( r ) происходит в точках r m , пропорциональных корням функции Бесселя ( г -1)-го порядка: J_n _i ( y _n -i, m ) = 0, m = 1, 2, 3… Причём, так как нули функции Бесселя перемежаются y _n -1,1 < Y n ,1 < Y n -1,2 < Y n ,2 <  ^ , то перед корнем Y _{n -1} , m и вблизи этого корня обе функции Бесселя г -го и ( n – 1)-го порядков будут иметь одинаковые знаки (то

есть функция Q n ( r ) положительная). После корня у n _-1 , m и вблизи него знак функции Бесселя ( n - 1)-го порядка изменится, а знак выражения в круглых скобках в (30) ещё не изменится, и поэтому у всего выражения (31) знак будет отрицательный. Поэтому функция Q n ( r ) будет отрицательная при Г т <  r <  Г т + 5 , где Г т = у n -1, _т /( k p o ), а 5 - некоторая неизвестная величина, определяемая расстоянием между соседними корнями 5 <( у _n , _т - у _n _ ₁ , _т )/( k p ₀). Чтобы определить, на каких радиусах в картине интенсивности происходит смена знака функции (31), запишем интенсивность (12) для левой поляризации с учётом выбранной амплитуды спектра плоских волн A n ( p ) = 5 ( p - p ₀), 0 <  p ₀< 1. Тогда получим:

• I —    = CJ n ( x o ) + DJ - 1 ( x o ),

• 4. Моделирование

C = 2 p 0 (1 -p 0 ),                                   (32)

D = p4.

Из (32) следует, что локальные минимумы (тёмные кольца) будут находиться на радиусах, расположенных между корнями двух соседних функций Бесселя J_{n -1}( x ), J_n ( x ), то есть примерно на радиусах r m * ( Y n -1, т + Y n , т )/(2 k p 0 ), т = 1,2,3... Сравнивая выражения (31) и (32), приходим к заключению, что отрицательные значения функции Q_n ( r )<0 (поток энергии вращается по часовой стрелке) будут лежать на внешних сторонах светлых колец в распределении интенсивности (32) при г_т <  г <  г_т + 5 <  Г т . На внутренних сторонах (а вернее, на остальной части светлого кольца) светлых колец ( Г т <  r <  г_{т + 1}) вращение потока энергии будет против часовой стрелки ( Q_n ( r ) > 0).

Рассмотрим световое поле с угловым спектром (22). Это поле представляет собой суперпозицию двух мод Бесселя - одной распространяющейся и одной затухающей:

E x ( x , У , z ) = e in ^ф [ Ae ikz' ' Jn ( kr p 1 ) +

+iBek v1^ Jn (kr p2)], Ey = i aEx.

Тогда, согласно (25), при условии

A < f p2)n f p2 - 2 ) I1 -p?B Ip1 J 12-p2 J V pi -1

вблизи оптической оси в начальной плоскости возникает обратный поток энергии. Выполнения условия (34) всегда можно добиться увеличением вклада B затухающих волн.

Для численного моделирования выберем следующие параметры: длина волны X = 532 нм, p1=0,8, p2 = 2,4, A = 1, топологический заряд n = 3, поляризация - левая круговая (а = -1) и правая круговая (а = +1), расчётная область z = 0, -R < x, y < R (R = 2,5X). Из (34) следует, что для возникновения обратного потока необходимо, чтобы A /B <20,53. Вы- берем B = 1 и B =10. На рис. 1 приведены распределе -ния интенсивности и потока мощности суперпозиции мод Бесселя (33) в начальной плоскости для разного вклада затухающей моды B =1 (рис. 1 а, б) и B =10 (рис. 1 в, г), а также для разной круговой поляризации.

Из рис. 1 видно, что при усилении вклада затухающих волн усиливается и мощность отрицательного светового потока. Так, при B = 1 максимальная (по модулю) мощность отрицательного потока составила 7,4% от максимальной мощности положительного потока, в то время как при B = 10 это соотношение составило 75 %. Также видно, что отрицательный поток возникает в первом световом кольце, так как кольцо у затухающей моды Бесселя имеет меньший диаметр.

Далее рассмотрим формирование отрицательного потока для безвихревого поля ( n = 0). На рис. 2 приведено распределение интенсивности и потока мощности суперпозиции мод Бесселя (33) в начальной плоскости. Вклад затухающей моды B =10, поляризации - левая круговая, остальные параметры те же, что и на рис. 1.

Из рис. 2 видно, что в этом случае максимальный отрицательный поток формируется в центре дифракционной картины.

В эксперименте найти и зарегистрировать обратный поток энергии достаточно трудно, так как он возникает в области светлых колец в распределении интенсивности (рис. 1). Поэтому для обнаружения обратного потока нужно одновременно измерять и распределение интенсивности в плоскости фокуса, и распределение модуля потока энергии. Если на одном и том же радиусе в плоскости фокуса интенсивность отлична от нуля (светлое кольцо), а распределение модуля вектора Пойнтинга равно нулю (тёмное кольцо), то в этом месте поток энергии распространяется в обратном направлении. Заметим, что при обратном распространении рассмотренного вихря картины интенсивности и потока энергии такие же, как на рис. 1, будут возникать в плоскости фокуса.

Заключение

В работе на основе разложения по плоским волнам получены все шесть проекций векторов напряжённости электрического и магнитного поля для оптического вихря с произвольным целым топологическим зарядом, круговой поляризацией и произвольной радиально-симметричной действительной функцией амплитуды плоских волн. Получены также выражения для распределения интенсивности и всех трёх проекций вектора Пойнтинга в начальной плоскости оптического вихря только с левой круговой поляризацией. В частном случае узкого углового спектра плоских волн (пучок Бесселя) показано, что при наличии в начальном световом поле неоднородных затухающих волн на оптической оси может возникать обратный поток световой энергии. Этот обратный поток можно использовать, чтобы «затянуть» микрочастицу в центр кольцевой перетяжки вихревого пучка, то есть продемонстрировать эффект «оптического трактора». Также показано, что в начальной плоско- сти (в плоскости перетяжки) имеет место эффект «углового трактора», когда на разных радиусах относительно оптической оси поперечный поток энергии вращается по часовой или против часовой стрелки. С помощью полученных общих выражений можно анализировать особенности продольного и поперечного светового потоков энергии и для других известных точных решений уравнения Максвелла.

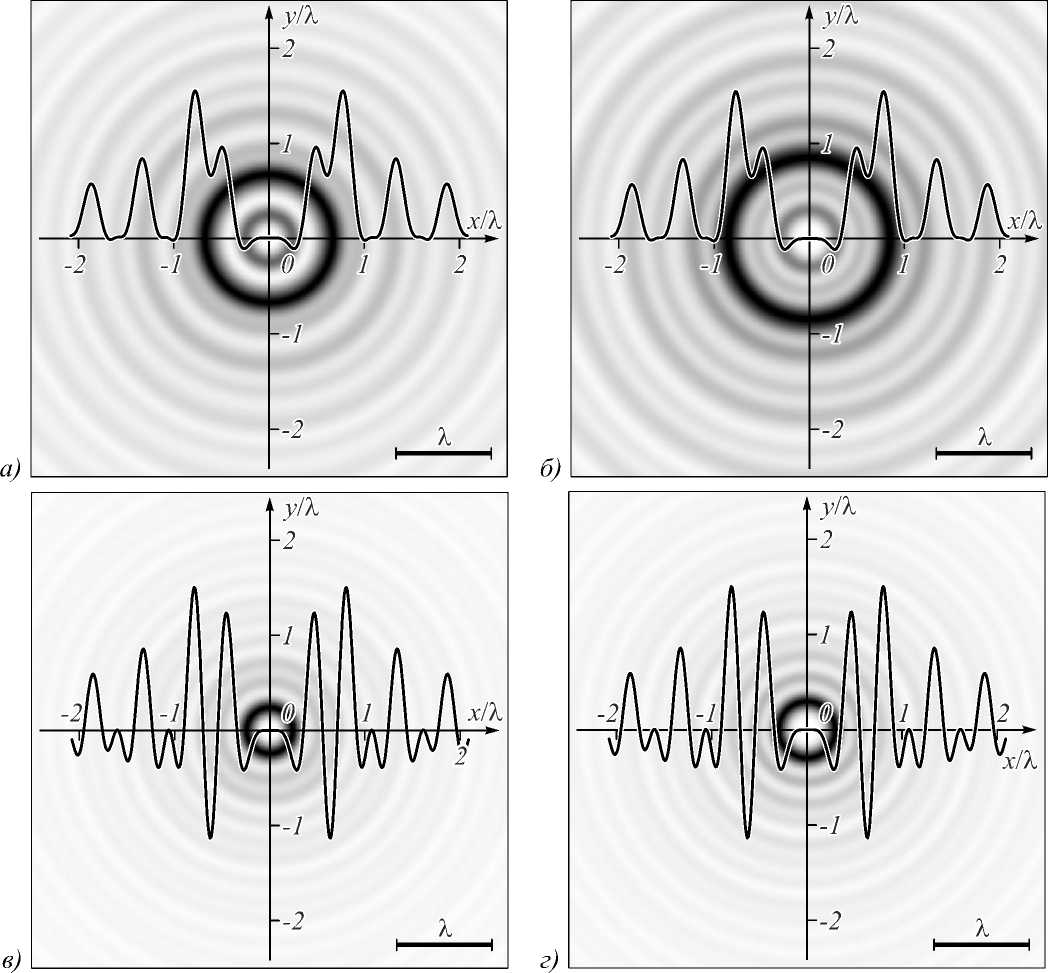
Рис. 1. Двумерные распределения интенсивности (негатив) и наложенные на них одномерные распределения потока мощности суперпозиции двух мод Бесселя (33) в начальной плоскости (z = 0) для разного вклада затухающей моды B = 1 (а, б) и B = 10 (в, г), а также для левой (а, в) и правой круговой поляризации (б, г)

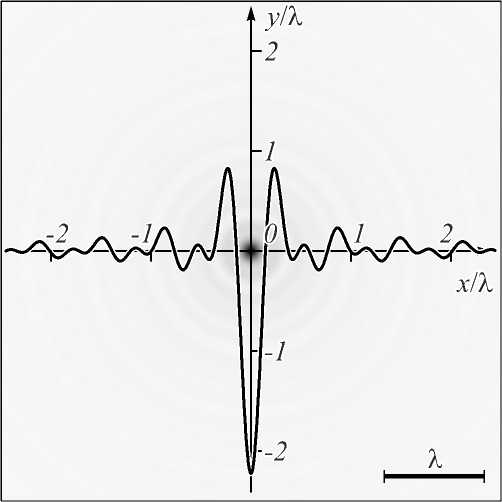
Рис. 2. Двумерное распределение интенсивности (негатив) и наложенное на него одномерное распределение потока мощности суперпозиции двух мод Бесселя (33) в начальной плоскости (z = 0)

Работа выполнена при поддержке Российского научного фонда (грант 17-19-01186) в части «Интенсив- ность и продольная проекция вектора Пойнтинга», Российского фонда фундаментальных исследований (грант 18-29-20003 в части «Обратный поток энергии в начальной плоскости» и грант 18-07-01129 в части «Поперечные проекции вектора Пойнтинга»), а также Министерства науки и высшего образования РФ в рамках Государственного задания ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части «Моделирование».