Обратный поток энергии в фокусе цилиндрического векторного пучка

Цилиндрические векторные пучки [1] известны в оптике достаточно давно, однако интерес к их изучению не ослабевает [2–4].

Поляризация в поперечном сечении таких пучков непрерывно меняет своё направление, совершая полный оборот при изменении азимутального угла от 0 до 2π. При этом ранее уже предпринимались попытки сделать обобщение цилиндрических векторных пучков, рассмотрев такие пучки, в которых направление поляризации совершает несколько оборотов. Такие пучки в литературе получили название цилиндрических векторных пучков высших порядков.

Например, в статье [5] рассматривалась фокусировка радиально-поляризованных пучков высоких порядков вида g l (φ) =cos l φ i + sin l φ j , где l – порядок пучка, i , j – орты в декартовой системе координат, выбранной таким образом, что орт k совпадает с осью симметрии пучка. Распространение мод высших порядков со смещённым центром рассматривалось численно с помощью преобразования Френеля в [6]. В [7] также численно с помощью преобразования Френеля исследовалась дифракция мод высших порядков на отверстии в форме щели.

Экспериментально такие пучки были получены с помощью пространственных модуляторов света [8,9] и элементов, рассчитанных на основе фазы Панха-ратнами–Берри [10].

В перечисленных выше работах изучалось только поведение электрической составляющей светового поля, что не позволяет вычислить значение вектора Пойнтинга в фокусе. В соответствии с [11] сила, действующая на частицу, пропорциональна по абсолютному значению и совпадает по направлению с вектором Пойнтинга. Если некоторый пучок в своём поперечном распределении будет содержать отрицатель-

6179-2018-42-5-744-750.

ную составляющую, то частица, подсвеченная таким пучком, должна двигаться в сторону источника света. Наличие в фокусных пятнах областей с отрицательными значениями продольной проекции вектора Пойнтинга было обнаружено достаточно давно [12]. Однако лишь в прошлом году удалось обнаружить такие фокусные пятна, в которых отрицательные значения сопоставимы по абсолютной величине с положительными значениями. В работе [13] моделировалось прохождение света через металинзу, осуществляющую поворот направления поляризации и фокусировку. Численно с помощью FDTD-метода было показано, что такая линза, освещаемая светом с круговой поляризацией, может формировать фокусное пятно, в котором поток энергии вдоль оси распространения пучка S z имеет отрицательное значение. В работах [14, 15] было сделано обобщение работы [13] на случай фокусировки вихрей с круговой поляризацией и топологическими зарядами, равными ±1 [14], ±2 [14, 15] и ±3 [15]. Отрицательные значения продольной компоненты S z также наблюдались в статье [16], где рассматривались пучки Гаусса–Лагерра с круговой поляризацией и статье [17], где рассматривались пучки Вебера.

В данной работе моделируется острая фокусировка цилиндрических векторных пучков высоких порядков. Было показано, что в фокусе имеют место области, в которых направление вектора Пойн-тинга противоположно направлению распространения пучка. При этом если порядок пучка равен двум, то область отрицательных значений осевой проекции вектора Пойнтинга расположена в центре фокусного пятна.

Теоретическое обоснование

Интегралы Ричардса–Вольфа имеют вид [12]:

.г а 2п

U ( р , v , z ) = - if f f B ( 0 , ф ) T ( О ) P ( О , ф ) х

¹ 00 0                                      (1)

х exp { ik [р sin 0 cos ( ф- v ) + z cos 0] } sin 0 d 0 d ф ,

где U (ρ, ψ, z ) – напряжённость электрического или магнитного поля, B (θ, φ) – электрическое или магнитное поле на входе широкоапертурной системы в координатах выходного зрачка (θ – полярный угол, φ – азимутальный), T (θ) – функция аподизации линзы, f – фокусное расстояние, k = 2п / X - волновое число, X -длина волны, а - максимальный полярный угол, определяемый числовой апертурой линзы (NA = sin а ), P (6, ф) - матрица поляризации, для напряжённости электрического и магнитного полей имеющая вид:

P ( 0 , ф ) =

1 + cos ² ф ( cos 0- 1 ) sin ф cos ф ( cos 0- 1 ) - sin 0 cos ф

sin ф cos ф ( cos 0- 1 ) 1 + sin ² ф ( cos 0- 1 ) - sin 0 sin ф

I 0, m

2, m

a ( 0 , ф ) +

b ( 0 , ф ) ,

где a (θ, φ) и b (θ, φ) – функции поляризации для x - и y -компонент напряжённостей фокусируемого пучка. Для азимутальных пучков высоких порядков функции поляризации будут иметь вид:

E ( 0 , ф )

fa (0, фр vb (0, Ф)?

'" sin ⁽ m ^ф)> _v cos ( m ф ) .

для напряжённости электрического поля и

H ( 0 , ф ) =

f a (0, фр v b (0, Ф)?

^{f- cos (} m ^ф)) _v - sin ( m ф ) .

для напряжённости магнитного поля, где m – положительное целое число. При m = 1 формулы (3), (4) будут описывать обычный азимутально-поляризованный свет.

Подставив формулы (3) и (4) в (1), с учётом (2), можно получить все шесть проекций векторов напряжённости электрического и магнитного полей в области фокуса апланатической системы (функцию аподизации линзы выберем в виде T ( 0 ) = cos^1/2 0 ):

E x = i^{m + 1} [ sin m ф I o, _m + sin ( m - 2) ф 1 2, _m -2 ] ,

E y = i^{m + 1} [- cos m ф 1 0, m + cos( m - 2) ф 1 2, m -2 ] ,

E z = - 2 i^m sin ( m - 1) ф 1 1, m -1 ,

H x = i^{m + 1} [ cos m ф 1 0, m + cos ( m - 2) ф 1 2, m -2 ] ,

Н y = i^{m + 1} [ sin m ф 1 0, m - sin ( m - 2) ф 1 2, m -2 ] ,

H y = - 2 i^m cos( m - 1) ф 1 1, _m -1 ,

где

p а

= 21 f sin 0 cos ¹/² 0 (1 + cos 0 ) x

'-.

X A m (0)e^{ikz cos 0} J m ( x )d 0 , .2 = 21 а sin 0 cos ¹/² 0 (1 - cos 0 ) X

X A m ( 0 )e ^{ikz cos 0} J m -2 ( x )d 0 , I _lm.^^ f ^а sin ² 0 cos ¹/² 0X

’        10

X A m (0)e^ikz cos ⁰ J m ( x )d 0 .

В (6) x = kr sin θ, J m ( x ) – функция Бесселя m -го порядка, A m (θ) = B (θ, φ) – действительная функция, описывающая амплитуду входного поля в плоскости входного зрачка апланатической системы, зависящая только от угла θ и от порядка m поляризационной сингулярности. Из (5) можно получить выражения для компонент векторов электрического и магнитного поля в цилиндрической системе координат:

E r = i^{m + 1} sin( m - 1) ф[ 1 0, m + 1 2, m -2 ] ,

E ф = i m ^{+ 1} cos ( m - 1) ф [- 1 0, m + 1 2, m -2 ] ,

E _z = - 2 i^m sin( m - 1) ф 1 1, _m -1 ,

H r = i^{m + 1} cos ( m - 1) ф[ 1 0, m + 1 2,m -2 ] ,

Н ф = i^{m + 1} sin( m - 1) ф[ 1 0, m - 1 2, m -2 ] ,

H y = - 2 i^m cos ( m - 1) ф 1 1, _m -1 .

Из (7) при m = 1 следуют хорошо известные выражения для компонент поля с азимутальной поляризацией [1]

E ф = 1 0,1 - 1 2,-1 =

= ^ ^ f I" sin 0 cos ^1/2 0 A ( 0 ) J i( x )d 0 ,

¹ 0

H r = ^-[ I 0,1 ⁺ I 2,-1 ] =

= - 2f- f sin 0 cos ^3/2 0 A ( 0 ) J i( x )d 0 , 1 ₀

^Hz = ^{- 2} iI 1,0 =

= - 2 7 ^ / ;а sin ² 0 cos ^1/2 0 A ( 0 ) J _o ( x )d 0 . 1 ₀

В частности, из первого уравнения (8) следует, что в фокусе пучка с азимутальной поляризацией на оптической оси интенсивность равна нулю, так как J 1 ( x ) =0 при x =0.

Из (5) получим выражение для интенсивности электрического поля в плоскости фокуса z =0:

I m = E x I ⁺ | E y | ⁺ | E z | = I 02,m ⁺ I 2, m -2

- 2 1 0, m l 2, m -2 cos [ 2( m - 1) ф ] + 4sin ² ( m - 1) ф 1 1² _m -1

Из (9) видно, что при m > 1 распределение интенсивности в фокусе не является радиально-симметричным. Только для азимутальной поляризации при m = 1 из (9) следует, что интенсивность в фокусе имеет вид кольца:

I 1 - ⁽ I 0,1 ^- I 2,-1 ) 2 .

Из (5) можно получить простое выражение для продольной проекции вектора Умова – Пойнтинга [12]:

S z - 2 Re [ ( E x H * ) z ] - 2 Re ( E x H , - E y H x ) . (11)

В плоскости фокуса ( z = 0) она будет иметь вид:

0, m ¹2, m -2 ^.

Из (12) следует, что при любом m продольная компонента вектора Пойнтинга в плоскости фокуса обладает круговой симметрией относительно оптической оси. Это странный результат, учитывая, что распределение интенсивности в плоскости фокуса (9) не обладает круговой симметрией при m > 1. Из (12) при m =2 в плоскости фокуса на оптической оси имеет место обратный поток световой энергии (при любой действительной амплитуде в плоскости входного зрачка A (θ)):

S 2 ( Г - 0, z ) -

Гл f ^a

-- — J sin 9 cos ¹/² 9 (1 - cos 9 ) A ( 9 )d 9

Также из (12) следует, что при m =3 на оптической оси в плоскости фокуса поток энергии нулевой ( S_z =0), а вблизи оптической оси он по модулю растёт

квадратично с расстоянием от оси:

S з ( r - 0, z ) -

-

( kr ) ² 4

x

a ^f 4

sin ² 9 cos ¹/²

У

9 (1 - cos 9 ) A ( 9 )d 9

Заметим, что, если в предыдущих формулах функцию аподизации зрачка T (θ) = cos^1/2θ заменить на любую другую действительную функцию, например, на функцию аподизации дифракционной линзы T (θ) = cos^–3/2θ [18], уравнения (13) и (14), доказывающие наличие обратного потока в фокусе поляризационного вихря, по форме не изменятся. Изменится только конкретная величина интегралов в (13) и (14). Можно также сказать, что утверждения о наличии обратного потока энергии в фокусе апланатической системы при m =2,3 верны при любой действительной функции T (θ).

Моделирование по формулам Ричардса–Вольфа

В работе моделирование было проведено двумя способами: через вычисление интегралов Ричардса– Вольфа в среде Matlab и решением уравнения Максвелла методом FDTD, реализованным в программном обеспечении FullWave.

На рис. 1 показано направление поляризации в исследуемом пучке порядка m =2.

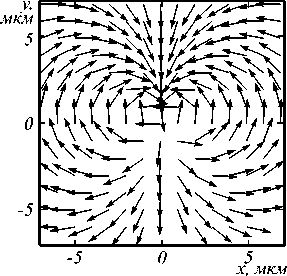
Рис. 1. Направление поляризации в азимутально-поляризованном пучке второго порядка

Для простоты вычислений в моделировании считалось, что зонная пластинка ( T (θ) = cos^–3/2 θ [18], NA = 0,95) фокусирует плоскую волну B (θ, φ)= 1.

Продольная составляющая вектора Пойнтинга вычислялась как

S z - 2 Re [ ( E x H * ) z ] - 2 Re ( E x H y, - E _y H* * ) , (15) а интенсивность – как I = ( EE ^*), где E и H – вектора напряжённости электрического и магнитного полей, Re(.) – действительная часть числа.

Результаты фокусировки азимутально-поляризованного пучка второго порядка m =2 приведены на рис. 2–5. На рис. 2 показано распределение интенсивности света в фокусе (плоскость xy ).

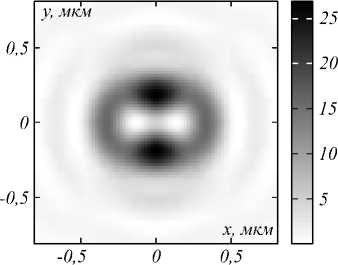
Рис. 2. Распределение интенсивности в фокусе (m = 2): I = I x + I y + I z

Из рис. 2 видно, что распределение интенсивности в фокусе имеет вид асимметричного кольца. Наличие асимметрии объясняется перераспределением энергии между отдельными компонентами электрического поля вследствие острой фокусировки (рис. 3).

На рис. 4–5 показано распределение в плоскости фокуса продольной составляющей вектора Пойнтинга S z : на рис. 4 показано распределение S z в поперечной плоскости ( xy ), а на рис. 5 – в продольной плоскости вдоль оси распространения пучка ( zy ).

Интересно, что в отличие от фокусировки вихря с круговой поляризацией в [15] в данном случае в плоскости фокуса отсутствуют поперечные составляющие вектора Пойнтинга S_x и S_y .

На рис. 6 показаны сечения проекции вектора Пойнтинга S z при фокусировке азимутально-поляризованных пучков c порядками m , равными 1, 2, 3 и 4.

Из рис. 6 видно, что при фокусировке азимутально-поляризованного пучка (m = 1) отрицательных значений вектора Пойнтинга в центре фокусного пятна не наблюдается (Sz (x = y =0)=0). Если же порядок больше двух, то область минимума отрицательных значений проекции вектора Пойнтинга имеет вид ко- лец. При этом в центре фокусного пятна в этом случае проекция вектора Пойнтинга также равна нулю. Только в случае m =2 минимум отрицательных значений проекции вектора Пойнтинга на оптическую ось наблюдаются в центре фокусного пятна (Sz (x = y =0)<0).

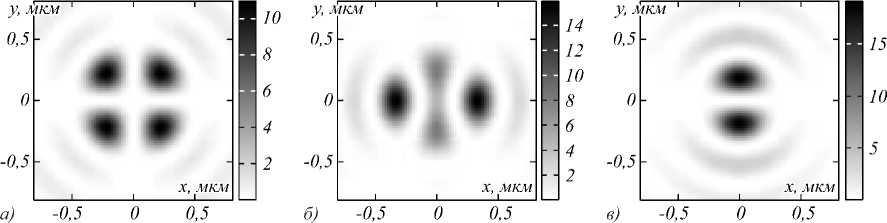
Рис. 3. Распределение отдельных составляющих интенсивности в фокусе: Ix (a), Iy (б) и Iz (в). Суммарная интенсивность I показана на рис. 2

-0.5         0        0,5

Рис. 4. Распределение продольной составляющей вектора Пойнтинга Sz в фокусе (m = 2)

-2 -10  12

Рис. 5. Распределение продольной составляющей вектора Пойнтинга в плоскости yz (m = 2)

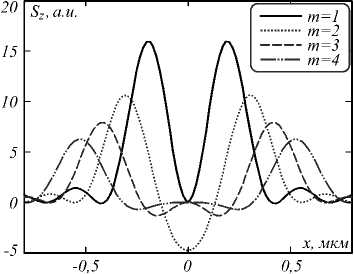
Рис. 6. Распределение продольной составляющей вектора Пойнтинга Sz в фокусе зонной пластинки при фокусировке азимутально-поляризованных пучков порядка m = 1, 2, 3 и 4

На рис. 7 показана зависимость минимального значения Sz в центре фокусного пятна от числовой апертуры NA для азимутально-поляризованного пуч- ка порядка m =2. Из рис. 7 видно, что отрицательные значения Sz проявляются только при больших значениях числовых апертур (NA>0,8).

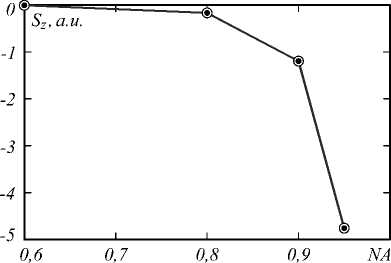
Рис. 7. Зависимость минимального значения Sz в центре фокусного пятна от числовой апертуры NA для азимутально-поляризованного пучка порядка m = 2

Моделирование с помощью FDTD-метода

Метод FDTD использовался для качественной проверки результатов, полученных с помощью интегралов Ричардса–Вольфа. Методом FDTD, реализованным в программном обеспечении FullWave, рассматривалась фокусировка плоской волны, умноженной на функцию пропускания зонной пластинки Френеля. Функция пропускания зонной пластинки рассчитывалась из соображений, что её фокусное расстояние равно 532 нм, а фокусируемый свет имеет длину волны 532 нм, высота рельефа h = 0,159 мкм, показатель преломления материала n =2,67 (TiO 2 ). Так как ставилось целью только качественное сравнение результатов, полученных разными методами, то числовая апертура такой линзы не подбиралась равной числовой апертуре линзы, моделируемой по формулам Ричардса–Вольфа. Шаг сетки вдоль всех координат считался равным λ /30. Размеры рассчитываемой области 8,6×8,6×1,532 мкм. На краях вычисляемой области помещались идеально согласованные слои (PML) толщиной 0,5 мкм.

Из рис. 8 видно, что в центре фокусного пятна наблюдаются отрицательные значения S z , таким образом, результаты, полученные с помощью метода

FDTD качественно подтверждают результаты, полученные с помощью формул Ричардса–Вольфа.

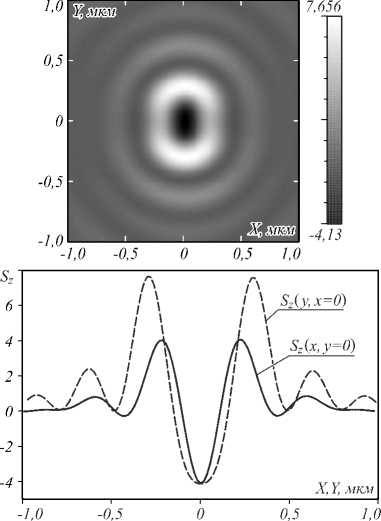
Рис. 8. Распределение продольной составляющей вектора Пойнтинга Sz в фокусе зонной пластинки, вычисленное с помощью метода FDTD

Заключение

В данной статье моделировалась острая фокусировка цилиндрических векторных пучков высоких порядков. Теоретически и численно показано, что в фокусе наблюдаются области, в которых направление вектора Пойнтинга противоположно направлению распространения пучка. При этом если порядок пучка равен двум, то минимум отрицательных значений проекции вектора Пойнтинга расположен в центре фокусного пятна.

Возможность получения фокусных пятен, в которых вектор Пойнтинга противоположен по направлению распространению пучка, ранее была показана в работах [13–15], однако там фокусировались оптические вихри и поток энергии распространялся по спирали (спиральный обратный поток). В этой же работе обратный поток имеет невихревой характер.

Отметим также, что азимутально-поляризованный пучок второго порядка может быть получен из линейно-поляризованного пучка с помощью одного единственного элемента, преобразующего поляризацию, например, поляризатора на основе субволновых решёток [19].

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Теоретическое обоснование», Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части

«Моделирование с помощью формул Ричардса– Вольфа» и Российского фонда фундаментальных исследований (гранты 17-47-630417, 17-47-630420, 17-42630008, 18-07-01122, 18-07-01380, 18-29-20003) в части «Моделирование с помощью FDTD-метода».