Обратный поток энергии в векторных модах световодов

В настоящее время растет интерес исследователей к распространению в световодах мод с сингулярностями фазы [1 –3] или поляризации [4]. В литературе по световодам данные моды получили название мод с орбитальным угловым моментом (ОУМ-мод), хотя в случае чисто поляризационных вихрей такие моды и не обладают ОУМ. Так как оптические вихри, обладающие разными топологическими зарядами, распространяются в волокне независимо друг от друга, их использование видится перспективным для уплотнения сигнала [5], где отдельный топологический заряд вихря отвечает за отдельный канал связи.

Для распространения ОУМ-мод используются волокна разных типов [6]: например, волокна с градиентным изменением показателя преломления сердечника [7], капиллярные волноводы [8– 10]. Но в основном наблюдается рост использования для этих целей микроструктурированных волокон, работающих на основе принципа фотонно-кристаллической запрещенной зоны [11 – 16].

Следует отметить, что интересным эффектом высших мод, обладающих сингулярностью фазы и/или поляризации, является наличие в них областей, в которых направление потока энергии противоположно направлению распространения пучка (т.н. области обратного потока энергии) [17, 18]. Однако в волноведущих средах этот эффект ранее не исследовался.

В данной работе с помощью программного обеспечения RSoft Fullwave промоделировано распространение цилиндрического векторного пучка второго порядка в градиентном и микроструктурированном волокнах. Показано, что векторные пучки второго порядка являются векторными модами данных волокон. В центре световодов наблюдаются области, в которых поток энергии направлен в сторону, противоположную направлению распространения пучка (области обратного потока энергии).

1.    Потоки энергии основной моды стержневого микроструктурированного волновода

Моделирование в данной работе осуществлялось с помощью программного обеспечения RSoft Fullwave, в котором реализован расчет прохождения света через объекты микрооптики методом FDTD. Для расчета основной моды световода с заданным распределением показателя преломления использовалась встроенная в программу подпрограмма, которая итерационным методом рассчитывает основную моду на основе некоторого начального условия (в частности, с помощью начального условия задается именно векторный характер моды). В качестве пучка, заводимого в световод, использовался цилиндрический векторный пучок второго порядка, вектор Джонса которого равен:

"- sin ( 2фр cos ( 2 ф )

где φ – азимутальный угол в цилиндрической системе координат, выбранной таким образом, что ось z совпадает с направлением распространения пучка. Ранее нами было продемонстрировано, что именно для второго порядка векторного пучка на оси возникают отрицательные значения для продольной проекции вектора Пойнтинга [18].

В качестве первого исследуемого световода рассматривался стержневой световод [19], состоящий из шести стержней с радиусами r = 0,684 мкм, расположенными вдоль окружности с радиусом R = 11,4 мкм (рис. 1), длина волны света λ = 1 мкм. Показатель преломления оболочки считался равным 1,45 (кварцевое стекло), показатель преломления стержня был равен 1,478 (допированное германием кварцевое стекло [19]). На краях расчетной области в моделировании помещались идеально согласованные слои (PML) толщиной в одну длину волны распространяющегося в световоде излучения. Параметры поглощающих слоев подбирались таким образом, чтобы минимизировать отражение от границ расчетной области.

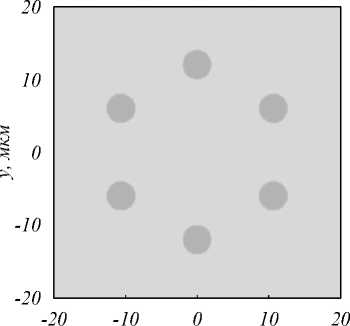
x, мкм

Рис. 1. Профиль моделируемого световода

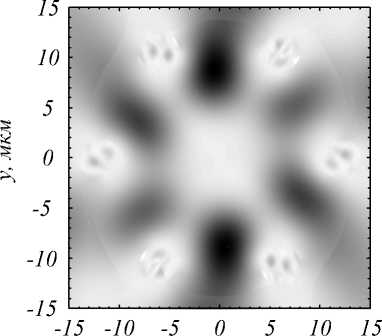
На рис. 2 показано направление напряженности электрического поля основной моды, подтверждающее сохранение состояния поляризации в ней после распространения в волноводе. Распределение продольной составляющей вектора Пойнтинга S z в вычисляемой области показано на рис. 3: S z =Re ([ E × H *] z ). На рис. 4 для наглядности отдельно показаны зоны, в которых проекция вектора Пойн-тинга на оптическую ось отрицательна.

-2

-4

-6

-6 -4 -2 0 2 4 6

x, мкм

Рис. 2. Направление поляризации основной моды стержневого волокна

1.5

0.5

x, мкм

Рис. 3. Распределение продольной проекции вектора Пойнтинга в стержневом волокне

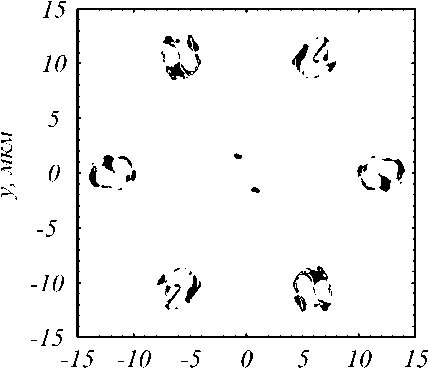
X, мкм

Рис. 4. Области обратного потока энергии в рассчитываемом стержневом световоде. Черный цвет соответствует обратному потоку, белый – прямому

Из рис. 3–4 видно, что в центре световода (две области) и рядом с отдельными стержнями формируются обратные потоки энергии (проекция вектора Пойнтинга на ось z принимает отрицательные значения). Стоит отметить, что абсолютная величина проекции вектора Пойнтинга в областях обратных потоков мала, эта малость является ожидаемой, так как большие значения обратного потока проявляются только в условиях острой фокусировки [18].

2.    Потоки энергии основной моды кольцевого микроструктурированного волновода

Рассмотрим далее похожий микроструктуриро-ванный световод. Данный световод представляет собой центральный стержень с диаметром 32 мкм, окруженный стержнями меньшего диаметра (12,5 мкм). Профиль рассчитываемого световода показан на рис. 5, показатель преломления оболочки считался равным 1,45, а показатель преломления стержней был равен 1,478, длина волны света λ = 1,55 мкм. Ранее похожая структура световодов предлагалась для передачи ОАМ-мод [11, 12, 20].

На рис. 6 показано распределение продольной проекции вектора Пойнтинга (рис. 6 а ) и области, в которых она принимает отрицательные значения (рис. 6 б ). Рис. 6 также подтверждает сохранение обратных потоков энергии в световоде (рис. 5).

а)

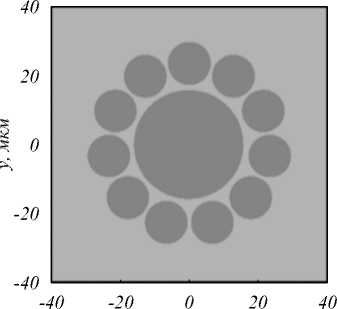
x, мкм

Рис. 5. Профиль моделируемого световода

1,5

-2

-2

-4

-6

-4

x, мкм

0,5

X, мкм

б)

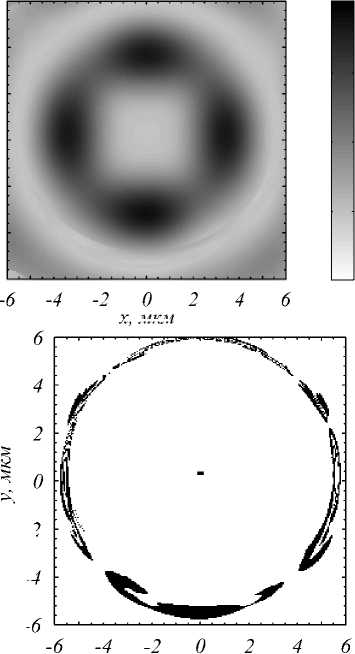
Рис. 6. Распределение продольной проекции вектора Пойнтинга (а) и области обратного потока энергии (черный цвет) (б) в рассчитываемом кольцевом световоде

3.    Основная мода градиентного волокна

Рассмотрим теперь основную моду световода с сердечником, показатель преломления которого изменяется в соответствии с формулой [21]:

n ( r ) = n 0

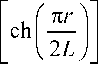
где n0 – показатель преломления линзы на оси, r – радиальная координата, L – полупериод схождения лучей (в таком градиентном световоде свет периодически собирается на оси). Ранее нами было продемонстрировано, что отдельный кусок такого волокна (градиентная линза) способен фокусировать цилиндрический векторный пучок или оптический вихрь вблизи своей выходной поверхности, формируя изо- лированную от свободного пространства область обратного потока энергии [22].

В моделировании считалось, что n 0 =3,47 (кремний), L = 10 мкм, радиус сердечника R =9,33 мкм из соображений n ( R )= 1,5, длина волны света λ = 1,55 мкм. Моделирование осуществлялось с помощью FDTD-метода, реализованного в программе Fullwave (шаг сетки по пространству 0,01 мкм = λ /155).

x, мкм

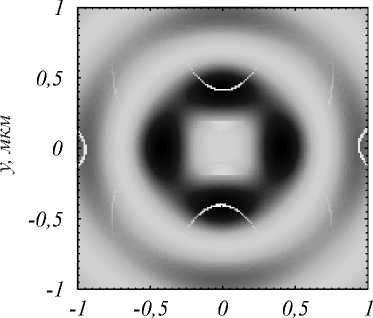
Рис. 7. Распределение продольной составляющей вектора Пойнтинга S z в вычисляемой области

Из рис. 7 видно, что и в данном случае в сечении пучка содержатся области, в которых продольная проекция вектора Пойнтинга отрицательна. Отметим, что возникающие отражения на рис. 7 могут быть вызваны недостаточно хорошим подбором параметров идеальных поглощающих слоев (PML).

Заключение

В данной работе с помощью программного обеспечения RSoft Fullwave промоделировано распространение цилиндрического векторного пучка второго порядка в двух типах микроструктурированных (стержневой и кольцевой) и градиентном световодах. Моделирование показало, что векторные пучки второго порядка являются векторными модами данных волокон. В вычисленных основных модах данных световодов наблюдались области, в которых поток энергии направлен в сторону, противоположную направлению распространения пучка (области обратного потока энергии). Абсолютная величина продольной составляющей потока энергии была мала.

Работа выполнена при поддержке Российского научного фонда (проект № 22-22-00575).