Образование субзеренной структуры в деформируемом кристалле как в континууме Коссера

Equations were proposed to describe developing of fragmented subgrain pattern in crystalline body under large plastic deformations. Cosserat continuum mechanics was discussed and used. The model is geometrically nonlinear, that induces instability of material in form oj cellular pattern with certain symmetry and characterictic size. During transition from one cell to neighbour the lattice spin changes smoothly its sign that permits us to treat these cells by subgrain embryons.

При развитых пластических деформациях в металлическом кристаллическом теле образуется субзеренная структура [1]. В ходе квазистатического деформирования равновесие материала в области с однородно ориентированной кристаллической решеткой становится неустойчивым и развивается продолжение процесса с пространственно-модулированной структурой разориентаций решетки. Довольно простая модель, описывающая такие тенденции, может быть построена на основе континуума Коссера, точка которого снабжена спином, а уравнения содержат комплекс размерности длины. Используются инкрементально-линейные уравнения состояния, но при этом учитываются эффекты геометрической нелинейности, играющие важную роль в напряженной конфигурации твердого тела. Предпринята попытка описать явление средствами механики при достаточно простой физике, ограниченной линейным определяющим уравнением (не сложнее закона Гука) с положительно определенным тензором касательных модулей, без использования ниспадающих диаграмм и фазовых переходов.

Аппарат

Доступным пособием, в котором приводятся все уравнения континуума Коссера. является [2]. Здесь мы только напомним и поясним идеи, лежащие в основе этого континуума, без вывода уравнений, то есть дадим некоторые необходимые комментарии.

Иногда существенно, что среда состоит из частиц, размер которых конечен. Это влечет принципиально отличное описание движения среды, поскольку теперь она состоит не из материальных точек, а из точек-тел, способных вращаться [3]. Рассмотрим простейшую точку-тело, состоящую из двух материальных точек, соединенных жестким невесомым стержнем (рис. 1). Масса системы определяется как- т = ^та fa = 1,2), центр масс - ^ --^^таха , скорость центра масс - v = — ^mr,v(, . a                                “ радиус-векторы и скорости материальных точек тогда представимы как х =х + х' v =v+v' Количество движения системы запишется как Q = ^mava-mv, главный вектор действующих на нее сил - F = ^fa, момент о.                                                                                                                                a количества движения - L = '^тиха х vo = тх х v + ^/я„х^ х v^,= хх Q + I. главный момент сил - M = ^xaxfa=xxF + ^x^xfa=xxF + k. Векторы i и к суть собственные моменты количества движения и сил. Законы инерции для системы имеют вид

Q = F, L M mN = F , 1 = k .

(' )

или в эквивалентной форме

Эти законы независимы, но следуют из закона инерции материальной точки т₍л_о = f^

fXa = 1,2), примененного к точкам системы. Для малой системы 1« xxQ, k « хх F. поскольку 1 и к содержат ее характерный размер. Отсюда второй из законов инерции (1) имеет дело с малыми величинами по сравнению с величинами в первом законе. Это оправдывает гипотезу 1 = к г О, лежащую в основе безмоментного континуума. Однако важно понимать, что характерный размер мал, но конечен, и иногда это принципиально важно. Явным носителем размера выступает уравнение (1)2. Поскольку система жесткая, можно определить ее момент инерции J и угловую скорость со. так что 1 = J со и (1)2 принимает вид J ю = к . Характеристики системы т, J, v, о, F, к относят к геометрической точке х радиус-вектора центра масс, затем в объеме, заполненном такими изолированными точками-телами, выполняется континуализация полей. Вывод уравнений механики обобщенного континуума из классической механики точки дан в [4]. Исходя из континуальных представлений, эти уравнения вывел автор [5]. Из наших рассуждений вытекает область применимости уравнений континуума Косссра:

гранулированные, зернистые, фрагментированные среды с жесткими частицами и масштабно-зависимым поведением.

Типичные для    континуума   Коссера

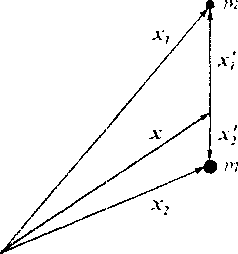
Рис. ЕПросюйшая модель точки-тела

переменные состояния   появляются   уже из формальных энергетических соображений. Скорость совершения работы внешними силами над телом В равна IF = Jv • t/F^ = Jv • <7FL + Jv ■ d¥BXX в терминах в          в          в

• [6] . Обозначим Jv • dY^ = Р .В инерциальной системе в

  отсчета

  
  

  <№_в.^ ⁼ ~^^т_в

  
  

  откуда

  
  

v • t/F^.v = --^ Jy v • NdmB = -Т . Если U - внутренняя в                 в энергия тела В, то первое начало термодинамики в адиабатическом приближении утверждает равенство

U = ^f, в инерциальной системе отсчета принимающее вид U = Р-Т. Если с - удельная внутренняя энергия, turn- контактные силы и пары, j - дистанционные пары, то в общем случае континуума Коссера m Ф 0. j * 0, to * 0, [а] * 0, U = [сЧДд, в

Р = jt ■ v + m ■ о dSB + jf • v + j- co dVB , T = Jy(pv - v + co J to) dVB , откуда в силу в                     в                         в уравнений движения V а + f = pv, V-p-€:o + j = J to, выполняющихся внутри тела, и соотношений Коши t = n а, ш=п ц на его границе можно получить выражение U = а: (vV - Q) + ц: coV (Я = -Есо). Поэтому в качестве переменных состояния удобно принять vV -Q, coV и не зависящие от системы отсчета скорости о и ц , если рассматриваются инкрементально-линейные определяющие соотношения. В таком континууме уравновешены дистанционные моменты-пары j, контактные моменты-пары m (р) и моменты контактных сил (несимметричная часть а), действующие на объем. Можно рассмотреть континуум без контактных моментов-пар m - 0, j * 0. со* 0, [о] * 0, для которого L/ = o:(vV-ti), а определяющие соотношения связывают vV - Q и не зависящую от системы отсчета скорость о . Модель, в которой дистанционные моменты-пары уравновешены моментом контактных сил, использовал автор [7]. Если при этом, как в [8], со г О , то U = о: vV, а зависящие от системы определяющие соотношения связывают vV и скорость а и годятся для малых искажений конфигурации. В безмоментном континууме m - 0, j - 0, со = 0. [о] = 0 , U = о: vV = а: {vV}, а определяющие соотношения связывают {vV} и не зависящую от системы отсчета скорость о. Рис. 2 дает представление о чистых видах искажения представительного объема континуума Коссера. Жесткие квадратные частицы находятся в невесомом связующем, передающем усилия; vV определяется нолем скоростей центров масс частиц, а со и coV - полем их спинов.

Для выяснения смысла переменных состояния и природы связывающих их определяющих соотношений рассмотрим плоскую среду, состоящую из одинаковых круглых гранул (рис. 3). Кинематика гранулы включает' поступательное перемещение и в ращени е.__           _                _

со - 0                 со - 0                     со * 0                  со - 0

Vto=Vv~o       Vto = 0, Vv * 0        Vco = Vv-0        Vco*O, Vv - 0

Рис. 2. Чистые виды искажения объема континуума Коссера

Скорость проскальзывания гранул А и В в точке их контакта х_АВ записывается как-

^ar = Ъ - х_д + ^пт • (^ХАВ - х J - Q_fi ■ (X _АВ -х_в) =

• —    v₄ — n _в — й_А • (х_д — х_я) + (Q_₄ — И_в)' (х_дв —х_в) =

• —    [L - Q^ + Г- (х ^у — Ху)] • (х _д х_в ), где компоненты линейного оператора L = vV однозначно находятся из уравнений

^va “^vb = ^L’(x,<-Хд), х_в-х_с=Ъ\х_в-х_с^          (3)

соответствующих трем контактирующим гранулам (рис. 2), а компоненты линейного оператора Г = QV однозначно находятся из уравнений

^А — ^В ~ Г ' (^ХА — ^ХВ )’ ^В ~ ^С ⁼ Г ' (^х5 — Х_с ) .              (4)

Статика гранулы заключается в ее равновесии под действием сил и моментов-пар, приложенных в точках контакта, причем моменты-пары появляются вследствие конечного размера реальной области контакта. Трем контактирующим гранулам могут быть поставлены в соответствие тензоры напряжений и моментов-пар, например, вида ст = Е1лл®(хл-xs),  ^ = Ет^ ®(Хл-Ху),            (5)

где суммирование производится по точкам контакта трех гранул А. В и С. Определяющие соотношения для представительного объема рис. 3 выводятся из контактного закона в инкрементально-линейном виде

^ЛВ ⁼ ^Н3«^П.4В + ^АВ^АВ ) ' ^ АВ •

С учетом (2), (3), (5)1 и гипотезы Q4 ~QB ~Q имеем с = Б(хл - хя )2 ^двпдвпдвпдв + рт^уТ 4Sn лй)] с (L - О).    (6)

Из контактного закона для моментов-пар в инкрементально-линейном виде rh ti = X(QA -Qs) с помощью (4), (5)2 получаем

4 ⁼ [^/L(Xa ~x_s) n^n^yJ’F.                       (7)

Скорость изменения мощности в представительном объеме имеет вид

U = £[^в ■ v ₄₅ + m_лв о (О._А - П_в )] = а □ (L - й) + ц Г .

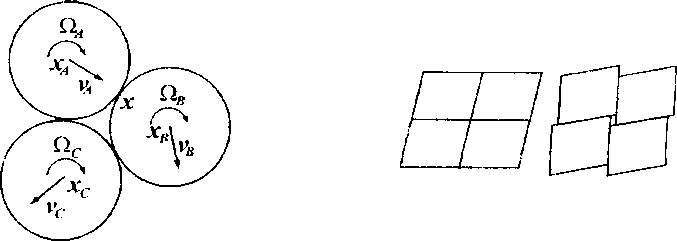
Рис. 3. Представительный объем             Рис. 4. Модель скольжения гранулированной среды                 и поворота жестких блоков

При переходе от t и ш к о и |i считалось, что расположение гранул меняется мало или сравнительно малы величины t и m, что соответствовало геометрически линейной ситуации. Если же это не так, то учет мгновенного искажения локштыгой конфигурации приводит к появлению вместо о и Д некоторых коротационных производных. В случае круглых гранул (см. рис. 3) поворот касательной опредсляеюя вихрем поля линейных скоростей (а не спином) гранул, и мы имеем яуманнову производную. Если частицы есть блоки, скользящие и поворачивающиеся как на рис. 4, то поворот линий скольжения определяется спином блоков, а не вихрем поля их линейных скоростей, и мы имеем спинорную производную. Эти ситуации представляют крайние и, скорее, качественные случаи, в реальных средах вращение линий контакта определяется обоими видами движения.

Модель

Рассматривается несжимаемая среда с инкрементально-линейными свойствами в текущей конфигурации Kt ф1 =Н (Vv + £2) - pl, V • v = 0,                (8)

|Xn=LoVco,                              (9)

где а. ц - несимметричные тензоры истинных напряжений и моментов-пар, a^sd + c Q-Q а - спинорная коротационная производная, H.L полусимметричные тензоры аффинных и изгибных касательных модулей, Vv -градиент скоростей перемещений, £2 - спин, т = —-т€£2 - аксиальный вектор спина, Vco - градиент спина, р - гидростатическое давление, £ - альтернирующий тензор третьего ранга, I, ° - единица и скалярное умножение в пространстве тензоров второго раша, ■ - скалярное умножение в пространстве векторов. Уравнения равновесия в скоростях в терминах т екущего лагранжева подхода имеют вид

V d-Vvr=Va = 0,                    (10)

V ■ ц - Vvr = Уц + £ = 6 = 0.                   (] I)

Соотношения (8),(9) соответствуют упругопластичности при активном нагружении. Коммутатор коротационной производной в (8),(9) и конвективные слагаемые в (10),( 11) отражают вклад геометрической нелинейности, важный в вопросе бифуркации напряженной конфигурации.

Записанные уравнения имеют смысл для представительного объема кристаллической среды в К( с однородно ориентированной решеткой и доменным строением. Объем реального кристалла, как правило, оказывается разделенным на блоки кристаллографическими полосами скольжения или на ячейки дислокационными стенками. В такой разбитой на домены среде и рассматривается образование зеренной (субзеренной) структуры с характерным размером, много большим размера домена. Если считать, что в текущий момент времени каждый домен может перемещаться и поворачиваться как жесткое целое под действием сил и моментов-пар, приложенных по поверхностям контакта с соседними доменами, то в гладком представлении такая среда будет являться континуумом Коссера и при некоторой детализации контактных взаимодействий подчиняться уравнениям (8)-(11). Жесткость домена влечет вмороженность в него решетки, и балансовое уравнение моментов выступает в качестве полевого уравнения спина решетки. Без этой гипотезы необходимо строить локальную декомпозицию движения решезки/магериала и полевое уравнение для спина решетки. Уравнения (8),(9) выводятся, как для гранулированной среды [71. При этом домены отождествляются с блоками, что приводит к появлению спинорной корогационной производной тензоров напряжений. В конце будут приведены результаты для яуманновой производной — другого частного случая доменной структуры. За изгибы структуры могут отвечать дисклинации кристаллической решетки на краях доменов.

Бифуркации в среде

Рассмотрим равновесие неограниченной плоской среды с однородно распределенными материальным свойствами под действием однородного поля сжимающего напряжения ст22 =-а (а>0) вдоль оси е2 ортобазиса е( а -1.2,. Тогда С = ОТ, ц = 0, V есть собственные векторы тензора о. сам он имеет ортотропную симметрию с осями ек д-гз?, уравнения (8)-(11) становятся линейными с постоянными коэффициентами. Пусть тензоры Н и L положительно определены и обладают кубической симметрией с осями вдоль еА 12,. Тензор H = /7,,h,h, в ортобазисе h, --^(6,6, -е2е2), h, = -^-(е,е2 + е2е,), h3 = -^-(е,е2 -е2е|)

тогда имеет ненулевые компоненты Н кк = ц* >0 ^ = 1,2,3), а тензор L = /..,h,h, в ортобазисе h4=e,e3, h5=e2e3 - ненулевые компоненты LusX>0 d, =

Положительная определенность этих тензоров соответствует восходящему участку зависимости истинных напряжений от деформаций. Система (8)-(Н) в терминах функции тока v, = ф,₂, v₂ = -р^ и скаляра (»=0), после исключения р принимает вид

f(p2 +Ц3)^1Ш + 2(2р, -р, + Ц3)Ф,1-22 +(р2 +М3Ж222 +

<                                        +2(с + ц3 )и22 - 2(о - Цз )сщ 0.     (12)

ХА® - Рз (2® + Аф) - 0.

Во втором уравнении системы может быть выделен комплекс

Л 2ц;

размерности [м ],

являющийся квадратом характерного масштаба ее просгранственно-модулироваппых решений.

т

При исчезающе малых значениях из (12) следует, что спин решетки сводится к материальному вихрю, решеточная коротационная производная — к яуманновой производной, а уравнение для ф принимает вид

[ц2 +о]ф1Ш + 2(2^ -ц2]ф.:22 +[Ц2 -0X2222 -О               (13)

и утке исследовано в [9].

Найдем нетривиальные ограниченные на бесконечности решения системы (12) в форме ф = Ке[ф0 cxp(z к • х)], to = Re[®c ехр(г к • х)]                  (14)

и условия их существования. В (14) к - вещественный волновой вектор, i - мнимая единица, фр, top - комплексные амплитуды. Линии kx-t const, к - к называются характеристиками. Вектор к = к,е, удобно представи гь как £,.=£{-sin 8, cos 5}. >■ 12. где 5 - угол ориентации характеристики относительно е,. Подстановка (14) в (12) ведет к условию бифуркации ст = (ц2 - ц 1 )(1 + to cos 25 + (ц, + (ц3 + ц,)          7.

-Вз                       +Из cos 2d

При ц2 < 2ц, (сюда входит и случай изотропии ц2 = ц,) появляется горизонтальная характеристика при напряжении д* = ц2. При ц2 > 2ц, в момент д, = 2^Дц? -Ц])Ц| появляется пара характеристик под углами ±8», где s 1 Г Щ о, = — arccos J-n—

2      \ Ц2~Ц|

< тс / 4. В момент бифуркации = 0, и если тЛ-

* 0. то к = 0 и

2Ц3             2Ц3

мы имеем тривиальное решение. При напряжениях же выше критического появляются нетривиальные решения. При ц2 < 2ц, и g > д’ угол наклона характеристики заключен в отрезок [—S_,5_J, где

8+

= — arccos 2

g±Va² -4(ц₂ -ц^ц, 2(ц₂ - ц,)

I 5+ |<

л

4’

причем, возможна и симметричная пара характеристик. При ц2 > 2ц, и д, < g < g углы наклона симметричной пары характеристик заключены в отрезки [—5_,—5. ].

[8+,3_]. В момент g = g' эти отрезки соединяются в один [~8_,8_]. По мере неограниченного роста g границы этого отрезка монотонно стремятся к ±^. Условие

л

2ц3 '

бифуркации и наклон линий не зависят от

Механизмом дестабилизации материала является геометрическое разупрочнение за счет локального поворота осей анизотропии. В случае -А- = 0 при критическом напряжении материал становится неустойчивым, оператор равновесия (12) теряет строгую эллиптичность и приобретает характеристики, при этом профиль решения вдоль k/Х не определяется оператором и может быть произвольным [10]. При -^- >0 смены режима оператора в момент бифуркации не происходит. Потеря устойчивости материала выражается в появлении характеристик и модулированного (а не произвольного) профиля решения вдоль к /к. Характеристики симметричны относительно осей е_к ц = 1,2у, ибо оператор (12) имеет ортотропную симметрию.

определяемую пересечением групп симметрии тензоров Н, L и g .

Определение волнового вектора

При надкритическом напряжении любому 8 из допустимого интервала соответствует свое волновое число к. Из множества допустимых волновых векторов следует найти такое, которое бы обладало некоторыми экстремальными качествами. Энергетические соображения для решения этой проблемы использовать не удается, поскольку система (12) не является консервативной. Можно показать, что не существует квадратичной функции, уравнения Эйлера-Лагранжа для которой давали бы (12). Существо дела заключается в коротационной производной определяющих соотношений: единственной коротационной производной, которая может присутствовать в инкрементально-линейных соотношениях, связывающих энергетически сопряженные тензоры, является яуманнова производная [11]. Здесь

Qsi(vV-Vv) возможно только при т+у- = О, то есть в безмоментном случае.

Согласно [12] построенная нами система является циркуляционной, а последние часто встречаются среди механических устройств с вращательными степенями свободы. Единственным надежным методом исследования их устойчивости является динамический метод.

Динамика склерономной системы связывается с ее инерционностью, поэтому в правые части уравнений (12) добавляются соответственно рАф и Jto, а решения разыскиваются в виде ф = Ке[ф0 ехр(/ к х т w?)], со = Re[con ехр(/ к х + нт)]

где w - комплексная скорость. Условие существования нетривиальных решений рУш + ГрГХ^^ 4* 2g3) + JAk" ]w* + (Хк +2Цз)У^ ™2g3(c?cos28 + g3)^ — О, где А = (g2 + g3)sin4 8 + 2(2g, - ц2 + g3)sin2 8 cos" 8 + (g2 + g3)cos4 8 , представляет собой биквадратное уравнение, корни которого э -с ± уей - 4рУс/ мф =----------------,

- 2рУ где с = р(ХФ2 + 2ц3) + ААк2 -р(Хк2 + 2g3) +Л2[(р2 -g,)cos2 28+ g, -gj > 0

d = (Хк² + 2g₃)[(g₂ -gjeos² 28+ g, + g₃]£² -2g₃(ocos28 + g₃U² =

= Х[(ц₂ - g,)cos² 28+ g, + g₃]A" + 2g₃[(g₂ -g, )cos" 28- о cos 28 + р, \к~.

При переходе О через критическое значение знак d меняется с положительного на отрицательный. Независимо от значения о дискриминант с2 - 4рФФ = {р(?Лг2 + 2g3)-J£2[(g2 -gjeos2 26 м1, -Ц?]}2 +8pJg,(ocos28 + u5 У-положителен. Сценарий динамического поведения системы таков. При некритических <5 иф < 0 и единственное тривиальное продолжение процесса устойчиво. При критическом ст            =—— и при ограничениях, запрещающих жесткое движение, имеем аналогичный результат. Наконец, при надкритическом о ну >0. му <0 и развивается потеря устойчивости в форме отклоненного решения (14). На комплексной плоскости первая пара сопряженных корней движется но мнимой оси к нулю и, встретившись, уходит от него вдоль вещественной оси. Вторая пара сопряженных мнимых корней при этом постоянно удаляется от пуля. Такая форма потери устойчивости является статической и соответствует дивергенции [12],

Отклоненное решение при надкритическом значении бифуркационного параметра образует пара волновых векторов, соответствующих максимальной скорости роста |ш+|- Эти волновые векторы удобно представить через к\ ,8, : k, = A,{sin5,, cos8„], к, = 4. {-sin 8,, cos8»}. Для поиска ^,84, (или к,. х. = cos 28.) / ^                  2 pJd -■ d ограничимся малыми надкритичностями, когда ^е' - 4pJd -с-----— и ну =---

С                 V

Поскольку |с/|«с, a c>2pg3>0 при лзебом к" >0, максимум функции иф(А-.л-> приближенно соответствует максимуму функции -d(k,x). Экстремум находится из алгебраических уравнений х = ИзО , к2 С^-ф^-^ + Ф

(ц2-pJfXA:2 + 2ц3)’ X ф,-ц^х2 + ф + ц3'

Данная система сводится к

(ц2 -Ц.^х3 + ф2 -2ц3)х-оф1 -Ц3) = 0(16)

и (15)₂. В случае ц₂ > 2ф при о* < о < о* к² неотрицателен на отрезке хе [x_,xj (где х_т = cos28_±) и принимает на нем свое наибольшее значение в точке локального экстремума. При ос* независимо от соотношения ц, и ц₂ X² неотрицателен на отрезке хе [х_,1] и достигает наибольшего значения в точке локального экстремума или на границе х = 1. Из (15),( 16) следует, что изгибная жесткость решетки X не влияет на наклон характеристики, а определяет волновое число к. Из (15)2 видно, что с увеличением X волновое число уменьшается.

Существуют отклоненные решения системы ячеистого вида. Например, при Ц2 > ц, (16) имеет один действительный корень х*, являющийся положительным. В случае ц, > 2ф и о* < <5 < С * этот корень располагается в допустимых пределах О < х_ < х, < лц < 1. По х* из (15)2 находится к*. В частном случае, когда фу, №<> - вещественные, ф = ф0 [sin(k, ■ х) + sin(k, ■ х)] = 2ф0 cost/:* sin 8t x;)sin(£, cos 0„ x2).

co = 2coo cos(£* sin ф xs) sin^. cos 8t x2).

Рис. 5 представляет вид этого решения. При переходе из любой ячейки в соседнюю спин решетки меняет свой знак, что позволяет считать данные ячейки «зародышами» субзерен. Бифуркация приводит к разориенгации кристаллической решетки этих ячеек, то есть к фрагментации указанного в начале статьи типа.

При фиксированных модулях упрочнения и надкритическом напряжении характерный размер ячеек растет с увеличением изгибной жесткости решетки. По мере роста надкритичности бифуркационного параметра (все же остающейся малой) имеет место аналогичная тенденция. В этом случае интервал [х. ,х+], а вместе с ним и корень х*, смещаются по направлению к границе х ~ I. При этом ячейки “сплющиваются”.

При исчезновении изгибной жесткости при критическом напряжении согласно (15)2 происходит потеря устойчивости, сопровождающаяся бесконечно большим количеством полуволн нормально к характеристикам. Это означает, что в этот момент материальные точки среды становятся изолированными и начинают свободно уходить от основного состояния со своими

Рис. 5. Структура ячеек с противоположно направленными спинами решетки

начальными скоростями. Странность этой моды потери устойчивости, обнаруженной и в [9], связана с ограниченностью безмоментной модели (13).

При малых надкритичностях Im-cH VAo независимо от скорости изменения о. Поэтому полученные результаты имеют смысл, если нагружение вести со скоростью, все время превышающей |w₊|.

Если в уравнениях (8), (9) использовать вместо спинорной яуманнову производную, го критерий бифуркации примет вид о = (р, - щ) cos25 (ц. + ц3 + —™г) —,

1 । cos 26

2ц3

а условия появления и наклон характеристик в точности совпадут с уже изученным случаем. При ц2 > 2Ц] и п, < 6 < а’ реализуется продолжение процесса с допустимыми параметрами, v °     а-2 = - С? -4p!(p2 -uj

2(Р~-Щ)’       ^ а2fp.,)

Описанные выше качественные особенности решения остаются прежними.

Принципиально важным для описываемого эффекта оказался учет геометрической нелинейности (способной вызывать геометрическое разупрочнение и потерю устойчивости материала) в сочетании с нелокалыюстью модели г-в длинноволновом приближении»), И то, и другое естественным образом, без введения новых переменных и формулировки дополнительных уравнений, оказалось в наличии в континууме Коссера.

Работа выполнена при финансовой поддержке РФФИ по проекту 01-01-00440.