Образовательно-трудоохранная интерпретация задач математического программирования на поиск минимума целевой функции

Предположение о том, что все актуальные в контексте некоторой человеческой деятельности опасности можно выявить и полностью устранить, отвергается - таково содержание аксиомы о невозможности полной безопасности . Например, пользование электроосветительными приборами для человека представляет опасность. Наивная попытка ее полностью устранить привела бы к использованию в целях освещения еще более опасных устройств: свечей, керосиновых ламп, газовых горелок и тому подобного.

Признание справедливости аксиомы о невозможности полной безопасности вовсе не означает того, что к опасностям следует относиться безразлично, что опасный окружающий мир нужно принимать пассивно как неизменную данность. Здесь следует обратить внимание на два обстоятельства.

Во-первых, существуют опасности, выявление и полное исключение которых все-таки возможно. Их иногда (в контексте традиционной трудоохранной терминологии) называют опасными производственными факторами . Например, лестница без перил

при пользовании ей несет опасность падения с высоты. Она может быть полностью устранена путем сооружения перил. Правда, существуют и другие опасности, создаваемые пользованием лестницей, не устраняемые принятием названной меры.

Во-вторых, существуют опасности, которые, хотя и невозможно полностью устранить, но вполне можно уменьшить степень их вредного воздействия на человека. Например, степень вредного воздействия на глаза электросварщика такой опасности, как яркий свет электросварочной дуги, можно существенно уменьшить путем использования специальных светозащитных стекол очков (обобщенно говоря, путем применения средств индивидуальной защиты работающего).

С последним тезисом, однако, связана серьезная методологическая проблема. Чтобы говорить об уменьшении степени вредного воздействия опасности, необходимо формализовать это понятие, дать ему числовую характеристику. Желательно также, чтобы эта числовая характеристика была универсальной , то есть единым образом характеризовала бы опасности разной природы, позволяла бы сравнивать опасности между собой.

Такой характеристикой может быть риск опасности - произведение вероятности вредного воздействия опасности на наносимый этим воздействием ущерб :

r = pd

Здесь r - риск; p - вероятность вредного воздействия опасности; d - наносимый ущерб (от латинского «damnum» - «ущерб»). Вероятность является безразмерной величиной, поэтому определенный таким образом риск опасности измеряется в тех же единицах, что и ущерб.

Если исследуется индивидуальный риск , то ущерб является безразмерной величиной, значения которой неотрицательны и не превосходят единицы. Нуль ущерба соответствует его отсутствию, единица ущерба означает смерть или гибель индивида. Тогда и риск получается безразмерной величиной, принимающей значения из диапазона [0; 1] . Смысл конкретного значения индивидуального риска легко пояснить следующим примером.

В трудоохранной практике многих стран существует понятие приемлемого риска . Если риск некоторой опасности не превосходит приемлемого (предельно допустимого)

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ риска, то по поводу нее можно не принимать трудоохранных мер. Пусть конкретным значением приемлемого риска будет 10-9. Смысл этого значения таков: опасность с риском 10-9 – это такая опасность, которая (упрощенно говоря), многократно воздействуя на миллиард индивидов, приведет к смерти или гибели в среднем только одного из них. Если в некоторых условиях выявляется опасность, риск которой больше приемлемого, то должны быть приняты меры по снижению риска до уровня не выше приемлемого (меры по управлению этим риском).

Если исследуют коллективные риски , то ущерб оценивают в денежных единицах. Тогда и риск оказывается измеренным в денежных единицах. Например, если риск некоторой опасности равен 2000 рублей, то это упрощенно означает следующее: если вредное воздействие опасности осуществится в полной мере (вероятность принята равной единице), то ущерб, нанесенный коллективу (предприятию, организации обществу), составит ровно 2000 рублей.

Нужно отметить, что точное определение рисков опасностей – трудная (а для многих практических ситуаций невыполнимая) задача. Поэтому вместо вычисления рисков часто говорят об их оценке [5]. Значения рисков опасностей, получаемые оценочными способами, часто удобно измерять в условных единицах. Их выбирают так, чтобы нули условной и абсолютной шкал совпадали. Риск опасности, измеренный в условной шкале, оказывается неотрицательной величиной, но уже необязательно не превосходящей единицу.

Например, если вероятность вредного воздействия опасности оценивать как малую, среднюю и высокую, а ущерб, наносимый вредным воздействием опасности, – как низкий, средний и высокий, то можно построить для оценки рисков опасностей пятибалльную шкалу (от 0 до 4 баллов), представленную в таблице 1.

Для оценки рисков можно использовать и другие способы, например, метод экспертной оценки . Так что, вообще говоря, относительно числового значения риска, полученного оценочными способами, можно быть уверенным лишь в том, что оно неотрицательно, и что его нуль соответствует отсутствию вредного воздействия опасности. Другие свойства этой величины зависят от условий рассмотрения и решения конкретной трудоохранной проблемы (или проблемы обеспечения безопасности жизнедеятельности).

Таблица 1. Пятибалльная шкала оценки рисков опасностей

г	Малая вероятность	Средняя вероятность	Высокая вероятность
Низкий ущерб	0	1	2
Средний ущерб	1	2	3
Высокий ущерб	2	3	4

Вкратце таковы основы теории рисков трудовых опасностей, их оценки и управления ими. Далее внимание исследователей, преподавателей и практиков в основном устремляется к качественному (в противовес количественному) анализу соответствующей нормативной, правовой, организационной, управленческой, методологической, методической и прочих подобных сторон рассматриваемого вопроса. При этом наиболее трудной математической задачей оказывается сравнение двух действительных чисел или вычисление статистических показателей и проверка справедливости выдвигаемых статистических гипотез. Нисколько не умаляя теоретической ценности и практической значимости названной деятельности, отметим, что при этом остается в стороне весьма актуальный содержательно и интересный с математико-прикладной точки зрения аспект, на который мы сейчас предлагаем обратить внимание.

В фокусе нашего зрения находится типовая предметная ситуация, называемая нами стандартной задачей минимизации рисков трудовых опасностей . Она состоит в следующем. Планируется мероприятие (образовательное, производственное, общественное и так далее), связанное с выполнением его участниками комплекса работ L 1, ..., Ln (окраска стульев, мытье окон, рисование стенной газеты и тому подобное). Здесь n - натуральное число, обычно большее единицы. Для обозначения отдельной работы нами выбрана буква L от латинского «labor» - «труд». Выполнение единицы каждой из работ L 1 , .„, L n сопряжено с вредным воздействием на работающих трудовых опасностей, оцениваемым соответственно в c 1 , ..., c_n единиц риска. Будем называть неотрицательные действительные числа C j (j=1..n ) показателями рисковости соответствующих им работ L j . Мы предполагаем, что исследуемый комплекс обладает свойством аддитивности [3, с. 38]: если выполнение х 1 единиц работы L 1 приводит к появлению r 1 единиц риска, а выполнение х₂ единиц работы L 2 приводит к появлению r₂ единиц риска, то выполнение тех же работ в тех же объемах в комплексе приводит

к появлению r 1 + r₂ единиц риска. Отметим, что для многих предметных областей требование аддитивности можно считать выполненным (хотя бы приближенно). Если план предусматривает выполнение работ L 1 , .„, L n в объемах соответственно X 1 , „., x n , то суммарный риск (в предположении справедливости условия аддитивности) будет таким:

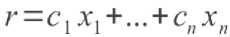
Иначе говоря, суммарный риск является линейной функцией от n аргументов (объемов работ). Коэффициентами в линейной форме, задающей эту целевую функцию, являются показатели рисковости работ. Если сейчас попытаться минимизировать суммарный риск, то мы придем к абсурду с содержательной точки зрения: следует все X j (j=1..n ) положить равными нулю. Тогда суммарный риск тоже обнулится, а это и есть его наименьшее возможное значение. Действительно, по содержательному смыслу задачи объемы работ неотрицательны, неотрицательны и все коэффициенты линейной формы, задающей суммарный риск. Неотрицательно определенной тогда будет и сама линейная форма, а наименьшим значением неотрицательно определенной величины является нуль. Содержательно же такой «план» означает отказ от выполнения работ с целью полного устранения опасностей. Вряд ли найдется здравомыслящий субъект, признававший бы решения подобного рода оптимальными.

Поэтому добавим к условию задачи следующее: в результате выполнения работ должны быть получены измеримые эффекты E 1 , .„, E m ( m - натуральное число, вовсе не обязательно равное n ) в количествах, не меньших чем b 1 , …, b m . Количество единиц эффекта E i , получаемое в результате выполнения единицы работы L j обозначим a ij и будем называть эффективностью работы L j в смысле эффекта E i . Получающуюся при этом матрицу будем называть матрицей эффективностей работ.

Понятно теперь, что допустимым является не любой план, а лишь такой, компоненты которого удовлетворяют системе неравенств:

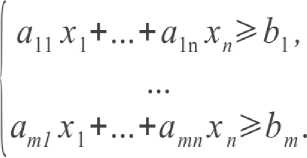
Очевидно, что при положительных нормах Ь 1 , .„, b_m эффектов E 1 , .„, E_m и отличии

хотя бы одного из элементов матрицы эффективностей от нуля (к тому же все они по предметному смыслу задачи неотрицательны) обсуждавшийся нами выше наивный «план» не является допустимым. Таким образом, введение системы ограничений-неравенств гарантирует нам, по меньшей мере, «защищенность» от очевидно бессмысленных решений.

К сказанному следует добавить еще и требование неотрицательности значений всех компонентов плана работ (оно следует непосредственно из предметного смысла рассматриваемой нами задачи):

х^-.х^О

Сама же задача состоит в том, чтобы составить план работ, компоненты которого (объемы работ) были бы неотрицательны, обеспечивали бы выполнение (допускается и перевыполнение) норм требуемых эффектов. Из всех допустимых планов оптимальным признается тот, который приводит к наименьшему из всех возможных (минимальному) суммарному риску трудовых опасностей. Это и есть стандартная задача минимизации рисков трудовых опасностей. Система ее входных данных (параметров) представлена в таблице 2.

Таблица 2. Компактное представление входных данных стандартной задачи минимизации рисков трудовых опасностей

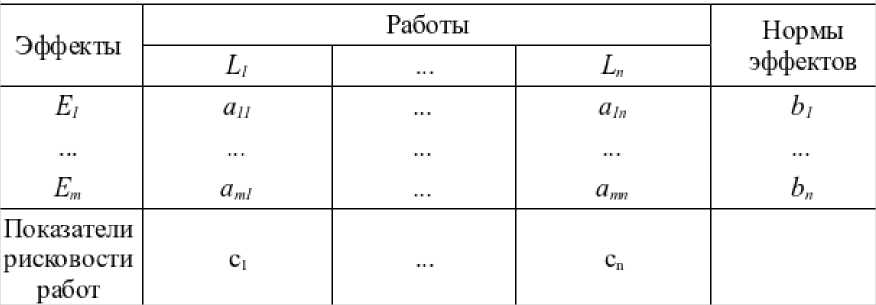
Математической моделью стандартной задачи минимизации рисков трудовых опасностей является требование нахождения n неотрицательных чисел x1, …, xn, обращающих в минимум значение линейной формы и удовлетворяющих системе m неравенств:

г—сх хт + ... + cnxn-^min аиххА..ЛаХпхп>Ьх,

а ,хл ЛЛа x ^b .

ml 1 mn n m

Такие модели в математике называются стандартными задачами линейного программирования на поиск минимума целевой функции . Линейная форма, минимальное значение которой должно быть получено, называется целевой функцией . Раздел математики, в котором изучаются подобные задачи, называется линейным программированием . Термин предложен Дж. Б. Данцигом [3] в 1949 году, он ничего общего не имеет с программированием вычислительных машин: английское слово «programming» имеет в качестве одного из своих значений «планирование», что вполне соответствует предметному смыслу подобных задач. Впервые (как математические модели экономических проблем) задачи линейного программирования предложил изучать Л.В. Канторович [4] в 1939 году. Универсальный метод решения задач линейного программирования (симплексный метод) разработал Дж. Б. Данциг в 1949 году.

Существуют и другие методы решения таких задач. Если количество неизвестных равно двум, то удобен и нагляден графический метод, предложенный еще Л.В. Канторовичем [1, с. 16]. Если число неизвестных больше двух, но количество неравенств-ограничений точно равно двум, то можно применить графический метод, предложенный Дж. Б. Данцигом [3, с. 51]. Если и количество неизвестных, и количество неравенств-ограничений больше двух, то можно применить метод Фурье-Моцкина [3, c. 87] или метод эллипсоидов, предложенный в 1979 году советским математиком Л.Г. Хачияном [2, c. 288]. Поиск эффективных методов решения задач линейного программирования продолжается. В настоящее время наиболее широко при решении практических проблем используется симплексный метод.

Иногда стандартная задача минимизации рисков трудовых опасностей не может быть сведена к стандартной задаче линейного программирования на поиск минимума целевой функции. Связано это с тем, что иногда объемы работ x 1 , …, x n должны удовлетворять кроме системы неравенств-ограничений и требования неотрицательности

еще и требованию целочисленности. Например, если объем работ характеризуется количеством собранных системных блоков персональных компьютеров или количеством решенных обучающимся расчетных задач, то он никак не может быть измерен нецелым числом. В этом случае можно математическую модель называть задачей целочисленного программирования, соответствующей стандартной задаче линейного программирования на поиск минимума целевой функции . Такие задачи изучаются общим разделом математики – математическим программированием (более узко – дискретным программированием , еще более узко – целочисленным программированием ). Если стандартная задача минимизации рисков трудовых опасностей приводит к задаче целочисленного программирования, то для ее решения можно применить, например, метод Гомори, основанный на симплексном методе [1, c. 180].

Итак, стандартная задача линейного программирования на поиск минимума целевой функции или соответствующая ей задача целочисленного программирования (формальная система) является математической моделью стандартной задачи минимизации рисков трудовых опасностей (содержательной системы). Обращая это суждение, можно сказать: стандартная задача минимизации рисков трудовых опасностей является интерпретацией стандартной задачи линейного программирования на поиск минимума целевой функции или соответствующей ей задачи целочисленного программирования. Тем самым полностью оправданы почти все элементы формулировки названия этой статьи. Мы говорим «почти», потому что одно пока остается не вполне ясным: почему построенная нами интерпретация названа «образовательнотрудоохранной», а не просто «трудоохранной» – независимо от того, труд какой именно хозяйственной отрасли подлежит охране. К объяснению этого нюанса мы теперь приступаем.

Наша интерпретация является трудоохранной в любом случае и может иметь значимость даже безо всякой связи с образованием. Хотя, конечно, важен уже и тот факт, что предметное ее содержание является ценным дополнением, к содержанию образования названных в начале статьи категорий обучающихся. Но еще более важно другое: в производственной сфере иногда (и, к счастью, не всегда) сами объемы работ выступают в качестве требуемых эффектов. Иначе говоря, довольно часто (особенно когда речь идет не о предприятии в целом, а лишь о его подразделении, производственном участке) основным требуемым эффектом как раз и является точное выполнение полученного плана

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ как по ассортименту продукции, так и по объемам работ. В этом случае предмет нашей стандартной задачи минимизации рисков трудовых опасностей исчезает (оптимизирующее планирование невозможно, так как план уже задан), хотя объект и остается актуальным (снижение рисков трудовых опасностей является возможным, но уже способами, не охватываемыми нашей стандартной задачей). Таким образом, стандартная задача минимизации рисков трудовых опасностей не всегда является адекватной моделью реальных производственных проблем и процессов.

В образовании же ситуация является совершенно иной. Здесь выполняемые работы (трудовые действия) сами по себе никогда не являются требуемыми эффектами (целями образования или результатами решения частных образовательных задач). Поэтому, насколько странным и удивительным это утверждение не показалось бы сначала, предложенная нами содержательная интерпретация даже более актуальна для образования, чем для производств, непосредственно с ним не связанных.

Придя к этому важному общему выводу, приведем теперь конкретный пример постановки и решения стандартной задачи минимизации рисков трудовых опасностей образовательно-трудоохранного содержания. Предупредим, что сообщаемые нами числовые данные являются гипотетическими и взяты с чисто методической (иллюстративной) целью.

Мастер производственного обучения образовательного учреждения среднего профессионального образования, ведущего подготовку квалифицированных рабочих строительного профиля, планирует вместе с группой студентов принять участие в добровольном воспитательно-трудовом мероприятии, в ходе которого предполагается выполнить отделку части забора, огораживающего территорию учреждения. Отделка может выполняться вручную или с применением средств малой механизации труда. В мероприятии следует задействовать не менее 15 студентов и обеспечить им трудовую занятость не менее чем на 2 часа (иными словами, общие трудозатраты должны составить не менее 30 человеко-часов).

Отделка одной секции забора вручную должна выполняться малой группой студентов в количестве 3 человек, трудозатраты составляют 10 человеко-часов. Тот же объем работ, выполняемый с применением средств малой механизации, требует участия 2 человек, трудозатраты равны 3 человеко-часа. Согласно данным экспертной оценки, отделка одной секции сопровождается 2-мя условными единицами риска трудовых опасностей при механизированном способе и 4-мя единицами риска при ручном способе

выполнения работ.

Необходимо составить план работ (указать количество секций, которое предполагается отделать каждым из названных двух способов), обеспечивающий наименьший возможный суммарный риск трудовых опасностей.

Представив данные задачи в компактной форме, приходим к выводу, что поставленная задача является стандартной задачей минимизации рисков трудовых опасностей (таблица 3):

Таблица 3. Компактное представление данных рассматриваемого примера

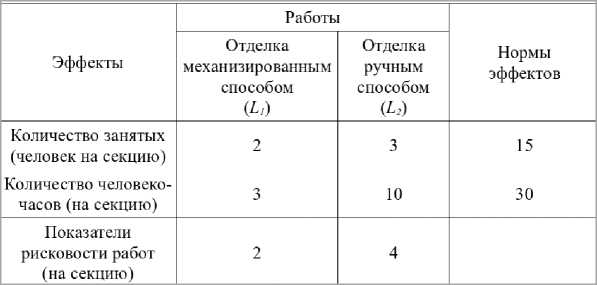
Обозначив буквами x 1 и x 2 количества секций забора, которые планируется отделать соответственно механизированным и ручным способом, по данным таблицы 3 (аналогично общему случаю, представленному ранее в таблице 2) строим математическую модель – задачу целочисленного программирования, соответствующую стандартной задаче линейного программирования на поиск минимума целевой функции (ведь количества x 1 и x 2 должны быть целыми):

r —2x_x+4x₂”>min 2x₁+3x₂^15, 3x, + 10x₂^30.

X], х2>0

Ее решение графическим методом представлено на рисунке 1. Прямая AB , проходящая через точки (0; 5) и (7,5; 0) изображает множество точек, координаты которых ( x 1 ; x 2 ) удовлетворяют равенству 2x 1 + 3x 2 = 15 . Эта прямая делит координатную плоскость на две полуплоскости. Неравенству 2x 1 + 3x 2 ⩾ 15 удовлетворяют координаты

точек, лежащих на вышеназванной прямой или «выше» нее (то есть в той полуплоскости, которой не принадлежит начало отсчета). Аналогично, координаты точек, лежащих на проходящей через точки (0; 3) и (10; 0) прямой CD или «выше» нее, удовлетворяют неравенству 3x 1 + 10x 2 ⩾ 30 . В области допустимых значений отмечены точки с целочисленными координатами. Проходящая через точки (0; 2) и (4; 0) прямая - это линия уровня целевой функции, соответствующая значению r = 8 . Если ее смещать параллельно себе самой «вверх», то будут получаться новые линии уровня, соответствующие большим значениям целевой функции. Поскольку нас интересует наименьшее ее значение, но достигаемое в целочисленной точке допустимой области, то описанное выше смещение следует прекратить, как только линия уровня «впервые» пройдет через отмеченную точку.

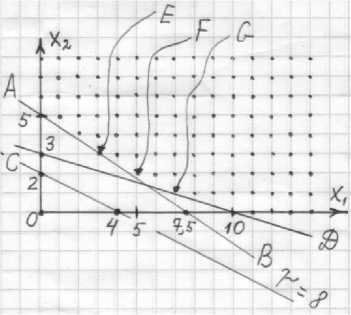
Рис. 1. Иллюстрация решения графическим методом математической задачи, к которой сводится стандартная задача минимизации рисков трудовых опасностей с данными из таблицы 3

Нетрудно видеть, что рассматриваемая нами задача имеет не одно, а даже три решения, в равной мере удовлетворяющие критерию оптимальности: они соответствуют точкам E(3; 3), F(5; 2) и G(7; 1) , лежащим на линии уровня r = 18 . Всем остальным точкам с целочисленными неотрицательными координатами, лежащим в допустимой области, отвечают более высокие значения целевой функции.

Содержательная интерпретация полученного решения такова. Во-первых, можно запланировать отделать три секции забора механизированным способом и три вручную (решение E ). В этих работах будут заняты 15 студентов, трудозатраты составят 39 человеко-часов (то есть выполнение работ займет 39 /15 = 2,6 часа или 2 часа 36 минут). Суммарный риск трудовых опасностей составит 18 единиц. Во-вторых, можно запланировать отделать пять секций забора механизированным способом и две вручную

(решение F ). Заняты будут 16 человек, трудозатраты составят 35 человеко-часов (выполнение работ займет 35 / 16 ≈ 2,2 часа или 2 часа 12 минут). Суммарный риск составит 18 единиц. В-третьих, можно запланировать отделать семь секций забора механизированным способом и одну вручную (решение G ). Заняты будут 17 студентов, трудозатраты равны 31 человеко-час (то есть выполнение работ завершится через 31 / 17 ≈ 1,8 часа или 1 час 48 минут). Суммарный риск будет таким же, как и в предыдущих двух случаях. Третье решение, строго говоря, не удовлетворяет изначальному требованию, состоящему в том, что время выполнения работ должно быть не менее двух часов. Поэтому третье решение может быть (а строго говоря – должно быть) отброшено. А из первых двух педагог может выбирать, привлекая, быть может, и другие критерии, кроме вошедших в исследованную нами модель.

На этом мы завершаем рассмотрение конкретного практического примера и переходим к подведению итогов нашего исследования.

• 1.    Нами предложена содержательная модель , охватывающая множество реальных трудоохранных ситуаций- стандартная задача минимизации рисков трудовых опасностей . Будучи применимой в различных сферах трудовой деятельности человека, она, по нашему мнению, является особенно актуальной там, где полезным эффектом труда является не само по себе выполнение плана работ, а требуется достижение целей (решение задач), выходящих за рамки собственно производственных. Прежде всего, это касается образования. Именно поэтому мы характеризуем предложенную нами содержательную модель как образовательно -трудоохранную.

• 2.    Предложенная нами содержательная модель оказалась интерпретацией стандартной задачи линейного программирования на поиск минимума целевой функции или соответствующей ей задачи целочисленного программирования. Мы полагаем, что как в области собственно охраны труда (и вообще безопасности жизнедеятельности), так и в области преподавания названных предметов, найденная нами интерпретация не является единственно возможной. Мы думаем, что исследования в инициированном нами направлении следует продолжать с целью получения новых содержательных (предметных) интерпретаций и результатов.