Обсчет пиков в задачах электрофореза

Информационные сигналы, полученные с детекторов прибора, как правило, подлежат первичной и вторичной обработке. Первичная обработка — выделение сигнала из шума [1]. Вторичная обработка — определение параметров сигналов [1]. В статье описаны методы вторичной обработки применительно для задач электрофореза ДНК. После первичной обработки сигнал представляет собой набор пиков, отличающихся друг от друга в основном временем выхода. Для определения местоположения пиков применяются методы поиска экстремальных точек — максимумов. Для их поиска применяются различные методы, описанные в литературе. Один из методов предложен в статье [2].

После того как положение максимумов, а значит, и примерное положение пиков известно, необходимо определить их параметры. В качестве модели пика была выбрана гауссова кривая, т. е. f ( t ) = x 1 • e^{x 2}( t - ^{x з )} . Ее параметрами являются амплитуда ( x 1 ), ширина _п =__ L и положение ( x ₃ ).

\ 2 x ₂

В статье [2] был предложен метод для определения амплитуды, ширины и положения пиков с помощью квазиньютоновских методов. Здесь будет приведен результат работы данного метода.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПИКА

Метод, описанный в [2], состоит в следующем. Если f ( t ) = x 1 • e x ²( t - ^{x з )} и имеется набор измерений f i , то задача сводится к поиску

m min F(xi,x2,xз) = ^(f — xi • ex2(t -x3? )2 •      (1)

^x 1 . ^x 2 . ^x 3                                 i = 1

Эта задача носит название нелинейной задачи наименьших квадратов [3]. Задача оптимизации состоит в минимизации F(x). Алгоритмы для минимизации функции п переменных разрабатываются уже свыше 140 лет. Наиболее распространенными являются метод наискорейшего спуска и многомерный метод Ньютона. Достоинство метода наискорейшего спуска заключается в том, что он всегда сходится, если функция F(x) имеет непрерывные производные. Но в некоторых случаях он сходится довольно медленно (иногда требуется более ста итераций).

Этого можно избежать, применяя п- мерный аналог метода Ньютона. Функция F записывается в виде

F ( x ) =

= F ( x ) + p^T V F ( x ) + 2 p^T V ² F ( x ) p =

= F ( x ) + Q ( p ). ⁽²⁾

Чтобы получить шаг p , минимизируется квадратичная функция Q ( p ) при помощи построения ее градиента по р. В конечном итоге получается:

x k+ 1 = x k + р = x k - V ² F ( x k ) ^- 1 V F ( x k ). (3)

Метод Ньютона в n- мерном случае обладает свойством быстрой сходимости, а именно он сходится квадратично в окрестности решения

Ixk+1 - x 1L * в Ixk - x t ’ (4)

где в — некоторая неотрицательная константа, зависящая от F ( x ) .

Но у метода Ньютона также есть недостатки. Например, он может не сходиться. Но если матрица V ² F ^{- г} положительно определена, т. е. удовлетворяет условию z ^T V ² F ^{- 1} z >  0 для всех z * 0, то в этом случае направление метода Ньютона гарантировано будет направлением спуска [3].

Еще одним недостатком метода Ньютона является необходимость вычислять матрицу вторых производных [3].

Для того чтобы получить альтернативные эффективные и практичные методы, можно аппроксимировать гессиан в ходе минимизации функции. Эти методы основаны на аппроксимации гессиана секущими и являются обобщением метода секущих. Если B_k = V ² F k = F ( x ), то шаг на k -й итерации будет определяться из системы

B k p = - V F k . (5)

Таким образом, мы получаем вариант метода Ньютона, в котором используется приближенный гессиан. Новая аппроксимация гессиана выбирается так, чтобы

^Bk+ 1 ⁽ x k+ 1 ^- x k ) = ^V F k+ 1 ^{- V} F k . ⁽⁶⁾

В одномерном случае это однозначно определяет B_k+ 1 . При более высоких размерностях для того, чтобы определить B k+ 1 , необходимы дополнительные условия.

Поскольку нам необходимо на каждой итерации вычислять обратную матрицу B ^-1, можно еще упростить метод Ньютона, используя алгоритм Шермана—Моррисона для приближенного вычисления обратной матрицы. Предположим, что для матрицы B_k вычислена обратная B_k ¹ . Пусть на следующей итерации матрица

B k+ 1 = B k — uv ^T, (7)

где u и v — векторы размерности n . Тогда матрицу B k _{+ 1} можно вычислять по формуле

Bk+ 1 = B - + а ( B;¹ u )( v ^T B ;¹), ⁽⁸⁾

где а = 1/(1 - v ^T B k -¹ u ). На это будет затрачено O ( n ²) арифметических операций по сравнению с O ( n ³) операций при стандартном вычислении новой обратной матрицы.

Для упрощения выбора векторов u и v полагаем, что u i = v i . Это обосновано, поскольку матрица вторых производных является симметричной. Для получения более достоверного результата элемент { B 11 } _k вычислялся как d² F /d x ².

Важно, что достаточно хорошо нужно подобрать центр пика. Для этого применялся метод поиска центра масс. Для уточнения полученного результата использовался метод наименьших квадратов отдельно для параметра x ₃. И только после этого можно применять описанный выше метод.

Провести оценку метода можно по стандартному отклонению, стандартным ошибкам, доверительным интервалам или по величине R -квадрат. Но большинство этих оценок предназначено для оценки состоятельности модели и применимости метода наименьших квадратов. Чтобы оценить работу самого метода, здесь использовался график шкалированных невязок, т. е. невязок, деленных

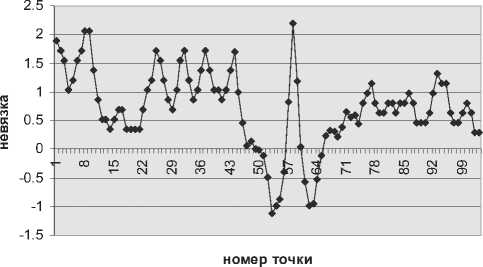
Рис. 1. График шкалированных невязок для пред ложенного метода

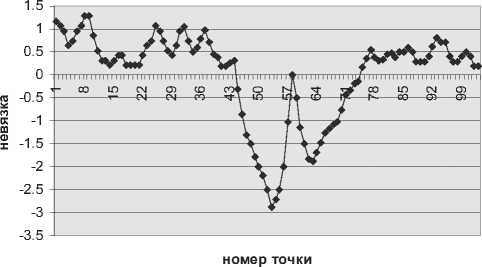
Рис. 2. График шкалированных невязок для метода сравнения на стандартное отклонение. Примерно 95 % шкалированных невязок должно лежать в интервале [-2, 2] [3].

График невязок, показанный на рис. 1, был взят для случайного пика. Пик аппроксимировался по 103 точкам. Из них 3 значения не попали в интервал [-2, 2], что составляет примерно 3 %.

Для сравнения результатов параметры данного пика были вычислены другим, более простым методом. В этом методе: амплитуда пика — это его максимальное значение; полуширина — вычислена по его площади ( S = л)2па Н ); положение — вычислено методом наименьших квадратов. На рис. 2 приведен график шкалированных невязок для этих вычислений. Из графика видно, что 6 точек не лежат в интервале [ - 2, 2], что составляет примерно 6 % и, следовательно, является неудовлетворительным результатом.

Предложенный метод достаточно прост в реализации и не требует большого объема вычислений. В результате использования данного метода получены результаты, подтверждающие необходимость его использования.

ЗАКЛЮЧЕНИЕ

В статье приведены результаты испытания метода для обсчета пиков в электрофорезе ДНК. Метод позволяет достаточно быстро определить параметры пиков. График невязок показал, что метод достаточно хорошо работает для таких задач. Однако большинство невязок лежит в положительной области, что говорит о неидеальности метода и выбранной модели для описания пиков.