Обтекание треугольного крыла с малым углом стреловидности передней кромки на режиме сильного взаимодействия

Характер течения в трехмерном ламинарном пограничном слое на. треугольном крыле, обтекаемом гиперзвуковым потоком вязкого газа, зависит от многих определяющих параметров. Гиперзвуковое обтекание треугольной пластины на. режиме сильного взаимодействия пограничного слоя с внешним потоком впервые рассмотрено в [1, 2], где было показано, что решение задачи зависит только от двух независимых переменных, однако полученное автомодельное (по продольной координате) решение не удовлетворяет условию непротекания в плоскости симметрии крыла. Исследование течения на. нехолодных треугольных крыльях показало, что на. режиме сильного вязкого взаимодействия разложение решения в окрестности передней кромки не единственно, а. содержит произвольную константу [3]. При соответствующем подборе ее, в принципе, можно удовлетворить условиям вниз по потоку (в плоскости симметрии). В [4] были получены глобальные решения уравнений ламинарного пограничного слоя на. треугольном крыле с размахом порядка, единицы, при этом система, уравнений в частных производных решалась конечно-разностным методом [5]. Результаты исследования влияния различных параметров на. характеристики течений около треугольных крыльев приведены в [6, 7]. В [8] изучены некоторые особенности обтекания нехолодной треугольной пластины с размахом порядка единицы на режиме вязко-невязкого взаимодействия. Была, отмечена, возможность существования в окрестности плоскости симметрии течения, которое описывается уравнениями взаимодействующего пограничного слоя. Для главных членов разложения функций течения в окрестности плоскости симметрии была, сформулирована, краевая задача. Полученная система, обыкновенных дифференциальных уравнений содержит параметр, который определяет допустимые виды решений и зависит от сращивания этого решения с решением, которое строится от передней кромки [3]. В [9, 10] было показано, что значение этого параметра, наиболее сильно влияет на. профиль производной от поперечной компоненты скорости по размаху крыла, и было установлено, что уравнение поперечного импульса, в общем случае не может быть решено методом прогонки, так как из-за. наличия неоднородного члена, нарушается достаточный признак хорошей обусловленности [11]. Для решения этого дифференциального уравнения краевая задача редуцировалась к задаче Коши, для решения которой использовалась схема Рунге-Кутты. В общем случае если сращивание решений будет происходить при конечных значениях поперечной координаты, то необходимо принимать в учет следующие члены разложений в окрестности плоскости симметрии. Для определения последующих членов разложения получаются краевые задачи, но уже с нулевыми краевыми условиями. Решение каждой последующей краевой задачи позволяет, в принципе, вычислить «произвольный параметр» для решения предыдущей краевой задачи, но очевидно, что само ее решение зависит от нового произвольного параметра для следующего члена разложения в окрестности плоскости симметрии. Сращивание решений, в принципе, позволяет определить значения константы в разложении от передней кромки, параметра в разложении в окрестности плоскости симметрии и координату, где происходит сращивание, если, конечно, течение в окрестности плоскости симметрии крыла с размахом порядка единицы описывается уравнениями пограничного слоя.

В настоящей работе исследуется обтекание полубесконечной треугольной пластины с малым углом стреловидности на режиме сильного взаимодействия. Как будет показано ниже, в этом случае поперечная компонента скорости в пограничном слое мала и область локальной неприменимости уравнений пограничного слоя в окрестности плоскости симметрии крыла не возникает [8]. В результате в окрестности плоскости симметрии крыла разложение для функций течения вместо координатного становится координатно-параметрическим и появляется возможность последовательно определять вид разложений для функций течения с заданной точностью. Построение решения в окрестности передней кромки позволило определить собственные числа, величина которых определяет передачу возмущений вверх по потоку. Сращивание этого решения с решением в окрестности плоскости симметрии позволило найти значение константы в разложении около передней кромки и значение поперечной координаты, при которой происходит сращивание двух решений. Сравнение полученного разложения для индуцированного давления с решением краевой задачи в частных производных позволило определить область применимости данного подхода.

2.    Постановка задачи

Рассматривается симметричное обтекание полубесконечной треугольной пластины на режиме сильного взаимодействия при температуре поверхности T_w. Газ считается совершенным с отношением удельных теплоемкостей у = c_p / c_v и коэффициентом вязкости, линейно зависящем от температуры: д°/д_го = С ^Т ° / Т ^, г де С ^ = const, а ин деке то обозначает параметры в невозмущенном потоке. Компоненты вектора скорости u°, v°, w° в пограничном слое направлены вдоль осей ж°, у°, z° системы координат, начало которой расположено в вершине крыла. Ось ж° направлена вдоль оси симметрии крыла, а ось z° — по размаху крыла. Предполагается, что угол стреловидности передней кромки 3 <<  1, а размах крыла s = ctg3 >>  1- Вводится ма.тый параметр е = s²<<  1. В певозмущеи-ном потоке п^ — скорость, р^ — плотность и д^ — энтальпия торможения стремятся к постоянным значениям, когда число Маха М^ ^ то, тогда р^ — давление, а^ — скорость звука и Т^ — температура стремятся к нулю.

В соответствии с гиперзвуковой теорией малых возмущений [12] при М^ >>  1 и безразмерной толщине пограничного слоя 6 <<  1, в случае когда М^б >>  1, индуцированное давление имеет порядок р ° ~ р^п^б². Так как в пограничном слое статическая энтальпия h ° ~ п^/2, то, используя уравнение состояния, для оценки плотности газа в пограничном слое получаем

Р° ^ P°h^ ^ P^ujS²   ^   ^ 62

рх   Р^һ °      р _х   (у - 1) uj

Оценка для толщины 6 получается после приравнивания главных вязких и инерционных членов в уравнении переноса количества движения вдоль оси ж°:

о о ^ди°     ^д ( о ^ди°\ p » ⁵"^ »    Р ° ^и»       -1/4

■ ■  ~ к°Рд^) ’^Т» ~     ’⁵ ~Re •

Здесь Re о = p » u » L / ро — число Вейнольдса, ро — коэффициент вязкости, вычисленный при температуре торможения То, L — характерный размер, который при рассмотрении обтекания полубесконечного крыла, в силу автомодельности, в конечные результаты не входит. Для оценки величины поперечного компонента скорости w° необходимо учесть, что он создается в пространственном пограничном слое градиентом давления по размаху крыла. Приравнивая главные инерционные члены и градиент давления в уравнении переноса количества движения вдоль оси z°, получаем

° ° дw° ^ др° p » 5²u » w ° ^ p » u » 5² w° ^ ,-

^{Р П} дХ° дz ° ’ L           sL ’ и» ^Е"

Заметим, что вне пограничного слоя, где плотность газа велика, этот компонент скорости существенно меньше, т.к. имеет порядок w ° /u » ~ 5²/ s = 52Д- << 1 [13]. Следовательно, в пограничном слое на крыле с малым углом стреловидности возникают поперечные течения со скоростью порядка Д-и», тогда как на крыле с размахом порядка единицы поперечная компонента скорости существенно больше w °/ u » = О (1) [14]. Оценка для компоненты скорости нормальной к поверхности крыла имеет обычный порядок v° ~ и» 5.

В предположении, что М»5 >>  1, для определения индуцированного давления, создаваемого толщиной вытеснения, можно использовать формулу «касательного клина» [12]. В соответствии с оценками для ламинарного пограничного слоя в гиперзвуковом потоке [12], оценками (1) - (3) и учитывая преобразование А. А. Дородницына, вводятся безразмерные переменные:

х ° = Lx

V° = L5 Р Р^ = l-^V2 ;

0 Р

Р ° = p » u » 5²p ( Х’ z ) ’ p = p»52p ( Х’ А’ z) ’ р° = рор (Х’ А’ z) ’

до = 0.5и»д (Х’ А’ z) ’ и° = и» и (Х’ А’ z) ’ w° = и» Д-w (Х’ А’ z) ’ v° = и»5 p 1

^v ( Х’ А’ z )

дА дАА идХ — ^әр)

’ 5° = L55_e ’ 5 = Яе_о ^1/4 •

Здесь д° - энтальпия торможения, 5° - размерная толщина пограничного слоя. В переменных (4) для полубесконечного треугольного крыла большого размаха система уравнений пространственного пограничного слоя сводится к виду:

ди  дv   дw

+   +     = 0’ дХ дА   дz ди _ди     ди    1 др   д Р_ ди\ идХ +vдА + -wд"p = - p дХ + дА Х^вА ) '

дw _дw     дw    1 др   д Р _ дw\

.  + 8дА +  ' д = -pдР + дА     Р дд _дд дд   д f_ fl дд 1 -ад (и2 + -w2) \ \

^и дХ ^{+ v} дА ^{+ -w} д i = дА ^^ (а дА " —-- дА--- ) ) ’

2^ р д =       + и2 + -w2’ р = д - и2 — -w2’ р — 1p р =

7 + 1

( ⁸⁵ е )².

—

e

/■

27Р Jo

-

∞

(д — и² — -w²) РА’

А = 0 : и = w = v = 0’ д = д_ш;

А ^ то : и ^ 1’ w ^ 0’ д ^ 1.

Далее рассматривается случай обтекания крыла при g_w = 1 и числе Прандтля ст = 1, тогда уравнение для энтальпии в (5) имеет решение g (ж, A, z) = 1. Заметим, что если в краевой задаче (5) совершить предельный переход e ^ 0 (s ^ то), то для главных членов получаем систему уравнений, которая уже не зависит от компоненты скорости w, и, следовательно, уравнение импульса для w может быть решено после решения системы для главных членов. Как будет установлено ниже, при построении координатно-параметрического разложения в окрестности плоскости симметрии крыла такая ситуация будет иметь место для всех краевых задач для определения следующих коэффициентов членов разложения. Аналогичный вид разложения был получен в [15], где в качестве малого параметра использовалась величина e = у — 1 << 1. Заметим, что при параметре e = 0 (крыло с нулевым углом стреловидности) из (4) следует, что размерная величина поперечной компоненты скорости w^o = 0.

Для учета особенностей поведения функций течения в окрестности вершины треугольного крыла вводится преобразование переменных [6]:

В переменных (6) краевая задача (5) сводится к двумерной, зависящей от координат A* и z, т.к. продольная координата ж выпадает из краевой задачи. Для учета симметричности течения на крыле и поведения функций течения в окрестности передних кромок ( z = ±1) вводятся переменные, подобные [6], которые, однако, не являются автомодельными (по оси z):

A*

У* =                 =

V 5-1 (1 — z2)/2

3,.

, р (z) = V 1 — z² р*,   A (z) = (1 — z²) ⁴ 5*,

^{1 v} * ⁽ у,^ = -

-

z2

р

( ew — uz ) ^+ + дz

V*

V т-1 (1 —     ■'.

z = жz, A = ж1/4А* ,	р = ж 1/2р*(z), р = ж 1/2p* ( A,z ) ,
5 е = ж3/4 5*,	-    -3/4 f*      дА* А                          (6) V = ж /'   V — жи      . дж /

Система уравнений пространственного пограничного слоя и граничные условия на полу-бесконечном плоском треугольном крыле большого размаха (5) с учетом (6), (7) принимают вид:

ди

ди

Г'УГ + v*^— = дz     ду*

у

-

дw

дw

»V + V*^— дz     ду*

дv*

ду*

-

Г =

² УР

( ew

-

-

у

-

A=

/    - / ~ (1

V 2 у р J 0  ^k

-

и2

(ew — uz) (1

-

и'

-

-

2 ур

-

ew2) (

и2

-

z²⁾ р 1,

1 + z2

ew2) fz

+

+

z

-

-

z² dp

Р

dz

z2 dp

Р

dz

uz ) ~ + (y

7 2р     4

ди

дw

-

^z дz ^{+ e} дz

)

-

z ^{1 2}

Р

-

ew²) dу*, р

у +1

А    д ²u

7     ду²’

А    д ²w

) + ду2 ’

[4 (1 + z2) A

= 0,

-

^z (1

-

z2

) ~12

7 dz ,

у* = 0 : u = w = v = 0;   у* ^ то : и ^ 1, w ^ 0.

Решение краевой задачи (8), определяющее течение в пограничном слое на всем крыле, зависит в общем случае от параметров у и e. Система уравнений (8) на передних кромках при z = ±1 вырождается в системы обыкновенных дифференциальных уравнений. Следует отметить, что в уравнения импульсов системы (8) фактически входит вторая производная от толщины вытеснения д2A/дz2. Наличие в системе этой второй производной может приводить к возможности распространения возмущений по размаху крыла [7]. Переходя в краевой задаче (8) к пределу e ^ 0, получается система уравнений, которую можно рассматривать как систему для определения главных членов разложения функций течения в ряды по параметру e. Полученная система разделяется, т.к. в ней функции и, r,p и А зависят только от параметра у и не зависят от компоненты скорости w, и этим она существенно отличается от общего случая (8). Следует отметить, что при значении параметра е = 0 уравнение для компоненты скорости w является линейным дифференциальным уравнением с нулевыми граничными условиями, и его решение определяется после нахождения указанных выше функций течения. Учитывая, что коэффициент при производной по поперечной координате в уравнениях переноса г (г*,z) = —и (г*) zp-1 в этом случае пропорционален z (в главном порядке) и меняет знак то.тько в плоскости симметрии крыла (z = 0). то, следовательно, реализуется течение с плавным стеканием к данной плоскости и на каждой половине крыла направление параболичности системы сохраняется. Так как градиент давления в плоскости симметрии равен нулю в силу предполагаемой симметричности течения, то для компоненты скорости w в плоскости симметрии получается обыкновенное дифференциальное уравнение, которое имеет решение: w (г*,z = 0) = 0 [16]. Аналогичные результаты получены в [17] при рассмотрении течения в ламинарном пограничном слое на конусе при малых углах атаки в сверхзвуковом потоке.

3.    Разложения в окрестности плоскости симметрии крыла и результаты расчетов

Для исследования поведения функций течения в пограничном слое в окрестности плоскости симметрии полубесконечного плоского треугольного крыла оказалось удобным преобразовать краевую задачу (8) и ввести новые переменные:

г = г*p 1/2

г = r*p^1/2 — - (ew — zu) (1 — z²) ^г^. 2                   ' p dz

При таком преобразовании в уравнениях переноса и неразрывности в системе (8) давление в знаменателе останется только при производной от индуцированного давления. После подстановки (9) в краевую задачу (8) она приводится к виду:

г = (ew — uz) (1 — z2) , ди ди г^т + 'А = dz дг дw dw г^т +'А dz дг

У ^{— 1} 2 у

-

У

дг дг

— (ew — uz) 2 +

(1 — u2 — ewV     + z     dP 1

^v           A 2         p dz)

—1

2?

и

-

-

и

-

ew2

) (z

+

— z² dp p dz

)

+

д2и дг2’ д2w дг2 ’

ди

дw

zдz + eдz

+ (ew

-

ги)! dP) ⁽1 — ‘А ’ 2pdz

= 0 ,

(Ю)

А = A 1       ~ ⁽1

V 2 ?p 0_o

— и2 — ew2) d^

p=^ [ 4(1+z2) А—z (1—z2) dA Г • г = 0 : и = w = г = 0; г ^^ : и ^ 1,w ^ 0.

Для исследования поведения функций течения в пространственном пограничном слое в окрестности плоскости симметрии полубесконечного плоского треугольного крыла предполагается, что уравнения пограничного слоя справедливы в этой области и имеют место следующие разложения по малому параметру e и поперечной координате z для функций течения в (10):

/ = /оо ⁽л) + /01 ⁽ л ) ^{е + /}02 ⁽ л) s² + (/10 ⁽л) + /_п⁽ л) ^е) г²+

+/20 (л) г⁴ + О (е³, е² г², ег⁴, г⁶) ,

(И)

w = (шоо (л) + W01 (л) е) г + ww (л) г3 + О (е2г, ег3, г5) , к = коо + ^оіе + ко2е2 + (^10 + кц е) г2 + ^20 г4 + О (е3, е2г2, ег4, г6) , где / = (u, v), а к = (р, Д).

Подставляя разложения (11) в систему уравнений и краевые условия (10) и собирая члены одного порядка по степеням е и/или г, получаем соответствующие краевые задачи. Учитывая, что в систему (10) входят члены р-1, то для обеспечения сходимости ряда к заданной функции необходимо, чтобы выполнялось условие

Роо

(ро1 е + Р10г2 + Р02е2 + ри ег2 + Р20г4 + О (е3, е2г2, ег4, г6))

< 1.

Как следует из (12), при увеличении параметра е область сходимости по координате г уменьшается. В настоящей работе разложения проводились с использованием системы Maple, например, [18].

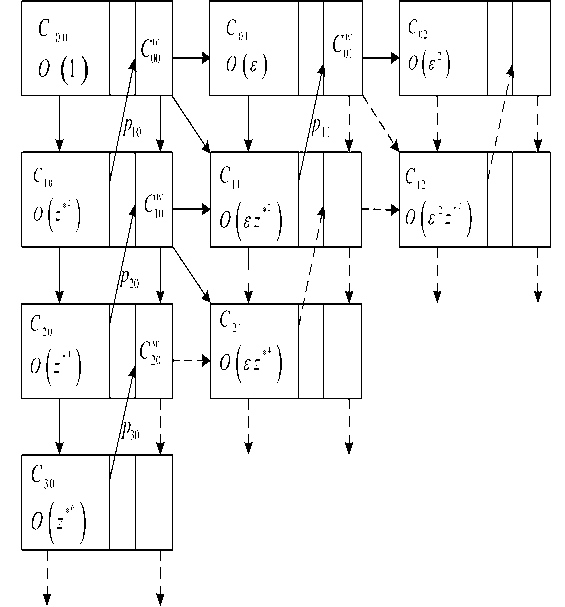
Рис. 1. Условная схема краевых задач и процедура их замыкания

На рис. 1 приведены условные обозначения получающихся краевых задач и процедура их замыкания, которая более подробно будет описана ниже при обсуждении последовательности решения краевых задач. Краевые задачи для вычисления коэффициентов щд (л), v_i g (л), р ід и Д^ обозначаются Сд^ а краевые задачи для вычисления коэффициентов разложения w_i g (л) — С^. Для всех систем, кроме системы Соо ~ 1, краевые условия являются нулевыми. Все системы обыкновенных дифференциальных уравнений решались методом Рунге-Кутты четвертого порядка, для этого краевые задачи редуцировались к задачам Коши. Размер шага по нормальной координате был выбран Дл = 0.01. Были проведены также проверочные расчеты с шагом в два раза меньше — Дл = 0.005, которые показали, что шаг Дл = 0.01 достаточен для обеспечения необходимой точности вычислений.

Краевая задача С_сс ~ (1) и ее решение:

« duoo _ 7 - 1 ,1 _- «2 х + d² «ос С« ос + «со _ 0 dr 47         ^ос,     dr ² ’ dr 4      ’

3 I (7 + 1) (7 — 1) [” _h    2 ^х , л 4 ДрОО~

Рсс _ «у-----7------к  (1- “ос)dr’Асс _ 3V 7+1 ’ r _ 0 : «со _ «со _ 0; r ' х : «со ^ 1.

Как уже отмечалось выше, уравнение для вычисления функции «со (r) отделяется, но его решение зависит от значения коэффициента разложения ріс для давления из системы Сю ~ (^2), которое пока неизвестно. В результате получается краевая задача для определения главного члена для производной от поперечной компоненты скорости СОО ~ (^)

«со^Со - «ос «со _ -^ 11 + 2 ^Р1С 1 ⁽1 - “2₀) + ^ dr                 27         р₀о                dr²

r _ 0 : «со _ 0; r ^ ^ : «ОО ^ 0.

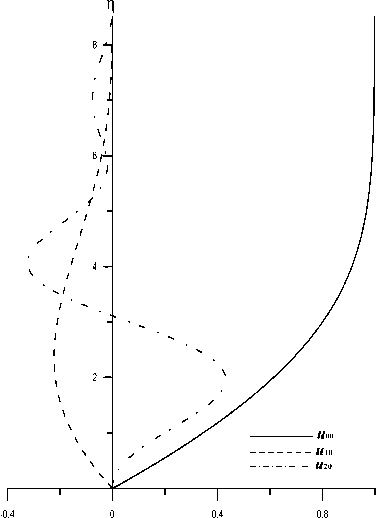
Рис. 2. Коэффициенты разложения в окрестности плоскости симметрии для продольной компоненты скорости «00 (r), «10 (r) и «20 (r)

Далее все результаты расчетов приведены для случая 7 _ 1.4. На рис. 2 приведен профиль продольной компоненты скорости — «со (r)• При решении нелинейной системы (13) методом Рунге-Кутты на поверхности крыла задавалась величина d«ос/dr|^=с _ 0.38109, и в результате получены следующие значения коэффициентов разложения: рос _ 0.81786 и А ос _ 1.10074. Из кривой «со (r )> приведенной на рис. 2, видно, что при заданных определяющих параметрах течения за верхнюю границу пограничного слоя можно брать координату r ~ 8.5. После нахождения функций «_оо (ц ), «_оо (ц ), р_оо и А_оо из системы С_оо ^ (1) можно переходить к решению системы С1о ^ (^2).

Краевая задача С1О ^ (^2) и ее решение:

d-10   7         /1  рщ\

W " 4-10 + "00 (.4 — Р07 = °'

.-00+ -10-    - 2-„о-io =  7 (-2-„0-10 + ( 1 + 4^) ⁽1 - ■    + ^

dp       dp               47                      Р00            )    dp²

,10 = -3 L + ⁵ J < ^{7 + 1)Һ} — ¹¹ [ ~ ^W,) ' Д10 = ² J^ (2 - РЮ7

8 у 7        0                       5 V 7 +1 Р00 / p = ° : -10 = vi0 = °; p ^ то : -10 ^ °.

Система уравнений (15) является линейной системой с нулевыми граничивши условиями. Уравнение для вычисления коэффициента в разложении для поперечной компоненты скорости W10 (p) снова отделяется, причем его решение зависит от значения коэффициента Р20 из системы С20 — (г4). В результате для нахождения W10 (p) получаем краевую задачу С0 — (г3):

dw10

• ^-00—;--+ ^-10—;--^3-00^w10 ⁺ W00 ^(-00 ^{- -}10) =

dpdp

= ^ [-00-10 (1 + 2ею) - (2— - рю (1 + ЕЮ)) (1 -+ 2

7                  Р00/    V Р00   Р00 V    Р00

p = ° : W10 = °; p ^ то : W10 ^ °.

При решении системы (15) методом Рунге-Кутты на поверхности крыла задавалась величина d-10/dp|₄=0 = -°. 19482 и были получены следующие значения коэффициентов: Р10 = -°.44577 и Дю = °.84°4°. На рис. 2 также приведен профиль продольной компоненты — -10 ( p )

В результате решения систем (13) и (15) для профиля продольной компоненты скорости с заданной точностью получаем

• - (p, г) = -00 (p) + -10 (p) г² + О ( e, ег², г⁴) . (Ъ)

Учитывая характер поведения функций -00 (p) и -10 (p) (рис. 2), можно отметить, что величина, пропорциональная напряжению трения в продольном направлении т_и = dn/dp|₄=0, будет иметь максимум в плоскости симметрии г = °, а, следовательно, профиль продольной компоненты скорости (17) становится более наполненным. Наибольшие изменения профиля (17) будут иметь место при значениях нормальной координаты ° < p < 2.

Зная решение краевой задачи С00 — О (1) и значение коэффициента рю = -°.44577 из решения системы Сю — (г2), можно перейти к решению краевой задаче 600 — О (г), описываемой уравнением и граничными условиями (14).

На рис. 3 приведен профиль для коэффициента W00 (p). Численные расчеты с использованием метода Рунге-Кутты показали, что в рассматриваемом случае существует решение с dw00/dp|₄=0 = °.142°6, при чем |w00 (p)| 6 °.2 для всех p. Следует отметить, что функция W00 (p) фактически является главным членом разложения первой производной от поперечной компоненты скорости по поперечной координате dw (г, p) /дг в плоскости симметрии крыла. Полученное решение можно трактовать как течение, в котором поперечная компонента скорости около поверхности крыла при ° < p 6 4.2 направлена от плоскости симметрии крыла, а при p > 4.2 она направлена к плоскости симметрии. Для точного определения направления течения в заданной точке поля течения необходимо вычислять знак коэффициента т = (ew - -г ) (1 - г²) из системы (10), который и определяет направление параболичности системы уравнений (10). При значении e ^ ° полученное решение в этом приближении может интерпретироваться как течение со стеканием к плоскости симметрии.

Краевая задача С20 — (г4) и ее решение:

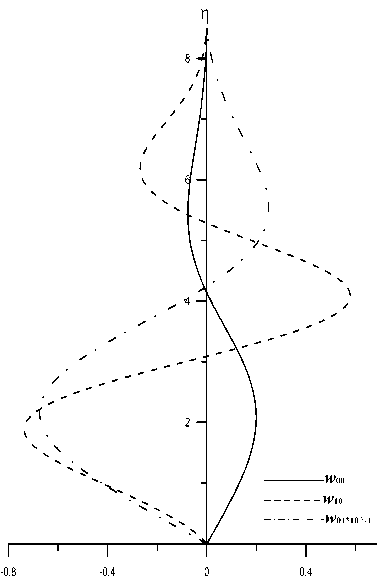
Рис. 3. Коэффициенты разложения в окрестности плоскости симметрии для поперечной компоненты скорости W00 (ц ), W₁₀ (ц) И 0.1W01 (ц)

• -«20   15      /9   510 А       ГО520   510 f    510 А]_

W - т«20 +   - Л “10 - Г500- 500Л 500)1 «00 + =01

4'00 -у²⁰ + <>20 -у⁰⁰ + 410 -у⁰ - 4«00 «20 + 2«10 («00 — «10 ) =

-ц       -ц-ц

=   -- -2«00«20 — «10 — 2 ( 1 + 4~— ) «00«10+

4?  L                     \500 /

, _л L 520   510 Л . 510 А А _{н 2} 3 , ^-2«20

+4 2---1 + — Щ - «00) + ——,18

V 500   500 V    500//          J-ц

-   3    Ли ^510 Л 16 510 АА 39 I (? - 1) (? +1) Г ' /2 .,

⁵²⁰ = ^- 25⁵⁰⁰ р^{1 +} 500 V ^- "3" 500) ) ^- 40 у ? к '   «^{20 +} «^{10) 11}

Д20 = 3 V^ к - 44 510 + 5 Л510 А 2 - 205201 , 130 V ? +1 |_       500     \500 /500 J ц = 0 : «20 = <20 = 0; ц ^ то : «20 ^ 0.

Уравнение для вычисления коэффициента w ₂₀ ( ц ) в разложении для компоненты скорости в поперечном направлении снова отделяется, но его решение зависит от значения коэффициента 53₀ из системы С₃₀ ~ (г⁶). В результате для нахождения коэффициента разложения W20 (ц) получаем краевую задачу С20 ^ (г5), которая для краткости не приводится, тж. в данной работе коэффициент W20 (ц) не вычисляется. При решении системы (18) на поверхности крыла задавалась величина -«20/-ц 1^=0 = -0.01298 и были получены следующие значения коэффициентов: 52₀ = -0.78254 и А2₀ = 0.78645. На рис. 2 приведены профили продольной компоненты — «20 (ц).

Зная решение краевых задач С00 ~ О (1), С00 ∼ О (г) и Ci0 ~ (г2) и значение коэффициента 520 = - 0.78254 из решения системы С20 ^ (г4), можно перейти к решению краевой задачи С^ ^ О (г3), описываемой уравнением и граничными условиями (16). На рис. 3 представлен профиль коэффициента W10 (у). Как показали численные расчеты с использованием метода Рунге-Кутты, в рассматриваемом случае существует решение при задании дш10/ду Ц=0 = -0.21730.

Используя полученные решения краевых задач Сю ~ О (1), С₁0 ~ (г²) и С20 ~ (г⁴), можно найти решения системы С30 ~ (г⁶), определив из этого решения значение коэффициента рзо- Используя это значение 530 и дополнительно решения систем СЦ ~ (г) и С Ц ~ (г³) можно решить систему С Ц ~ (г⁵) и найти коэффициенты W20 ( у). Таким образом, замыкая последовательно решения, можно найти необходимое число коэффициентов разложения для соответствующих функций течения. При этом будут последовательно решены краевые задачи, обозначенные условно в крайней левой колонке рис. 1, и в результате будут найдены главные члены разложения по параметру е.

Коротко опишем процедуру замыкания краевых задач для последовательного нахождения решений следующих систем. Имея решения С00 + СЦ, Сщ + СЦ, С20 и т.д., можно переходить к последовательному решению систем С01 ~ О (е), Сц ~ О (ег²) и т.д., условно обозначенных в средней колонке на рис. 1. В результате их последовательного решения получим соответствующие коэффициенты разложений при степенях, содержащих малый параметр е в первой степени. После нахождения решения краевой задачи С01 ~ О (е) и коэффициента 511 из решения системы Сц ~ О (ег²) можно вернуться к решению краевой задачи СЦ ~ О (ег) и найти профиль коэффициента W01 (у). Затем можно последовательно найти решения систем СЦ ~ О (ег³), СЦ ~ О (ег⁵) и т.д. В результате будут определены все необходимые коэффициенты разложений в краевых задачах, указанных в средней колонке рис. 1. После этого можно переходить к решению систем и нахождению коэффициентов разложений, содержащих малый параметр е², т.е. можно решать последовательно краевые задачи, условно обозначенные в правой колонке рис. 1, С02 ~ ^О (^е2)’ ^С12 ~ О (е²г²) и т.д. Как следует из схемы, приведенной на рис. 1, задание определенного числа членов разложения по степеням г (левая колонка) ограничивает количество членов разложения по степеням е. Максимальное количество членов координатно-параметрического разложения фактически будет определяться схематически треугольником (рис. 1). Далее последовательно рассматриваются краевые задачи для нахождения коэффициентов разложений, содержащих малый параметр е.

Краевая задача С01 ~ (е) и ее решение:

d"01 , "01 ,         _n d"01 ,     du,00      7 — 1          , d²"01

■ .4 ' w00 =0- ■    .    + ’    .    = - 2       "°1 +

3 /(7 + 1) (7 - 1) /“       ,,  .2 /2500501

501 = -4V------7------/0 "00"01dp’Аш = 3:   ■  500- у = 0 : "01 = "01 = 0; у ^ то : "01 ^ 0.

Уравнение для вычисления функции W01 (у) отделяется, но его решение зависит от значения коэффициента разложения рц из системы Сц ~ (ег2), который пока не известен. В результате получается краевая задача для определения члена для производной от поперечной компоненты скорости СЦ ~ (ег):

dw01dw00

"00—5--+ "с ,--"00W01 + W00 (W00 - "01) = dp-у

=     1 [(1 + 2510) "00„0, - (511 - 5015) (1 - "00)1 + •"

7          500             500   500 500/dy у = 0 : W01 = 0; у ^ то : W01 ^ 0.

При решении системы (19) методом Рунге-Кутты на поверхности крыла задавалась величина -" 01 /-у| _ч =0 = 0.08378 и были получены следующие значения коэффициентов: 501 = -0.24451 л А01 = -0.16454.

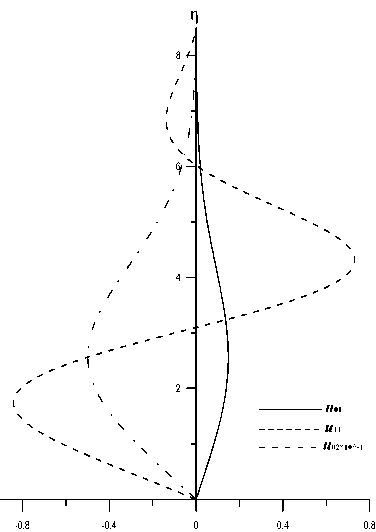
Рис. 4. Коэффициенты разложения в окрестности плоскости симметрии для продольной компоненты скорости Uqi (ц), и_П (ц) И П02 (ц)

На рис. 4 приведен профиль продольной компоненты — иоі (ц). Для рассматриваемых определяющих параметров профиль продольной компоненты скорости и индуцированное давление в плоскости симметрии г = 0 имеют вид и (ц) = иоо (ц) + иоі (ц) е + О (е2) , р = 0.81786 — 0.24451е + О (е2) .         (21)

Тогда из (21) видно, что при учете первого члена разложения по е происходит увеличение наполненности профиля продольной компоненты скорости и ( ц ) особенно около поверхности крыла.

После нахождения функции иоі ( ц ), тщ ( ц ), ро1 и Аоі из системы Соі ~ (е), зная решения краевых задач С_оо + СД и С_1о + С%, можно переходить к решению системы С_іі ~ (ег2).

Краевая задача С_іі ~ (ег2) и ее решение:

dvn

—;--+ 3 ww ац

-

|woо

+4 (иоі — 7иіі)

₊ Ріо

Роо

(wоо — иоі) + (

Ріо Роі

Роо Роо

Ріі

—      иоо = 0,

Роо

Ріі =

—3Роі

-

15 I (7 — 1) (7 +1)

∞

/   (2иоои_п + 2иіоиоі + W2Q) ац,

Аіі =

7 ²    [Роі /2 + Ріо ) — 2Ріі 1,

5 V 7 + 1 Роо Роо / Роо ц = 0 : иіі = гп = 0; ц ^ го : иіі ^ 0.

Уравнение для вычисления коэффициента в разложении для поперечной компоненты скорости wn (ц) снова отделяется, т.к. его решение зависит от значения коэффициента Р2і из системы С2і ~ (ег4). В результате для нахождения wі1 (ц) получаем краевую задачу СД ~ (ег3), которая из-за краткости не приводится.

При решении системы (22) методом Рунге-Кутты на поверхности крыла задавалась величина аиц/ац|7?=о = —0.61852 и были получены следующие значения коэффициентов Ріі = 0.34715 и Аң = —0.21199. На рис. 4 приведен профиль продольной компоненты — иіі (ц).

Зная решения краевых задач Coo + Coo и Co1 ~ (е) и значение коэффициента рц, можно вернуться к поиску решения системы C qi ~ (еz), описываемой уравнением и граничными условиями (20). На рис. 3 приведен профиль для коэффициента 0.1uo1 (у). Как показали численные расчеты с использованием метода Рунге-Кутты, в рассматриваемом случае существует решение с дц/ду |_ч=о = -4.4102. Завершив нахождение решения объединенной системы Си + С^, можно переходить к решению системы С02 ~ О (е²).

Краевая задача Co2 ~ (е2) и ее решение:

d«o2   «o2

w + ^ + uo1 =

0,

« d«o2 + « d«o1 + « d«oo = - 7 - 1 ,     «  + «2 \ + d2«o2

dy        dy        dy 47                ' dy²

P02 = — 3 ФТ—ДД!) [” 2    . + «2,⁾ d„, До2 = 1 J^ [4' ' - (^P01) ²

8 у 7       0o                            6V 7 + 1 [ Poo   VPoo/ у = 0 : «o2 = «o2 = 0; у ^ то : «o2 ^ 0.

Уравнение для вычисления коэффициента в разложении для поперечной компоненты скорости uo2 (у) снова отделяется, но его решение зависит от значения коэффициента P12 из системы С12 ~ (еД2). В результате для нахождения uo2 (у) получаем краевую задачу Co2 ~ (е2z), которая для краткости не приводится.

При решении этой системы методом Рунге-Кутты на поверхности крыла задавалась величина d«o2/dy|,?=o = -2.7835 и были получены следующие значения коэффициентов: Po2 = 8.31762 и Ao2 = 5.58908. На рис. 4 приведен профиль продольной компоненты 0.1«o2 (у).

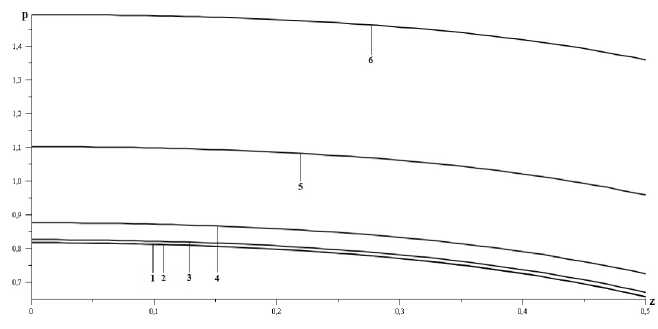
Рис. 5. Зависимость индуцированного давления   р (z)   по ко ординате z при е = 0.001, 0.01, 0.05, 0.1, 0.2, 0.3 (кривые 1-6) в окрестности плоскости симметрии

В результате проведенных расчетов определены следующие разложения:

«(ту, z) = «oo (у) + «1o (у) Z2 + «2o (у) Z4 + «oi (у) е+ +«11 (у) z2е + «o2 (у) е2 + О (z6, z4е, z2е2, е3) , « (у, z) = «oo (у) + «1o (у) z2 + «2o (у) z4 + «o1 (у) е+

+«11 (у) z2е + «о2 (у) е2 + О (z6, z4е, z2е2, е3) , u (у, z) = uoo (у) z + U1o (у) z3 + uo1 (у) zе + О (z5, z3е, zе2) ,            (24)

р (z) = 0.81786 - 0.44577z2 - 0.78254z4 - 0.24451е+

+0.34715z2е + 8.31762е2 + О (z6, z4е, zV, е3) ,

A (z) = 1.10074 + 0.8404z2 + 0.78645z4 - 0.16454е-

-0.21199z2е + 5.58908е2 + О (z6, z4е, zV, е3) , здесь соответствующие профили и^з (у) и w^ (ту) приведены на соответствующих рис. 2-4.

На рис. 5 приведено полученное распределение индуцированного давления для значений поперечной координаты 0 6 г 6 0.5 для параметров е = 0.001 (кривая 1), е = 0.01 (кривая 2), е = 0.05 (кривая 3), е = 0.1 (кривая 4), е = 0.2 (кривая 5), е = 0.3 (кривая 6). Следует отметить, что кривые 1 и 2 близки во всем диапазоне поперечной координаты г. Данные, приведенные на рис. 5, показывают, что в окрестности плоскости симметрии крыла имеет место локальный максимум давления и выполняется условие сходимости ряда для р (г, е) (12).

4.    Разложения в окрестности передней кромки крыла и определение собственного числа

Для исследования поведения функций течения в пространственном пограничном слое в окрестности передней кромки г = 1 треугольного крыла преобразуем краевую задачу (8) и введем новые переменные [3]:

У* = у* (1 + г)¹/⁴ , р . = р (1 + г)^-1/² , Аа = А (1 + г)³/⁴ ,

1 — г ду* Р а дг .

г** = г* (1 + г) ^1/4 + ( ew — иг )

Для рассматриваемой задачи переменные (25) не являются автомодельными переменными, но правильно учитывают поведение функций течения около передней кромки г = 1, т.к. переменные (25) будут приводить задачу к автомодельному виду, если рассматривать обтекание полубесконечной скользящей пластины в режиме сильного взаимодействия [2]. Учитывая, что в окрестности передней кромки тоже будет производиться разложение функций течения в ряды, преобразуем переменные (25) по аналогии с (9) так, чтобы в получающейся краевой задаче индуцированное давление р_а (г) оставалось в знаменателе только при члене с градиентом давления:

У а = У*Ра 1/2, г . = г ** р . ^/2 - j (ew — ги) (1 — г) р. ^.               (26)

После подстановки (25) и (26) в краевую задачу (8) она приводится к виду:

ди

ди

Ту- + Гау— = ^{дг     ду}а

У

-

дw

дw

Тщ- + Гау— = ^{дг     ду} а

дГ а

ду а

-

А а

т = ( ew

2у

-

У

-

-

иг ) (1

-

г),

(1 — и2

-

Ew2

) (2+г

(1 — г

Р а

2 dPa \ йг *

+

д2и

дУ2'

2У

(1 — и2

-

Ew2) (I + (1

-

г

Р а

) йРа \ йг

д2w

^{+ д} У2 ¹

4(Ew — иг) + (|

dw

-

ди дw , г + е + (ew дг дг

-

ги)— ^) (1 — г) ’ 2р а йг

= 0,

= — J ^У-^ ~ (1

VP^V 2 у 0_О

-

и2

-

Ew²) йу а , Р а =

У +1

( 4

-

г (1

-

. йА а 2

г)               ,

у_а = 0 : и = w = г_а = 0;   у_а ^ то : и ^ 1, w ^ 0.

Как и в работе [3], предполагается, что в окрестности передней кромки г = 1 решение не является единственным. Разложим индуцированное давление р_а в ряд следующего вида:

Р а (г) = ро + рі (1 — г)“ + ...                               (28)

Остальные функции, входящие в (27), представляются в виде рядов

/ = /о (Уа) + /1 (Уа) Р1 (1 — г)“ + ...,                         (29)

Ро где / = (u, w, va, Да).

Подставляя разложения (28) и (29) в систему уравнений и краевые условия (27) и собирая члены одного порядка по степеням, получаем соответствующие краевые задачи. Для нулевых членов разложения будем иметь краевую задачу:

Po =

dv_o d] a

duo vo3ZT = d]a dwo vo"T" = ' d]a

-

7 -

-

³ I ⁽7 + ¹⁾⁽7 - 1) 8V'

4 ( ew o - uo) = 0,

- (1 ^{- u} o ^- £^w2) ⁺

74— (1 ^{- u}o - EW2 ) ⁺

/ " (1 — uo 0

-

d² u_o ^d-n a , d² w_o

"^a,

^Ew2) "T] a , ^Д0 = 3^

Дт Po, 7 + 1

E a = о : uo = vo = wo = 0;

]_a ^ to : u_o ^ 1, w₀ ^ 0.

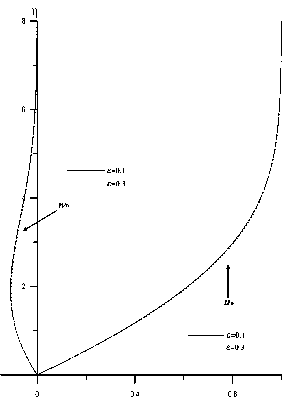
Рис. 6. Коэффициенты разложения в окрестности передней кромки для продольной — u₀ (]₀ ) и поперечной компонент скорости w₀ (]₀ ) для е = 0.1, 0.3

Для первых членов разложения получаем:

dv_i "]a

(a + 4) (ew i - ui) -

2 a (ew o - uo ) = 0,

du1du vo "У + v° "^ (ewo - uo) ui a =

7 - 1 Г               /.2    2\1 d² ui

—— [uoui + ewowi + a (1 - uo - ewo)J + —^, 27

dwidw

vo "һГ + v® -- (ew o - uo) wi a =

3 + 2a

3 + 4a

7 - 1

[uooui + Ewoowi + a (1 - uoo - ew^ ] +

d² w_i ^d] a ,

[" (1 - uo 0

-

Ew2) d]a =

-

∞

2 /   (uoui + Ewowi) d]a

Ді =-----До, i 6 +8a o,

]_a = 0 : ui = vi = w_i = 0;  ]_a >  to : u_i ^ 0, w_i ^ 0.

Для существования отличных от нуля первых членов разложений (28), (29) (pi/po = 0) должны существовать некоторые собственные значения a, при которых переопределенная система уравнений (31) имела бы решение.

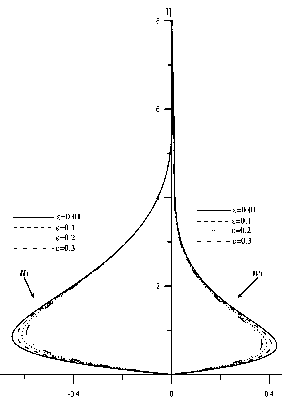
Рис. 7. Коэффициенты разложения в окрестности передней кромки для продольной — и1 (цо) и поперечной компонент скорости w1 (ц₀) для е = 0.01, 0.1, 0.2, 0.3

На рис. 6 приведены профили продольной и₀ ( ц_а ) и попе речной w_g (ц_а) компонент скорости для значений е = 0.1, 0.3, полученные в результате решения системы (30). Расчеты, проведенные для значений е <  0.1, показали, что функции ng (ц_а) и wg ( ц_а ) изменяются очень слабо, т.к. |wg ( ц_а )| = О (0.1), а в уравнения импульсов в градиентные члены входят величины порядка EW2 ( ц_а ).

На рис. 7 приведены профили для первых членов разложения для продольной п1 ( ц_а ) и поперечной w1 ( ц_а ) компонент скорости для значений е = 0.01, 0.1, 0.2, 0.3, полученные в результате решения системы (31). Численное интегрирование систем (30) и (31) показало, что для рассматриваемых определяющих параметров для значений 0.0001 6 е 6 1 для каждого е имеется только одно собственное значение а.

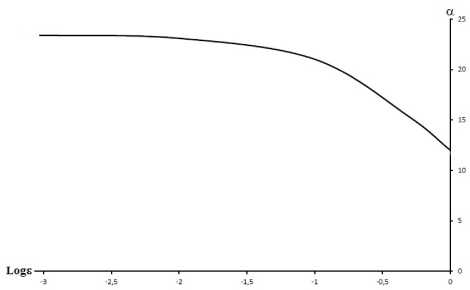
Рис. 8. Зависимость значения собственного числа а от параметра е

На рис. 8 приведена зависимость значения собственного числа а от значения параметра е. При е 6 0.01 собственные числа выходят на асимптоту а ~ 23.14. В рассмотренном диапазоне параметра е минимальные значения а ~ 11.997 достигаются при е = 1 (угол стреловидности передней кромки 45°). Следует отметить, что по порядку величины указанные собственные значения соответствуют значениям, приведенным в [3], где рассмотрен случай обтекания треугольной пластины при g_w = 0.5.

На рис. 9 приведена зависимость величины индуцированного давления pg на передней кромке от параметра е. При е 6 0.01 давление на передней кромке выходит pg ^ 0.812822. Увеличение параметра е приводит к уменьшению давления на передней кромке крыла.

На рис. 10 в качестве примера приведены зависимости р_а (%) = pg + р1 (1 — % ) ^а в диапазоне 0.01 6 % 6 1 для значений параметра е = 0.1, 0.3, 1 в случае, когда константа р1 = 1.

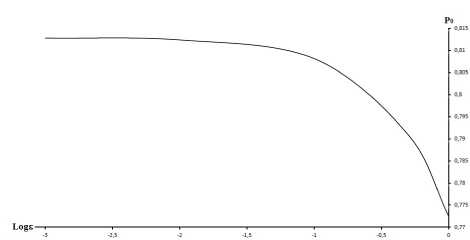
Рис. 9. Зависимость значения индуцированного давления на передней кромке ро от параметра е

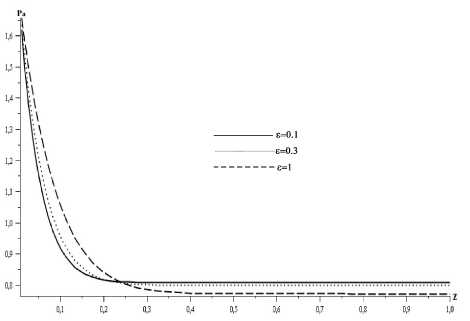
Рис. 10. Зависимость р _а (г ) для е = 0.1, 0.3, 1 при значении параметра р1 = 1

Увеличение параметра е (при этом происходит уменьшение собственного числа а) приводит к увеличению поперечного размера области влияния течения в плоскости симметрии крыла и большему возрастанию давления при приближении к плоскости симметрии крыла.

5.    Сращивание решений для определения индуцированного давления на крыле

Как показано в предыдущем разделе, решение вблизи передней кромки является неединственным [3], т.к. имеет место однопараметрическое семейство решений, зависящих от величины рі, входящей в (28) и (29). Отобрать нужное значение параметра рі можно в результате сращивания двух решений: решения (11) — разложение в окрестности плоскости симметрии крыла — и решения (28) — разложение в окрестности передней кромки г = 1. Учитывая, что сращивание решений будет происходить при некотором заранее неизвестном значении поперечной координаты г = г*, то для сращивания решений для индуцированного давления необходимо потребовать выполнения двух условий. Такими условиями могут быть равенство давлений и равенство производных от давления по поперечной координате для двух разложений при значении поперечной координаты г — г*. Так как при рассмотрении течения в окрестности передней кромки вводилось преобразование давления (25), то имеем следующие два условия в переменных (7):

^{р ( г} * ) — ⁽¹ + ^г * )    ^р а ^{( г} * ) ,

dp

dг

z = z *

d dг

[ (1 + г* )^1/2 Р а

( г*

z = z *

Учитывая полученные с заданной точностью разложения для давления в окрестности плоскости симметрии (24) и в окрестности передней кромки (28), из уравнений (32) полу- чаем следующие условия:

0.81786 - 0.44577^ - 0.78254^ - 0.24451е + 0.34715^2 е + 8.31762е² =

= (1 + ^z*^)1/2 ^^ро ^(е) + ^р 1 ^{(1 - z} * )“^(е)) ,

-0.89154г* - 3.13016z J + 0.6943z * е =

= 0.5(1 + z* )^-1/2

(po (е) + ( I - 21^ а (е)) pi (1 - z*Щ)) .

Задавая конкретное значение малого параметра е* и используя результаты расчетов, приведенные на рис. 8 и рис. 9, находим соответствующие значения а (е*) и ро (е*). Подставляя их в систему (33), находим значения параметра р₁ и поперечной координаты z*, при которой происходит сращивание решений с заданной точностью, соответствующие заданному параметру е*. Для нахождения неизвестных р₁ и z* использовался метод итераций.

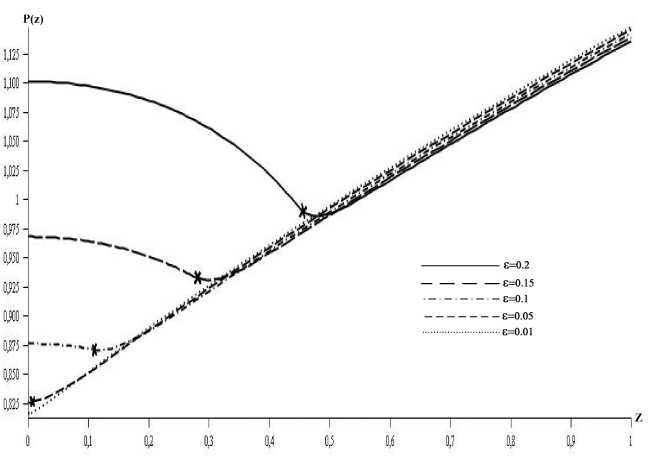
Рис. 11. Зависимость индуцированного давления р (z) по координате z на всем крыле при е = 0.01, 0.05, 0.1, 0.15, 0.2

На рис. 11 приведены полученные в результате сращивания распределения индуцированного давления р (z) по размаху крыла для значений малого параметра е = 0.01, 0.05, 0.1, 0.15, 0.2, где крестиками обозначены значения поперечной координаты z*, при которой происходило сращивание двух решений. На рис. 11 кривые для диапазона 0 6 z 6 z* построены согласно выражению р (z) = 0.81786 - 0.44577z2 - 0.78254z4 - 0.24451е + 0.34715z2е + 8.31762е2,    (34)

для z* 6 z 6 1 по формуле р (z) = (1 + z)1/2 (р0 (е) + р1 (1 - z)"(£)^. При значении параметра е = 0.01 из решения систем (30) и (31) имеем р0 (е = 0.01) = 0.8124 и а (е = 0.01) = 23.14, а тогда из решения системы (33) получаем координату сращивания z* (е = 0.01) = 0.005 и значение постоянной р1 (е = 0.01) = 0.00202. Данное решение показывает, что при обтекании треугольных крыльев с размахом s > 10 (е 6 0.01) на большей части треугольно го крыла в пограничном слое фактически реализуется течение, как на полубесконечном скользящем крыле, а влияние течения в плоскости симметрии на все течение очень слабое (р1 = 0.00202) и ограничено очень небольшой относительной областью течения в окрестности z = 0. При значении параметра е = 0.05 из (30) и (31) находим р0 (е = 0.05) = 0.81049

и а (е = 0.05) = 22.123, а тогда из решения системы (33) получаем координату сращивания г* (е = 0.05) = 0.008 и значение постоянной рі (е = 0.05) = 0.0153. Данное решение показывает, что при обтекании треугольных крыльев с размахом s ~ 4.47 (е = 0.05), как и в предыдущем случае, на большей части крыла в пограничном слое реализуется течение, как на полубесконечном скользящем крыле с другим углом скольжения, но влияние течения в плоскости симметрии на все течение увеличивается примерно до 3% от размаха крыла, и это связано с увеличением постоянной рі = 0.0153 фактически на порядок. При значении параметра е = 0.1 из (30) и (31) находим ро (е = 0.1) = 0.808146 и а ( е = 0.1) = 21.03, а тогда из решения системы (34) получаем координату сращивания г* ( е = 0.1) = 0.109 и значение постоянной рі (е = 0.1) = 0.221. В данном случае решение показывает, что при обтекании треугольных крыльев с размахом s ~ 3.16 (е = 0.1) влияние течения в плоскости симметрии на все течение значительно возрастает и составляет уже примерно 15% от размаха крыла. При значении параметра е = 0.15 из (30) и (31) находим ро (е = 0.15) = 0.80585 и а (е = 0.15) = 20.04, а тогда из решения системы (33) получаем координату сращивания г* (е = 0.15) = 0.28 и значение постоянной рі (е = 0.15) = 14.5. В данном случае решение показывает, что при обтекании треугольных крыльев с размахом s ~ 2.58 (е = 0.15) влияние течения в плоскости симметрии на все течение еще больше возрастает и составляет около 1/3 от размаха крыла, при этом постоянная рі (е = 0.15) = 14.5 возрастает практически на два порядка по сравнению со случаем е = 0.1. При значении параметра е = 0.2 из (30) и (31) находим р₀ (е = 0.2) = 0.803605 и а (е = 0.2) = 19.2, а тогда из решения системы (33) получаем координату сращивания г* (е = 0.2) = 0.456 и значение постоянной рі (е = 0.2) = 1961.5. В данном случае решение показывает, что при обтекании треугольных крыльев с размахом s ~ 2.24 (е = 0.2) влияние течения в плоскости симметрии на все течение еще больше возрастает и составляет более 1/2 от размаха крыла, при этом постоянная рі = 1961.5 возрастает практически на два порядка по сравнению со случаем е = 0.15. Проведенные исследования гиперзвукового обтекания теплоизолированного плоского треугольного крыла с малым углом стреловидности передней кромки на режиме сильного вязко-невязкого взаимодействия показали, что уменьшение размаха крыла приводит к значительному изменению характера обтекания. Так, при уменьшении размаха крыла с s ~ 4.47 д os ~ 2.24, т.е. примерно в два раза, происходит увеличение области влияния плоскости симметрии на все течение в пограничном слое более чем в 15 раз (с 3% до 50% от размаха крыла).

6.    Выводы

В результате исследования уравнений трехмерного пограничного слоя на плоском треугольном крыле с малым углом стреловидности передних кромок /3 << 1, обтекаемом гиперзвуковым потоком вязкого газа, показано, что в пограничном слое под действием индуцированного давления возникает течение в поперечном направлении, имеющее порядок w° ~ 'U^/ctg/3- Показано, что в этом случае для исследования течения в окрестности плоскости симметрии крыла можно построить координатно-параметрическое разложение для функций течения. Сформулированы краевые задачи для вычисления коэффициентов разложений и определена процедура их замыкания. Построено разложение для функций течения в окрестности передней кромки крыла. Сформулированы соответствующие краевые задачи и найдены собственные значения. Проведено сращивание решения для индуцированного давления в окрестности плоскости симметрии и решения в окрестности передней кромки. Проведенные исследования гиперзвукового обтекания теплоизолированного плоского треугольного крыла с малым углом стреловидности передней кромки на режиме сильного вязко-невязкого взаимодействия показали, что уменьшение размаха крыла приводит к значительному изменению характера обтекания.

Автор благодарит профессора Г.Н. Дудина за постоянное внимание к работе и полезные обсуждения. Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-00202).