Обзор графических методов статистического анализа генераторов псевдослучайных последовательностей

Генератор псевдослучайных чисел алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному) [1]. ГПСЧ широко используются в различных сферах человеческой деятельности. В частности, можно выделить следующие области применения:

п мобильная связь и космическая связь

П коды обнаружения и исправления ошибок п лотереи iz криптография

Если к первым трём пунктам критерии отбора генераторов псевдослучайных последовательностей могут допускать некоторые статистические закономерности, то к пятому пункту такое попросту недопустимо. В криптографии генераторы псевдослучайных чисел играют крайне важную роль и зачастую именно они обеспечивают криптостойкость того или иного алгоритма шифрования. Так как алгоритмы ГПСП являются детерминированными, то истинная случайность последовательности является задачей, которая на данный момент не решена. Суть работы хорошего ГПСП — это максимальная аппроксимация последовательности к истинно случайной. Ключевыми тестами для оценки работы ГПСП являются методы статистического анализа последовательности на её случайность. В данной работе будут рассмотрены графические тесты для статистического анализа ГПСП.

Гистограмма распределения элементов

В этом тесте производится оценка равномерности распределения элементов в исследуемой последовательности и определить частоту появления конкретного символа[2].

Описание теста: в полученной последовательности подсчитывается количество вхождений каждого элемента и на основе этих данных строится гистограмма[3].

Рисунок 1 демонстрирует успешное прохождение теста — элементы из заданного диапазона встречаются практически одинаковое количество раз.

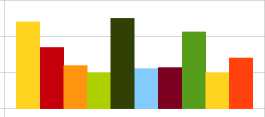
Рисунок 2 демонстрирует последовательность, которая не прошла данный тест, так как распределение элементов не равномерно.

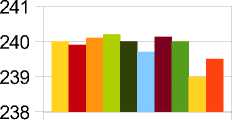
^___ Рисунок 1. Успешное прохождение теста ^{___ 9 _ 10 __} "Теория и практика современной науки"

Рисунок 2. Тест не про

^йден (^_8^_)^_20 ⁹ 6 ¹⁰

Проверка серий

В данном тесте оценивается равномерность распределения символов в исследуемой последовательности на основе анализа частоты появления нулей и единиц и серий, состоящих из n бит[3].

Описание теста: исходная последовательность представляется в двоичном виде. Производится подсчёт количества вхождений нулей, единиц, наборов из двух, трёх, четырёх элементов и т.д. На основе полученных значений строится график[3].

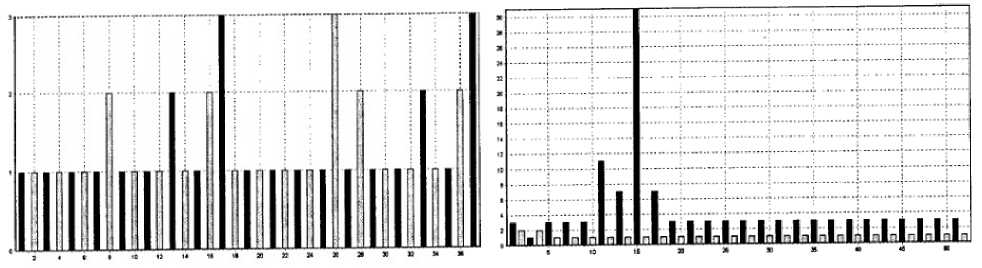
Рисунок 3 демонстрирует успешное прохождение теста — элементы из заданного диапазона встречаются практически одинаковое количество раз. Рисунок 4 демонстрирует последовательность, которая не прошла данный тест, так как распределение элементов не равномерно.

Рисунок 3. Тест пройден

Рисунок 4. Тест не пройден

Проверка на монотонность

Данный тест позволяет оценить равномерность распределения символов в последовательности на основе анализа длин участков невозрастания и неубывания элементов последовательности[2].

Описание теста последовательность графически представляется в виде следующих друг за другом непересекающихся участков невозрастания и неубывания элементов. В последовательности со статистическими свойствами, близкими к истинно случайной последовательности, вероятность появления участка неубывания или

невозрастания определённого размера зависит от его длины — чем больше длина, тем меньше вероятность (рис. 5). Иначе — последовательность не случайна (рис. 6)[3]

Рисунок 5. Тест пройден Рисунок 6. Тест не пройден. Вывод

Графические методы статистического анализа последовательностей являются весьма эффективными при выявлении существенных недостатков генерируемой последовательности. С их помощью можно быстро отбросить ГПСП, чьи результаты не удовлетворяют критериям Однако, графические тесты воспринимаются человеком, что не гарантирует их однозначность. Для более точных результатов используются статистические тесты, которые выдают численную характеристику последовательности и позволяют однозначно сказать, пройден тест или нет.