Обзор классических методов машинного обучения в контексте решения задач классификации

Машинное обучение - это область искусственного интеллекта, в которой изучаются методы построения алгоритмов, способных обучаться решению какой-либо задачи. Наиболее популярным является определение машинного обучения, данное Томом Митчеллом [1, с. 2]: «Говорят, что компьютерная программа обучается на основе опыта Е по отношению к некоторому классу задач Т, если качество решения задач из Т, измеренное на основе метрики Р, улучшается с приобретением опыта Е».

Машинное обучение позволяет решать большое число задач, которые в общем случае можно отнести к одной из следующих групп:

классификация – определение метки класса объекта по набору его признаков;

регрессия – прогнозирование значения некоторой количественной характеристики объекта на основе его признаков;

кластеризация – поиск групп объектов во всем множестве анализируемых данных [2, c. 102].

В данной статье будут подробно рассмотрены классические методы решения задач классификации.

Задача классификации

Классификация наряду с регрессией входит в обширный класс задач обучения с учителем (Supervised learning). В таких задачах обучение происходит на наборе пар «стимул-реакция». В контексте задачи классификации каждая такая пара – это объект, стимулом является набор признаков объекта, а реакцией – номер его класса. Алгоритму на основе имеющейся обучающей выборки объектов необходимо восстановить неизвестную зависимость между стимулом и реакцией. В случае успешного обучения обученный алгоритм сможет классифицировать объекты, не входящие в обучающую выборку, для которых известны только значения признаков.

• 1    Методы решения задач классификации

Множество методов алгоритмов машинного обучения можно условно разделить на:

• 1.    Базовые алгоритмы. Типичными представителями данного класса методов являются деревья принятия решений, метод ближайших соседей и метод опорных векторов.

• 2.    Ансамбли. Цель ансамблевых методов состоит в том, чтобы объединить результаты нескольких базовых алгоритмов. Этот подход позволяет осуществлять более точную классификацию, чем в случае использования базового алгоритма, однако настройка ансамблей алгоритмов является более вычислительно затратной. Типичные представители: метод случайного леса, AdaBoost и градиентный бустинг.

Ниже будут рассмотрены перечисленные методы.

• 1.1    Дерево принятия решений

Дерево принятия решений – непараметрический метод, используемый в машинном обучении, анализе данных и статистике. Дерево принятия решений — это дерево, в листьях которого записаны номера классов, а в остальных узлах — признаки, по которым различаются случаи. Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение [3].

Дерево принятия решений рекурсивно разбивает пространство объектов обучающей выборки таким образом, чтобы объекты с одинаковыми метками класса группировались в одном листе. Пример дерева принятия решений приведен на рисунке 1.

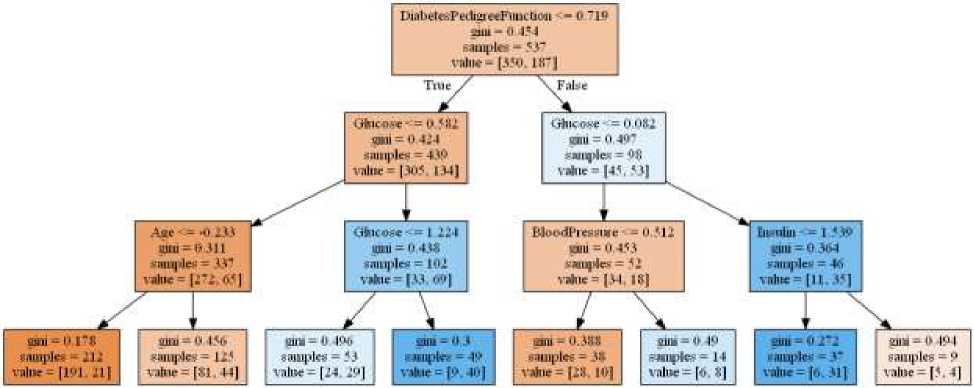
Рисунок 1 – Дерево принятия решений

• 1.2    Метод ближайшего соседа (nearest neighbor algorithm)

Классифицируемый объект x test будет отнесен к тому классу y i , к которому относится ближайший к нему объект x i обучающей выборки

Для повышения точности классификации применяют метод k ближайших соседей (рисунок 2). В этом случае объект xtest будет отнесен к тому классу, к которому относится большинство из k ближайших к нему объектов. Метод k ближайших соседей позволяет игнорировать различный шум и выбросы дан х обучающей выборки [4].

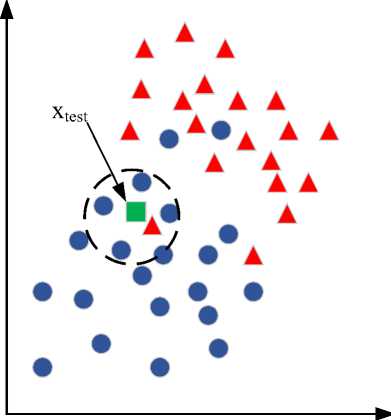
Рисунок 2 – Метод k ближайших соседей при k=5

1.3 Метод опорных векторов (Support Vector Machine, SVM)

Каждый объект обучающей выборки можно представить в виде точки в n-мерном пространстве. Идея SVM состоит в построении оптимальной гиперплоскости, выступающей в качестве поверхности решений, максимально разделяющей объекты разных классов. На рисунке 3 приведен случай двухклассовой (бинарной) классификации. Оптимальной гиперплоскостью в данном случае является прямая, максимально удаленная от объектов обоих классов. Объекты, расположенные максимально близко к оптимальной гипер оскости, будут называться опорными векторами [5].

Опорные векторы

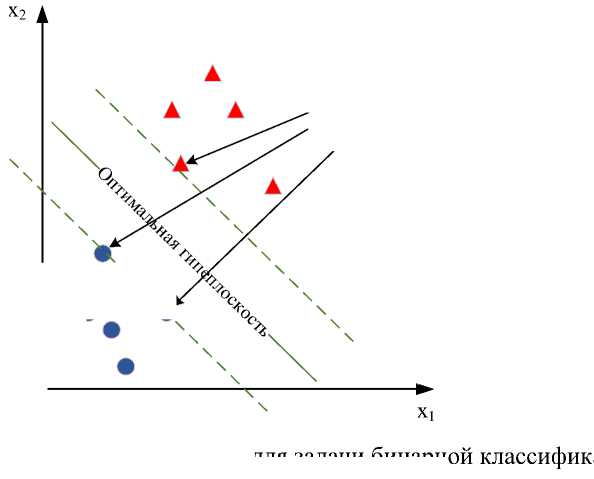
Рисунок 3 – Оптимальная гиперплоскость для задачи бинарной классификации

• 1.4    Случайный лес (Random forest)

Случайный лес – это способ построения ансамбля из m деревьев принятия решений, обученных на разных частях обучающей выборки, с целью преодоления проблемы переобучения отдельного решающего дерева. Алгоритм построения:

• 1.    Случайным образом отбирается 63% объектов обучающей выборки с возможными повторами данных.

• 2.    Строится дерево принятия решений на отобранной выборке. При разбиении дерева используются Vn случайных признаков объекта из первоначального набора из n признаков.

• 3.    Для каждого дерева на оставшихся 37% данных подсчитывается точность классификации.

Шаги повторяются m раз. После завершения построения случайный лес будет классифицировать объекты путем выбора того класса, который наиболее часто встречается среди ответов деревьев [6].

• 1.5    Ada boost

Основной принцип AdaBoost состоит в том, что каждый последующий базовый алгоритм ансамбля строится с учетом ошибок предыдущего классификатора. После построения каждого элемента ансамбля выполняется обновление весов, которые соответствуют важности каждого из объектов обучающей выборки для классификации. Веса каждого неверно классифицированного объекта возрастают, а веса правильно классифицированных объектов наоборот увеличиваются. Таким образом на следующей итерации классификатор «фокусирует своё внимание» на ошибках предыдущего алгоритма. В качестве основы для построения ансамбля часто используется дерево принятия решений [7].

• 1.6    Градиентный бустинг (Gradient Boosting)

Градиентный бустинг – это метод машинного обучения, который, как и Ada Boost, создает модель классификации в виде ансамбля слабых моделей, обычно деревьев решений. Он строит модель поэтапно, как и другие ансамблевые методы. На каждом шаге выбирается та модель, которая в совокупности с уже построенным классификатором позволяет минимизировать функцию потерь. Данный метод имеет высокую устойчивость к выбросам в данных, а также позволяет получить резкое повышение точности классификации по сравнению с базовыми классификаторами. Однако из-за последовательного процесса построения ансамбля градиентный бустинг не может быть распараллелен [7].

• 2 Тестирование методов

• 2.1    Набор данных

Описанные выше методы были протестированы на наборе данных Pima Indians Diabetes Database [8]. Целью набора данных является диагностическое прогнозирование наличия диабета у пациента на основе определенных измерений, включенных в набор данных. Набор включает следующие данные:

• -    Pregnancies – число беременностей (все данные принадлежат женщинам старше 21 года);

• -    Glucose – концентрация глюкозы;

• -    BloodPressure – артериальное давление (мм рт.ст.);

• -    SkinThickness – толщина кожи (мм);

• -    BMI – индекс массы тела (вес в кг/(рост в м)^2);

• -    DiabetesPedigreeFunction;

• -    Age – возраст (в годах);

• -    Outcome – целевая переменная (0 или 1).

• -    Таким образом необходимо обучить модель, верно определяющую значение параметра Outcome.

• 2.2    Результаты тестирования

При тестировании использовались реализации алгоритмов из Python-библиотеки Scikit-learn. Результаты тестирования на тестовом наборе данных приведены на рисунке 4.

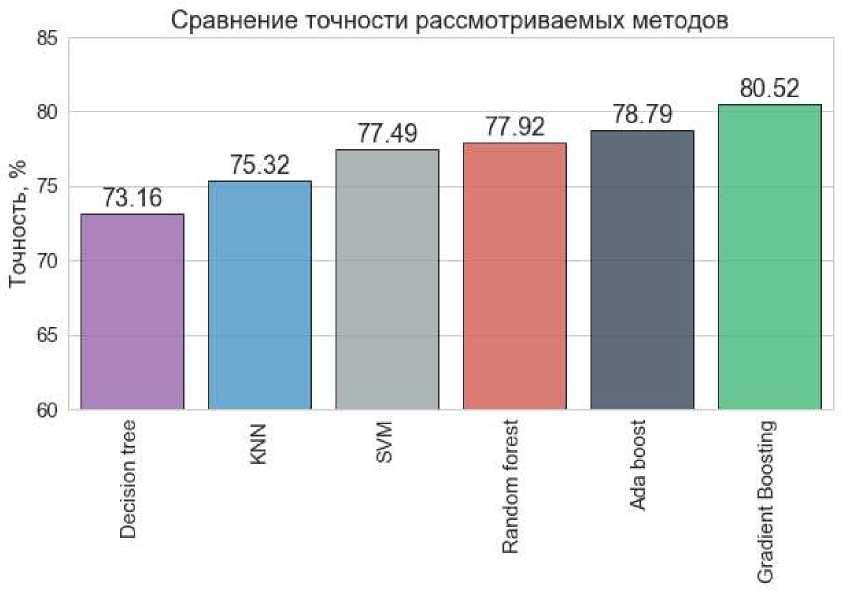
Рисунок 4 – Результаты тестирования

Значения, приведенные на диаграмме, позволяют утверждать, что ансамблевые методы способны повысить точность классификации. Наименьшую точность 73,16% показал алгоритм решающих деревьев, а наибольшую – градиентный бустинг, который позволил достичь 80,52% точности классификации.

Вывод

В данной статье были рассмотрены классические базовые, а также ансамблевые методы машинного обучения, применяемые в задачах классификации. По результатам тестирования можно утверждать, что ансамблевые методы позволяют достичь значительного повышения точности классификации по сравнению базовыми классификаторами. Однако, ни один из рассмотренных методов не сумел достичь высоких показателей точности, что говорит о необходимости предварительной обработки данных.