Обзор методов коллаборативной фильтрации

Коллаборативная фильтрация – один из наиболее распространенных методов построение прогнозов в рекомендательных системах. Она используется для предсказания «предпочтений» пользователей в той или иной предметной области на основе известных предпочтений других пользователей и ограниченного объёма данных о предпочтениях искомого пользователя. Метод основывается на предположении, что схожие по определенному критерию предпочтения можно использовать для взаимного дополнения, получая таким образом уникальные результаты рекомендаций.

В статье рассматриваются две основные группы методов коллаборативной фильтрации. Это корреляционные и латентные модели, проводится их сравнение, приводятся достоинства и недостатки.

Постановка задачи

Для исследования методов коллаборативной был проведен ряд экспериментов с открытым множеством данных (англ. dataset ) MovieLens , распространяемом на ресурсе [1], в котором содержится 24 миллиона оценок фильмов пользователями. Формат исходных данных для эксперимента представлен в таблице 1.

Таблица 1

Формат исходных данных

userId	movieId	Rating
1	101	5
1	102	2
1	103	3
2	101	5
2	105	4

Здесь userId – идентификатор пользователя, movieId – идентификатора фильма, rating – численная оценка по пятибалльной шкале, выставленная фильму пользователем.

Анализ работы алгоритмов производился следующим образом. Из исходного массива данных в 24 миллиона записей выделялась случайным образом тестовая выборка, в которую включалось 30% данных от исходного размера массива. На оставшихся 70% производилось обучение модели и строился прогноз оценок (значение столбца rating для данного пользователя и данного фильма) для включенных в тестовую выборку записей. Основной метрикой работы алгоритма коллаборативной фильтрации является расхождение предсказанных оценок с реальными оценками пользователей из тестовой выборки. В качестве такой метрики было выбрано значение RMSE (root-mean-square error, среднеквадратической ошибки), вычисляемое по следующей формуле:

RMSE = - где Pi – предсказанная i-ая оценка, Oi – её реальное значение, i – общее число оценок.

Корреляционные модели

В этих моделях для построения прогнозов используется корреляция между оценками пользователей. Исходные данные представляются в виде матрицы, строками которой являются пользователи, столбцами – оцениваемые объекты (в рассматриваемой предметной области – фильмы). Далее можно использовать два подхода, описанные в работе [2].

Первый подход – поиск «от пользователей». Схема работы метода представлена на рис. 1. В этом методе выполняется вычисление корреляции между строками матрицы. Для данной строки u₀ ищутся строки, значение корреляции с которыми для данной строки максимально. Отсутствующие в строке u₀ значения оценок из максимально коррелирующих строк добавляются в u 0 . Для эффективной работы этого метода необходимо, чтобы искомая строка u₀ была частично заполнена, в противном случае поиск корреляции будет невозможен. Эта особенность приводит к так называемой проблеме «холодного старта»: рекомендательная система не может работать с новыми пользователями.

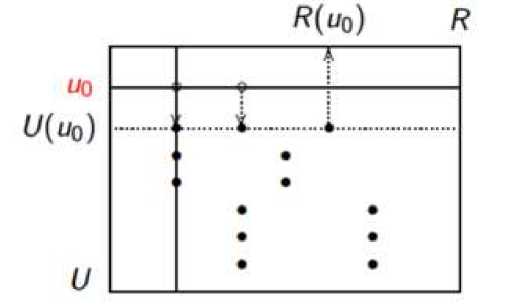
Рис. 1. Схема работы корреляционной модели подхода «от пользователей»

Корреляция для двух строк оценок (х 1 , „., x_m) и (y 1 , „., y_m) вычисляется по формуле:

_     Z™i⁽x_z -х⁾⁽У - У)     _ cov(x,y)

^{Г ху} ~ VS = = (yr-3V  ^sR

Альтернативный подход выполнения коллаборативной фильтрации на основе корреляции – поиск «от объектов». Схема работы метода представлена на рис. 2. В этом методе ищется корреляция не между строками матрицы, а между столбцами, т.е. происходит поиск похожих объектов, а не похожих пользователей. С технической точки зрения этот метод эквивалентен поиску от пользователей, но он позволяет рекомендательной системе работать с новыми пользователями, выдавая релевантные рекомендации при небольшом количестве оценок. Однако, по аналогичным причинам данный подход не может работать с новыми объектами (так как невозможно найти корреляцию для пустого столбца).

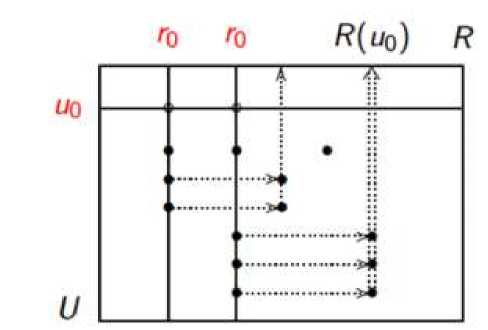
Рис. 2. Схема работы корреляционной модели подхода «от пользователей»

Оба варианта корреляционного поиска имеют общий недостаток. В обоих случаях для работы алгоритма требуется нахождения всего массива данных в оперативной памяти компьютера, что может быть затруднительно при работе с большими объёмами данных. Использовавшийся для экспериментов набор данных имел размер около 1 ГБ, что может быть превысить полный объём оперативной памяти современной ЭВМ.

Корреляционная коллаборативная фильтрация выполнялась с помощью открытого фреймворка GraphLab , написанного на языке программирования C++ [3].

Вычисления производились на следующей конфигурации: ЦПУ Intel Core i5-5200U 2,2 GHz, 8 GB RAM, HDD.

Время вычислений составило приблизительно 5 минут, полученное значение среднеквадратической ошибки: 0,96.

Латентные модели

Латентные модели основаны на введение промежуточного пространства, в котором рассматриваются характеристики пользователей (users) и предметов (items). Корреляционные модели строятся только на основании явных предпочтений пользователей. Главный их недостаток – необходимость хранить матрицу предпочтений. Введение промежуточного пространства позволит сохранить объём хранимых данных. В общем случае латентные модели могут основываться не только на явных предпочтениях, но и на неявных. В нашем случае к явным предпочтениям относятся оценки, которые ставятся пользователями фильмам. К неявным, например, можно отнести время просмотра веб-страницы с фильмом, время просмотра самого фильма, и т.п.

Метод альтернативных наименьших квадратов (ALS)

Метод альтернативных наименьших квадратов (англ. Alternative Least Square – ALS ) основывается на матричной факторизации, т.е. представлении исходной матрицы в виде произведения матриц. Для этого выбирается небольшое число k (~10). Путём обобщения исходных данных, каждый пользователь в дальнейшем будет характеризоваться вектором x_u, каждый товар – вектором y i . Эти вектора называются факторами. Если U – это матрица факторов для пользователей, P – для продуктов/объектов (в нашем случае фильмов), то матрица рейтингов может быть определена как R ~ U^TР. Наглядная интерпретация представлена на рис. 3.

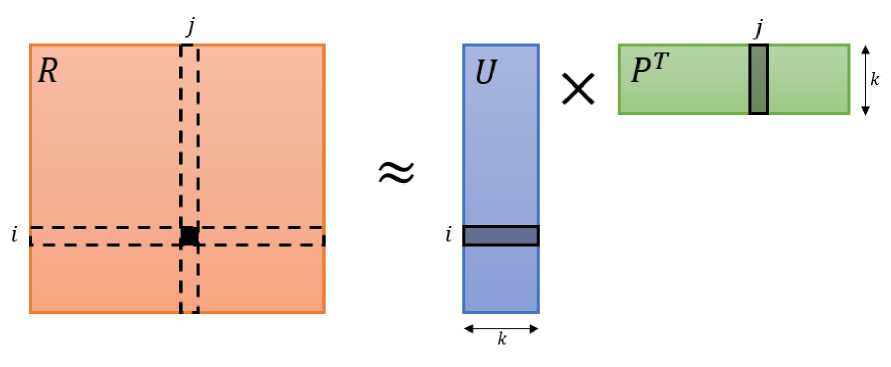
Рис. 3. Наглядная интерпретация разложения матрицы рейтингов

В конечном итоге мы хотим предсказать рейтинг, который поставит пользователь u фильму p . При обучении модели нашей целью является минимизация ошибки, т.е. отклонения предсказанного результата от реально. Это можно выразить следующей формулой:

mln   У   (г ху    £—1   и

—

^ ? У р ) 2 + ( ^H^ u H² +

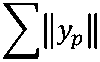
r_U p Observed                  \ и           р       /

Детальное пояснение формулы представлено в работе [4]. Стоит заметить, что в общем случае решение данной проблемы представляет собой

NP -полную

переменных

задачу. Однако, если поочерёдно фиксировать набор из U и P [5], то задача решается значительно проще. В этом

заключается

метод альтернативных наименьших квадратов

( ALS ). Формулы

после фиксирования множества переменных из U и P следующих формулах.

представлены в

максимального

^и = ( ^ ’ УрУр + ^к)    ^ ’ ^ирУр rup^ru*

ур = (у rup^r*p

^r up ^^r u*

^и^и + ^к)    ^ ’ ^ир^и rup ^r*p

Алгоритм обучает модель либо до достижения количества итераций, либо до заданного квадрата ошибки. В работе [6] автор приводит асимптотическую сложность обновления одной строки матрицы U как О(пик2 + к3), где nu - это количество фильмов, оценённых пользователем и. Для обновления матрицы P она составляет О(прк2 + к3), где np - количество пользователей, которые оценили фильм p.

Преимущества и недостатки ALS

Метод альтернативных наименьших квадратов обладает рядом преимуществ в сравнении с корреляционными моделями. Во-первых, не требуется хранить в памяти матрицу рейтингов. Как было показано выше, рейтинг вычисляется на основе двух матриц U и P, размерностью Nu X к и Nр X к, соответственно. Во-вторых, обучение модели может быть распределённым. Под распредёленностью понимается, что обучение производится на нескольких серверах одновременно. Это позволяет сократить объём хранения данных на одной машине и увеличить скорость обучения. Более подробно об этом рассказывается в работе [6]. В-третьих, алгоритм быстро сходится. Для обучения модели требуется порядка 10-20 итераций. К недостаткам можно отнести сложность понимания метода и техническую реализацию метода.

Реализации ALS

Поскольку метод ALS хорошо масштабируется на несколько серверов, то его реализуют популярные фреймворки распределённой обработки данных, такие как Apache Spark [7] и Apache Flink [8]. Каждый из них имеет интерфейс ( API ) для некоторых языков программирования ( Java, Scala, Python ).

В рамках работы использовался Apache Spark в конфигурации одного ноутбука. Технические характеристики ноутбука следующие: Intel Core i7-3612QM 2,10 GHz, 8 GB RAM, 256 GB SSD . Производился анализ зависимости процента предсказанных оценок от количества факторов. Построенный график представлен на рис. 4.

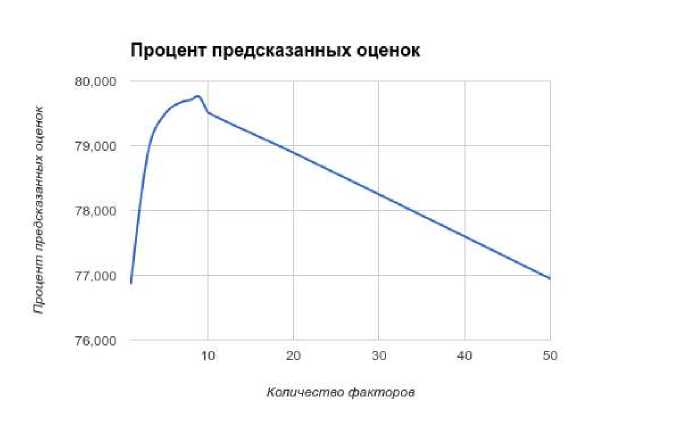
Рис. 4. Зависимость процента предсказанных ошибок от количества факторов

В ходе работы было установлено, что наибольший процент предсказаний достигается при 9 факторах. Для обучения использовалось 10 итераций. При этой характеристике RMSE = 0,8443, процент верно предсказанных оценок 79,71%. Как можно заметить по графику на рис. 4, при увеличении количества факторов модель снижает свои качества, время обучения возрастает. Зависимость времени обучения от количества факторов показана на рис. 5.

Зависимость времени обучения от факторов

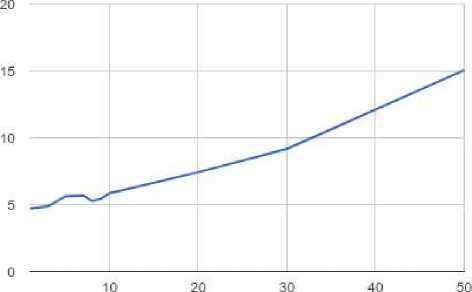
Количество факторов

Рис. 5. Зависимость времени обучения от количества факторов

Заключение

В статье рассмотрены некоторые методы коллаборативной фильтрации, применяемые в рекомендательных системах. Произведено сравнение корреляционных моделей, основанных на подходах «от пользователей» и «от объектов». Основные недостатки корреляционных моделей: не работают для новых пользователей, т.к. новые пользователи не поставили оценки объектам, а новые объекты не имеют оценок; требовательны к потребляемой памяти, т.к. требуется хранить матрицу оценок. Данный тип модели реализуется в GraphLab . Латентные модели лишены перечисленных недостатков. Необходимость хранения матрицы оценок решается матричной факторизацией, проблемы «холодного старта» – путём выявления неявных предпочтений пользователя. Метод ALS хорошо работает в распределённых системах, реализуется в Apache Spark и Apache Flink и показывает более приемлемые результаты в сравнении с корреляционными методами.