Обзор методов оптимизации траекторий космических аппаратов с использованием дискретных множеств псевдоимпульсов

Оптимизация траекторий космических аппаратов (КА) является предметом интенсивных исследований [1–8]. Имеется два основных типа методов оптимизации траекторий: непрямые и прямые, или их комбинации. Непрямые методы приводятся к решению двухточечной краевой задачи на основе принципа максимума Л.С. Понтрягина [6, 8]. В такой краевой задаче неизвестными являются сопряженные переменные, которые имеют высокую чувствительность и затруднения в поиске начального приближения. Прямые методы преобразуют задачу к форме параметрической оптимизации, которая решается, как правило, с помощью нелинейного программирования [8].

Автором совместно с А.В. Соколовым был разработан метод расчета оптимальных многовитковых межорбитальных перелетов с малой тягой на околокруговых орбитах с использованием трансверсальных маневров ограниченной продолжительности [3]. Метод использует классическое линейное программирование. В основе его математического представления лежит расширение пространства управляемых переменных за счет введения трансверсальных псевдоманевров противоположных направлений. Число неизвестных переменных при этом достигало нескольких сотен. Наиболее известным методом решения задач линейного программирования является симплекс-метод, однако он не обладает полиномиальной сходимостью, и его использование для задач высокой размерности (десятки, сотни тысяч переменных) затруднительно.

В 1990-е гг. линейное программирование претерпело революционные изменения, связанные с разработкой алгоритмов с полиномиальной сходимостью, известных как алгоритмы внутренней точки [9], которые обеспечивают более высокую эффективность, чем классический симплекс-метод. Это дало возможность разработки методов оптимизации траекторий КА с использованием линейного программирования высокой размерности. Рассматриваемые методы основаны на двух идеях. Первая — хорошо известная дискретизация траектории на малые сегменты. Вторая идея является ключевой и основана на близкой к равномерной дискретной аппроксимации пространства управления (т. е. направления и величины тяги) множеством псевдоимпульсов с ограничением в виде неравенства для каждого сегмента. Статья является обзором работ автора [10–21], в которых разработаны новые методы оптимизации траекторий различных типов КА.

Базовый метод для задач без ограничений

Движение КА представляется в виде точечной массы, имеющей ограниченную силу тяги, направленную по единичному вектору е ( e ^T ⋅ e ≡ 1). Уравнения движения КА:

d Y dt

= f [Y, P(t), M(t), e(t), t], где YT(t) = [rT(t), VT(t)] — вектор состояния КА; r(t), V(t) — радиус-вектор и вектор скорости, соответственно; t — время; P — сила тяги; M — масса КА. Краевые условия для траектории: F[Y(tf)] = Pf, где tf — заданное время перелета и Pf — вектор целевых значений размерностью s.

Предположим, что интервал перелета КА [0, t_f ] разбит на n малых, в общем случае неодинаковых и/или неявно заданных, сегментов ∆ t_i = t_{i + 1} – t_i , и известны приближенные значения функции F ( t_i ) в опорные моменты времени t_i . Считаем, что на каждом сегменте сила тяги P ( t_i ) и ее ориентация e ( t_i ) постоянны, тогда для краевых условий можно записать приближенное соотношение:

n

Pf( tf) = p*( tf) + z i - 1

d F ( t ) P ( t ) e ( t ) Nt

∂ a      m

г

=p;( tf)+z        a( t)a t., f f i-i     da         i i где Pf*(tf) — значение краевых условий на невозмущенной траектории КА в момент tf; dF/da — матрица частных производных; a — вектор реактивного ускорения.

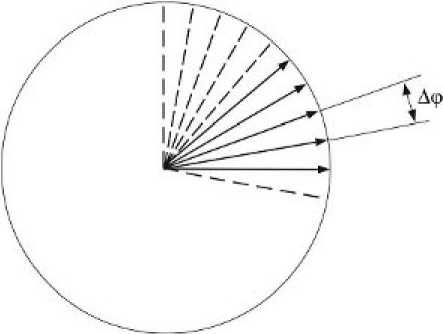
При ориентации вектора тяги в некоторой плоскости на любом сегменте i его направление может быть произвольным, и время работы двигателя не должно превышать длительности этого сегмента A t , , а приобретаемый на этом сегменте импульс скорости будет не более A V max = a p max A t ( a p max — максимальное ускорение тяги). Возможные направления вектора тяги представим в виде дискретного набора ориентаций, образованного делением диапазона [0, 2п] на малые углы Аф = 2п/ к (рис. 1, а), где к — число псевдоимпульсов. В оптимальном решении не может быть более двух ненулевых смежных псевдоимпульсов, поскольку сумму несмежных псевдоимпульсов всегда можно заменить двумя смежными псевдоимпульсами, имеющими наименьшую сумму (рис. 1, б) [10].

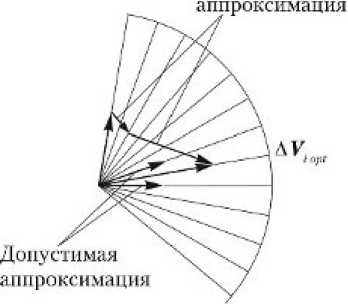
Тогда оптимальный импульс можно представить суммой k AV. f = ЕАVjе(j i opt 1 i i с ограничением на сумму характеристических скоростей псевдоимпульсов j = k ∑ ∆Vi( j ) ≤ 1. j = 1

Оптимальный импульс будет суммой ближайших псевдоимпульсов (рис. 1, б).

Подобным образом можно рассмотреть пространственный случай [10, 13].

Для вектора неизвестных неотрицательных переменных размерностью ( n х к )

Х^т = [А V ⁽¹⁾ , А V <², ..., А V*

АV(1), АV(2), .... АV(k>, .... АVnk>], включающего все псевдоимпульсы на всех сегментах, можно записать линейное неравенство:

A X ≤ b ,               (1)

где А — матрица размерностью n х( n х к ) (показаны только ненулевые элементы):

1 11...1 2 _k

A =

111...1

k

n.

111...1 k n×k

Вектор b T = ^{[ А} V _lm ax , ^А V 2__max , ^А V^ .... A V n _-1max , A V n max ] имеет размерность n . Краевые условия примут вид

A P f = P f - Р * = A e X ,             (2)

где А е — матрица размерностью s х( n х к ):

	' д F 1	д F 1	д F 1	д F 1	д F 1	д F 1	д F 1	д F 1	д F 1 "
	д V (1)	д V (2)	д V ( k ),	д V 2 1 )	д v < 2)	дv < k ) ,	д V (1) 1 n	д V (2) n	д f ( k ) n 3
		k			k			k
	д F 2	д F 2	д F 2	д F 2	д F 2	д F 2	д F 2	д F 2	д F 2
A =	14	дv(2)	д ^ 3)	д v 2 (1)	► • д v ( 2)	> •                                  • д V 2 ( 3 k )	• • д v (1) 1 n	► • д V (2) n	д F ( k ) n 3	.      (3)
e		k			k			2 k
	д F s	д F s	д F s	д F s	* * * • д F s	1 д F s	► • д F s	* * * • д F s	д F s
	д V (1)	д v (2)	д V 3	д V(1)	► • д V(2)	• •                                   • д V 2k)	► • д V (1) n	► • д V (2) n	“    д F ( к ) n
	L 1	k			k			k	3 J

Минимизируемой функцией является суммарная характеристическая скорость. Определим вектор коэффициентов q^T = [1 1…1 1] из ( nхк ) элементов для равномерных сегментов (все элементы равны 1). Тогда проблему оптимизации траектории можно сформулировать как задачу классического линейного программирования: найти вектор Х , минимизирующий линейный функционал J = min( q^T · X )

при линейных ограничениях в виде неравенства (1), равенства (2) и неотрицательных значениях всех элементов вектора Х : 0 < А V ( j < A V _max . В подобной формулировке задача имеет весьма высокую размерность. Однако, по своей структуре матрица А является разряженной, и современное программное обеспечение, например MATLAB ® , имеет эффективные алгоритмы вычислений с разряженными матрицами.

а)

Рис. 1. Псевдоимпульсы в плоскости: а — возможные ориентации; б — оптимальные ориентации

11сдопустимая

б)

Формально при решении задач с дискретизацией траектории по времени каждый сегмент рассматривается независимо от других, поэтому полученное решение требует специальной обработки. Критерием включения в обработку является наличие ненулевых компонент вектора Х . При этом для выбранных компонент вектора Х , относящихся к одному сегменту, уточняется ориентация вектора тяги и ее суммарный уровень. Далее в непрерывные маневры объединяются все последовательности смежных сегментов с ненулевым уровнем тяги. Таким образом может быть получен конечный набор непрерывных маневров. Рис. 2 иллюстрирует этот процесс.

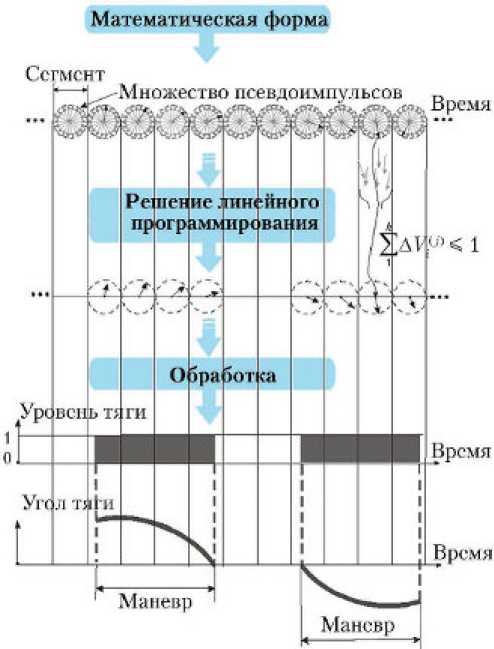
Рис. 2. Обработка решений линейного программирования

Оптимизация траекторий с ограничениями

Реальные траектории КА часто требуют удовлетворения не только терминальных условий, но также и некоторых специфических требований. Например, могут иметься следующие ограничения:

• •    ограничения для внутренних точек траектории в форме краевых условий или неравенств;

• •    ограничения, связанные с суммарным временем работы двигателей на некоторых подинтервалах;

• •    ограничения или предпочтительность по направлениям силы тяги, интервалам маневрирования;

• •    могут использоваться многорежимные двигательные установки с высокой, средней и/или малой тягой;

• •    другие операционные ограничения.

В представленных методах очень важно наличие гибких возможностей по расчету и проектированию оптимальных траекторий с различными требованиями и ограничениями. Для таких комплексных случаев необходимо расширение и/или модификация базовой формы (т. е. преобразование матриц А , А_е , вектора весовых коэффициентов q , множества сегментов и/или множеств псевдоимпульсов) [13].

Каждое ограничение в виде равенства F _IPT [ Y ( t_{f IPT} )] = P _IPT размерностью l во внутренней точке траектории требует l дополнительных строк в матрице A_e (3). Ограничения неравенства требуют расширения матрицы А [13].