Обзор программных комплексов и результатов расчетно-экспериментальных исследований и оптимизации характеристик систем с термоэмиссионным преобразованием энергии

АО «ГНЦ РФ–ФЭИ» обладает уникальными компетенциями в области физико-технического обоснования разработки и эксплуатации космических ядерных энергетических установок (КЯЭУ) с прямым преобразованием тепловой энергии в электричество, включая методы электротеплофизического расчета характеристик термоэмиссионного электрогенерирующего элемента (ЭГЭ) и электрогенерирующего канала (ЭГК) в целом, нейтронно-физические расчеты и оптимизацию структуры активной зоны и радиационной защиты. Физические основы, заложенные при обосновании характеристик КЯЭУ первого поколения В.Я. Пупко, Ю.С. Юрьевым, В.А. Малыхом, А.А. Дубининым и другими, в настоящее время подтверждаются и углубляются разработкой и применением современных расчетных комплексов и новейших математических методов оптимизации и поиска решений. Так, вместо одномерного упрощенного расчета характеристик ЭГЭ/ЭГК (комплекс TFEDM ) применяется трехмерный детальный расчет всего ЭГК ( COMSOL –ЭГК), вместо гомогенного расчета активной зоны и отдельного, не учитывающего проникающие элементы расчета радиационной защиты, применяются единые трехмерные расчетные комплексы, позволяющие учитывать гетерогенность и все особенности геометрии активной зоны и радиационной защиты, реализующие метод Монте-Карло (ММК) (в частности, программные комплексы MMKFK -2, MCNP ). Совместное применение перечисленных комплексов при расчетном обосновании характеристик проектируемых КЯЭУ позволяет наиболее полно исследовать пространство возможных решений и находить лучшие из них.

Для определения выходной электрической мощности КЯЭУ необходимо провести электротеплофизический расчет характеристик ЭГЭ/ЭГК. Одними из основных исходных данных для этого расчета являются значения тепловыделения в топливе. Такие исходные данные предоставляет нейтронно-физический расчет характеристик активной зоны, который, в первую очередь, определяет критические параметры активной зоны, запас реактивности реактора на кампанию и т. д. Зная габариты активной зоны, ее тепловую мощность и расположение органов регулирования, можно проводить расчет радиационной обстановки вокруг реактора и оптимизационные исследования в обоснование массогабаритных характеристик теневой радиационной защиты. В конечном итоге масса и габариты радиационной защиты, пространственное расположение отсеков космического аппарата с оборудованием определяют облик ядерно-энергетической установки, ее конкурентоспособность при сравнении характеристик КЯЭУ с другими типами ядерных энергоустановок с различными методами преобразования тепловой энергии в электрическую, в т. ч. и солнечными энергетическим установками.

методы расчета тепло- и электрофизических характеристик термоэмиссионных электрогенерирующих систем

С 1960-х гг. начали развиваться методы расчета тепло- и электрофизических характеристик ЭГК и термоэмиссионного реактора-преобразователя (ТРП) в целом. Спецификой этих методов является то, что приходится совместно решать тепло- и электрофизические задачи, так как термоэмиссионный ЭГК является одновременно ядерным твэлом и электрогенератором.

Конечной задачей тепло- и электрофизического расчета ТРП является получение его выходных вольтамперных характеристик (ВАХ), т. е. зависимости электрического тока от напряжения при заданной тепловой мощности реактора. Знание ВАХ позволяет определить электрическое напряжение и ток, выходную электрическую мощность и эффективность (КПД) преобразования тепловой энергии ТРП в рабочем режиме. Одновременно необходимо определить значение максимального уровня температуры эмиттеров ЭГК в активной зоне реактора-преобразователя, который не должен превышать предельно допустимого значения для данного материала эмиттерной оболочки. Однако, для того чтобы получить эти важнейшие выходные характеристики ТРП, состоящего из сотен ЭГК, соединенных в сложную электрическую цепь и находящихся в активной зоне реактора при различных уровнях плотности тепловыделения, необходимо провести целую серию теплоэлектрофизических расчетов единичного ЭГК при различных значениях тепловыделения, давления пара цезия в межэлектродном зазоре (МЭЗ) и ряда других внешних параметров. В настоящее время это стало возможным благодаря развитию информационных технологий и численных методов анализа. Широкое распространение получили интерактивные программы графического представления результатов расчета, основанные на решении краевых задач математической физики с помощью метода конечных элементов, такие как ANSYS, COMSOL, SolidWorks и др. [1].

Основные уравнения математической модели тепло- и электрофизических процессов, протекающих в единичном ЭГЭ термоэмиссионного ЭГК, были получены Ю.С. Юрьевым в ходе работ по созданию термоэмиссионной КЯЭУ «ТОПАЗ» [2]. Дальнейшее развитие методов численного решения системы нелинейных уравнений ЭГЭ проводилось В.А. Ружниковым [3–5], А.А. Шиманским [6], В.В. Синявским, Ю.В. Бабушкиным, В.П. Зиминым [7–10], В.А. Линником [11], Е.Г. Виноградовым [12] и др.

Первоначально из-за отсутствия достаточно мощных вычислительных средств разрабатываемые методы расчета тепло- и электрофизических характеристик ЭГК основывались на аналитическом решении системы уравнений ЭГЭ, что приводило к необходимости упрощения математической модели. В частности, приходилось вводить допущения о линейности локальной ВАХ термоэмиссионного преобразователя (ТЭП), постоянстве температуры коллектора и плотности эмиссионного тока по длине ЭГЭ [2]. При этих допущениях уравнение теплопроводности для коллектора вообще исключалось из математической модели, а уравнение теплопроводности для эмиттера при условии линеаризации члена, описывающего теплопередачу излучением, и уравнение для межэлектродного напряжения становились линейными и допускали аналитическое решение. Позднее для решения нелинейного уравнения теплопроводности для эмиттера были применены вариационные методы и метод Галеркина [11], позволяющие более точно рассчитать распределение температуры по длине эмиттера.

Последующий прогресс в развитии расчетных методов исследования ВАХ ЭГК был связан с разработкой численных методов решения системы нелинейных дифференциальных уравнений ЭГЭ [3–6]. Тем не менее, используемая при расчетах математическая модель тепловых и электрических процессов ЭГЭ, даже при некоторых упрощающих допущениях (азимутальная симметрия, пренебрежение радиальным распределением параметров ввиду «тонкости» электродов и др.), сводится к системе одномерных нелинейных дифференциальных уравнений второго порядка, описывающих только распределение температуры эмиттера, коллектора и разности потенциалов между электродами и их распределение по длине ЭГК. Нелинейность этих уравнений обусловлена наличием теплопередачи между электродами, излучением и эмиссионным током электронов. Во все уравнения входит зависимость эмиссионного тока от температуры эмиттера и коллектора, межэлектродного напряжения и ряда других параметров, которая и замыкает эти уравнения в единую систему. Расчет этой зависимости (локальной ВАХ ТЭП) является сложной задачей, требующей рассмотрения элементарных процессов в низкотемпературной плазме МЭЗ и процессов, протекающих на электродах ТЭП. До настоящего времени эта задача в полном объеме не решена, поэтому экспериментальное определение локальных ВАХ в ходе лабораторных стендовых испытаний ТЭП/ЭГЭ с электронагревом является актуальной задачей.

Расчет ВАХ многоэлементного ЭГК обычно сводится к последовательному расчету ВАХ входящих в него ЭГЭ и их суммированию при заданной величине протекающего электрического тока, одинакового для всех ЭГЭ вследствие их последовательного соединения. Основным блоком расчетной методики является решение системы тепловых и электрических уравнений для ЭГЭ.

Известные в литературе расчетные методики в основном позволяют выполнять оценочные и инженерные расчеты [13]. Этим методикам присущи следующие характерные особенности, существенно снижающие точность расчета:

• •    расчет ЭГК сводится к последовательному расчету входящих в его состав ЭГЭ;

• •    при построении математических моделей электротеплофизических процессов в ЭГЭ используется ряд упрощающих допущений, сильно влияющих на соответствие используемой модели реальным процессам;

• •    используемые математические модели электротеплофизических процессов в ЭГЭ в большинстве методик являются одномерными;

• •    для используемых математических моделей электротеплофизических процессов в ЭГЭ характерен некоторый произвол в выборе граничных условий.

Модернизация существующих или создание новых расчетных методик должны идти по пути частичного или полного устранения указанных выше упрощений. Сформулируем минимальный перечень требований к современным расчетным методикам:

• •    переход от одномерного к трехмерному моделированию;

• •    детальный учет зависимости свойств конструкционных материалов и сред от температуры;

• •    переход от математического моделирования процессов в ЭГЭ к ЭГК в целом;

• •    возможность проведения расчетов ЭГЭ/ЭГК сложной геометрии;

• •    возможность «сквозного» расчета для ЭГК, а в перспективе — ТРП и ЭУ в целом.

Для решения этой задачи в ГНЦ РФ–ФЭИ была выполнена модификация стандартного пакета конечноэлементного анализа COMSOL [14].

Разработанный на базе COMSOL программный комплекс COMSOL –ЭГК, оптимизированный под задачи расчета термоэмиссионных ЭГК, предоставляет пользователям полный спектр инструментов для решения поставленной задачи:

• •    построение трехмерной геометрической модели;

• •    описание физических процессов на языке математической физики;

• •    построение конечноэлементной расчетной сетки геометрической модели;

• •    расчет и постобработка результатов расчета.

Программный комплекс позволяет моделировать физические процессы электромагнетизма и сопряженного теплообмена в трехмерной геометрии как в пределах одного ЭГЭ, так и внутри коммутационного пространства ЭГК. Важным достоинством описываемого комплекса является возможность прямого использования чертежей различных ЭГК, выполненных, например, в среде автоматизированного проектирования AutoCAD.

COMSOL –ЭГК реализует методику расчета тепло- и электрофизических характеристик ЭГК и термоэмиссионной электрогенерирующей системы (ТЭС) в целом на основе трехмерной математической модели с возможностью использования в качестве исходных данных атласа экспериментальных изотермических и эквипотенциальных ВАХ ТЭП в широком диапазоне изменения таких параметров, как температура электродов, давление пара цезия и ряда других. Методика предназначена для обоснования проектных решений перспективных термоэмиссионных КЯЭУ и наземных ТЭС с ядерным или неядерным нагревом эмиттеров.

В численный алгоритм комплекса внедрены решения уравнений для электрического потенциала, генерации тока, переноса энергии тепловым излучением и электронами эмиссии, джоулева тепловыделения в электропроводящих материалах. С помощью программного комплекса COMSOL –ЭГК можно моделировать практически все физические процессы, которые описываются уравнениями в частных производных. Далее задачи решаются методом конечных элементов. Имеются также дополнительные средства для моделирования: средства для геометрических построений, генераторы сетки, инструменты постобработки и т. п.

В качестве примера для трехмерного численного моделирования с помощью программного комплекса COMSOL –ЭГК была использована базовая конструкция девятиэлементного ЭГК для термоэмиссионных КЯЭУ второго поколения (так называемый унифицированный ЭГК [15]).

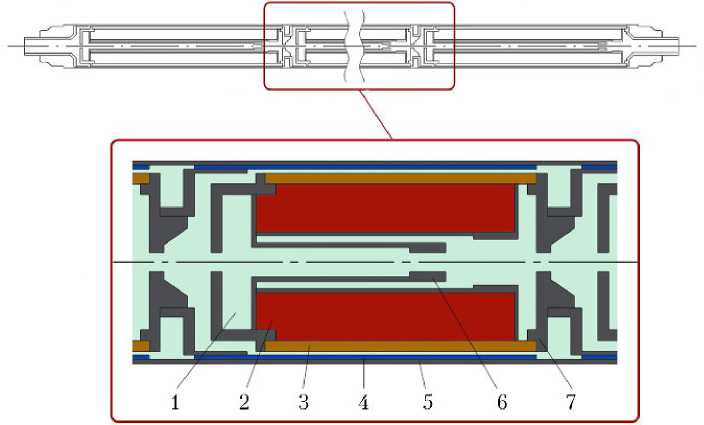
Расчетная модель ЭГК представлена на рис. 1. Эта модель многоэлементного ЭГК имеет 2 D -осесимметричное приближение. На рисунке представлен общий вид ЭГЭ/ЭГК, используемый в расчетной модели, а также более детальный вид ЭГЭ в области его межэлектродной коммутации.

Разбиение модели ЭГК на конеч- ные элементы производилось програм- мой COMSOL–ЭГК в полуавтоматическом режиме с выбором типа разбиения (квадратная или треугольная форма расчетных ячеек), а также минимального и максимального размера ячеек, кото- рый варьировался для различных сред расчетной сетки.

Основным результатом расчетов элек- тротеплофизических характеристик ЭГК с помощью программного комплекса COMSOL–ЭГК являются стационарные двумерные распределения температуры, потенциала и плотности генерируемого электрического тока. Программа также позволяет

рассчитывать

распределение

тепловых потоков в любой рассмат- риваемой области задачи, например, тепловой поток через МЭЗ. По найденным распределениям определяются такие выходные характеристики ЭГК, как изомощностная ВАХ, электрическая мощность, КПД преобразователя и ряд других.

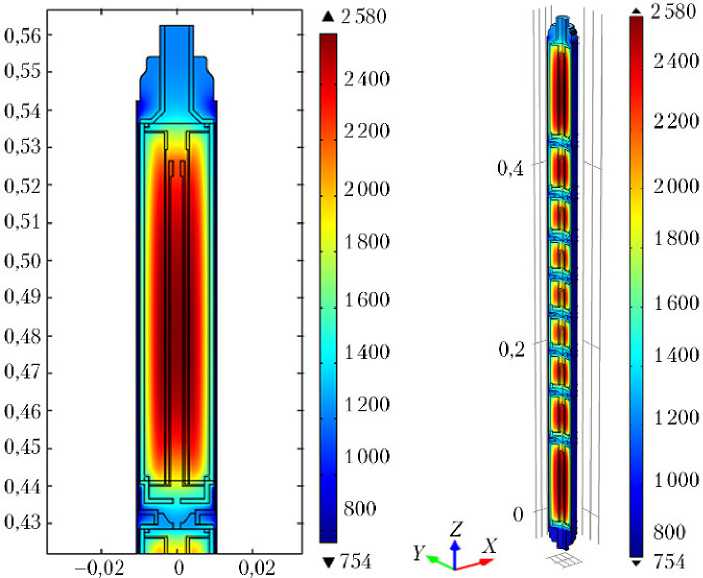
На рис. 2 представлены распределения температурного поля по конструкционным элементам отдельного термоэмиссионного ЭГЭ и девятиэлементного ЭГК в целом.

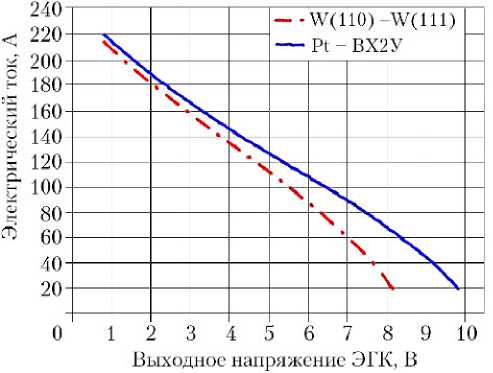
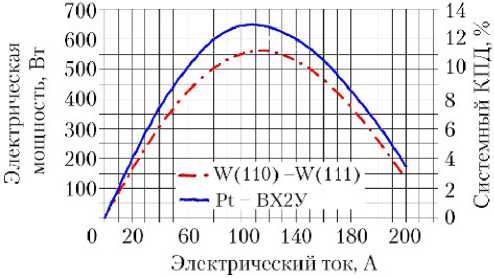
На рис. 3, а показаны

Рис. 1. Расчетная модель девятиэлементного унифицированного ЭГК, раз работанная в программной среде COMSOL–ЭГК [14]: 1 — цезиевая среда; расчетные изомощностные 2 — ядерное топливо; 3 — эмиттер; 4 — коллектор; 5 — коллекторный пакет; ВАХ ЭГК, а на рис. 3, б —

зависимости выходной

6 — газоотводящее устройство; 7 — межэлектродная коммутационная перемычка

а)                                      б)

Рис. 2. Распределение температурного поля: а — многоэлементного ЭГК —

коллекторная концевая серия при величине протекающего электрического тока 100 А (электродная пара Pt-ВХ2У [12]); б — многоэлементного ЭГК при величине протекающего электрического тока 100 А (электродная пара Pt-ВХ2У [12])

электрической мощности ЭГК от тока для различных материалов электродных пар.

Использование программного комплекса COMSOL –ЭГК для расчетов электротеплофи-зических характеристик многоэлементного термоэмиссионного ЭГК в трехмерной постановке показало достаточную гибкость и эффективность этой методики, позволяющей во всей полноте учесть реальную конструкцию ЭГК и разнообразие физических свойств материалов его конструктивных элементов.

Моделирование тепловых и электрических характеристик многоэлементного ЭГК с помощью программного комплекса COMSOL –ЭГК открывает путь к полноценному исследованию

термомеханических напряженно-деформированных состояний конструкционных элементов и сред ЭГК в трехмерной постановке, что является одной из приоритетных задач при обосновании ресурсных характеристик ЭГК и термоэмиссионной ЯЭУ в целом. Использование программного комплекса COMSOL –ЭГК может сыграть важную роль в разработке методов прогнозирования ресурса термоэмиссионных ЭГК по результатам его петлевых реакторных испытаний на укороченной временной базе.

б)

Рис. 3. Изомощностные эквипотанциальные ВАХ ЭГК для различных материалов электродных пар (а) и зависимость выходной электрической мощности ЭГК от тока для различных материалов электродных пар (б) [14]

методы нейтронно-физического расчета и оптимизации активной зоны термоэмиссионного реактора-преобразователя

В связи со спецификой применения термоэмиссионных ЯЭУ на них накладываются ограничения, прежде всего — по массогабаритным параметрам.

Следовательно, задача нейтроннофизического расчета — выбрать такую конфигурацию активной зоны, которая удовлетворяла бы поставленным условиям по тепловой мощности, запасу реактивности, обеспечению безопасной эксплуатации, а с другой стороны, имела бы минимально возможные габариты и массу. Такая задача является, по сути, оптимизационной и может быть решена с применением соответствующих математических методов.

Расчет нейтронно-физических характеристик ТРП изначально проводился по одномерным программам в рамках теории возмущений, вариационного исчисления и др. [16]. В гомогенной модели невозможно было учесть многие особенности малогабаритных реакторов. В частности, не было возможности точно моделировать располагающиеся в отражателе поворотные цилиндры регулирования реактивности. Расчеты проверялись экспериментально на физических стендах [17]. Основываясь на данных экспериментов, для оптимизации эффективного коэффициента размножения нейтронов ( K _эфф ) определялась функция эффективности топлива, которая показывала, насколько изменяется K _эфф реактора при перераспределении топлива по объему активной зоны. Функция эффективности топлива определялась дифференцированием кривой зависимости K _эфф от положения топлива в активной зоне [18].

С развитием вычислительных машин и методов расчета ядерных реакторов более широко стали применяться алгоритмы, основанные на использовании ММК. Применяемые в ГНЦ РФ–ФЭИ современные расчетные программные комплексы, основанные на ММК, такие как MMKFK -2 [19] и MCNP [20], позволяют детально воспроизводить компоновку активной зоны термоэмиссионного реактора, в состав которого также входят торцевой и боковой отражатели, поворотные органы регулирования, коллекторы теплоносителя. При моделировании учитывается изотопный состав материалов конструкционных элементов, положение органов регулирования, наполненность каналов теплоносителем и др. Пример расчетной модели реактора «ТОПАЗ», построенной в программном комплексе MCNP , показан на рис. 4.

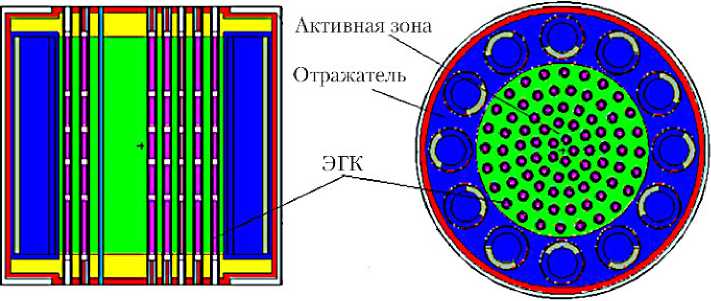
Рис. 4. Расчетная модель ТРП «ТОПАЗ», построенная в программном комплексе MCNP

Также достаточно детально учитываются особенности конструкции ЭГК. В состав расчетной модели ЭГК входят ядерное топливо, эмиттер, слои коллекторного пакета, система отвода газообразных продуктов деления, коммутационные перемычки между отдельными ЭГЭ, торцевые отражатели нейтронов и т. д. В некоторых случаях для ускорения счета коммутационные перемычки представляют в виде гомогенной смеси. На рис. 5 представлен фрагмент характерной расчетной модели такого ЭГК.

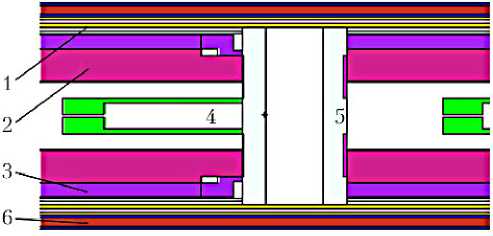
Рис. 5. Фрагмент расчетной модели ЭГК, построенной в программном комплексе MCNP: 1 — коллекторный пакет; 2 — топливо; 3 — эмиттер; 4 — система отвода газоподобных продуктов деления; 5 – коммутация; 6 — тракт теплоносителя

Такое детальное представление ЭГК необходимо, в т. ч., и для получения распределения тепловыделения по высоте и диаметру твэл, которое необходимо для электротеплофизического расчета ЭГК (см. выше).

Расчет реактора подразумевает изменение множества параметров, поэтому подбор компоновки активной зоны, толщины отражателя и др. параметров для удовлетворения поставленным условиям является сложной задачей.

Наряду с развитием вычислительных методов появились новые методики оптимизации. Одним из таких методов является генетический алгоритм (ГА) — адаптивный метод поиска, основанный на механизмах и методах эволюции и генетических процессах. Подбор вариантов решений проходит с помощью математических формул, описывающих такие природные механизмы, как скрещивание и мутации, на которые, в свою очередь, влияет окружающая среда [21].

Важной особенностью ГА является то, что он не требует явного задания оптимизируемой функции и способен работать напрямую с численными решениями уравнения переноса, получаемыми из расчетной программы (например, из расчетов ММК).

Удачным подходом стало соединение комплекса для расчета реактора и оптимизационной методики, оперирующей непосредственно размерами конструктивных элементов активной зоны и реакторными функционалами, получаемыми при расчете реактора.

На основе данных, заданных пользователем, разработанная программа подготавливает набор начальных точек, далее, после применения операторов ГА, количество вариантов решений увеличивается в несколько раз. Затем программа автоматически запускает расчет всех этих вариантов с применением расчетного комплекса. По результатам расчета проводится оценка удовлетворения поставленным условиям и делается вывод о выполнении поставленной задачи. Генетический алгоритм применяется для анализа полученной в результате расчетов реактора информации и выработки на основе этого анализа рекомендаций по изменению параметров конструкции.

При разработке термоэмиссионного реактора-преобразователя важной задачей является снижение коэффициента неравномерности энерговыделения по радиусу активной зоны ( K_r ), так как высокий K_r влияет на значение характеристики ЭГК, что негативно отражается на способности реактора-преобразователя обеспечивать необходимую электрическую мощность [22].

ЭГК в ТРП располагаются, как правило, по концентрическим окружностям.

От их расположения зависит запас реактивности реактора и энерговыделение в каждом ЭГК. При этом, как показы- вают результаты расчетов, уменьшение радиального коэффициента неравномерности энерговыделения приводит к снижению запаса реактивности реактора, т. е. задача состоит в том, чтобы найти такое расположение ЭГК, при котором коэффициент неравномерности будет низким, а запас реактивности достаточным.

При моделировании активной зоны положение ЭГК задается двумя координатами. Эти координаты рассчитываются из значения радиуса окружности расположения ЭГК и их количества на отдельной окружности. Таким образом, оптимизационными параметрами становятся значения радиусов окружностей расположения ЭГК и количество ЭГК на каждой из окружностей. Также параметры могут быть дополнены, например, радиусом активной зоны, величиной обогащения топлива, углом поворота окружностей относительно друг друга.

На все параметры могут быть нало- жены ограничения, например, минимально возможное расстояние между ЭГК соседних окружностей, минимальное соотношение радиуса активной зоны и радиуса периферийной окружности расположения ЭГК и др.

Таким образом, решаемую оптими- зационную задачу можно представить в следующим виде: Kэфф→max K ≤ K или

r min

– R_i ≥ d

r

^R i +1

где   Krmin   и Kэффmin значение коэффициента

K_r → min K эфф ≥ K эффmin R_{i +1} – R_i ≥ d , минимальное

неравномерности

энерговыделения по радиусу реактора и минимально допустимое значение коэффициента размножения нейтронов, соответственно; Ri — значение радиуса окружности расположения ЭГК; d — минимально допустимое расстояние между ЭГК.

Результатами работы программы являются численные значения параметров, отвечающих за такую компоновку активной зоны реактора, расчетные значения функционалов которой отвечают поставленным требованиям.

Важным практическим результатом стало то, что для различных ТРП космического назначения удалось получить снижение радиального коэффициента неравномерности энерговыделения с 1,30 до 1,09 [23], что приводит к увеличению генерируемой электрической мощности, при этом запаса реактивности достаточно для полной кампании. Распределение относительной тепловой мощности ЭГК в исходном и оптимизированном вариантах компоновки активной зоны ТРП показано на рис. 6.

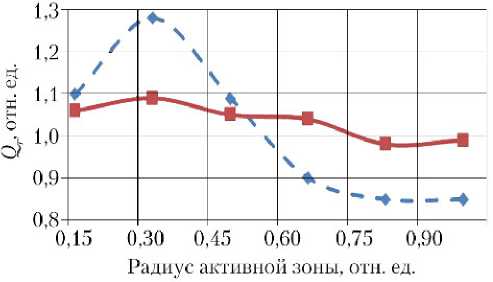
Рис. 6. Распределение относительной мощности ЭГК:

♦ — исходный вариант; ■ — оптимизированный вариант

Применяемый подход позволяет наиболее полно исследовать оптимизационное пространство, а значит, получать наилучшие из возможных решений, что особенно важно для малогабаритных термоэмиссионных ЯЭУ.

методы нейтронно-физического расчета и оптимизации теневой радиационной защиты термоэмиссионного ядерного реактора-преобразователя

В общем контексте проектирования КЯЭУ радиационная защита занимает особое место, так как в ряде случаев именно ее габариты и масса определяют принципиальную возможность реализации проекта в рамках наложенных ограничений.

Определение габаритов радиационной защиты — это оптимизационная задача, так как с одной стороны необходимо обеспечить определенный уровень излучений за защитой, а с другой — ее минимально возможные габариты и массу.

Первоначально при оптимизации применялись методы, требующие наличия явного вида уравнения целевой функции, такие как, например, градиентные методы или методы множителей Лагранжа. При этом описание процессов проводилось с помощью сложных систем многогрупповых уравнений. Все это требовало внесения упрощений — ослабление излучения описывалось через экспоненциальное приближение; вторичное γ-излучение, вызванное радиационным захватом нейтронов в материалах радиационной защиты, не учитывалось; слои защиты рассматривались целыми, не имеющими каких-либо неоднородностей [24].

С появлением расчетных программных комплексов, основанных на ММК, стало возможным подробное описание радиационной защиты ТРП. В качестве примера на рис. 7 представлена такая трехмерная модель.

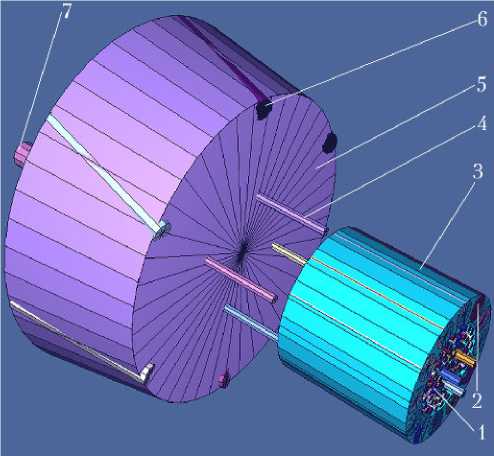
Рис. 7. Трехмерная модель реактора и радиационной защиты, построенная в программном комплексе MCNP: 1 — активная зона; 2 — орган регулирования; 3 — боковой отражатель; 4 — рессора привода органов регулирования; 5 — теневая радиационная защита; 6 — труба с теплоносителем; 7 — привод органов регулирования

В модели учитываются проникающие элементы, такие как трубы с теплоносителем, приводы органов регулирования. Кроме того, радиационная защита разбита на тяжелый, ослабляющий поток γ-излучения, и легкий — ослабляющий поток нейтронов, компоненты.

Особенностью применяемого подхода является то, что для расчета реактора и радиационной защиты применяется один и тот же комплекс. Расчет радиационной защиты происходит при полноценной, без каких-либо упрощений или изменений, конечной модели реактора, что позволяет учесть множество тонких факторов и избежать гомогенизации элементов ядерной энергетической установки, вносящей неопределенности в получаемые значения радиационных функционалов [25].

Кроме того, разработан подход, позволяющий значительно снизить время расчета одного варианта компоновки радиационной защиты. Метод последовательных расчетов с весовыми окнами позволяет ускорить сходимость результатов в десятки и сотни раз.

Суть метода состоит в разделении всего объема расчетной модели регулярной независимой сеткой, для всех ячеек которой программным образом рассчитываются функции ценности, являющиеся весовыми окнами для каждой последующей итерации расчета переноса частиц.

Неполнота статистики компенсируется использованием среднего значения потоков в соседних ячейках, пренебрегая ослаблением в областях с плохой статистикой и тем самым практически гарантируя заниженную оценку ценности и устойчивость счета [26].

Детальное моделирование радиационной защиты позволяет создать методику ее оптимизации, основанную на физическом смысле тока контрибутонов [27]. Помещая поверхность S в любом месте между ядерным реактором и защищаемым объектом, можно определить значение функционала радиационной нагрузки на защищаемом объекте, а также вклад в него элемента поверхности S , что и является током контрибутонов [28].

Если в качестве поверхности S выбрать поверхность слоя радиационной защиты и покрыть ее «черным телом», имеющим кольцевой вырез, как это показано на рис. 8, в защищаемые объекты будут попадать только частицы из кольцевой зоны поверхности радиационной защиты, над которой этот вырез расположен.

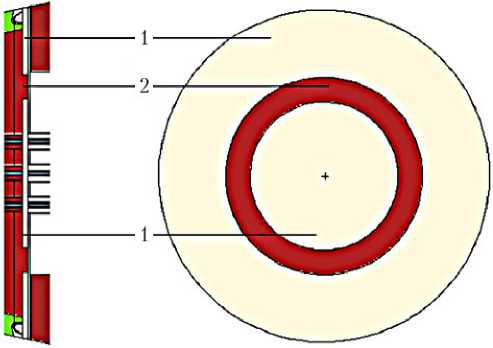
Рис. 8. Схема расчета тока контрибутонов с поверхности непрофилированного слоя: 1 — «черное тело»; 2 — кольцевая зона профилируемого слоя радиационной защиты

А значения радиационных нагрузок на них равны вкладу данной зоны в результат, получаемый со всей поверхности. Далее, смещая положение кольцевой зоны так, чтобы внутренний радиус выреза на следующем шаге равнялся внешнему, всю поверхность профилируемого слоя радиационной защиты разбивают на центральную окружность и кольцевые зоны, от которых вычисляется их индивидуальный вклад в дозу или флюенс на каждом из защищаемых объектов.

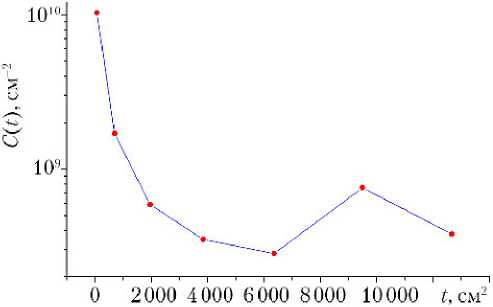
Полученные величины дозовых нагрузок для каждого положения кольцевого выреза интерполируются, полученная функция является распределением тока контрибутонов по поверхности радиационной защиты. Распределение тока контрибутонов С ( ^→ r ), рассчитанное для одного из защищаемых объектов, приведено на рис. 9, а . Далее с использованием методов теории оптимального управления определяется профиль слоя радиационной защиты. Полученный таким образом профиль радиационной защиты обеспечивает допустимые дозовые нагрузки на защищаемых объектах (рис. 9, б ).

Высокие значения вкладов в центре радиационной защиты связаны, в первую очередь, с наличием в защите проникающих конструкций, через которые происходит повышенная утечка излучений, а во вторую — с близостью этой зоны к оси симметрии ЯЭУ, на которой расположен защищаемый объект. Другое увеличение удельного вклада связано с утечками через трубы с теплоносителем.

Другим подходом к оптимизации характеристик радиационной защиты, разработанным в АО «ГНЦ РФ–ФЭИ», является, как и в случае оптимизации активной зоны (см. выше), соединение расчетного комплекса с оптимизационной методикой [29].

Этот подход позволяет максимально точно учитывать влияние на перенос излучения многочисленных неоднородностей в радиационной защите, а также влияние элементов космического аппарата, расположенных за защитой. Кроме того, данная методика не требует какого-либо аналитического описания зависимости целевой функции от варьируемых параметров. Как следствие, она исключает модельную погрешность, а также погрешность результатов косвенных расчетов, вызванную математическими операциями над величинами, определенными с погрешностью.

В качестве ограничений в данной задаче при поиске минимума массы защиты могут быть заданы допустимые потоки нейтронов и γ-частиц на защищаемом объекте. В случае поиска минимальных уровней потоков нейтронов и γ-квантов максимально допустимая масса защиты может быть задана в качестве ограничения.

а)

б)

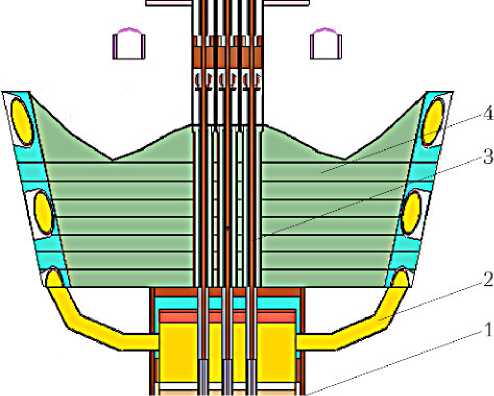
Рис. 9. Результат расчета профиля радиационной защиты: а — пример рассчитанного распределения тока контрибутонов по поверхности слоя радиационной защиты как функция площади поверхности слоя; б — полученный профиль радиационной защиты (1 — реактор; 2 — труба с теплоносителем; 3 — приводы органов регулирования; 4 — теневая радиационная защита)

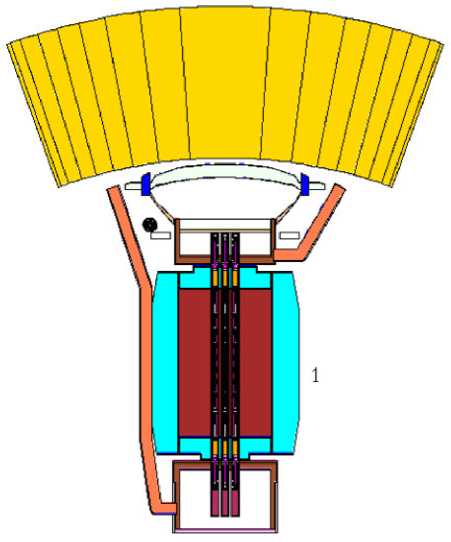
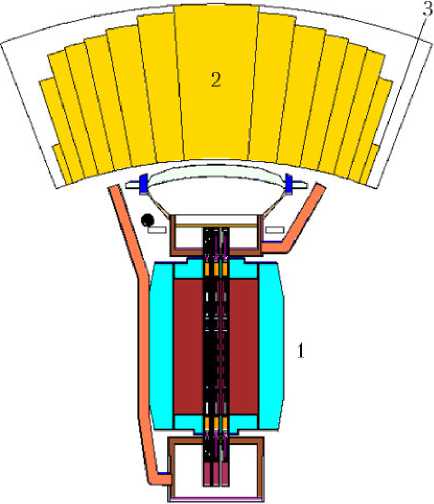
На рис. 10 представлены результаты работы программы для задачи оптимизации профиля и толщины легкой радиационной защиты ТРП при наличии крупногабаритного рассеивателя. При оптимизации конус радиационной защиты разбивается на блоки. Высоты каждого блока являются параметрами оптимизации и варьируются независимо друг от друга. Также в качестве параметра оптимизации выбран угол тени радиационной защиты. В результате расчетов удалось снизить массу радиационной защиты на величину не менее 40 кг.

Полученные результаты свидетельствуют о хорошей применимости разработанных алгоритмов и компьютерных комплексов к задачам оптимизации радиационной защиты и возможности осуществления с их помощью оптимального поиска в автоматическом режиме.

а)

б)

Рис. 10. Результаты работы методики оптимизации [23]: а — 0 итерация, М = 160 кг; б — найденное решение, М = 118 кг; 1 — реактор; 2 — теневая радиационная защита; 3 — угол тени

Применение разработанной методики позволяет добиться снижения массы радиационной защиты уже после нахождения ее оптимальной компоновки и учесть требования к допустимым радиационным нагрузкам одновременно нескольких защищаемых объектов.

заключение

На протяжении более 60 лет в АО «ГНЦ РФ–ФЭИ» накапливаются компетенции в области процессов термоэмиссионного преобразования тепловой энергии в электричество, в физике активной зоны малогабаритных реакторов, прохождении излучения через вещество. Все эти знания в соединении с современными расчетными комплексами и новыми математическими методами позволяют проводить физико-техническое обоснование характеристик при разработке и эксплуатации инновационных КЯЭУ с прямым преобразованием тепловой энергии в электричество. Описанные методы расчетного обоснования характеристик КЯЭУ, несомненно, будут востребованы для решения новых задач, появившихся со вступлением мировой космической индустрии в эру, названную в литературе Космос 2.0 [30].