Обзор современных методов планирования движения
Автор: Казаков К.А., Семенов В.А.
Журнал: Труды Института системного программирования РАН @trudy-isp-ran
Статья в выпуске: 4 т.28, 2016 года.
Бесплатный доступ
Автоматизация технологически сложных процессов в машиностроении, энергетике, транспорте, медицине, строительстве, а также создание новых продуктов и сервисов невозможны без решения задач планирования движения. В последнее время интерес к ним заметно возрос в связи с развитием средств компьютерного моделирования и становлением таких дисциплин как комплексное планирование индустриальных программ, реалистичная анимация трехмерных сцен, роботизированная хирургия, навигация в динамическом окружении, автоматическая сборка продуктов, организация транспортных потоков в мегаполисах. Данная работа посвящена обзору и сравнительному анализу современных математических методов планирования движения.
Планирование движения, поиск пути, маршрутные сети, определение столкновений
Короткий адрес: https://sciup.org/14916373
IDR: 14916373 | DOI: 10.15514/ISPRAS-2016-28(4)-14
Текст научной статьи Обзор современных методов планирования движения
Автоматизация технологически сложных процессов в машиностроении, энергетике, транспорте, медицине, строительстве, а также создание новых продуктов и сервисов невозможны без решения задач планирования движения. В последнее время интерес к ним заметно возрос в связи с развитием средств компьютерного моделирования и становлением таких дисциплин как комплексное планирование индустриальных программ, реалистичная анимация трехмерных сцен, роботизированная хирургия, навигация в динамическом окружении, автоматическая сборка продуктов, организация транспортных потоков в мегаполисах. Данная работа посвящена обзору и сравнительному анализу современных математических моделей, методов и программных средств планирования движения [1].
Обычно под планированием движения понимается поиск бесконфликтного пути для перемещения твердого тела или кинематической конструкции в пространственно-трехмерной сцене. Искомый путь представляет собой непрерывную кривую в конфигурационном пространстве объекта, которая соединяет его начальное и конечное положения, исключает столкновения с препятствиями сцены и удовлетворяет всем установленным кинематическим и динамическим ограничениям.
Пусть задана сцена как непустое множество препятствий 0 с W в области эвклидова пространства W с EN, N е {2,3}. Пусть также задано твердое тело А с W либо кинематическая цепь А{В,]}, где В = {бп В2, ■■■,Sn} с W - множество твердотельных звеньев, a J — Ui>Ji> ■■■ >1к^ - множество кинематических ограничений таких, что при корректной конфигурации цепи предикаты ограничений /і(с),/2(с),... ,/к(с) принимают истинное значение. Под конфигурацией с е Сл здесь понимается набор значений параметров, однозначно определяющий положение точек объекта А в пространстве сцены. Обычно используется минимальный набор параметров, соответствующий количеству степеней свободы объекта и определяющий пространство состояний или конфигурационное пространство объекта СА.
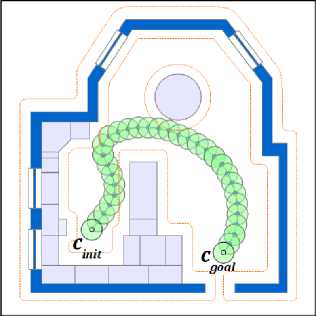
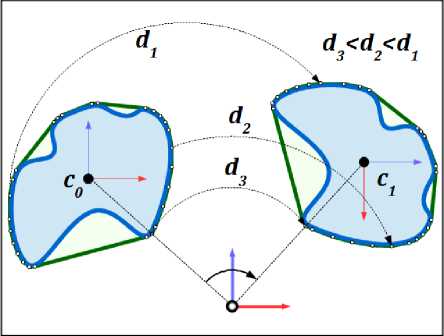
Рис. 1. Конфигурационное пространства двумерного твердого тела
Fig. 1. Configuration space of two dimensional solid body
(Ь)
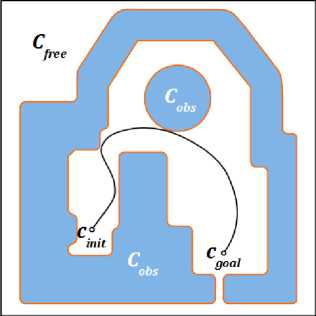
Определение. Пространством допустимых состояний назовем множество всех конфигураций объекта с е Сд, удовлетворяющих кинематическим ограничениям и исключающих столкновения с препятствиями сцены С^тее = {с е Сд |/і(с)Д/2(с), ...,A/k(c) ДВДс) n 0 = 0, ...,ДВп(с) n 0 = 0 }. Для простого твердого тела свободное множество определяется как Qree = {сеСл|А(с)пО = 0}.
Тогда постановка задачи поиска пути может быть сформулирована следующим образом. Для пары заданных бесконфликтных конфигураций С/П££, cgoai е Сутее требуется найти непрерывный путь р(т): [0,1] -» CfTee такой, что р(0) = Сіпк и Р(1) — Сдоа.1-
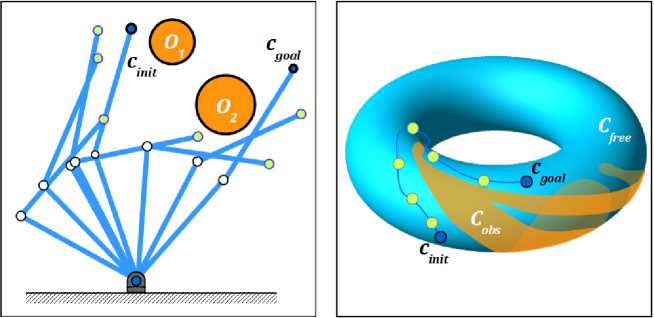
(а) (Ь)
Рис. 2. Конфигурационное пространства двухзвенного манипуляционного робота
Fig. 2. Configuration space of 2-DOF manipulation robot
Поскольку планирование маршрута, как правило, допускает бесконечное множество решений (хотя может не существовать ни одного решения), иногда данную задачу формулируют в постановке оптимизационной задачи с целевой функцией, соответствующей минимальной длине маршрута или максимальной удаленности перемещаемого объекта от препятствий [2,3].
На практике поиск пути даже в простых сценах с относительно небольшим количеством препятствий становится трудноразрешимой задачей, если перемещаемый объект имеет сложную геометрию или высокое число степеней свободы. В современных индустриальных приложениях часто требуется моделировать поведение сложных кинематических систем с шестью и более степенями свободы в статическом или динамическом окружении, насчитывающим тысячи препятствий.
Функционал существующих прикладных программных пакетов, таких как Kineo САМ (Kineo Computer Aided Motion) [4], ROS (Robot Operating System)
[5], OMPL (Open Motion Planning Library) [6], OpenRAVE (The Open Robotics Automation Virtual Environment) [7] и CuikSuite [8] главным образом обеспечивает решение задач моделирования неголономных механических систем в режиме реального времени и локального планирования движения. Математический арсенал упомянутых пакетов в основном ограничен сэмплинг-методами, которые эффективны в приложениях, связанных, в частности, с управлением движением промышленных роботов при сборке компонентов, программированием координатно-измерительных машин при контроле точности производимых изделий. Однако данные методы демонстрируют несостоятельность в тех случаях, когда требуется определение протяженных бесконфликтных траекторий в трехмерном окружении со сложной топологией. Подобные задачи возникают, например, при пространственно-временной верификации календарно-сетевых графиков архитектурно-строительных проектов и нуждаются в более развитом математическом аппарате [9-11]. При этом архитектура программных пакетов и особенности организации интерфейсов препятствуют реализации в их составе новых глобальных методов планирования движения и интеграции в индустриальные системы, ориентированные на работу с масштабными сценами, состоящими из сотен тысяч и миллионов объектов с индивидуальными геометрическими и динамическими характеристиками.
Таким образом, разработка эффективных математических методов и программных средств планирования движения представляет собой актуальную научную проблему. Настоящая статья посвящена систематическому обзору и сравнительному анализу современных математических методов планирования движения. Важное внимание уделяется ключевым подходам, основанным на пространственной декомпозиции, маршрутных сетях и физических аналогиях с потенциальными полями. Предполагается, что обзор поможет в выработке общих рекомендаций по использованию методов, а также в их выборе при решении практических классов задач. Ожидается также, что обзор послужит конструктивной основой для концептуализации теории планирования движения и создания единой программно-инструментальной среды разработки приложений.
-
2. Методы на основе пространственной декомпозиции
-
2.1 Регулярная декомпозиция
Наиболее простой и в то же время распространенный подход к планированию движения состоит в применении методов пространственной декомпозиции. Он предполагает разбиение свободных областей сцены на множество простых регионов с использованием тех или иных методов декомпозиции, определение смежности регионов и формирование графа связности, который в дальнейшем может использоваться для навигации в сцене. Фактически, подход реализует схему редукции вычислительно сложной задачи планирования движения в эвклидовом пространстве к типовой задаче поиска пути в графе.
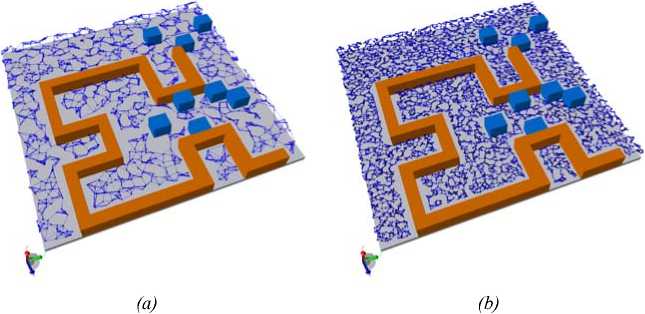
Одним из способов реализации данного подхода является применение методов регулярной пространственной декомпозиции. Данные методы предполагают разбиение всего объема сцены сеткой с фиксированным размером ячеек, ориентированных по осям координат (рис. 3, а). Для всех ячеек определяется статус занятости. Ячейки могут быть целиком заполненными объектами сцены, частично заполненными или свободными. Маршрут строится путем анализа смежных свободных ячеек, выбора направлений для распространения и проверки принадлежности перемещаемого объекта свободным ячейкам сетки. Таким образом, вместо исходной точной геометрической модели сцены используется ее упрощенное дискретное представление, что существенно упрощает процесс маршрутизации. Вопросы использования методов регулярной декомпозиции применительно к планированию движения широко освещены в литературе [12,13].
Метод относительно прост в реализации, однако требует значительных вычислительных ресурсов из-за необходимости детальной дискретизации всего пространства сцены и обеспечения приемлемой точности маршрута.
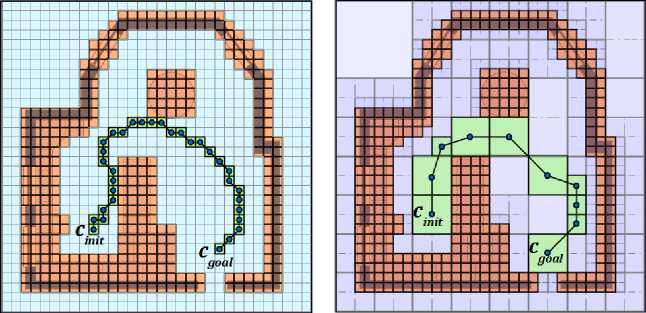
(а) (Ь)
Рис. 3. Пример построения декомпозиции двумерной сцены с помощью (а) равномерной сетки и (Ь) дерева квадрантов
Fig. 3. An example of decomposition of 2D scene using (a) regular grid and (b) quad tree
Указанного недостатка лишены методы регулярной адаптивной декомпозиции пространства, одним из известных представителей которых является метод на основе октодеревьев занятости [10,14,15]. Благодаря рекурсивной процедуре декомпозиции такие структуры оказываются более экономичными (рис. 3, Ь). Если принимать во внимание возможную неравномерность распределения объектов по объему сцены и существенную вариацию их размеров, октарные структуры оказываются более рациональными при дискретизации сцены и исполнении типовых запросов, связанных с пространственной локализацией объектов, поиском соседей, определением столкновений. Однако процедура маршрутизации становится более сложной, а с учетом несбалансированности октодеревьев может приводить и к неестественным траекториям, содержащим большое число изломов. Для преодоления этой проблемы был предложен гибридный метод, использующий окаймление на границах ячеек [16]. Однако он вряд ли может рассматриваться в качестве универсального, поскольку неизбежно порождает избыточное представление сцены и требует существенных дополнительных расходов.
-
2.2 Объектно-зависимая декомпозиция
-
3. Методы на основе маршрутных сетей
Альтернативу методам пространственной декомпозиции составляют методы объектно-зависимой декомпозиции пространства. За счет выделения свободных областей непосредственно по границам объектов сцены устраняются проблемы, обусловленные погрешностью дискретизации сцены. К сожалению, методы этого семейства обладают высокой вычислительной сложностью и в большинстве случаев не могут конкурировать с методами пространственной декомпозиции. Наиболее известными методами объектнозависимой декомпозиции являются метод вертикального разбиения или трапецеидальной декомпозиции (Trapezoidal Decomposition) [17], триангулированное разбиение [18], цилиндрическая декомпозиция (Cylindrical decomposition) [19], а также декомпозиция Морса [1,20].
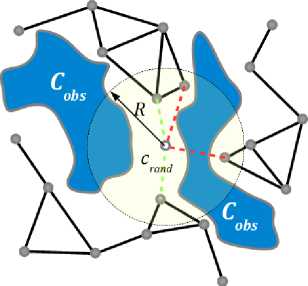
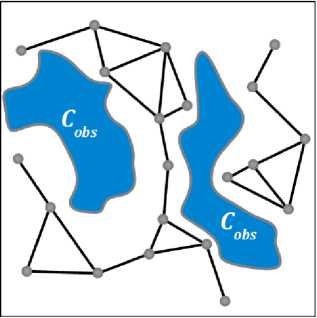
Важное семейство методов глобального планирования движения составляют методы на основе маршрутных сетей, которые обычно строятся в конфигурационном пространстве перемещаемого объекта или в пространстве сцены. Подобные сети объединяют в себе бесконфликтные переходы или участки путей и расширяются по мере совершения новых успешных попыток перемещения. Иногда сети накапливают также информацию о предпринятых неудачных попытках и связанных с ними вычислительных затратах, что позволяет в дальнейшем выбирать более перспективные направления и ускорить процесс маршрутизации при решении как одиночных, так и множественных задач планирования движения.
Формально маршрутная сеть представляет собой топологический граф G(V, Е), вершины V которого соответствуют бесконфликтным конфигурациям перемещаемого объекта S с Cfree, а ребра Е - бесконфликтным переходам между ними Р(т): [ОД] -» С^тее, Р(0) с S, Р(1) с S. Обычно маршрутная сеть строится в предположении выполнения условий достижимости и связности.
Определение. Маршрутная сеть достижима для конфигурационного пространства объекта, если для любой его точки с е С^тее существует вершина маршрутной сети 5 6 5 и бесконфликтный путь к ней р(т): [0,1] -» Cfree, р(0) = с и р(1) = 5.
Определение. Маршрутная сеть объекта связна для конфигурационного пространства объекта, если для любой его пары точек Сіпк, cgoal е Qree, между которыми существует бесконфликтный путь и найдены сопряженные вершины маршрутной сети s£n£t,ssonZе 8, также существует маршрут рХт): [ОД] -»5, где р'(0) = с/п/£ и р'(1) = сдоа1.
Данные условия обеспечивают гарантированное нахождение бесконфликтного маршрута между любыми двумя положениями объекта при условии, что он существует. Первое условие позволяет соединить любую пару заданных точек свободного пространства с маршрутной сетью. Второе условие обеспечивает навигацию по маршрутной сети. К сожалению, данные условия носят декларативный характер и не могут быть конструктивно применены при разработке и реализации методов планирования движения.
Однако сама идея маршрутной сети достаточно плодотворна и нашла воплощение в ряде методов, прежде всего в методах PRM и RRT, подробно обсуждаемых в следующих разделах. Маршрутные сети, развернутые непосредственно в пространстве сцены, предоставляют дополнительные возможности для решения задач планирования движения с разными объектами. Однако в этом случае переходы, бесконфликтные для одного перемещаемого объекта, могут оказаться конфликтными для других объектов. Поэтому построенные маршруты нуждаются в дополнительной верификации, а сама сеть - в достоверных методах анализа переходов для маршрутизации новых объектов.
-
3.1 Графы видимости
-
3.2 Диаграммы Вороного
Один из известных методов организации маршрутных сетей основан на применении графов видимости (Visibility Graphs) [18]. В простейших случаях граф видимости строится на множестве вершин полигонов или полиэдров, являющихся геометрическими моделями препятствий сцены, и дополняется начальными и конечными точками маршрутов. Все вершины попарно соединяются линейными отрезками, которые принимаются в качестве ребер графа при условии попарной “видимости” инцидентных им вершин и отсутствия пересечения с препятствиями сцены (рис. 4, а). Сложность построения графа видимости для сцены, представленной полигонами с общим числом вершин п, составляет O(ri2log ri) [1], что является довольно затратным для применения в индустриальных приложениях.
Кроме того, преобразование топологического графа в маршрутную сеть также представляет собой сложную задачу, поскольку ребра графа видимости проходят точно через вершины препятствий, и для успешной навигации требуется коррекция путей или предварительное расширение границ препятствий. Избыточное количество порождаемых маршрутов, крайне нежелательное при моделировании сложных сцен, также является недостатком данного метода. Тем не менее, в двумерном окружении с относительно небольшим числом препятствий данный метод может успешно применяться, например, для решения задач поиска кратчайшего пути в сцене. Более того, существуют попытки использования графов видимости для планирования движения в динамическом окружении [21,22].
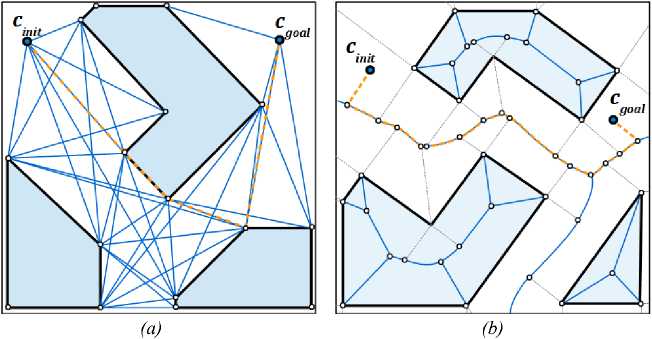
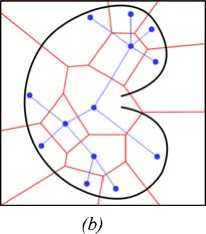
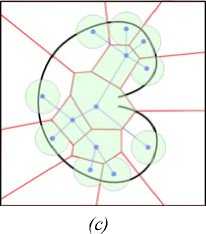
Рис. 4. Пример построения (а) графа видимости и (Ь) диаграммы Вороного в двумерной полигональной сцене
Fig. 4. An example of (a) visibility graph and (b) Voronoi diagram in two dimensional polygon scene
Альтернативный метод определения маршрутов основан на использовании обобщенных диаграмм Вороного (Generalized Voronoi Diagrams) [1]. Наиболее привлекательное свойство диаграммы Вороного заключается в том, что она является деформационным ретрактом свободного пространства. Тем самым, любой бесконфликтный путь может быть непрерывно отображен в диаграмму Вороного. Более того, метод обеспечивает наибольшее удаление от границ препятствий при условии, что движение осуществляется вдоль ребер диаграммы. Данное свойство позволяет определять наиболее “безопасные” маршруты перемещения в сцене (рис. 4, Ь).
Наивная реализация данного метода обладает высокой вычислительной сложностью 0 (и)4, где п - общее количество вершин и граней препятствий [23]. Известны эффективные алгоритмы с лучшими асимптотическими оценками сложности, однако они неустойчивы к вырожденным случаям и трудны для надежной реализации.
Диаграмма Вороного определяется для произвольного метрического пространства. Несмотря на это, ее применение для навигации в эвклидовых пространствах размерности выше двух является затруднительным ввиду того, что маршрутная сеть уже не представляет топологически одномерную структуру. В этих случаях обычно применяются методы на основе обобщенных диаграмм Вороного [24].
-
4. Дискретный поиск
-
4.1 Неинформированный поиск
-
4.2 Эвристический поиск
Методы на основе пространственной декомпозиции и маршрутных сетей позволяют редуцировать вычислительно трудные задачи навигации в сложном многомерном окружении к более простым задачам теории графов, для решения которых имеется развитый математический аппарат. Тем не менее, задачи планирования движения привносят свои особенности в постановку и решение подобных задач [25-27].
Например, маршрутные сети не только представляют топологию свободных областей сцены, но и часто накапливают дополнительную информацию для выбора более достоверных и оптимальных маршрутов навигации. Такими данными могут быть, например, протяженность переходов в маршрутной сети, расстояние до ближайших препятствий сцены, информация о предпринятых удачных и неудачных попытках расширения сети и затраченных для этого вычислительных ресурсах. Подобные данные позволяют использовать эвристические оценки рисков и перспективности маршрутов и, тем самым, ускорить решение одиночных и множественных задач маршрутизации.
Классические алгоритмы теории графов реализуют поиск в ширину, поиск в глубину, поиск по критерию стоимости [25]. Данные алгоритмы предполагают полный обход вершин графа без какой-либо информации о том, насколько каждый шаг приближает процесс поиска к решению. Применение данных алгоритмов сопряжено со значительными вычислительными затратами, и поэтому они редко применяются при решении задач планирования движения.
Эвристические алгоритмы поиска пути предназначены для быстрого отыскания маршрута в графе путем распространения в направлении более перспективных вершин. Для этого обычно организуется очередь из непосещенных вершин, порядок в которой определяется на основе эвристических правил приоритизации.
Одним из наиболее популярных алгоритмов поиска пути данного семейства является А* [28]. Приоритет вершины в данном алгоритме определяется суммой: /(v) = gCv) + /i(v), где ^(v) - стоимость пути из начальной вершины в данную, a /i(v) - эвристическая оценка стоимости пути до целевой вершины.
При этом значение h(v) должно быть неотрицательным и удовлетворять неравенству треугольника. Таким образом, А* является обобщением алгоритма Дейкстры при /(v) = 5 (v) и алгоритма жадного поиска при/(v) = /i(v).
Использование эвристики, как правило, позволяет значительно уменьшить количество посещаемых вершин и, как следствие, повысить производительность поиска. Кроме того, алгоритм находит оптимальные решения при условии, что эвристическая оценка является оптимистической, т.е. значение функции h(v) всегда меньше либо равно точной стоимости пути до целевой вершины.
В наихудшем случае выполнение алгоритма А* может быть сопряжено с экспоненциальным ростом числа непосещенных вершин в очереди, что при большом коэффициенте ветвления дерева поиска порождает проблему чрезмерного потребления памяти. В таких случаях более предпочтительным является использование алгоритма А* с итеративным углублением ( Iterative Deeping А* ) [29] или алгоритма А* с ограничением памяти (Memory Bounded А*) [30].
-
4.3 Поиск в регулярной сетке
-
4.4 Алгоритм Lifelong Planning А*
Методы пространственной декомпозиции на основе регулярных равномерных сеток приводят к дискретному представлению сцены в виде графов с большим количеством вершин и неопределенностью в их приоритизации из-за равной стоимости переходов. Одним из способов повысить эффективность алгоритмов в таких случаях является привлечение идей иерархического поиска. Алгоритмы Hierarchical А* [31] и НРА* [32,33] реализуют данные идеи в результате построения многоуровневого иерархического представления сцены и группировки смежных ячеек сетки. Данное представление затем применяется для построения путей с необходимой степенью детализации на каждом уровне иерархии.
Альтернативный алгоритм Jump Point Search, не требующий дополнительных расходов памяти, предложен в работе [34]. Он использует набор простых эвристических правил для выбора перспективных направлений, в которых могут быть предприняты длинные прямолинейные и диагональные переходы (“прыжки”). В результате из анализа исключается значительное число вершин, не влияющих на стоимость переходов и качество конечного решения, а эффективность поиска пути существенно повышается.
Маршрутные сети, построенные в пространстве сцены для некоторых типовых объектов, могут содержать переходы, непреодолимые для объектов нового типа. В подобных случаях следует попытаться проложить новый маршрут, исключающий конфликтные переходы. Наивный алгоритм мог бы состоять в повторении процедуры поиска в измененном графе с самого начала. Однако с вычислительной точки зрения такой способ не является рациональным, поскольку не учитывает предшествующие результаты.
Алгоритм LPA* [35] является развитием А* для инкрементального поиска кратчайшего пути в условиях динамического изменения весов ребер. Для каждой вершины алгоритм предусматривает хранение ее фактической стоимости у(г7) и предварительной оценки стоимости в соответствии со следующей формулой:
rhs(v) =
О , V — Vmitial minv'epredW(g(v') + c(v', v)), V * Vmitial’ где predyv) - множество ранее посещенных смежных вершин, a c(v',v) -стоимость перехода из вершины v' в вершину v. Для непосещенных вершин rhs(v) = g(v) = оо .
Приоритетная очередь LPA* содержит множество локально неустойчивых вершин, в которых оценка расходится с фактической стоимостью ^(v) * rhs^. Приоритет определяется составным ключом /c(v) = [/(Ди), /c2(v)], где k^v) = min^g(v'),rhs(v')') + h(v), k2(v) = min^g(v'),rhs(v')'), a h(v) - эвристическая оценка стоимости пути до целевой вершины.
На каждом шаге построения пути из очереди выбирается вершина с минимальным ключом. Если вершина является недооцененной ^(v) < rhs(v) и значит изменения могли повлиять на ее стоимость, то она помечается как непосещенная g(V) — со. В противном случае, если вершина является переоцененной ^(v) > r/i5(v), то она переводится в локально устойчивое состояние ^(v) = rhs(vy Далее производится переоценка смежных вершин. При любом изменении веса одного из ребер графа переоцениваются инцидентные ему вершины, а локально неустойчивые вершины добавляются к приоритетной очереди. Поиск останавливается, если выполняется условие локальной устойчивости целевой вершины или условие, при котором значение ключа целевой вершины оказалось меньше минимального значения в приоритетной очереди.
-
4.5 Алгоритм D*
-
5. Метод потенциальных полей
Часто в приложениях планирования движения возникает необходимость поиска пути в сценах с неполной, перманентно обновляемой информацией. Примером может служить задача навигации мобильного робота, получающего информацию об окружении с датчиков в режиме реального времени. При установленных изменениях в окружении робота следует перепланировать его маршрут. Для этих целей более подходят такие алгоритмы, как Focussed D* [36] и D*-light [37]. Последний использует принципы, лежащие в основе ЕРА* и, как правило, демонстрирует лучшую производительность. В работе [38] отмечается простота его реализации.
Важное семейство методов планирования движения составляют методы потенциальных полей, первоначально разработанные для навигации мобильных роботов и обхода локальных препятствий в режиме реального времени [39]. Методы основаны на физической аналогии с движением заряженной частицы в электростатическом поле. Препятствия сцены генерируют отталкивающие силы, а целевая точка маршрута - значительную притягивающую силу. Направление и скорость движения тела определяются градиентом потенциального поля (рис. 5).
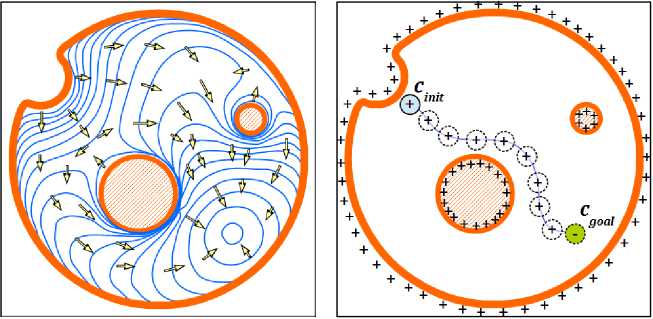
Рис. 5. Движение заряженной частицы в электростатическом поле
Fig. 5. The movement of charged particle in electrostatic field
Навигационная функция, как правило, задается суммой притягивающих и отталкивающих потенциалов: U(c) = Uatt(c) + Urep(c). При продвижении робота к целевой точке csoaz функция притягивающего потенциала Uatt должна монотонно возрастать, однако ее конкретный вид может существенно варьироваться. Например, в работе [1] предлагается следующая формула:
_ (l {D*(d(c,cgoai) — ^((D*)2, d(c,cgoai) > D*’ где d - функция, определяющая расстояние между точками, ( -масштабирующий коэффициент. D* является константным параметром, который определяет пороговое значение расстояния до цели, при достижении которого скорость движения объекта начинает снижаться. Таким способом удается избежать проблемы, связанной с “дрожанием” объекта вблизи целевой точки пути при недостаточно малом временном шаге. Функция отталкивающего потенциала, формируемого множеством препятствий 0 = {о1( о2,... о^}, задается следующим образом: Urep(c) — ^1=±игер^^>0[), \—- - A)2, о,) < D' 2 dmin(c,0i) D , О, d-mm^C> О[) > D где минимальное расстояние от заданной точки до препятствия задается функцией dmin(c,о) = minpeo((c — р||, а константный параметр D' определяет предельное расстояние от заданной точки до удаленных препятствий сцены, вклад от которых учитывается при подсчете потенциала. 5.1 Метод рандомизированных потенциальных полей 6. Сэмплинг методы Основным недостатком методов потенциальных полей, использующих градиентный спуск, является проблема локальных минимумов. Один из способов ее преодоления заключается в попытке “вытолкнуть” перемещаемый объект в случайном направлении при попадании в потенциальную яму. Данную идею реализует известный метод рандомизированных потенциальных полей (Randomized Potential Fields) [40,41]. Она же получила развитие в семействе сэмплинг-методов, подробно обсуждаемых в следующих разделах. Применение методов планирования движения, основанных на точной или приближенной реконструкции пространства допустимых конфигураций, зачастую невозможно из-за высокой вычислительной сложности, которая становится критичной для сцен с большим количеством препятствий и перемещаемых объектов со значительным количеством степеней свободы. Избежать данной проблемы позволяют популярные на сегодняшний день сэмплинг-методы планирования движения, часто ассоциируемые с методами квази-Монте Карло. Они предусматривают исследование областей конфигурационного пространства путем многократных испытаний, результатом которых является вердикт о допустимости отдельно выбранных конфигураций. Это обычно осуществляется путем генерации случайных конфигураций и проверки для них кинематических ограничений и столкновений с препятствиями сцены. На множестве полученных в результате сэмплирования бесконфликтных конфигураций строится маршрутная сеть. Важным достоинством методов данного семейства является независимость от геометрического представления и размерности моделируемого окружения. Недетерминированный характер построения маршрута привносит ряд особенностей, связанных с невозможностью обеспечения полноты алгоритмов и оптимальности найденных решений. Вместе с тем, эвристические стратегии сэмплирования обеспечивают перманентный рост вероятности нахождения бесконфликтного пути с увеличением числа итераций, естественно, если решение существует (в противном случае алгоритм может выполняться бесконечно долго). В связи с этим вводится понятие вероятностной успешности алгоритма. Определение. Алгоритм называется вероятностно успешным, если для любой задачи поиска пути (Cjree,ciltitcgoal), имеющей решение, имеет место lbTiN^,/:RiU(;,;ess = 1, где PSUCcess - вероятность найти бесконфликтный путь р(т): [0,1] CfTee , р(0) = с№, р(1) = сдоа1 за N итераций. Современные алгоритмы, основанные на сэмплировании пространства, как правило, справляются с решением типовых задач поиска пути за приемлемое время. Кроме того, их применение позволяет во многих случаях компенсировать нежелательные эффекты, связанные с неизбежными погрешностями представления геометрических моделей. Методы сэмплирования представлены двумя основными группами, а именно: методами вероятностных маршрутных сетей [42] и методами на основе деревьев поиска [43-45]. Методы успешно применяются на практике для планирования движения в пространствах высокой размерности. В частности, они широко используются для моделирования движения твердых и деформируемых тел [46,47], а также для анализа неголономных систем со сложными кинематическими связями [48,49] и дифференциальными ограничениями [50]. 6.1 Выборка конфигураций Вообще говоря, множество допустимых состояний объекта в непрерывном конфигурационном пространстве, как правило, является бесконечным. Однако маршрутная сеть должна строится за разумное число испытаний, ограниченное как размером сети, так и успешностью выбора точек при ее построении. В связи с этим, стратегия сэмплирования может являться ключевым фактором эффективности обсуждаемых методов. В идеальном случае необходимо, чтобы множество выбранных конфигураций было плотным, чтобы отражать все особенности допустимых и недопустимых областей в конфигурационном пространстве. На интуитивном уровне это означает, что наибольшая несэмплированная область пространства должна быть как можно меньше. Следующие определения параметров дисперсии и расхождения обычно используются для оценки качества выборки конфигураций [19]. Определение. Дисперсией выборки точек Р в метрическом пространстве (X, dist) называется величина, определяемая формулой 5 (В) = supxex [minpeP{dist(x,p)}j. Рис. 6 дает ее геометрическую интерпретацию в двумерном пространстве с метриками Ь2 и Ью. N (Ь) Рис. 6. Геометрическая интерпретация дисперсии выборки в метрическом пространстве Ь2(а) и L„, (Ь) Fig. 6. Geometric interpretation of the dispersion of the set of samples in metric space L2(a) andL„, (b) Параметр расхождения определяет меру того, насколько выбранные точки равномерно распределены в заданном объеме. Определение. Пусть заданы компактная область D с X в /7-мерном метрическом пространстве (X, dist) и набор прямоугольников в ней R = {г1,г2,...,гм}сО. Расхождение для выборки точек Р = {р1(р2, — ,Pn} определяется как Ө(Р,R) = supri6R |^Г^-^^|’ гДеKr) "" функция объема области г. Точки могут выбираться случайно с равномерным распределением. Однако ввиду недостатков генераторов псевдослучайных чисел данный подход, как правило, не позволяет достичь достаточно равномерного и плотного покрытия за небольшое число итераций. Улучшить качество выборки, выражаемое введенными параметрами, можно за счет использования квазислучайных последовательностей [51]. Известно, что алгоритмы квази-Монте Карло, использующие квазислучайные последовательности точек вместо псевдослучайных чисел, сходятся к искомому результату по крайней мере не медленнее, а обычно быстрее, чем соответствующие алгоритмы Монте Карло [52]. Примером таких последовательностей точек могут служить последовательности Холтона и ЛПТ-последовательности [53,54]. На рис. 7 представлен единичный квадрат, который разбит на 64 подквадрата и на него нанесены 64 псевдослучайных точки (а) и точки ЛПТ-последовательности (Ь). Видно, что в каждый квадрат на правом рисунке Puc. 7. Примеры выборок с использованием псевдослучайных (а) и квазислучайных точек (Ь) Fig. 7. An example of pseudorandom (a) and quasirandom sampling (b) Вопросы применения квазислучайных последовательностей в алгоритмах планирования движения подробно рассматриваются в работах [55,56]. 6.2 Метрика конфигурационного пространства Во всех методах маршрутных сетей и сэмплирования конфигурационного пространства требуется определять расстояние между точками выборки. В частности, это требуется при оценке дисперсии выборки в локальной области конфигурационного пространства. Вопрос о выборе функции метрики оказывается нетривиальным, поскольку влияет не только на частные характеристики выборок, но и на качество результирующей маршрутной сети в целом. Функция метрики может быть реализована путем вычисления евклидова расстояния между заданными конфигурациям по обобщенным координатам. Однако, использование такой метрики оправдано лишь в простых случаях, когда перемещение объекта ограничено поступательным движением. В более общем случае, допускающем группы вращений, например, SE(3), правильно оценить перемещение объекта без учета его геометрической модели уже невозможно. Наиболее удачный способ оценки расстояния между точками в конфигурационном пространстве заключается в определении наибольшего пути, проходимого точками тела в пространстве сцены (Robot Displacement) [57]. Метрика задается следующим образом: р^сү, с2) = тахрел{||р(с2) - pCcJH}, где р(сД - положение точки тела Л в конфигурации с,. Данная метрика позволяет оценить наибольшее расстояние, проходимое каждой точкой твердого тела или любого компонента кинематической системы в пространстве сцены при переходе из положения q, в положение q2 (рис. 8). Рис. 8. Определение расстояния между точками в конфигурационном пространстве 80(2) Fig. 8. Distance calculation between points in 80(2) configuration space Очевидно, что вычислительные затраты при использовании такой метрики существенно зависят от сложности геометрического представления объекта и его кинематических связей. Для выпуклого твердого тела, заданного полигональной поверхностью, метрика р определяется расстоянием, которое проходят только его вершины. Поэтому один из способов ее вычисления заключается в использовании предварительно построенных выпуклых оболочек или ограничивающих параллелепипедов. 6.3 Определение столкновений 6.4 Поиск ближайших соседей В ходе сэмплирования, предусматриваемого методами маршрутных сетей, необходимо определить статус допустимости или бесконфликтности каждой выбранной конфигурации объекта, в том числе, с учетом препятствий сцены. Данная задача относится к известной проблеме определения столкновений в сцене [58,59]. Как правило, определение столкновений представляет собой процесс, условно состоящий из двух основных фаз: широкой и узкой. Задачей первой фазы является быстрая локализация потенциальных столкновений с использованием относительно дешевых негативных тестов. Она эффективно решается с помощью методов ограничивающих объемов [60] и методов пространственной декомпозиции [61-63]. В узкой фазе выполняется точная проверка выбранных пар объектов на пересечение с учетом их детального геометрического представления. Существует довольно развитый математический аппарат, позволяющий эффективно выполнять данную операцию для различных видов геометрических моделей, в том числе для полиэдральных моделей [59], сплайн-поверхностей [64], твердых тел в граничном представлении [65], CSG-моделей [66] и облаков точек [67]. Формально процедуру определения столкновений можно рассматривать как (false, с Е Сггее, исчисление предиката ср (с) = ] , . для заданной конфигурации (trite, otherwise объекта с Е CfTee. Однако для объединения найденных допустимых конфигураций в маршрутную сеть требуется разрешение более сложных запросов, связанных с существованием бесконфликтных переходов между ними р(т): [0,1] -» Cfree. На практике данная проблема может быть решена путем соединения пар точек конфигураций непрерывными переходами и анализа их бесконфликтности. Для этого переходы могут быть разбиты на множество отрезков с некоторым фиксированным шагом, а каждый из концов р(т/), 1 < i < N проверен на принадлежность пространству допустимых конфигураций. Выбор шага разбиения представляет отдельную проблему. Недостаточное количество выбранных точек приведет к тому, что перемещаемый объект будет “пролетать” сквозь препятствия. Чтобы избежать данной проблемы, обычно накладывается условие ||р(т,),р(т,+1))|| < е, для всех 0 < i < N, которое определяет точность дискретного представления перехода. Повысить эффективность анализа переходов удается с помощью построения протяжек ограничивающих объемов, а также при использовании результатов проверок предыдущих точек переходов [68]. Шансы на то, что с помощью простого алгоритма поиска удастся проложить бесконфликтный путь между удаленными друг от друга конфигурациями, как правило, крайне малы. Поэтому построение маршрутной сети на множестве допустимых конфигураций производится путем соединения преимущественно близлежащих точек. Существенно повысить производительность поиска ближайших конфигураций возможно с помощью их предварительного индексирования. В частности, удается эффективно разрешать типовые запросы, связанные с поиском к ближайших точек и поиск ближайших точек в заданном радиусе, за сублинейное время. Наиболее широко используемыми для этих целей индексными структурами являются бинарные kd-деревья [69-71], которые строятся путем рекурсивного разбиения пространства гиперплоскостями, ориентированными по осям координат. Альтернативу им составляют метрические деревья, такие как, М-деревья [72], GNAT (Geometric Near-neighbor Access Tree) [73,74], iDistance-структуры [75] и деревья покрытий (Cover Tree) [76], в основе построения которых лежат алгоритмы иерархической кластеризации. Например, в ходе построения структуры GNAT формирование узлов на каждом уровне дерева выполняется путем выбора фиксированного числа опорных точек с помощью жадного рандомизированного алгоритма ^-средних. При этом принадлежность точек ветвям дерева определяется на основе матрицы расстояний до центров кластеров. При решении задач планирования движения ^-деревья демонстрируют лучшую производительность по сравнению с другими упомянутыми выше структурами [69]. Однако их практическая реализация сталкивается с проблемой адаптации процедуры пространственной декомпозиции к конкретному способу представления трансформаций объектов. Сопутствующая задача построения ограничивающих параллелепипедов становится нетривиальной в сложных конфигурационных пространствах, включающих подпространства вращения [77]. Наиболее простыми с реализационной точки зрения являются метрические деревья, для реализации которых требуется определить функцию расстояния между конфигурациями. При этом обеспечивается хорошая сбалансированность результирующей структуры. К недостаткам метрических деревьев следует отнести необходимость выбора опорных точек, от расположения и количества которых может существенно зависеть эффективность поиска ближайших соседей. 7 Оффлайн планирование. Методы вероятностных маршрутных сетей Метод вероятностных маршрутных сетей (Probabilistic Roadmap Method) [42] широко применяется для решения задач поиска путей как в локальной, так и глобальной постановке. Как и в случае ранее рассмотренных детерминированных методов маршрутных сетей, процесс планирования движения включает фазу анализа сцены и фазу построения пути. Отличительной особенностью в данном случае является способ формирования сети из локальных маршрутов, полученных в результате сэмплирования конфигурационного пространства. Puc. 9. Пример построения вероятностной маршрутной сети (к=5) ((а) 2000 итераций, (Ь)ЮООО итераций) Fig. 9. An example of probabilistic roadmap (k=5) ((a) 2000 iterations, (b)10000 iterations) В листинге 1 приводится обобщенный алгоритм построения маршрутной сети сэмплинг методом. На каждом из Nsteps шаге алгоритма генерируется точка crand в конфигурационном пространстве объекта планирования. Способ генерации новой точки определяется предопределенной стратегией сэмплирования, например, с помощью выбора точки случайным образом с равномерным распределением координат в границах конфигурационного пространства D. bounds. Затем выполняется проверка найденной конфигурации на столкновения с препятствиями сцены. Если точка оказывается конфликтной, то она отбрасывается. В успешном случае она включается в сформированное на текущий момент представление вершин маршрутной сети G. V. На следующей фазе проводится попытка расширить множество ребер маршрутной сети G.E путем отыскаяни бесконфликтных переходов между ее вершинами. В простейшем случае определяется к ближайших вершин относительно точки cTmid. В качестве альтернативного способа могут быть определены все вершины, лежащие внутри п-мерного шара радиуса г с центром в crand. Значения данных параметров могут фиксироваться или адаптивно меняться в ходе детализации маршрутной сети. Возможность создания ребра с одной из ближайших вершин определяется локальным планировщиком, в качестве которого обычно используют относительно простой и быстрый эвристический алгоритм поиска прямолинейного бесконфликтного пути. Алгоритмические особенности его реализации обсуждались в предыдущем разделе. Однако в ряде случаев возможно применение и более сложных методов. Анализ эффективности методов локального планирования при построении вероятностных маршрутных сетей приводится в работе [78]. Рис. 10. Включение новой конфигурации маршрутную сеть алгоритмом PRM Fig. 10. Construction of new roadmap vertex by PRM algorithm BuildPRM (Nsteps) l. G(V,E)<- 0 2. step<- 0 3. while (step < NstepS) 4- cTand<- SamplingStrategy. GenerateState(D. bounds) 5- if (Crartd ^ ^free) 6. G.V <- G.V и стапй 7. U <- NearestNeighbours(crcmd,G) 8. for each c^etg^our ^ ^ 9. if (LocalPlanner ҮегфуРаіһ(стт(1,сПеідһьоит)) 10. G. E *— G. E U (cTaTtd, C^eighbour) 11. step = step<- 1 7.1 Visibility PRM Листинг 1. Алгоритм построения вероятностной маршрутной сети Algorithm. 1. An algorithm of probabilistic roadmap construction Известный недостаток рассмотренного метода связан с недостаточно плотным покрытием, что может приводить к нарушению связности маршрутной сети в узких областях допустимых конфигураций. Решение проблемы путем простого увеличения количества испытаний крайне нежелательно, поскольку определение столкновений является вычислительно затратной операцией. Кроме того, успешные испытания приводят к разрастанию маршрутной сети и увеличению размерности решаемых задач поиска соседних вершин и верификации переходов. Использование индексных структур, в частности kd-деревьев, отчасти решает проблему деградации производительности. Другим недостатком метода является сложность выбора параметров, таких как радиус поиска соседних вершин и предельное количество инцидентных ребер. Данные параметры существенно влияют на качество маршрутной сети и часто требуют тонкой настройки с учетом специфики прикладной задачи. Одним из способов уменьшения числа вершин в графе является метод построения рандомизированных маршрутных сетей на основе областей видимости [79]. Данный метод позволяет исключить из анализа избыточные точки, принадлежащие обширным областям допустимых конфигураций, при этом выделив ключевые точки, существенные для навигации в труднопреодолимых зонах. Для этого в ходе формирования маршрутной сети вершины сети классифицируются как guard (страж) и connector (звено). Случайно выбранная точка относится к первому классу, если не существует вершины, помеченной как guard и лежащей в ее области видимости. Точка классифицируется как connector, если она попадает в область видимости, по меньшей мере, двух вершин guard. И наконец, если точку не удалось отнести ни к одному из двух классов, она вовсе не включается в маршрутную сеть. Тем самым достигается существенное сокращение размера маршрутной сети. К недостаткам метода следует отнести тот факт, что положение опорных точек класса guard формируется на основе случайного выбора. Поэтому области допустимых конфигураций могут быть построены и распределены неоптимальным образом, что может негативно сказаться на эффективности поиска маршрутов в определенных зонах. 7.2 Vertex Enhancement 7.3 Obstacle-based PRM Для идентификации слабо связных зон пространства допустимых конфигураций и детализации маршрутной сети в них в основную схему метода часто добавляют процедуру пост-обработки присоединяемых к сети вершин и ребер. В работе [42] для этих целей предлагается использовать информацию о неудачных попытках присоединения вершин, накапливаемую непосредственно в процессе построения сети. Вес вершины v маршрутной сети рассчитывается на основе статистики испытаний: s(v) = ^р где п£ - общее число попыток присоединения точек к V, а п^ - количество неудавшихся попыток. Таким образом, значение s(v) отражает условную сложность сцены в окрестности v. Распространяя данную оценку на множество всех вершин сети V, можно определить функцию распределения вероятностей неуспешных попыток как P(v) = и ее s(v) SveysO) использовать для генерации дополнительных точек в проблемных зонах. В ряде случаев, например, при наличии узких переходов между обширными областями допустимых конфигураций, представляется разумным выбирать точки преимущественно вдоль границ препятствий и, тем самым, снижать общее количество испытаний и размер сети. Существует ряд модификаций метода построения вероятностных маршрутных сетей, реализующих данный принцип. В методе Obstacle-based PRM, описанном в работах [80,81], для этих целей предлагается модифицировать базовый алгоритм сэмплирования следующим образом. На каждом шаге выбирается точка crand с равномерным распределением в границах конфигурационного пространства. Если найдена недопустимая конфигурация crand ё Qree, то проводится некоторое количество попыток обнаружить в ее окрестности допустимую конфигурацию с' Е Qree. На интервале прямой (crand,c') ищется новая точка cnew Е Qree, которая лежит как можно ближе к границе препятствия. Чтобы найти такую точку, можно использовать алгоритмы разбиения интервала пополам, золотого сечения или квадратичной интерполяции. Позже была предложена модификация метода UOBPRM, основанная на использовании ограничивающих параллелепипедов объектов сцены и позволяющая получать бесконфликтные точки с равномерным распределением вдоль границ препятствий [82]. 7.4 Bridge-test sampling 7.5 Gaussian PRM Аналогичный принцип применяется в эвристической стратегии сэмплирования узких проходов (Bridge-test Sampling) [83]. Данная стратегия основана на предположении о том, что если для случайно выбранной точки с е Cobs существует отрезок проходящей через нее прямой s(t) с С такой, что с = s(tQ), с’ = 5(іг) е С/гее и с" = s(t2) ё С/гее при t0 Стоит отметить, что данная стратегия, как правило, отсекает большую часть случайно сгенерированных конфигураций. Однако вычислительные затраты на определение допустимости отдельных избыточных конфигураций существенно ниже, чем на построение и анализ бесконфликтных переходов между ними. Другие модификации базового алгоритма используют Гауссово распределение для формирования выборок с большей плотностью вблизи границ препятствий [84] . По аналогии с формулой размытия, применяемой в алгоритмах обработки изображений, нормальное распределение Гаусса в конфигурационном пространстве С определяется как ^(с,g) — Т_пе м\ где с е С, и - 7.6 Medial axis PRMs 7.7 Lazy-PRM Функция размытия определяется следующим образом: Л с, ст) = f Obs(y) где Obs(q) = L г С t lyree Для того, чтобы исключить недопустимые конфигурации, распределение задается как у(с,g) = max(0,/(c,а) - Obs(c)y Тем самым, функция у(с,ц) принимает значение 0 для всех недопустимых конфигураций и тождественна функции /(с) для допустимых. Параметр а определяет близость генерируемых конфигураций к границам препятствий. Алгоритм построен таким образом, что первая точка выбирается случайным образом с равномерным распределением, а каждая следующая - с распределением, соответствующим приведенной выше формуле. Альтернативный принцип формирования выборок заключается в том, что предпочтение отдается конфигурациям равноудаленным от препятствий сцены [85-87]. Один из возможных способов его реализации заключается в предварительном построении срединной оси в пространстве сцены, которая используется для генерации новых точек. Характерным недостатком вероятностных маршрутных сетей является избыточность их представления, поскольку на практике для построения путей обычно требуется гораздо меньшее количество вершин. Это приводит к тому, что значительная часть времени выполнения алгоритма расходуется на вычислительно затратную операцию определения столкновений для конфигураций, несущественных для построения маршрута. Для устранения данного недостатка были предложены методы Fuzzy-PRM [88] и Lazy-PRM [89,90] с отложенной проверкой на бескофликтность переходов между конфигурациями. Алгоритм поиска пути может быть представлен следующим образом (листинг 2). Вначале строится маршрутная сеть алгоритмом, аналогичным PRM, с тем исключением, что ребра не верифицируются локальным планировщиком (строка 1). Далее предпринимается попытка построить путь в сети (строка 5). В процессе построения ребра проверяются на бесконфликтность (строки 7-11), а конфликтные ребра удаляются из представления маршрутной сети (строка 10). В случае, если не удалось построить достоверный маршрут, соединяющий начальную и конечную конфигурации, разрешение маршрутной сети 264 увеличивается путем дополнительной генерации точек в слабо связных областях допустимых конфигураций (строка 13). LazyPRM (сіпцEgoal’ К steps, ^samples) l.G(V,E) - PRM(Nsampies) 2.success <- false 3.step<- 0 4. while ( (step < Ksteps) & (success = false) ) 5. p(V',E') <- FindShortestPath(G, Сіпц, cgoal) 6. if (p * 0) 7. success <- true 8. for each е Ep.E' 9. if (e 4 CfTee) 10. G.E = G.E\e 11. success <- false 12. else 13. VertexEnhancement( G, Nsamples ) 14. step = step<- 1 7.8 Dynamic PRM 8. Онлайн планирование. Деревья поиска 8.1 Нить Ариадны Листинг 2. Алгоритм поиска пути на основе вероятностной маршрутной сети с отложенной проверкой на бесконфликтность Algorithm 2. Probabilistic roadmap algorithm with lazy collision checking Вероятностные маршрутные сети позволяют значительно повысить эффективность поиска пути в случае повторных запросов, поскольку вычислительные затраты на предварительный анализ сцены и формирование исходной маршрутной сети уже осуществлены. Однако данное утверждение справедливо исключительно для статических сцен. В случае динамики использование метода затруднительно, поскольку разворачивание новой маршрутной сети при каждом изменении в сцене представляется крайне неэффективным. Существует ряд модификаций метода, позволяющих перестраивать маршрутную сеть более рациональным образом [91-93]. Одним из известных сэмплинг-методов планирования движения на основе деревьев поиска является алгоритм “Нить Ариадны” [94,95]. Алгоритм строит маршрутную сеть таким образом, чтобы на каждом шаге покрыть как можно большую новую область конфигурационного пространства, не подлежащую анализу на предыдущих шагах. В зависимости от успешности распространения алгоритм переключается в один из двух возможных режимов: режим поиска или режим анализа. В режиме анализа осуществляется рандомизированный выбор опорных точек, или “ориентиров”, максимально удаленных от вершин разворачиваемой сети. В режиме поиска предпринимается попытка присоединить целевую конфигурацию к одному из ориентиров, найденных в режиме анализа. Ключевым принципом алгоритма является перераспределение вычислительных ресурсов на анализ пространства сцены вместо исключительного продвижения к целевой конфигурации. Это позволяет повысить эффективность маршрутизации в сложных сценах за счет снижения роли “жадной” эвристики в поиске пути и его глобализации. Примечательно, что данный принцип получил свое развитие и в других алгоритмах данного семейства. В качестве недостатка алгоритма следует указать высокую вычислительную сложность сопутствующей оптимизационной задачи выбора новой вершины в режиме анализа. Для преодоления этой проблемы предлагалось использовать генетические алгоритмы [95], но целесообразность их применения в данном случае вряд ли можно считать оправданной ввиду необходимости настройки множества параметров, специфичных для каждой прикладной задачи планирования движения [19]. 8.2 Random-Walk Planner 8.3 Expansive-Spaces Tree Planner Простой в реализации и в то же время достаточно эффективный алгоритм поиска пути Random-Walk Planner описан в работе [96]. Представленный алгоритм построен исключительно на рандомизированных перемещениях в конфигурационном пространстве, не используя никакой маршрутной сети. Направление движения и длина шага определяются на каждой итерации случайным образом на основе нормального гауссова распределения. При этом матрица ковариации формируется на основе фиксированного числа последних испытаний. Таким образом, параметры, определяющие способ распространения, адаптивно настраиваются в ходе работы алгоритма. При этом добавление в путь каждой новой вершины выполняется за константное время в отличие от методов на основе маршрутных сетей. Основную проблему для описанного алгоритма составляют сцены с узкими проходами и длинными коридорами. Для ее преодоления предложен гибридный вариант, объединяющий базовый алгоритм Random-walk Planner и рандомизированный метод потенциальных полей [97]. Планировщик на основе EST-деревьев (Expansive-Spaces Tree planner), описанный в работах [43,98,99], реализует некоторые принципы методов вероятностных маршрутных сетей применительно к разрешению одиночных запросов поиска пути. Стратегия сэмплирования в данном методе построена таким образом, чтобы предпочтение отдавалось областям конфигурационного пространства с наименьшей плотностью покрытия маршрутной сетью. Для этого вводится понятие веса конфигурации, который определяется количеством вершин маршрутной сети, лежащих в некоторой окрестности радиуса R от данной точки: w(c, R) = |{v е V\Dist(c, v)< R}|. На каждой итерации алгоритма выбирается вершина дерева с вероятностью обратно пропорциональной ее весу. Далее в заданном радиусе генерируется К случайных бесконфликтных конфигураций и предпринимается попытка их включения в маршрутную сеть (листинг 3). В работе [98] изложен способ повышения производительности алгоритма за счет двунаправленного поиска на основе EST деревьев с отложенной проверкой на бесконфликтность конфигурации (Single Query, Bidirectional Lazy Collision Checking). К недостаткам рассмотренного алгоритма можно отнести то, что успех поиска сильно зависит от значений константных параметров R и К, которые следует выбирать с учетом особенностей решаемой прикладной задачи. EST (Сіпц. Nsteps,K, R) /.Г(Е,£)^({смД,0) 2. step<- О 3. while (step < Nsteps) 4. v <- PickNodeWithProbability(r,-^-^ 5. U <- GenerateStates(K, {c e Cfree\Dist(.c,'v')< Д}} 6. for each и E U 7. if (RetainWithProbability ( ^ R^) 8. if (e(u,v) e CfTee ) 9. T.V^T.VUu 10. T.E-T.E'Moj 11. step <- step + 1 8.4 Rapidly Exploring Random Trees Листинг 3. Алгоритм построения EST дерева Algorithm 3. EST tree construction algorithm Алгоритм на основе быстро растущих случайных деревьев (Rapidly Exploring Random Tree) был изначально разработан для планирования движения неголономных механических систем в режиме реального времени [44,50]. По сравнению с другими известными сэмплинг-методами, эффективность которых зависит от большого количества настраиваемых входных параметров, алгоритм RRT является наиболее универсальным средством решения широкого круга задач планирования движения. Данный алгоритм использует в качестве дискретного представления конфигурационного пространства дерево, корень которого соответствует исходному положению объекта. Дерево достраивается таким образом, чтобы разрешение получаемой маршрутной сети увеличивалось на всем пространстве допустимых конфигураций (рис. 11). Таким образом, RRT деревья обладают свойствами, во многом схожими с кривыми, заполняющими пространство (Space-Filling Curves) [100]. Рис. И. Пример построения дерева поиска алгоритмом RRT ((а) 1000 итераций, (Ь)20000 итераций ) Fig. И. An example of search tree construction by RRT algorithm ((a) 1000 iterations, (b)20000 iterations ) Рассмотрим алгоритм распространения RRT дерева (листинг 4). На каждой итерации выбирается случайная точка cranci е С. Далее ищется ближайшая к ней вершина дерева cnenr е Т. Отрезок прямой р' = [cnear, crand] проверяется на конфликтность. В процессе проверки определяется точка cnew = Г гслиъ Р, freecst0T - бесконфликтная конфигурация на данном отрезке V^stop, Р ^free такая, что [cnear, cs£op] Е р' П CfTee и ||cs£op,Cobs П р'|| < е, а е - погрешность определения конфликтов (рис. 12). Точка cnew и ребро [cnear, cnew] включаются в маршрутную сеть при условии cnew 4 crand. Рисунок 12. Включение новой конфигурации в дерево поиска алгоритмом RRT Fig. 12. Construction of new tree vertex by RRT algorithm Важно отметить, что алгоритм распространения построен таким образом, что вероятность выбора каждой вершины дерева пропорциональна объему региона вороного, которому она принадлежит. Данная особенность алгоритма обуславливает высокую скорость “разрастания” дерева в пространстве. RRT (Сіпц. СдоаО blsteps-blextend- Р) LTiy.E^^^CtnitW 2.s tep<- О 3.s uccess <- false 4. while ((step < Nsteps) & (success=false) ) 5. if (step mod Nextend * 0) 6. Crand ^ GenerateStateQ 7. else 9. cnear<- NearestNeighbour(crand,T) 10. cnew<~ FindStoppingState(c,1(,(IT, cr(I)1 d, p) 12. T.V = T.VUc„ 13. T.E = T.E U (c„ear, c„ew) 14. success <- ^Distance(cnew, cgoal) < p) 15. step <- step + 1 16. return success 8.5 RRT-Connect О- СГаТгД CgOal H- if (cnew Ф cnear ) Листинг 4. Алгоритм поиска пути с использованием RRT дерева Algorithm 4. Path planning using RRT algorithm Поиск пути осуществляется в результате периодически предпринимаемых попыток включить целевую конфигурацию в маршрутную сеть. Следует отметить, что частое выполнение данной операции повлечет за собой неоправданное завышение вычислительных затрат, свойственное методам локального планирования и, в частности, методам потенциальных полей. В качестве одного из способов повышения эффективности классического метода RRT-деревьев было предложено использовать двунаправленный поиск [50,101]. Рис. 13. Пример построения деревьев поиска алгоритмом RRT-connect ((а) 250 итераций, (Ь)964 итерации) Fig. 13. An example of search trees construction by RRT-connect algorithm ((a) 250 iterations, (b)964 iterations) Для формирования маршрутной сети в алгоритме RRT-connect (листинг 5.) используется пара деревьев Тг и Т2, корням которых соответствуют начальная конфигурация С[пр и конечная конфигурация сдоа1 искомого пути. На каждом шаге одно из деревьев дополняется новыми бесконфликтными конфигурациями в соответствии с алгоритмом RRT. Однако вместо периодических попыток включения сдоа1 выполняется операция сращивания деревьев. При каждом включении новой вершины в Тг предпринимается аналогичная попытка включить ее и в Т2. При выполнении некоторого количества шагов деревья меняются ролями, что обеспечивает их более сбалансированный рост. Алгоритм построен таким образом, что предпочтение отдается тому дереву, распространение которого затруднено (например, в связи с наличием большого количества препятствий в его области). Количественным критерием в данном случае может служить общее число вершин дерева или суммарная длина ребер. RRTConnect (сіпц, CgOai, NstepS,p ) LW.E)^ ({ciniJ,0) -7W,F) - ({c5Oai},0) 4. success <- false 5. while ((step < Nsteps) & (success=false) ) 6. crcmd<- GenerateState () 7. cneaT<- NearestNeighbour(crcmd,T1) 10. T1.V = T1.VUcnew 11. TVE = TVE U(cnear,cnew) 12. Cnear *- NearestNeighbour(cnew,T2) 13. tyew ^~ FiudStoppiugState(cneaT, cnew, p) 14. if ( Cytew ^ ^yteay ) 15. T2.V = T2.V U c*ew 16. Tv E=TvEV (,C^ear- C^ew) 17. success <- (Distance^Cnew, c„ew)< p) 18. if (\T2\ > |W 19. Swap( Tt, T2 ) 20. step <- step + 1 21. return success 8.6 Execution Extended RRT J. step <- О 0- Cnew *~ FindStoppingState(cnear, crar[d, p) ^- if (cnew 7^ cneaT ) Листинг 5. Алгоритм двунаправленного поиска пути с использованием RRT деревьев (RRT-connect) Algorithm 5. Bidirectional version of RRT algorithm (RRT-connect) Существует ряд работ, посвященных применению многих быстро растущих деревьев для локального планирования [102-104], однако вопрос о разумном компромиссе между количеством разворачиваемых деревьев и затратами на их распространение остается открытым [19]. В работе [105] предлагается способ повысить эффективность исполнения множественных запросов планирования движения за счет кэширования бесконфликных конфигураций. Таким образом, каждый последующий запрос планирования использует бесконфликтные переходы, обнаруженные в результате работы RRT алгоритма ранее. Данная идея хорошо сочетается с двунаправленным поиском. Предложенный алгоритм Multi-Bridge ERRT [106] заимствует основной принцип RRT-connect, однако процедура распространения деревьев продолжается и после сращивания. Ввиду того, что структура, полученная в результате работы алгоритма уже не является деревом, результирующий путь ищется в графе с помощью алгоритма А*. 8.7 Dynamic Domain RRT Как было отмечено, на каждой итерации RRT алгоритма вероятность выбора вершины дерева прямо пропорциональна объему региона Вороного, которому она принадлежит. Данный факт обуславливает высокую скорость разрастания дерева в конфигурационном пространстве. Однако распространение может быть затруднено в тех случаях, когда внешние вершины дерева распределены преимущественно вдоль границ препятствий, а покрываемая деревом область конфигурационного пространства относительно невелика. В качестве примера можно привести ситуацию, когда начальная точка пути находится внутри небольшой комнаты с единственным узким проходом (рис. 14 а, Ь). Если новые конфигурации генерируются с равномерным распределением во всем доступном объеме, то вероятность попадания случайно выбранной точки в область прохода может быть ничтожно мала. Для решения описанной проблемы в работе [107] был предложен алгоритм Dynamic Domain RRT, динамически ограничивающий область сэмплирования в ходе формирования дерева. Для RRT дерева, построенного на множестве вершин V, вводится понятие динамической области 0 = V)vevDomarn.(v,Ry Каждый фрагмент области определяется как Domain^v, R) = (D(v) n BR(vy min(||v,Cobs||) < s lo(O, ™n(lk,C01,sID > =■ ™ DW " pe™°H B°p°"oro- которому принадлежит вершина v, a BR(v) - шар радиуса R с центром в v (рис. 14, с). Рис. 14. Регионы Вороного, построенные на множестве вершин RRT дерева (а, Ь) и динамическая область сэмплирования (с). Fig. 14. Voronoi regions associated with the nodes of tree constructed by RRT planner (a, b) and dynamic sampling domain (c). 2. step<- 0 3. while ( step < Nsteps) 4. repeat 5. cTan(1 GenerateState(T. bounds) 6. Cnear NearestNeighbour(crand,T) 7. until (DistcmceQcnear, Grand) < cnear■'radius) 9. if ( Cnew 7^ Cnear ) 10. Cnew■ radius <- oo 11. T.V = T.VUCnew 12. T.E =T.E U (Cnear. Cnew) 13. else 14. Cnew-гadius <- R 15. UpdateBounds( Tbounds, Cnew ) 16. step = step<- 1 8.8 Iterative Diffuse Path Planner Алгоритм построен таким образом, что распространение маршрутной сети осуществляется за счет конфигураций, принадлежащих динамической области О (листинг 6). В ходе построения дерева вершины помечаются как внешние или внутренние. Включение случайно выбранной точки cTmd е С в дерево выполняется лишь при условии, что ближайшая к ней вершина является внутренней или лежит от нее на расстоянии, меньшем R. Значение радиуса R рекомендуется выбирать, исходя из максимально допустимой погрешности определения конфликтов, определяемой, например, линейной функцией R = Ле, где Л - положительный целочисленный коэффициент. DynamicDomainRRT (emit, Nsteps,R) l.T(V ,Е) ({cinM $■ Cnew *~ FIndStOppingStateQcnear> Grand) Листинг 6. Построение дерева в алгоритме Dynamic-Domain-RRT Algorithm 6. Construction of tree using Dynamic-Domain-RRT algorithm Применение метода RRT деревьев вместе с лежащей в его основе “жадной” эвристикой может быть крайне нежелательным для ряда задач планирования движения. Примером может служить задача автоматической разборки изделий, состоящих из множества деталей. Движение детали вблизи исходной конфигурации, как правило, сильно ограничено, и возможно лишь за счет малых поворотов. И наоборот, в области целевой конфигурации, находящейся на значительном удалении, препятствия вовсе отсутствуют. Принцип отложенной проверки на бесконфликтность конфигураций в сочетании с динамически изменяемой погрешностью лежит в основе диффузионного алгоритма планирования движения (Iterative Diffuse Path Planner) (листинг 7). Алгоритм позволяет значительно повысить эффективность поиска в постановках, подобных приведенной [45]. В данном алгоритме используется лес растущих деревьев. Распространение осуществляется из произвольной вершины в направлении, определяемом случайным вектором, с шагом, равному текущему значению погрешности 273 определения конфликтов с. После включения каждой новой вершины в дерево предпринимается попытка его слияния. Верификация ребер на конфликты в процессе распространения не выполняется. Значение о инициализируется достаточно большим значением, например, равным расстоянию между Cjnjt и cgoai, и итерационно уменьшается вплоть до заданного минимально допустимого значения. На каждой итерации выполняется поиск пути описанным выше способом с последующей его верификацией. В случае, если путь оказался конфликтным, из представления деревьев исключаются все ребра, не прошедшие проверку, а процедуры распространения и поиска пути повторяются. DiffuseRRT (Т(ҚЕ), а) I .vrand ChooseRandomNodefT. V) 2 .cTand ^" ShootNearNode^and) 5. if (cnew Ф ^near) 6. T. V <- T. V U cnew 7. T. Е ^ T. E U (linear, Cnew) 8. for each Г e G\T 9. LinkTrees(Cnew>T*) 3-Vnear NearestNeighbour(crand,T) ^■^new FindStoppingState(ynear, CTand) IterativeDiffusionPathPlanner (С(пц,сдОаьЕ 7 l .GQV.E)<- 0 2 .cr *- Distctnce^Cinitf Cgoai) 3 .while (a > e) 4 . р(У',Е') <- DiffuseRRTQctnit' Cgoai»G.a) 3. a a/a 6. for each е Ep.E' 7. if (e 0 CfTee) 8. G.E^G.E\e 9. p DiffuseRRTQcinit,cgoal,G) 10. return p 9. Поиск оптимальных путей сэмплинг-методами 9.1 Офлайн оптимизация 9.2 Онлайн оптимизация Листинг 7. Итеративный дифузионный алгоритм поиска пути Algorithm 7. Iterative diffuse path planning algorithm Удовлетворяя требованиям вероятностной успешности, рассмотренные выше сэмплинг-методы с успехом применяются к практическим задачам планирования движения, прежде неразрешимым за приемлемое время. Однако рандомизированный характер поиска, присущий PRM и RRT методам, крайне негативно влияет на качество получаемых решений. Подразумевается, что в качестве количественных критериев качества решений могут выступать длина и гладкость траектории, расстояние между движущимся объектом и препятствиями сцены, стоимость преодоления препятствий, затраты энергии и т.п. Один из подходов к решению данной проблемы состоит в пост-обработке найденных бесконфликтных путей, основанной на их итерационной локальной оптимизации. Довольно простым и популярным является итерационный алгоритм укорачивания пути [2]. На каждом шаге алгоритма выбирается пара точек, лежащих на пути. Первая точка выбирается случайно, а вторая - в некотором радиусе от нее. Причем точки не обязаны совпадать с вершинами пути. Далее точки соединяются отрезком прямой в конфигурационном пространстве, а отрезок проверяется на бесконфликтность или, другими словами, на принадлежность пространству допустимых конфигураций. В случае успеха все точки, лежащие между выбранными на исходном пути, выбрасываются, а отрезок включается в представление пути. В результате пост-обработки, как правило, получается семейство гомотопных путей и, следовательно, оптимальное решение может быть недостижимо. Альтернативный способ оптимизации пути состоит в гибридизации или объединении участков из нескольких ранее найденных бесконфликтных путей [108]. Несмотря на то, что RRT и PRM методы не учитывают характер переходов между конфигурациями, улучшить получаемые решения возможно путем модификации базовых алгоритмов. Оптимизация может осуществляться как за счет изменения способов распространения в пространстве [109,110], так и за счет изменения правил включения бесконфликтных конфигураций в маршрутную сеть [3]. 9.3 Heuristic RRT 9.4 Transition-based RRT Несколько иной способ повысить качество путей предложен в работе [109]. В алгоритме hRRT (Heuristic RRT) вводится дополнительная эвристика, корректирующая функцию распределения вероятностей при выборе новых конфигураций таким образом, чтобы отдавать предпочтение путям наименьшей стоимости. Вероятность выбора конфигурации определяется двумя факторами. Во-первых, как и в базовом алгоритме RRT, она зависит от объема региона Вороного, которому она принадлежит. А во-вторых, она определяется предполагаемой стоимостью пути, проходящего через данную конфигурацию. Для этого вводится следующая оценка: mquaUty = 1 — cvertex~ copt ~ i -------—, где cuertex - суммарная стоимость пути из начальной конфигурации стах copt в данную вершину и из данной вершины до целевой конфигурации, copt -предполагаемая стоимость оптимального пути из начальной конфигурации в целевую, а стах - максимальная стоимость пути до любой вершины дерева на текущем шаге. Таким образом, числитель представляет собой оценку отклонения от предполагаемого оптимального пути, а знаменатель служит масштабирующим коэффициентом для нормирования результата. Данная оценка используется при сэмплировании конфигурационного пространства. На каждом шаге RRT алгоритма случайным образом выбирается несколько конфигураций, однако в дерево включается конфигурация с наименьшей стоимостью пути. Эвристика, применяемая в алгоритме hRRT, заставляет прорастать дерево к целевой конфигурации, часто игнорируя при этом более оптимальные пути. Метод T-RRT (Transition-base RRT) больше подходит для планирования движения в сложных стоимостных пространствах [ПО]. Для выбора конфигураций наименьшей стоимости в данном методе используется алгоритм имитации отжига (Simulated Annealing). Решение о включении новой конфигурации в дерево принимается с учетом ее стоимости относительно стоимости ближайшей вершины. Вероятность включения конфигурации с при заданной функции стоимости /(с) определяется следующим образом: Р(с) = f ехр (- , А/ > О . ] \ ктJ , где А/ - отношение приращения стоимости между 9.5 PRM* RRT* I 1,Д/<0 конфигурациями к расстоянию между ними А/ = —^^ _ dist(cnear,cnew) f(cinit)+f(cgoal) .., , ------—-— - нормирующий коэффициент, рассчитываемый как среднее значение стоимости начальной и целевой конфигураций, а Т - числовой параметр, называемый температурой. Таким образом, чем больше приращение стоимости, тем меньше вероятность включения конфигурации в дерево. При этом допускаются все переходы в конфигурации с меньшей стоимостью. Параметр Т позволяет контролировать характер поиска. При очень высоких значениях температуры принимаются почти все новые точки. При низких значениях - распространение происходит преимущественно за счет исключительных точек, увеличивающих стоимость пути незначительно. Процесс поиска начинается при низкой температуре, а затем продолжается при возрастающих значениях температуры, которая повышается всякий раз когда количество точек, не удовлетворяющих критерию включения в дерево, достигает заданного предельного значения. В работе [3] предложены модификации алгоритмов PRM и RRT, предназначенные для получения асимптотически оптимальных решений. Определение. Алгоритм ALG асимптотически оптимален, если он вероятностно успешен, а также для любой задачи поиска пути (Qree, С{Пц сдоп[) со стоимостной функцией fc(p) и оптимальным решением р* имеет место Р^Нти^ю sup YnLG = fc(P*)}) = 1, где YPLG - минимальное значение стоимости для всех решений, полученных за и шагов алгоритма. RRT* повторяет базовый алгоритм RRT за исключением процедуры включения новых конфигураций в дерево поиска (листинг 8). Данная процедура построена таким образом, чтобы стоимость путей, входящих в дерево, уменьшалась с каждым шагом алгоритма. В ходе построения дерево поиска дополняется значениями стоимости пути, ведущего в каждую из его вершин. Как и в базовом алгоритме, на каждом шаге для случайным образом выбранной точки стаиД ищется ближайшая вершина графа cnear, а также точка cnew е Qree, полученная в результате распространения из сиеат в стаиД (строки 4-7). Далее определяется подмножество вершин дерева С*, лежащих внутри шара радиуса г с центром в cnew. Среди них находят вершину cmin такую, что стоимость пути из начальной конфигурации cini£ в cnew была минимальной (строки 8-10). После того как cnew включается в дерево в качестве дочернего узла cmin (строки 11-12), проводится локальная оптимизация путей внутри шара. Для каждой конфигурации в нем с' е С* предпринимается попытка построения пути, ведущего в cnew, и в случае, если он имеет меньшую стоимость, то конфигурация с' становится дочерней вершиной cnew (строка 13). Радиус поиска в данном алгоритме представляет собой функцию от количества вершин дерева и адаптивно уменьшается с его детализацией. В работе [3] доказывается, что алгоритм RRT* асимптотически оптимален при г(|1Д) = RRTStar (cinit,Nsteps) 2. step<- 0 3. while ( step < Nsteps) 4. cTmd<- Generate State 0 5. cnear NearestNeighbour(crand,T) 6- Cnew FindStoppingS tate(cl1H,lT> cranf) 7. If ( cnew Ф cnear ) 8. r <- SearchRadius(step) 9. C* <- NearestNeighbours(cnew,T,f) 10. cmin<- MinCostParent(C*) 11. T.V = T.V\Jc„ 12. T.E =Т.Еи(рті]ІІс,е1А 13. Rewire(T C , cmin, cnew) 14. step = step<- 1 Листинг 8. Построения дерева поиска алгоритмом RRT* Algorithm 8. Construction of tree using RRT* algorithm В последние годы методы PRM* и RRT* получили дальнейшее развитие. Разработано большое количество алгоритмов, демонстрирующих более высокие показатели эффективности поиска и обладающих лучшей сходимостью к оптимальным решениям. В работах [111,112] предложены алгоритмы Lazy-PRM* и Lazy-RRG*, реализующие принцип отложенной проверки на конфликты. Оба алгоритма асимптотически оптимальны и в ряде случаев позволяют ускорить поиск пути. Для устранения проблемы избыточного количества ребер в маршрутных сетях, полученных в результате работы алгоритма PRM*, были предложены модификации для поиска путей, близких к оптимальным. В основе алгоритма IRS [113-115] лежит инкрементальный способ построении а-спаннера графа. При количестве итераций, стремящемся к бесконечности, и заданном коэффициенте а алгоритм сходится к оптимальному решению с точностью 1 + а и вероятностью, равной единице. Схожий принцип используется в алгоритме SPARS, который заимствует идеи инкрементального построения спаннера и отсечения точек на основе областей видимости [116,117]. Для повышения скорости сходимости к оптимальному решению было предложено дополнить алгоритм RRT* процедурой перепланирования, не ограничивающейся локальной оптимизацией ребер. В алгоритмах RRT*-smart [118] и RRT# [119] участки, потенциально являющиеся частью оптимального пути наименьшей стоимости, оптимизируются по всей длине, начиная от корня дерева. В работе [120] описывается асимптотически оптимальный алгоритм FMT* (Fast Marching Tree), который строит маршрутную сеть на множестве случайных бесконфликтных конфигураций и одновременно поддерживает ее остовное дерево с корнем в начальной точке пути и минимальными значениями стоимости путей до его вершин. Алгоритм LBT-RRT (Lower Bound Tree RRT) [121], также являющийся развитием RRT*, позволяет повысить эффективность поиска за счет смягчения требования асимптотической оптимальности. Для планирования движения в сложных стоимостных пространствах был разработан гибридный алгоритм TRRT*, использующий алгоритм имитации отжига [122]. В работах [123,124] были предложены модификации RRT* и ҒМТ*, использующие двунаправленный поиск. 10 Заключение Таким образом, в работе представлен обзор задач и методов современной теории планирования движения. Рассмотрены основные факторы, определяющие особенности прикладных задач и влияющие на выбор применяемых математических методов. К ним отнесены характер постановки планирования движения (локальный или глобальный), геометрическое представление перемещаемого объекта (твердое тело или кинематическая конструкция), свойства окружения (статическое или динамическое), свойства конфигурационного пространства (равномерное распределение допустимых состояний или наличие узких областей), характер запросов планирования (однократный или многократный). Также представлены основные подходы к планированию движения, связанные с пространственной декомпозицией сцены, физическими аналогиями с потенциальными полями, маршрутными сетями и быстро растущими деревьями. Детально рассмотрены ключевые методы и алгоритмы, реализующие данные подходы, и аспекты их практического применения. Предполагается, что обзор поможет в выборе методов с учетом особенностей решаемых прикладных задач и в их эффективной программной реализации и настройке. Ожидается также, что обзор послужит основой для систематизации и объектной концептуализации теории планирования движения, необходимой для создания единой программно-инструментальной среды разработки приложений.
Список литературы Обзор современных методов планирования движения
- Choset H., Lynch K., Seth H., Kantor G., Burgard W., Kavraki L.E., Thrun S. Principles of Robot Motion-Theory, Algorithms, and Implementation. MIT Press, 2005.
- Geraerts R., Overmars M.H. Creating High-quality Paths for Motion Planning. Int. J. Rob. Res., vol. 26, № 8, 2007, pp. 845-863.
- Karaman S., Frazzoli E. Sampling-based algorithms for optimal motion planning. Int. J. Robot., vol. 30, № 7, 2011, pp. 846-894
- Laumond J.-P. Kineo CAM: A success story of motion planning algorithms. IEEE Robot. Autom. Mag., vol. 13, № 2, 2006, pp. 90-93.
- Rockel S., Klimentjew D., Zhang L., Zhang J. An hyperreality imagination based reasoning and evaluation system (HIRES). Proc. IEEE Int. Conf. on Robotics and Automation, 2014. pp. 5705-5711.
- Sucan I., Moll M., Kavraki L.E. The Open Motion Planning Library. IEEE Robot. Autom. Mag. vol. 19, № 4, 2012, pp. 72-82.
- Diankov R. Automated Construction of Robotic Manipulation Programs. PhD thesis, Carnegie Mellon University, Robotics Institute, August 2010, 263 p.
- Porta J.M., Ros L., Bohigas O., Manubens M., Rosales C., Jaillet L. The CUIK Suite: Motion Analysis of Closed-chin Multibody Systems. IEEE Robot. Autom. Mag., vol. 21, № 3, 2014, pp. 105-114.
- Semenov V.A., Kazakov K.A., Zolotov V.A. Effective spatial reasoning in complex 4D modeling environments. eWork Ebus. Archit. Eng. Constr. eds. A.Mahdavi, B. Martens, R. Scherer, CRC Press. Taylor Fr. Group, London, UK. 2015, pp. 181-186.
- Kazakov K.A., Semenov V.A., Zolotov V.A. Topological Mapping Complex 3D Environments Using Occupancy Octrees. 21st Int. Conf. Comput. Graph. Vision, Sept. 26-30, 2011, Moscow, Russ. 2011, pp. 111-114.
- Semenov V.A., Kazakov K.A., Morozov S. V., Tarlapan O.A., Zolotov V.A., Dengenis T. 4D modeling of large industrial projects using spatio-temporal decomposition. eWork Ebus. Archit. Eng. Constr. eds. K. Menzel R. Scherer, CRC Press. Taylor Fr. Group,London, UK. 2010, pp. 89-95.
- Brooks R.A., Lozano-Peres T. A Subdivision Algorithm in Configuration Space For Find Path with Rotation. IEEE Trans. Syst. Man. Cybern., vol. SMC-15, № 2, 1985, pp. 224-233.
- D. Zhu and J.-C. Latombe. Constraint reformulation in a hierarchical path planner. In Proc. IEEE Int. Conf. on Robotics and Automation, 1990, pp. 1918-1923.
- Hornung A., Wurm K.M., Bennewitz M., Stachniss C., Burgard W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robots., vol. 34, № 3, 2013, pp. 189-206.
- Semenov V.A., Kazakov K.A., Zolotov V.A. Global path planning in 4D environments using topological mapping. eWork Ebus. Archit. Eng. Constr. 2012, pp. 263-269.
- Chen D.Z., Szczerba R.J., Uhran Jr J.J. Using Framed-Quadtrees to Find Conditional Shortest Paths in an Unknown 2-D Environment. Technical Report #95-2, Department of Computer Science and Engineering, University of Notre Dame, Notre Dame, Indiana, Jan. 1995, 33 p.
- Chazelle B. Approximation and Decomposition of Shapes. Advances in Robotics 1: Algorithmic and Geometric Aspects of Robotics, 1987, pp. 145-185.
- De Berg M., Cheong O., Van Kreveld M., Overmars M. Computational Geometry: Algorithms and Applications. 3rd Edition. Springer-Verlag, 2008, 386 p.
- LaValle S.M. Planning Algorithms. Cambridge University Press, 2006, 844 p.
- Canny J.F., Lin M.C. An opportunistic global path planner. Algorithmica, vol. 10, № 2-4, 1993, pp. 102-120.
- Huang H.-P.H.H.-P., Chung S.-Y.C.S.-Y. Dynamic visibility graph for path planning. Proc. Int. Conf. Intell. Robot. Syst., vol. 3, 2004, pp. 2813-2818.
- Kaluder H., Brezak M., Petrovic I. A visibility graph based method for path planning in dynamic environments. MIPRO, 2011, Proceedings of the 34th International Convention, Opatija, Croatia, 2011, pp. 717-721.
- Aurenhammer F. Voronoi Diagrams -A Survey of a Fundamental Data Structure. ACM Comput. Surv., vol. 23, № 3, 1991, pp. 345-405.
- Choset H. Sensor based motion planning: The hierarchical generalized voronoi graph. Ph.D. Thesis, California Institute of Technology, 1996, 201 p.
- Russell S.J., Norvig P. Artificial Intelligence: A Modern Approach. Neurocomputing, vol. 9, № 2, 1995, pp. 215-218.
- Bell S., An Overview of Optimal Graph Search Algorithms for Robot Path Planning in Dynamic or Uncertain Environments. Oklahoma Christian University, 2010, 9 p.
- De Filippis L., Guglieri G. Advanced graph search algorithms for path planning of flight vehicles. Recent Adv. Aircr. Technol., 2012, pp. 159-192.
- Zeng W., Church R.L. Finding shortest paths on real road networks: the case for A*. Int. J. Geogr. Inf. Sci., vol. 23, № 4, 2009, pp. 531-543.
- Korf R.E. Depth-first iterative-deepening. An optimal admissible tree search. Artif. Intell., vol. 27, № 1, 1985, pp. 97-109.
- Zhou R., Hansen E.A. Memory-Bounded {A*} Graph Search. The Florida AI Research Society Conference -FLAIRS, 2002, pp. 203-209.
- Holte R., Perez M., Zimmer R., MacDonald A. Hierarchical A*: Searching abstraction hierarchies efficiently. Proceeding AAAI'96 Proceedings of the thirteenth national conference on Artificial intelligence -Volume 1, 1996, pp. 530-535.
- Botea A., Muller M., Schaeffer J. Near optimal hierarchical path-finding. Journal of Game Development, vol. 1, issue 1, 2004, pp. 7-28.
- Kring A., Champandard A., Samarin N. DHPA* and SHPA*: Efficient Hierarchical Pathfinding in Dynamic and Static Game Worlds. Proc. Sixth Artificial Intelligence and Interactive Digital Entertainment Conference, 2010, pp. 39-44.
- Harabor D., Grastien A. Online Graph Pruning for Pathfinding On Grid Maps. AAAI Conf. Artif. Intell., 2011, pp. 1114-1119.
- Koenig S., Likhachev M., Furcy D. Lifelong Planning A*. Artif. Intell., vol. 155, № 1-2, 2004, pp. 93-146.
- Stentz A. The Focussed D* Algorithm for Real-Time Replanning. Proceeding IJCAI'95 Proceedings of the 14th international joint conference on Artificial intelligence -Volume 2, 1995, pp. 1652-1659.
- Koenig S., Likhachev M. D* Lite. Proceedings of the AAAI Conference of Artificial Intelligence (AAAI), 2002, pp. 476-483.
- Koenig S., Likhachev M. Fast Replanning for Navigation in Unknown Terrain. IEEE Trans. Robot., vol. 21, issue 3, 2005, pp. 354-363.
- Khatib O. Real time obstacle avoidance for manipulators and mobile robots. International Journal of Robotics and Research, vol. 5, № 1, 1986, pp. 90-98.
- Barraquand J., Latombe J.C. A Monte-Carlo algorithm for path planning with many degrees of freedom. Proceedings 1990 IEEE International Conference on Robotics and Automation, vol.3, 1990, pp. 1712-1717.
- Barraquand J., Latombe J.C. Robot motion planning: A distributed representation approach. International Journal of Robotics Research, vol. 10, issue 6, 1991. pp. 628 -649
- Kavraki L.E., Svestka P., Latombe J.C., Overmars M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom., vol. 12, № 4, 1996, pp. 566-580.
- Hsu D., Latombe J.C., Motwani R. Path Planning in Expansive Configuration Spaces. Proceedings 1997 IEEE International Conference on Robotics and Automation, vol. 3, 1997, pp. 2719-2726.
- LaValle S.M., Kuffner J.J. Rapidly-exploring random trees: Progress and prospects. 2000 Workshop on the Algorithmic Foundations of Robotics, 2000, pp. 293-308.
- Ferre E., Laumond J.-P. An iterative diffusion algorithm for part disassembly. Proceedings 2004 IEEE International Conference on Robotics and Automation, vol. 3, 2004, pp. 3149-3154.
- Bayazit O.B., Lien J.-M., Amato N.M. Probabilistic Roadmap Motion Planning for Deformable Objects. Proceedings 2002 IEEE International Conference on Robotics and Automation, vol. 2, 2002, pp. 2126-2133.
- Guibas L.J., Holleman C., Kavraki L.E. A Probabilistic Roadmap Planner for Flexible Objects with aWorkspace Medial-Axis-Based Sampling Approach. IEEE/RSJ Int. Conf. Intelligent Robot. Syst., 1999, pp. 254-260.
- Berenson D., Srinivasa S., Kuffner J.J. Task Space Regions: A framework for pose-constrained manipulation planning. Int. J. Rob. Res., vol. 30, № 12, 2011, pp. 1435-1460.
- Yakey J.H., LaValle S.M., Kavraki L.E. Randomized path planning for linkages with closed kinematic chains. IEEE Trans. Robot. Autom., vol. 17, № 6, 2001, pp. 951-958.
- LaValle S.M., Kuffner J.J. Randomized Kinodynamic Planning. Int. J. Rob. Res., vol. 20, № 5, 2001, pp. 378-400.
- Niederreiter H. Random number generation and Quasi-Monte Carlo methods. Society for Industrial and Applied Mathematics, 1992, 241 p.
- Dmitriev K.A. From Monte Carlo to Monte Carlo Quasi. International Conference GraphiCon2002, 2002, pp. 53-59.
- Sobol' I.M. Multidimensional quadrature formulas and Haar functions. M.: Home edition of Physical and Mathematical literature, Publishing house "Science", 1969, 288 p..
- Sobol' I.M. Numerical Monte Carlo methods. M.: Home edition of Physical and Mathematical literature, Publishing house "Science", 1973, 312 p..
- Khaksar W., Hong T.S., Khaksar M., Motlagh O. A low dispersion probabilistic roadmaps (LD-PRM) algorithm for fast and efficient sampling-based motion planning. Int. J. Adv. Robot. Syst.vol. 10, № 397, 2013, pp. 1-10.
- LaValle S.M., Branicky M.S. On the Relationship Between Classical Grid Search and Probabilistic Roadmaps. In Algorithmic Foundations of Robotics V. Springer Tracts in Advanced Robotics, vol. 7, 2004, pp. 59-75
- Zhang L., Kim Y.J., Manocha D. C-DIST: efficient distance computation for rigid and articulated models in configuration space. Proc. 2007 ACM Symp. Solid Phys. Model. -SPM ’07, 2007, pp. 159-169.
- Lin M.C. Efficient Collision Detection for Animation and Robotics. Ph.D. thesis, Department of Electrical Engineering and Computer Science, University of California, Berkeley, USA, 1993, 159 p.
- Christer Ericson. Real-time Collision Detection. The Morgan Kaufmann Series in Interactive 3-D Technology. CRC Press, 2004, 632 p.
- Andersen K. A., Bay C. A survey of algorithms for construction of optimal Heterogeneous Bounding Volume Hierarchies. Technical Report. Copenhague, Denmark: Department of Computer Science, University of Copenhagen, 2006, 32 p.
- Zolotov V.A., Semenov V.A. Advanced indexing methods for large multidimensional data in complex dynamic scenes. Trudy ISP RAN/Proc. ISP RAS, vol. 24, 2013, pp. 381-416 DOI: 10.15514/ISPRAS-2013-24-17
- Zolotov V.A., Semenov V.A. Trudy ISP RAN/Proc. ISP RAS, vol. 26, issue 2, 2014, pp. 175-196 DOI: 10.15514/ISPRAS-2014-26(2)-9
- Zolotov V.A., S. P.K., Semenov V.A. Octree-based approach to spatial indexing of complex dynamic scenes. International Conference GraphiCon2015, Russia, 2015, pp. 115-122.
- Pungotra H. Collision Detection and Merging of Deformable B-spline Surfaces in Virtual Reality Environment. Ph. D. thesis, The Univeristy of Western Ontario, Canada, 2010, 180 p.
- Sandqvist J., Collision detection using boundary representation, BREP. Master thesis, Umeå University, Sweden, 2015, 54 p.
- Su C.J., Lin F., Ye L. New collision detection method for CSG-represented objects in virtual manufacturing. Computers in Industry, vol. 40, № 1, 1999, pp. 1-13.
- Klein J., Zachmann G. Point cloud collision detection. Proc. Eurographics 2004, 2004, pp. 567-576.
- Schwarzer F., Saha M., Latombe J.C. Exact Collision Checking of Robot Paths. In Algorithmic Foundations of Robotics V. Springer Tracts in Advanced Robotics, vol. 7, 2004, pp. 25-41.
- Yershova A., LaValle S.M. Improving Motion Planning Alorithms by Efficient Nearest-Neighbor Searching. IEEE Transactions on Robotics, vol. 23, issue 1, 2007, pp. 151-157.
- Yershova A., LaValle S.M. Planning for closed chains without inverse kinematics. Department of Computer Science, University of Illinois, Urbana, USA, 2007, 7 p. Available at http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.115.7831&rep=rep1&type=pdf.
- Brown R.A. Building a Balanced k-d Tree in O (kn log n) Time. J. Comput. Graph. Tech, vol. 4, № 1, 2015, pp. 50-68.
- Ciaccia P., Patella M., Rabitti F., Zezula P. Indexing Metric Spaces with M-Tree. Proc. Atti del Quinto Convegno Nazionale SEBD, 1997, pp. 67-86.
- Gipson B., Moll M., Kavraki L.E. Resolution Independent Density Estimation for motion planning in high-dimensional spaces. Proc. 2003 IEEE International Conference on Robotics and Automation, 2013, pp. 2437-2443.
- Fredriksson K. Geometric Near-neighbor Access Tree (GNAT) revisited. arXiv:1605.05944v2, 2016, 7 p.
- Yu C., Ooi B.C., Tan K.-L. Indexing the Distance: An Efficient Method to KNN Processing. Proceedings of the 27th International Conference on Very Large Data Bases, 2001, pp. 421-430.
- Beygelzimer A., Kakade S., Langford J. Cover trees for nearest neighbor. ICML ’06, Proc. 23rd Int. Conf. Mach. Learn., 2006, pp. 97-104.
- Ichnowski J., Alterovitz R. Fast Nearest Neighbor Search in SE (3) for Sampling-Based Motion Planning. Algorithmic Foundations of Robotics XI, Volume 107 of the series Springer Tracts in Advanced Robotics, 2015, pp 197-214.
- Amato N.M., Bayazit O.B., Dale L.K., Jones C., Vallejo D. Choosing good distance metrics and local planners for probabilistic roadmap methods. IEEE Trans. Robot. Autom., vol. 16, № 4, 2000, pp. 442-447.
- Nissoux C., Simeon T., Laumond J.-P. Visibility based probabilistic roadmaps. 1999 IEEE/RSJ Int. Conf. Intell. Robot. Syst., vol. 3, 1999, pp. 1316-1321.
- Amato N.M., Wu Y. A randomized roadmap method for path and manipulation planning. Proc. 1996 IEEE International Conference on Robotics and Automation, vol. 1, 1996, pp. 113-120.
- Amato N.M., Bayazit O.B., Dale L.K., Jones C., Vallejo D. OBPRM: An Obstacle-Based PRM for 3D Workspaces. Proceeding WAFR '98 Proceedings of the third workshop on the algorithmic foundations of robotics on Robotics: the algorithmic perspective, 1998, pp. 155-168.
- Yeh H.Y., Thomas S., Eppstein D., Amato N.M. UOBPRM: A uniformly distributed obstacle-based PRM. IEEE Int. Conf. Intell. Robot. Syst., 2012, pp. 2655-2662.
- Hsu D., Jiang T., Reif J., Sun Z. The bridge test for sampling narrow passages with probabilistic roadmap planners. Proc. 2003 IEEE International Conference on Robotics and Automation, vol. 3, 2003, pp. 4420-4426.
- Boor V., Overmars M.H., Stappen A. F. Van Der. The Gaussian sampling strategy for probabilistic roadmap planners. Proc. 1999 IEEE International Conference on Robotics and Automation, vol 2, 1999, pp. 1018-1023.
- Lien J.-M., Thomas S., Amato N.M. A general framework for sampling on the medial axis of the free space. Proc. 2003 IEEE International Conference on Robotics and Automation, vol. 3, 2003, pp. 4439-4444.
- Wilmarth S. A., Amato N.M., Stiller P.F. MAPRM: a probabilistic roadmap planner with sampling on the medial\naxis of the free space. Proc. 1999 IEEE International Conference on Robotics and Automation, vol 2, 1999, pp. 1024-1031.
- Holleman C., Kavraki L.E. A framework for using the workspace medial axis in PRM planners. Proc. 2000 IEEE International Conference on Robotics and Automation, vol 2, 2000, pp. 1408-1413.
- Nielsen C.L.L., Kavraki L.E. A two level fuzzy PRM for manipulation planning. 2000 IEEE/RSJ Int. Conf. Intell. Robot. Syst., vol. 3, 2000, pp. 1716-1721.
- Bohlin R., Kavraki L.E. Path planning using lazy PRM. Proc. 2000 ICRA Millenn. Proc. 2000 IEEE International Conference on Robotics and Automation, vol 1, 2000, pp. 521-528.
- Bohlin R., Kavraki L.E. A Randomized Approach to Robot Path Planning Based on Lazy Evaluation. In Handbook of Randomized Computing, volume I/II, Springer, 2001, pp. 221-253.
- Leven P., Seth H. Toward Real-Time Path Planning in Changing Environments. Proceedings of the Fourth International Workshop on the Algorithmic Foundations of Robotics, 2000, pp. 363-376.
- Nieuwenhuisen D., Van Den Berg J., Overmars M.H. Efficient path planning in changing environments. 2007 IEEE/RSJ Int. Conf. Intell. Robot. Syst., 2007, pp. 3295-3301.
- Jaillet L., Simeon T. A PRM-based motion planner for dynamically changing environments. 2004 IEEE/RSJ Int. Conf. Intell. Robot. Syst., vol. 2, 2004, pp. 1606-1611.
- Bessiere P., Ahuactzin J.M., Talbi E.-G., Mazer E. The Ariadne’s Clew Algorithm: Global Planning With Local Methods. Proceeding of the Workshop on Algorithmic Foundations of Robotics, 1995, pp. 39-49.
- Mazer E., Ahuactzin J.M., Bessiere P. The Ariadne ’ s Clew Algorithm. Journal of Artifical Intelligence Research, vol. 9, 1998, pp. 295-316.
- Carpin S., Pillonetto G. Motion planning using adaptive random walks. IEEE Trans. Robot., vol. 21, № 1, 2005, pp. 543-548.
- Carpin S., Pillonetto G. Merging the adaptive random walks planner with the randomized potential field planner. Proc. Fifth Int. Work. Robot Motion Control, 2005, pp. 151-156.
- Sanchez G., Latombe J.C. A single-query bi-directional probabilistic roadmap planner with lazy collision checking. In Robotics Research, Volume 6 of the series Springer Tracts in Advanced Robotics, Springer, 2003, pp 403-417.
- Hsu D. Randomized Single-query Motion Planning in Expansive Spaces. Ph. D. thesis, Stanford University, USA, 2000, 118 p.
- Sagan H. Space-Filling Curves. Springer-Verlag, New York, 1994, 193 p.
- Kuffner J.J., LaValle S.M. RRT-connect: An efficient approach to single-query path planning. Proc. 2000 IEEE International Conference on Robotics and Automation, vol 2, 2000, pp. 995-1001.
- Bekris K.E., Chen B.Y., Ladd A.M., Plaku E., Kavraki L.E. Multiple Query Motion Planning using Single Query Primitives. IEEE/RSJ Int. Conf. Intell. Robot. Syst., 2003, pp. 656-661.
- Plaku E., Kavraki L.E. Distributed Sampling-Based Roadmap of Trees for Large-Scale Motion Planning. Proc. 2005 IEEE International Conference on Robotics and Automation, 2005, pp. 3879-3884.
- Strandberg M. Robot Path Planning: An Object-Oriented Approach. Ph.D.thesis, Automatic and Control Departmentof, Signals, Sensors and Systems Royal Institute of Technology (KTH), Stockholm, Sweden, 2004, 244 p.
- Bruce J.R., Veloso M. Real-time multi-robot motion planning with safe dynamics. Multi-Robot Systems. From Swarms to Intelligent Automata, Volume III. Proceedings from the 2005 International Workshop on Multi-Robot Systems, Springer, 2005, pp. 1-12.
- Bruce J.R. Real-time motion planning and safe navigation in dynamic multi-robot environments. PhD. Thesis, Carnegie Mellon University, Pittsburgh, USA, 2006, 204 p.
- Yershova A., Jaillet L., Siméon T., LaValle S.M. Dynamic-Domain RRTs: Efficient Exploration by Controlling the Sampling Domain. Proc. 2005 IEEE International Conference on Robotics and Automation, 2005, pp. 3856-3861.
- Raveh B., Enosh A., Halperin D. A little more, a lot better: Improving path quality by a path-merging algorithm. IEEE Trans. Robot., vol. 27, № 2, 2011, pp. 365-371.
- Urmson C., Simmons R. Approaches for heuristically biasing RRT growth. Proc. 2003 IEEE/RSJ Int. Conf. Intell. Robot. Syst., vol.2, 2003, pp. 1178-1183.
- Jaillet L., Cortes J., Simeon T. Sampling-Based Path Planning on Costmaps Configuration-space. Ieee Trans. Robot., vol. 26, № 4, 2010, pp. 635-646.
- Hauser K. Lazy collision checking in asymptotically-optimal motion planning. Proc. 2015 IEEE International Conference on Robotics and Automation, 2015, pp. 2951-2957.
- Luo J., Hauser K. An Empirical Study of Optimal Motion Planning. IEEE/RSJ Conf. Intell. Robot. Syst., 2014, pp. 1761-1768.
- Marble J.D., Bekris K.E. Asymptotically Near-Optimal is Good Enough for Motion Planning. 15th Int. Symp. Robot. Res., 2011, pp. 419-436.
- Marble J.D., Bekris K.E. Computing spanners of asymptotically optimal probabilistic roadmaps. IEEE/RSJ Int. Conf. Intell. Robot. Syst., 2011, pp. 4292-4298.
- Marble J.D., Bekris K.E. Towards small asymptotically near-optimal roadmaps. Proc. 2012 IEEE International Conference on Robotics and Automation, 2012, pp. 2557-2562.
- Dobson A., Bekris K.E. Improving Sparse Roadmap Spanners. Proc. 2013 IEEE International Conference on Robotics and Automation, 2013, pp. 4106-4111.
- Dobson A., Bekris K.E. Sparse roadmap spanners for asymptotically near-optimal motion planning. Int. J. Rob. Res., vol. 33, № 1, 2014, pp. 18-47.
- Nasir J., Islam F., Malik U., Ayaz Y., Hasan O., Khan M., Muhammad M.S. RRT*-SMART: A rapid convergence implementation of RRT*. Int. J. Adv. Robot. Syst., vol. 10, 2013, pp. 1-12.
- Arslan O., Tsiotras P. Use of relaxation methods in sampling-based algorithms for optimal motion planning. Proc. 2013 IEEE International Conference on Robotics and Automation, 2013, pp. 2421-2428.
- Janson L., Pavone M. Fast Marching Trees: a Fast Marching Sampling-Based Method for Optimal Motion Planning in Many Dimensions -Extended Version, arXiv:1306.3532v4, 2013, pp. 1-60.
- Salzman O., Halperin D. Asymptotically near-optimal RRT for fast, high-quality, motion planning. Proc. 2014 IEEE International Conference on Robotics and Automation, 2014, pp. 4680-4685.
- Devaurs D., Simeon T., Cortes J. Optimal Path Planning in Complex Cost Spaces with Sampling-Based Algorithms. IEEE Trans. Autom. Sci. Eng., vol. 13, № 2, 2016, pp. 415-424.
- Klemm S., Oberlander J., Hermann A., Roennau A., Schamm T., Zollner J.M., Dillmann R. RRT∗-Connect: Faster, asymptotically optimal motion planning. 2015 IEEE Int. Conf. Robot. Biomimetics, 2015, pp. 1670-1677.
- Starek J.A., Gomez J. V, Schmerling E., Janson L., Moreno Luis, Pavone M. An Asymptotically-Optimal Sampling-Based Algorithm for Bi-directional Motion Planning. IEEE/RSJ Int. Conf. Intell. Robot. Syst., 2013, pp. 2015.


