Обзор свойств клеточных автоматов, их применения

Клеточные автоматы, впервые предложенные в качестве эффективных дискретных моделей одним из основоположников современных компьютерных технологий Дж. фон Нейманом в 40-е годы прошлого века, приобрели особую популярность начиная с 90-х годов после публикации монографии «Машины клеточных автоматов» [11] и в настоящее время широко используются в компьютерных науках, математике, физике, теоретической биологии и микромеханике. Многие сложные явления, такие как, развитие, рост, самовоспроизведение, морфогенез описываются сложными дифференци-

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №1, 2017 год альными уравнениями и поэтому построение моделей на основе этих уравнений очень затруднительно. Однако эти процессы можно описать с помощью клеточных автоматов, что очень сильно упрощает процесс моделирования. На данный момент на основе клеточных автоматов строятся модели организации человеческого мозга и всей физической Вселенной. В настоящее время клеточные автоматы приобрели актуальность с бурным ростом параллельных вычислений, так как они обладают большим потенциалом параллелизма. Поэтому все больше и больше появляется разнообразных моделей основанных на концепции клеточных автоматов.

Понятие клеточного автомата

Данный термин был введен впервые американским математиком Дж. фон Нейманом в теории игр автоматов. Он возник при пытке смоделировать процесс самовоспроизведения биологических систем в 1966 году, с помощью абстрактных динамических систем. Данные системы и получили название клеточные автоматы.

Клеточные автоматы – дискретная динамическая система, состоящая из совокупности одинаковых клеток, соединенных между собой одинаковым образом. Все клетки образуют решетку клеточного автомата . Решетки бывают разнообразных типов, отличающиеся между собой как по форме, так и по размерности клеток. Каждая отдельная клетка находится в определенном состоянии, которое изменяется с течением времени, в зависимости от состояния своих соседей и, в зависимости от типа автомата, собственного состояния. Совокупность всех состояний клеток решетки определяют состояние решетки . Клетки могут располагаться на одномерной прямой, плоскости или в многомерном пространстве. Всякой клетке присуще заданное количество «соседей», зависящее от вида используемой клетки. Соседи устанавливаются или по наличию общих границ у клеток, или с помощью графа. Данные клетки образуют окрестности клетки . Различают два вида окрестности: окрестность Неймана (см. рис. 1), она состоит из четырех соседних клеток; окрестность Мура (см. рис. 2), она состоит из восьми соседних клеток.

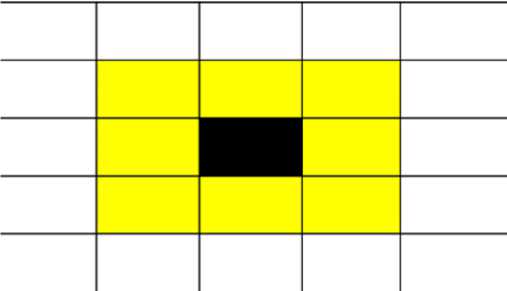
Рис. 1. Окрестность Неймана

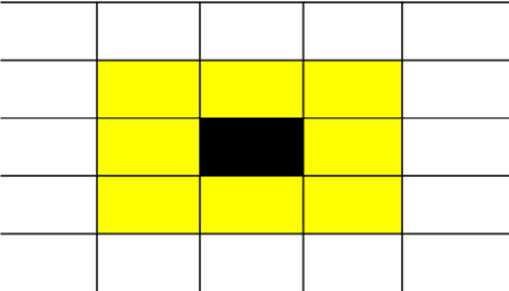
Рис. 2. Окрестность Мура

Состояние клетки в следующий момент времени задается как функция от ее собственного состояния и состояний соседей в текущий момент времени. Вид этой функции определяет поведение клеточного автомата. Если новое состояние клетки зависит от текущего её состояния, то о соответствующем клеточном автомате говорят, что он является автоматом с клетками с памятью , иначе- автоматом с клетками без памяти . Время в системе изменяется дискретно, так за тактом. За один такт изменяется состояние решетки, называемый итерацией.

Главными достоинствами клеточного автомата являются следующие правила:

• -    способность элементов к пространственному перемещению и применение понятия состояния к новому положению;

• -    состояние каждой клетки обновляется в результате выполнения последовательности дискретных постоянных шагов во времени;

• -    переменные в каждой клетке изменяются одновременно («синхронно»), исходя из значений переменных на предыдущем шаге;

• -    правило определения нового состояния клетки зависит только от ее локальных значений из некоторой окрестности данной клетки [1-3].

Однако на практике при решении некоторых видов задач приходится отказываться от некоторых приведенных выше правил. При этом полученные автоматы продолжают относиться к классу клеточных.

На первый взгляд, клеточные автоматы являются очень простыми. Тем не менее, эта простая структура, когда она повторяется несколько раз, производит сложные схемы, отображающие имитацию различных природных систем.

Формальное описание клеточного автомата

Клеточный автомат A представляет собой следующий набор объектов { G , Z , Nf }, где:

• -    G - дискретное метрическое пространство, то есть решетка автомата. Оно гарантирует, что все клетки окрестности расположены на конечном расстоянии от данной. Как правило пространство G бывает одно-, двух-, трехмерным или бывает больших размерностей;

• -    Z - конечное множество возможных состояний клеток. Отсюда следует, что состояние решетки является элементом множества Z^;

• -    N - конечное множество, определяющее окрестность клетки, то есть, те | N | клеток, которые влияют на новое состояние данной;

• -    f - правила автомата. Они представляют собой вычислимую программу, которая, используя |N |+1 аргумент для автомата с клетками с памятью и |N| аргументов для автомата с клетками без памяти, позволяет вычислять новое состояние данной клетки. Иногда правила могут быть записаны, как логическая или математическая функция переходов, действующая Z X Z ^lNl -^ Z для автомата с клетками с памятью и Z ^lNl ^ Z для автомата с клетками без памяти.

Автомат, определённый таким образом, обладает всеми свойствами классических клеточных автоматов, перечисленными выше.

Классификация клеточных автоматов

По изменению состояния клетки

• -    детерминированные - состояние клетки в последующий момент времени однозначно определяется ее внутренним состоянием и состоянием ее ближайших соседей в предыдущий момент времени. Состояние данной клетки в следующий момент времени является однозначной функцией от двух переменных - состояния этой клетки и суммы состояний ее ближайших соседей в предшествующий момент времени. При таком определении клеточный автомат не обладает па-

• мятью. Также они еще называются простыми или классическими. Для того, чтобы клеточный автомат был с памятью, необходимо предположить, что функция зависит, например, также от состояния клетки еще в более ранний момент времени;

• -    подвижные клеточные автоматы - характеризуются возможностью изменения положения клетки в решетке во время эволюции системы;

• -    неподвижные клеточные автоматы - положение клетки во время эволюции остается постоянным. Иногда используются правила, записанные в виде обыкновенных дифференциальных уравнений. В этом случае состояния клеток задаются набором переменных, значения которых способны принимать любые действительные числа;

• -    вероятностные - клеточные автоматы, в которых состояние клеток в последующий момент времени определяется на основе некоторых вероятностей. В таких автоматах при имитации или компьютерном эксперименте некоего процесса, для каждой клетки датчиком случайных чисел генерируется случайное число в (0 < в < 1 ), которое сравнивается с вероятностью W возникновения этого процесса. Если в < W, то происходит наступление данного процесса . В данных автоматах вместо функции изменения состояния необходимо задать набор вероятностей изменения состояния клетки, которые показывают, какой будет вероятность перехода клетки из состояния в данный момент времени, в состояние в последующий момент времени при условии, что состояния его ближайших соседей в данный момент времени принимали определенные значения.

Классификация решеток клеточных автоматов и агентов

Рассматривая клеточные автоматы с двумерными решетками из правильных многоугольников, возможны только три вида таких решеток, а, следовательно, и видов агентов: треугольная (см. рис. 3), квадратная (см. рис. 4), гексагональная (см. рис. 5). Других решеток кроме этих не существует.

Треугольная решетка имеет окрестность Неймана, состоящую из трех клеток. Данные клетки называются главными соседями, так как они имеют общую сторону с клеткой. Так же присутствует окрестность Мура, в нее включены все клетки закрашенные желтым на рисунке 3.

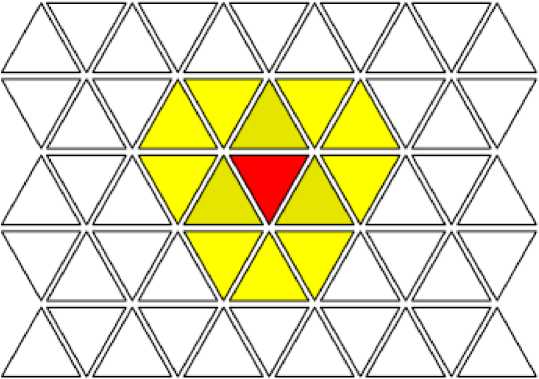
Рис. 1. Треугольная решетка клеточного автомата

На квадратной решетке у любой клетка по восемь соседей, четыре из которых составляют окрестность Неймана.

Рис. 2. Квадратная решетка клеточного автомата

У гексагональной клетки все соседи входят в окрестность Неймана.

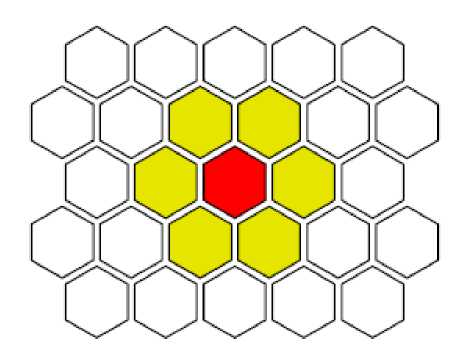
Рис. 3. Гексагональная решётка клеточного автомата

Сферы применения клеточных автоматов

Клеточные автоматы предоставляют большую свободу в выборе структуры и правил развития системы. Тем самым область применения их почти безгранична: от простых игр, например, «крестики-нолики», до систем искусственного интеллекта. Данная тема очень актуальна в настоящая время, так как клеточные автоматы являются универсальным инструментом анализа и моделирования. С помощью них могут быть решены многие вопросы в окружающем мире. Создатель игры «Жизнь» Конуэй, применил клеточный автомат для подтверждения теории зарождения жизни на Земле: предположим себе достаточно большое количество «первичного бульона» из хаотически распределенных клеток, если можно ожидать появления из такого хауса структур, способных самовоспроизводить себя, то это и есть подтверждение.

Моделирование и имитация

Клеточные автоматы, реализованные на компьютере, могут быть использованы для моделирования широкого спектра сложных биологических, физических, социальных, информационных систем [5]. Хотя многие природные системы, например, турбулентность в жидкостях или образование снежинок могут быть проанализированы с использованием традиционных математических моделей, таких как дифференциальные уравнения, клеточные автоматы часто обеспечивают более простой инструмент, который сохраняет суть процесса, с помощью которого сложные природные явления возникают. Согласно Вольфраму [6], клеточные автоматы по своей природе более эффективны при анализе многих естественных систем, чем традиционные вычислительные методы, поскольку механизмы, найденные в большинстве природных систем ближе к клеточным автоматам, чем при использовании обычных вычислений.

Сложные глобальные структуры и поведение массива клеточных автоматов возникают из простых законов. Таким образом, клеточные автоматы особенно хорошо подходят для моделирования любой системы, которая состоит из простых компонентов, где глобальное поведение системы зависит от поведения и локальных взаимодействий отдельных компонентов. Ниже приведены некоторые конкретные примеры биологических и физических систем, которые были эффективно смоделированы с использованием клеточных автоматов:

• -    поведение газа;

• -    ферромагнетизм;

• -    распространение огня в лесу;

• -    развитие города;

• -    турбулентность в жидкостях;

• -    иммунология и биологическое старение;

• -    поток электричества в энергосистеме;

• -    кристаллизация;

• -    описание движения толпы;

• -    модель «хищник-жертва».

Клеточные автоматы являются идеальным инструментом для компьютерного моделирования жизни, потому что они аналогичны жизни коренным образом. А именно, клеточные автоматы основаны на простых правилах, из которых состоит сложная жизнь, например, поведение, в том числе может возникнуть и самовоспроизводство при правильных условиях.

Криптография и генератор случайных чисел

Клеточные автоматы могут служить в качестве источника случайных чисел, которые используются для шифрования сообщений, запуска моделирования, а также для других целей.

Согласно Саркару [7], конфигурации из последовательности поколений клеточных автоматов могут быть использованы в качестве случайной последовательности. Для этой цели обычно используются одномерные клеточные автоматы. Саркар приводит несколько конкретных приложений, которые генерируют случайные числа с помощью клеточных автоматов, в том числе закрытых ключей криптосистем, открытых ключей криптосистемы и хэш-функций.

Вольфрам [8] также говорит о том, что генератор случайных чисел, используемый для больших чисел в его системе Mathematica , основана на элементарном клеточном автомате, известным как «Правило 30».

Реализация параллельных компьютеров

Клеточные автоматы обладают свойством универсального вычисления, что означает, что они в принципе могут выполнять любые вычисления. Это свойство может позволить на основе клеточных автоматов сформировать архитектурную модель для построения компьютеров на основе параллельных вычислений. Например, можно было бы изготовить на одном кристалле кремния вычислительно-универсальный клеточный автомат с около миллиона клеток и временным шагом около одной миллиардной секунды. Однородность клеточных автоматов позволило бы им быть легко реализованными с помощью интегральных схем. А однородная, одномерная структура клеточных автоматов позволило относительно просто находить дефекты.

Создание мультимедийного контента

Одним из очевидных применений клеточных автоматов являются генерация сложных и часто красивых узоры (см. рис. 6). Согласно Боттони, Камилли и Фарали [9], клеточные автоматы могут быть использованы компьютерными художниками для создания визуальных или акустических моделей для искусства или презентаций. Буттони и др. создали приложение, известное как ExcapeMe , которое может быть использовано компьютерными художниками, исследователями и студентами для изучения динамики клеточных автоматов при генерации мультимедийного контента.

Рис. 6. Узоры, сгенерированные с помощью клеточного автомата

Возможности построения клеточных автоматов на основе нечеткой логики и нечетких множеств

Главная цель клеточных автоматов состоит в том, чтобы построенные модели были основаны на поведении реальных систем. Много хороших моделей было разработано, как показано выше. Данные примеры клеточных автоматов базируются на основе классической двузначной логики. Однако в реальном мире существует много неопределенных аспектов, проблемы неточности и неопределенности данных. Существуют задачи, когда предметная область описывается экспертом лингвистическими (словесными) правилами, то есть в системе преобладают качественные характеристики; когда трудно разработать достаточно простую математическую модель предметной области и необходима высокая гибкость в настройках системы управления. И здесь на помощь в решении таких задач может прийти аппарат нечеткой логики и нечетких множеств, расширяющий возможности классической логики.

Нечеткая логика дает возможность непрерывного анализа между «ложью» и «истиной» и ликвидирует разрыв между качественным и количественным моделированием. Она была первоначально предложена Заде как обобщение двоичной логики и используется для моделирования неточностей, неясности и неопределенности в реальном мире. Нечеткая логика не отвечает двоичному свойству дихотомии; следовательно, нечеткие переменные могут состоять из частично перекрывающихся нечетких множеств. Когда нечеткое множество предназначено для управления количественной (числовой) информацией, она полностью описывается функцией принадлежности, которая возвращает значение принадлежности (μ) в пределах [0,1] для данного объекта в нечетком множестве. Для каждого нечеткого множества, используется лингвистическая переменная описывающие его качества. Лингвистические переменные, помимо описания примитивных нечетких множеств, также используются для определения новых наборов, основанных на примитивных. Это достигается за счет применения модификаторов, которые являются словесными определениями, такими как «более или менее», «не», «очень» и т.д. Каждый модификатор соединяется с числовым выражением, которое применяется к функции принадлежности примитивного набора. Лингвистика в нечеткой логике, позволяют управлять информацией, в некотором смысле, ближе к человеческому пониманию.

База знаний представляется как правила «Если ... то», соединяя гипотезы с выводами через фактор определенности. Наиболее часто используемыми моделями логического вывода являются Мам-дани и подход Сугено.

Сегодня нечеткая логика распространена в качестве одного из методов, которые обычно используются для управления производственными процессами, особенно для контроля качества продукции и затрат. Например, для управления сушильной печью при производстве цемента, потому что в этом процессе должно быть учтено большое количество переменных и, в частности, климатические воздействие на сушильную печь высотой несколько десятков метров. В автомобильной промышленности благодаря применению методов нечеткой логики появилось автоматическое переключение передач в трансмиссии, системы впрыска, шумоподавляющие системы и кондиционеры воздуха. Большое количество электротехнических и электронных приложений доступно широкой публике, особенно в Японии. Например, компактные портативные цифровые видеокамеры, обладающие повышенной чувствительностью к перемещениям. В данных устройствах нечеткая логика управляет системой стабилизации изображения.

Рассмотрев данные примеры, можно сделать вывод, что данные методы имеют место применяться при построении клеточных автоматов.

Исследуем возможность применения нечеткой логики и теории нечетких множеств при построении клеточного автомата для решения задачи моделирования распространения лесного пожара.

Пожары являются одним из самых распространенных экологических катастроф, которые влияют на флору, фауну и ставят под угрозу человеческие жизни. Построение данной модели позволит обеспечить надежное прогнозирование распространения огня, с целью оказания помощи при работе пожарных, предотвращения опасности для окружающей среды и избежание потерь людских и экономических.

Распространение лесных пожаров представляет собой сложный пространственный и временной динамический процесс, который зависит от большого числа неопределенных и неточных факторов, таких как скорость ветра, уклон местности, тип растительности, влажность и т.д.

Данный процесс сложно реализовать с помощью классического клеточного автомата, так как есть трудности учета значительных неопределенностей (описанных выше), которые характеризуют входные данные и внутренние параметры уравнений модели. Это происходит во многих случаях в зависимости от конкретных параметров среды на местности.

Для преодоления этих трудностей возможно применить нечеткую логику и теорию нечетких множеств при построении клеточного автомата для использования нечеткости в правилах для определения состояний клеток клеточного автомата.

Клеточный автомат на основе нечеткой логики характеризуется следующими свойствами:

• -    дискретным метрическим пространством;

• -    конечным множеством, определяющего окрестность клетки, то есть, клеток, которые влияют на новое состояние;

• -    множеством конечных состояний клетки;

• -    функцией перехода TF , которая вычисляет состояние каждой клетки на шаге (t + 1) в зависимости от состояния его соседних клеток в момент времени t.

Будущая модель включает в себя параметры, связанные со следующими экологическими аспектами:

• -    рельеф местности;

• -    ветер (скорость и направление);

• -    характеристики растительности, в том числе влияние погодных условий (влажность, температура и осадки).

Как уже упоминалось ранее, в реальных жизненных ситуациях, данные предоставляемые для указанных выше характеристик являются неточными и расплывчатыми, что приводит к ненадежности в результатах моделирования распространения пожара.

Более конкретно, предлагаемая модель распространения лесного пожара основывается в двумерном пространстве, в то время как, конечным множеством было выбрано окрестность Мура, чтобы обеспечить достаточное разнообразие распространения пожара. Каждая клетка автомата может находится в одном из состояний, которое связано с лингвистической переменной уровня пожара . Можно использовать следующие пять состояний:

• 5 = {Нет пожара(НеП), Небольшой пожар (НП), Средний пожар (СП),

Большой пожар(БП) , Сожжено(С) }                                     (1)

Кроме того, можно ввести дополнительное состояние, в котором клетка не содержит воспламеняющих элементов и, следовательно, клетки в данном состоянии не будут использоваться в процессе вычислений (например, дороги в лесу, горы, поля).

Используя нечеткий подход [10], для представления уровня пожара, каждой клетки ставится числовое значение cell.state , которое может одновременно соответствовать, с различной степенью принадлежности, к различным лингвистическим состояниям среди тех, которые перечислены в (1). Таким образом, для того, чтобы применить нечеткие правила нам понадобится процедура фаззифик-ции, которая числовое значение превращает в степень принадлежности для каждого из нечетких множеств выше.

Фаззификация осуществляется с помощью функции принадлежности μ ( cell.state ), для каждого элемента S , которая берет числовое значение клетки и возвращает принадлежность к лингвистическому состоянию на заранее определенной числовой шкале. При реализации лучше всего выбрать классическую треугольную форму функции принадлежности, она обладает приемлемой точностью и простотой построения.

В дополнение к нечеткому состоянию клетки, определяющего ее состояние пожара, каждая клетка может быть охарактеризована несколькими свойствами, представляющими соответствующие переменные среды в точке ландшафта, связанного с самой клеткой. Эти свойства используются в функции перехода клеточного автомата для того, чтобы смоделировать распространение пожара в неоднородном ландшафте. Например, каждая клетка (как писалось выше) будет характеризоваться направлением и интенсивностью ветра, максимальный уклоном местности, его направлением и типом растительности.

Распространение пожара определяется с помощью входных данных состояния восьми соседей (т.е. N, NW , W , SW , S , SE , E и NE) и текущего состояния клетки. Для каждого соседа применяются следующие лингвистические правила:

• 1.    Если соседняя клетка Средний пожар , то состояние клетки Небольшой пожар.

• 2.    Если соседняя клетка Большой пожар , то состояние клетки Средний пожар.

• 3.    Если соседняя клетка Сожжено , то состояние клетка Большой пожар.

Это будет достигаться благодаря учету за степенью принадлежности к различным нечеткими состояниям соседних клеток.

Помимо распространения пожара между соседними клетками, функция перехода изменяет внутреннее состояние уровня пожара клетки. С точки зрения лингвистических правил, это делается следующим образом:

• 1.    Если клетка в состоянии Нет пожара , то состояние клетки Нет пожара .

• 2.    Если состояние клетки Небольшой пожар , то состояние ячейки Средний пожар .

• 3.    Если состояние клетки Средний пожар , то состояние клетки Большой пожар .

• 4.    Если состояние клетки Большой пожар , то состояние ячейки Сожжено .

• 5.    Если состояние клеток Сожжено , то состояние клеток Сожжено .

Переходы между нечеткими состояниями будут управляться с помощью топливо-зависимых коэффициентов для каждого состояния из (1).

После применения нечетких правил, включенных в функции перехода клеточного автомата, необходимо использовать процесс дефаззификация для того, чтобы сохранить состояние пожара каждой клетки в качестве числового значения для следующего шага клеточного автомата.

Заключение

Рассмотрев концепцию клеточных автоматов можно с уверенностью сказать, что на их основе можно строить модели разнообразных процессов, относящихся к различным областям науки. Доказательством этого были приведенные в данной статье примеры. Важной особенностью клеточных автоматов является их простота использования и конфигурирования.

Возможность использование нечеткой логики, для построения клеточного автомата, принципиально упростит моделирование многих задач. Применение нечеткой логики позволит:

• -    учитывать нечеткие исходные данные: например, непрерывно изменяющиеся во времени значения (динамические задачи), значения, которые невозможно задать однозначно (результаты статистических опросов, рекламные компании и т.д.);

• -    формализовать критериев оценки и сравнения – за счет оперирования критериями «большинство», «возможно», «преимущественно» и т.д.;

• -    проводить качественные оценки как входных данных, так и выходных результатов: оперирование не только значениями данных, но и их степенью достоверности и ее распределением;

• -    учитывать опыт и знания экспертов в оценке качества происходящих процессов, когда невозможно осуществлять точные математические вычисления.

Построенные на основе нечеткой логики клеточные автоматы позволят решить ряд следующих задач: прогнозирования, распознавания образов, адаптивного управления, распространения (веществ, пожара и т.д.).