Оценивание геометрических признаков пространственной структуры кровеносных сосудов

Современная медицина является одной из самых высокотехнологичных отраслей научной и практической деятельности, важнейшая задача которой состоит в разработке новых эффективных методик ранней диагностики различных патологий. Несколько последних десятилетий характеризуются значительным прорывом в области технической оснащённости медицины. Компьютерный анализ изображений стал основным инструментом медицинских диагностических систем, позволяющим существенно повысить качество диагностики. Наиболее активно информационные технологии внедряются в офтальмологию и кардиологию. Исследования направлены на анализ изображений сосудов глазного дна и сердца. В обоих случаях изображения кровеносных сосудов несут важную диагностическую информацию. На основании исследования кровеносных сосудов врач не только делает выводы о состоянии органа, но и диагностирует общие системные заболевания, такие как сахарный диабет (СД), полицитемию, анемию, гипертоническую болезнь.

Глазное дно, которое является предметом исследования в офтальмологии, представляет собой сложный объект с высокой плотностью заполнения сосудами и со множеством разветвлений и изгибов. С патологии сосудов глазного дна начинаются такие заболевания, как диабетическая ретинопатия (ДР) [1] и гипертония [2], которые и далее сопровождаются изменениями структуры сосудистого русла. Оценка состояния микроцир-куляторного русла глазного дна используется также при лечении системного атеросклероза, инсульта, заболеваний почек и др. Особенно ценным представляется то, что диагностически значимую информацию о глазном дне можно получить с применением неинвазивных методик, без побочных эффектов. Доступность неинвазивного осмотра и визуализации делает сосуды глазного дна наиболее информативными для анализа локальной микроциркуляции и прогностически значимыми в плане оценки гемодинамики всего организма. В связи с этим накоплен большой опыт, фактический материал по изучению, разработке и внедрению в медицинскую практику методов исследований кровеносного русла, анализа изображений сосудов, установления связей между изменениями кровеносных систем и многочисленными видами заболеваний.

Сосудистая система сердца является предметом исследования в кардиологии. Она характеризуется малым количеством сосудов, и её необходимо рассматривать как трёхмерный объект, применять методы цифрового анализа с учётом особенностей трёхмерного изображения. Атеросклеротические поражения сосудов сердца являются основной причиной многих заболеваний (атеросклероз, гипертоническая болезнь, ишемическая болезнь сердца, инсульт).

Таким образом, в медицинской практике всестороннее исследование указанных сосудистых систем является актуальным для диагностики многих заболеваний человека [3]. Сосудистые патологии являются одной из ключевых проблем современной медицины. Несмотря на значительные успехи, достигнутые за последние десятилетия в диагностике и лечении сосудистых заболеваний, число больных с поражениями сосудистых систем продолжает увеличиваться ( Семёнова, Бранчевский, Водовозов и др. ).

В связи с тем, что эффективность лечения сосудистой патологии в значительной мере зависит от точности определения её стадий и степени тяжести, одним из основных направлений в профилактике и лечении этих заболеваний является совершенствование методов их дифференциальной диагностики, включая прогнозирование возникновения заболеваний и донозоло-гическую диагностику ( Гаврилова, Купеев и др.).

Российская школа физиологов и морфологов, изучающих циркуляцию кровеносных сосудов, придаёт большое значение геометрии сосудистого русла (Гай-кин, Александров, Шагал). Геометрические параметры сосудистого русла, по их мнению, не являются случайными, а отражают адаптационные механизмы сосудов к заболеваниям. Западная научно-практическая школа большее внимание уделяет количественному анализу динамических параметров кровотока: линейной и объёмной скорости кровотока. Этот подход и определяет развитие научного приборостроения в этой области (Blondal, Gilmore, Kotlar). Клиническое применение такого подхода количественного анализа течения крови ограничено двумя факторами: 1) сложная и дорогая технология и 2) большая неопределённость интерпретации измеренных результатов для клинических целей. Широкое внедрение компьютерной техники и разнообразных устройств ввода видеосигналов дало возможность проводить диагностику методами автоматизированного анализа цифровых изображений. Это позволяет повысить скорость и качество диагностики, получать объективные данные об исследуемом объекте.

В настоящее время преимущественно используется подход, основанный на анализе локального диаметра сосуда. Такой подход является ограниченным в понимании процесса развития многих заболеваний. Клинически важными показателями, которые вносят существенный вклад в оценку степени патологии и вероятности развития заболеваний, являются и другие статистические параметры: неравномерность диаметра (чёткообразные изменения вен, локальный спазм артерий), кривизна, извилистость сосудов и др. [3–12]. В связи с этим актуальна задача разработки принципиально нового метода диагностики, позволяющего избежать указанных недостатков, дополнить имеющиеся представления о механизмах развития таких заболеваний, как диабетическая ангиопатия, включающая микроангиопатию, связанную с изменениями сосудов глазного дна, и макроангиопатию, сопряжённую с атеросклеротическими процессами в сосудах сердца, и диагностировать её, начиная с самых ранних стадий. Актуальными задачами являются также разработка новых и эффективных интегральных показателей состояния сосудов на изображениях глазного дна и коронарных сосудов сердца, методов их оценивания, а также создания на их основе автоматизированных систем диагностики, которые позволят стандартизировать постановку диагноза, значительно сократить время обследования [13, 14]. Предлагается единый подход к анализу двух классов изображений: микроциркуляторного русла глаза и сосудистой системы сердца. Подход основан на оценивании совокупности геометрических параметров сосудов с целью их дальнейшего диагностического анализа.

1.    Математическая модель участка сосуда

Предложена математическая модель изображения кровеносных сосудов, основанная на разделении геометрических характеристик сосуда на локальные параметры, рассчитываемые непосредственно в процессе трассировки (прослеживания сосудов), и интегральные (глобальные) признаки, которые далее используются для формирования классификационных признаков [15].

Для формирования локальных признаков введём такие понятия, как характеристики трассы сосуда и конфигурации его границ, которые будем называть стенками сосуда:

xb = xb (t), yb = yb (t) Jxb (t) = x(t) - r(t) sin ф, xb = x2 (t), y 2b = yb (t) , [yb (t) = y (t) + r(t) cos ф.

Трассу определим параметрически заданием центральной линии y( t) и функции толщины сосуда r(t), определяемой расстоянием от трассы до границы вет- ви, отсчитываемым по перпендикуляру к трассе:

Y( t ) = ( x (t), y (t)), r = r(t ),0 < t < Lv, dy dt

* 0

где t – натуральный параметр, расстояние от начала трассы, измеренное по трассе; L_v – длина трассы.

Центральная линия сегмента сосуда представляет собой линию, образованную центрами отрезков наи- меньших длин, соединяющих границы сосуда, и в непрерывном виде она может быть записана как регулярная кривая с натуральной параметризацией. Отсюда од- нозначно можно определить следующие локальные параметры сосудов: направление трассы в каждой точке dx(t) /dt dy(t) / dt

ф ( t ), tg ф ( t ) =

; локальную высоту f (t) , оп- ределяемую расстоянием от текущей точки трассы до её проекции на отрезок L, соединяющий начальную и конечные точки трассы, и кривизну сосудов k(t), k(t) = d2у(t)/dt2. Указанные параметры оцениваются непосредственно по изображению в процессе трасси- ровки и позволяют определить геометрические признаки сосудов, такие как: вариация толщины сосуда (чёт- кообразность) S = rr2 - r2 / r , средняя кривизна

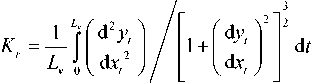
прямолинейность Pr= Lv/L, характеристики конфигураций стенок и трассы. При описании конфигураций стенок и трассы сосуда введём допущение о гармоническом характере функций направления и толщины: r:( t) = ^0cos(to01 + a2),

Для анализа трёхмерной структуры сосудов введём пространственную модель сосудов (рис. 1), описываемую следующим параметрическим уравнением пространственной трассы сосуда:

x = t, y = A1 sin Ю11 sin tort, z = A1 sin to11 cos tort, r = r + A0 sin to01, где A1 – амплитуда колебания трассы, A0 – амплитуда колебания толщины, ω1 – частота колебания трассы, ω0 – частота колебания толщины, ωr – частота враще- ния трассы.

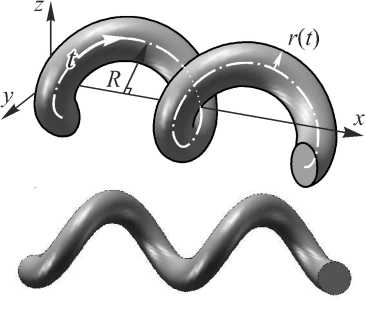
Рис. 1. Пространственная модель сосуда

Как правило, диагностика заболевания осуществляется через визуальную экспертизу ангиограммы и, следовательно , носит субъективный характер, будучи чрезвычайно зависящей от ракурса зарегистрированных проекций. Пространственная модель кровеносной системы служит для визуализации геометрической и топологической информации и позволяет увеличить точность измерений и получить численные оценки геометрических характеристик сосудов [30–35]. В работах [17,22,27] были представлены алгоритмы трассировки сосудов и оценки глобальных признаков сосудов, основанные на предположении о двумерной структуре сосудов. Локальными параметрами, получаемыми в результате трассировки ветви как в двумерном, так и в трёхмерном случае, являются диаметр и направление ветви в каждой точке. Глобальные признаки (средний диаметр, прямолинейность, чёткообразность, амплитуда и частота колебаний толщины, извилистость толщины, амплитуда и частота колебаний трассы, извилистость трассы) вычисляются на основе локальных. В [22,27] приведено определение данных признаков в двумерных структурах и их отличие для трёхмерного варианта. Рассмотрен также специфический признак объёмного изображения, такой как «частота вращения», характеризующий такое пространственное свойство ветви, как отклонение трассы от плоскости.

2.    Методы оценивания признаков

Все рассматриваемые признаки геометрические, они вычисляются с использованием классических определений математического анализа и соответствующих численных методов вычисления расстояний и производных различных порядков. Из-за погрешности исходных данных, связанной с дискретизацией, шумами квантования и геометрическими искажениями, возникающими в устройстве ввода, соответствующие численные методы дают большие погрешности. На примере одного из самых распространённых признаков, описывающих изменяющуюся форму сосуда, – кривизны – можно показать, что относительная погрешность признака неограниченно возрастает в точках перегиба сосуда, причём при уменьшении шага дискретизации количество таких точек увеличивается. Используя численные методы оценивания второй и первой производных и для упрощения делая допущения в равенстве шага дискретизации по вертикали и горизонтали изображения, получим следующее определение кривизны:

K r ( x ) =

У 1 ⁺ У 3 - ² У 2

h ²

,

где  У2 = У(x), У1 = У(x — h), Уз = У(x + h),  дУ = hl2 — максимальная погрешность измерения координаты. Относительная погрешность вычисления признака при аппроксимации производных конечными разностями [36]:

8Kr = E    ln Kr ( У1, У 2, У 3 ) ДУ I = i=1 dyi i=1

K_r h ²

1 + f У^ ) I 2 h )

Табл. 1. Глобальный набор геометрических признаков сосудов

Средний диаметр N D = 2 r = £ r (tn) N n=1 Чёткообразность S = rr2 - r2 / r Прямолинейность N-1 /---------------- Pr = Lv / L = £ 7( xn - xn+1 n-1 2 + ( Уп - Уп+1 )2 (x x1 - xN )2 + ( У1 - yN )2 Амплитуда толщины A = 72 r2 - 2 r2 Частота толщины _    2л    _       . _, . N- , .    ( ,2лnm) ®o = . argmaxR(m), R(m) = £r(tn)exp t N 1< m < N            n=0       I N J Извилистость толщины I0 = A0®0 Амплитуда трассы A1 = 2 f • E (к)j где E(k) – эллип (1+ln (I1+)Л 1171+112 V                     J тический интеграл 2-г N , f = N-1 £| f (tn )|. n-1 о рода Извилистость трассы 11 определяется из уравнения: Pr = (2/л) • 71 +12 • E(к), к = 1771 +12 Частота трассы ®1 = 11/ А1 Частота трёхмерной трассы 1 Ц = — arg max 1m V-1---- _2л/ л      mn £ Rn2 e N =0 , R2n =- 2 A12 cos2®1 tn Частота вращения трассы / 2 к2(1 + A2и,2) ,     -1/'                     2\ иг = и------1——, к = E 1 лPr/ 2^/1 + A2и2 r       1           A12 найденные оценки Pr, A1 и ω1, получаем оценку частоты вращения трассы:

Частота колебаний трассы (для 3D структуры дерева). Для вычисления частоты колебаний трассы ω1 для трёхмерного случая будем использовать преобразование Фурье. Функция R(х) является периодической, но не является синусоидальной, поэтому для повышения точности используем следующий подход: выполняется пре- образование Фурье от центрированной функции R2(x) , где R2(x) = (1/2) • A11(1 - cos2и1x). Тогда получаем оценку частоты трассы:

И

= — arg max 2 ^m

N -1_____ 2л i.

mn

Rn2e N n=0

где R ² _n = - (1 / 2) • Д² cos 2 ц t n .

Частота вращения трассы. Частоту вращения трассы теоретически можно оценить аналогично частоте трассы: и r = (1/2) • argmax S(sin ф( x)), где ф(x) - полярный угол проекции точки трассы на плоскость yOz , но реальные сосуды характеризуются в большинстве случаев малопериодической функцией трассы, что может привести к большой погрешности оценивания признака. Поэтому будем использовать следующий подход. Для кривой (параметрическое уравнение трассы см. выше) значение прямолинейности Pr можно вычислить как Pr = (2 / л) • 7 1+Д2ц2E(к), где к2 = Д2(ц2-иг2)/(1+Д2Ц2), E(•) - полный эллиптический интеграл 2-го рода. Очевидно, что при ωr =0 получаем формулу для плоского случая. Используя иr = ц2 - (к2(1 + Д2Ц2)/Д2), где к2 = E • (пРг / 2^1 + А12и12), где E"*(•) - функция, обратная к эллиптическому интегралу 2-го рода. Таким образом, алгоритм оценки признака состоит из следующих шагов:

• 1)    Определение k, решая численно уравнение относительно k:

E ( к ) = л Pr| 271 + Л.Ч и .                        (1)

• 2)    Вычисление значения оценки по следующей формуле:

и r = 4 ® 1² - ( к ²(1 + AW)/ A 12 ).

У такого подхода есть недостаток. Как известно, максимального значения интеграл второго рода достигает при к = 0: E _max = E (0) = л/2 . Тогда при некотором значении оценки прямолинейности уравнение (1) становится неразрешимым относительно k :

Pr = (2/ л ) • 7 1 + А 12 И 1² E max = V 1 + Д²^² .        (2)

В этом случае переходим на третий шаг алгоритма.

• 3)    Проверка значения оценки прямолинейности. Если оценка превысила значение, вычисляемое по формуле (2), частота вращения трассы оценивается по следующей формуле:

  tor = arg max m

  
  
3.    Экспериментальные исследования оценивания диагностических признаков 3D структуры сосудов

" - 1            - ^{2 П} nm

Z sin ф ( t n ) e "

n = 0

.

Экспериментальные исследования проводились на тестовых трёхмерных изображениях трасс с заданными значениями частот и амплитуд центральных линий и стенок трасс, а также с заданной частотой вращения (рис. 2, 3).

Трасса	ω r			А 1			ω 1
	Ид.	Расч.	^ отн %	Ид.	Расч.	^ отн %	Ид.	Расч.	^ отн %
	0,9	0,879	2,31	1,55	1,527	1,47	1,60	1,599	0,04
	0,95	0,929	2,20	1,52	1,533	0,84	0,82	0,861	5,01
	0,88	0,861	2,13	1,55	1,526	1,55	0,40	0,389	2,75
	1,2	1,230	2,52	0,55	0,523	4,85	0,70	0,718	2,58
	1,1	1,107	0,64	0,5	0,502	0,5	0,35	0,343	1,86
	1,05	1,058	0,76	0,3	0,294	1,83	0,39	0,394	0,95

Рис. 2. Результаты экспериментальных исследований методов оценивания признаков трассы сосудов на тестовых изображениях (ω0 = 9, A0 = 0,1)

Были проведены экспериментальные исследования точности вычисления следующих диагностических признаков сосуда: амплитуды и частоты колебаний трассы, амплитуды и частоты колебаний толщины, частоты вращения. Средняя относительная погрешность вычисления признаков трассы на 100 измерениях составила около 2%, средняя относительная погрешность вычисления признаков толщины составила примерно 1 %. Были проведены также экспериментальные исследования влияния шумов на качество оценок параметров , кластеризация признакового пространства и исследования влияния шумов на количество ошибок кластеризации.

В качестве шумовых воздействий рассматривались аддитивный «белый» гауссовский и импульсный шумы .

Для каждого уровня шума формировалась выборка реализаций, для каждой из которых вычислялся вектор значений относительной погрешности оценок признаков (средней погрешности оценивания признака и пределы доверительного интервала для неё).

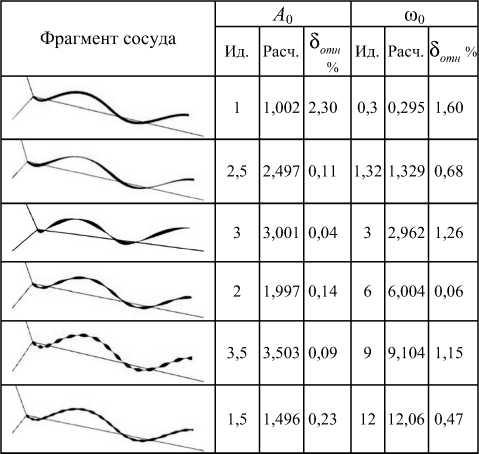
Рис. 3. Результаты экспериментальных исследований методов оценивания признаков стенки сосудов на тестовых изображениях (ω1 = 0,5, ωr = 0,5, А1 = 1)

Степень зашумления определим отношением шум/сигнал: d ² = D_v / D_s , где D_v – дисперсия шума; D_s – дисперсия сигнала. В качестве численного значения дисперсии прин имается евклид ова норма:

D=1IDIL=7 Dx2+Dy2+Dz2.

Исследование влияния аддитивного шума. Рассмотрим статистически независимую выборку, являющуюся последовательностью отсчётов белого шума и имеющую нормальное распределение V1 ,..., v k ~ " (0, о² ). Эта выборка является последовательностью отсчётов белого шума. Прибавив их к исходному многомерному сигналу, получим модель зашумлённого сигнала: f in = x n + v in , i = 1, k , n = 1,4. Для формирования реализаций использовались четыре модели, представленные в табл. 2, выбор которых обусловлен визуальной различимостью пространственных структур.

Табл. 2. Тестовые модели сосудов

Номер модели	Амплитуда трассы	Частота трассы	Частота вращения	Амплитуда колебаний толщины	Частота колебаний толщины	Среднее значение толщины
1	1	0,5	0,5	3	1,32	4
2	2	1	2,14	1	1	4
3	3,1	1,652	2,14	3	1,32	4
4	4	2,54	1,4	3	2	4

Для каждой из моделей генерировалось 25 пространственных структур, использовалось 400 точек трассы с шагом 0,025. Таким образом, для каждого значения шум/сигнал было сформировано 100 реализаций. На рис. 4а представлен график зависимости погрешности оценки амплитуды от величины шум/сигнал. Пунктиром обозначены границы доверительного интервала. Метод оценивания данного признака оказался весьма устойчивым к аддитивным шумовым воздействиям – средняя относительная по- грешность слегка превышает порог в 20 % даже при равной интенсивности сигнала и шума. Верхняя граница доверительного интервала при этом достигает показателя в 24 %. Если задаться некоторым критическим значением погрешности, например в 5 %, то можно сказать, что при значении шум/сигнал, не превышающем 0,13, максимальная погрешность оценки не превзойдёт критического значения с вероятностью 0,95. Средняя погрешность не превысит критического значения при отношении шум/сигнал 0,19.

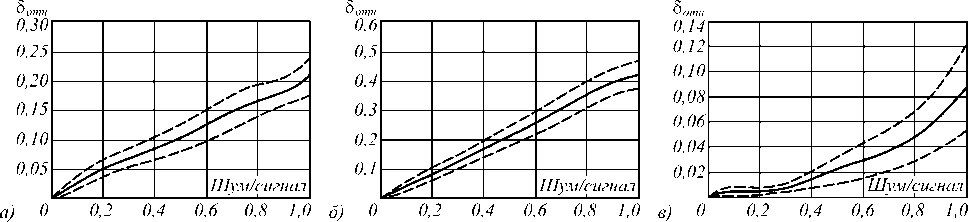
Рис. 4. График зависимости погрешности оценки от уровня шум/сигнал для амплитуды колебаний трассы Aр аддитивный шум (а), импульсный шум (б), после применения фильтра (R = 5) (в)

Исследование влияния импульсного шума. В общем случае модель, описывающая импульсный шум, предполагает, что значения отсчётов сигнала заменяются с некоторой вероятностью случайными или фиксированными значениями. В данных исследованиях использовалась модель шума, когда с заданной вероятностью p = 0,05 происходит сдвиг трёхмерной точки на расстояние R . Причём вектор направленно -сти сдвига является случайным. Исследования проводились для пространственных структур, сформированных на основе описанных в табл. 2 моделей. Для общности анализа (сравнения результатов исследований для разных типов шумов) за отношение шум/сигнал импульсного шума примем следующую величину: ( pD v )/(1- p ) D s . На рис. 4 б приведён график для погрешности оценки амплитуды трассы, анализ которого показал, что импульсный шум имеет более значительное влияние на качество оценки, чем аддитивный. Погрешность в 20 % наблюдается уже при значении отношения шум/сигнал, равном 0,5.

Поэтому для повышения точности оценивания признаков к сигналу применялся медианный фильтр [37].

В ходе экспериментов было выявлено, что наилучшие результаты работы фильтра достигаются при размере окна R, равном 5. На рис. 4в представлены графики зависимости ошибки от уровня шума после применения медианного фильтра. Очевидно, применение фильтра существенно улучшает качество оценивания признаков – величина погрешности не превышает 10 % при соотношении шум/сигнал, равном 1. На рис. 5 для сравнения представлены таблицы относительных погрешностей оценивания признаков для трёх указанных схем исследования (влияние аддитивного шума, импульсного шума и импульсного шума после фильтрации) при сильном зашумлении трассы сосудов (отношение шум/сигнал – 1) и при среднем зашумлении (отношение шум/сигнал – 0,3), представленных выше, в которых градациями серого выделены наилучшие и наихудшие результаты оценивания для различных типов признаков.

Таблицы иллюстрируют степень влияния разного уровня шума различной природы на погрешности оценивания признаков для сравнения в трёх схемах исследования.

Для проверки возможности использования рассмотренных геометрических признаков в качестве диагностических исследовалась возможность отнесения трёхмерной структуры к одному из заранее известных классов.

В качестве алгоритма кластеризации был выбран алгоритм кластеризации на основе метода K- внутригрупповых средних [38]. В качестве признакового пространства выступают векторы оценок признаков.

а:	Схема 1			Схема 2			Схема 3
Ошибка	Макс.	Ср.	Мин.	Макс.	Ср.	Мин.	Макс.	Ср.	Мин.
Амплитуда трассы	0,242	0,213	0,185	0,477	0,431	0,385	0,12	0,08	0,06
Частота трассы	0,056	0,031	0,014	5,028	2,476	0,001	0,822	0,261	0,001
Частота вращения	0,058	0,046	0,012	0,1924	0,1535	0,1147	0,1166	0,0833	0,05
Прямолинейность	0,252	0,171	0,121	3,355	3,422	3,313	0,776	0,484	0,337
Извилистость трасс	0,301	0,254	0,211	4,833	2,963	0,515	0,362	0,187	0,001
Средний диаметр	0,037	0,025	0,01	0,037	0,023	0,016	0,021	0,015	0,004
Четкообразность	0,146	0,091	0,035	0,452	0,378	0,305	0,122	0,097	0,054
Амплитуда толщ.	0,132	0,088	0,044	0,436	0,384	0,333	0,137	0,091	0,045
Частота толщины	0,0230	0,0115	0,001	0,0646	0,0323	0,001	0,0034	0,0017	0,001
Извилистость толщ.	0,132	0,093	0,044	0,436	0,384	0,333	0,126	0,082	0,046

б:	Схема 1			Схема 2			Схема 3
Ошибка	Макс.	Ср.	Мин.	Макс.	Ср.	Мин.	Макс.	Ср.	Мин.
Амплитуда трассы	0,0803	0,0685	0,0567	0,1501	0,1265	0,1030	0,0091	0,0066	0,0041
Частота трассы	0,0375	0,0188	0,0001	1,001	0,5005	0,0001	0,0001	0,0003	0,0001
Частота вращения	0,0358	0,0185	0,0012	0,1024	0,0645	0,0267	0,0104	0,0052	0,0002
Прямолинейность	0,0674	0,05	0,0174	1,4988	1,2494	1,0001	0,051	0,0255	0,0001
Извилистость трасс	0,1032	0,0851	0,067	1,6734	0,8367	0,0001	0,0002	0,0001	0,0003
Средний диаметр	0,0146	0,0095	0,0044	0,015	0,01	0,005	0,0028	0,0017	0,0006
Четкообразность	0,0536	0,0363	0,019	0,1343	0,1121	0,0898	0,0167	0,0083	0,0001
Амплитуда толщ.	0,0506	0,0337	0,0168	0,1424	0,1118	0,0812	0,0071	0,0036	0,0003
Частота толщины	0,0034	0,0017	0,0001	0,032	0,016	0,0001	0,0024	0,0012	0,0002
Извилистость толщ.	0,0506	0,0337	0,0168	0,149	0,117	0,0853	0,0167	0,0083	0,0001

Рис. 5. Таблицы относительных погрешностей оценивания признаков для отношения шум/сигнал: 1 (а), 0,3 (б) (схема 1 - аддитивный шум, схема 2 - импульсный шум, схема 3 - после применения фильтра (R=5))

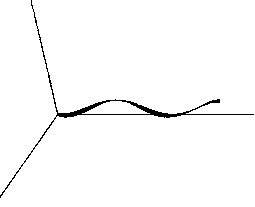
В данных исследованиях выборка для кластеризации создавалась на основе нескольких заданных моделей (рис. 7), которые и являлись начальными центрами кластеров. В табл. 3 представлены значения оценок признаков для реализаций, сформированных на основе этих моделей. Выбор таких моделей обусловлен визуальной различимостью пространственных структур, моделируемых на их основе. На рис. 7 представлены сформированные реализации для исходных моделей (1 – 3 модели). Для кластеризации были сгенерированы 150 тестовых реализаций путём случайных изменений параметров исходных моделей.

В результате эксперимента из 150 сгенерированных тестовых изображений сосудов правильно кластеризованные – 137, для 13 (2 – для 1-й модели, 4 – для 2-й модели, 7 – для 3-й модели) алгоритм класте- ризации дал неверный результат с точки зрения того, на основе какой модели был сформирован сосуд. Таким образом, была показана диагностическая значимость признаков.

Табл. 3. Модели начальных центров кластеров

Признак	Модель 1	Модель 2	Модель 3
Амплитуда трассы	1,02	3,93	2,77
Частота трассы	0,53	1,54	1,41
Частота вращения	0,52	2,62	1,67
Прямолинейность	1,2	8,1	4,31
Извилистость трассы	0,58	6,05	3,83
Средний диаметр	8,47	8,41	8,47
Чёткообразность	0,49	0,5	0,48
Амплитуда толщ.	2,9	2,96	2,88
Частота толщины	1,34	2,12	1,44
Извилистость толщ.	3,89	6,31	4,15

а)

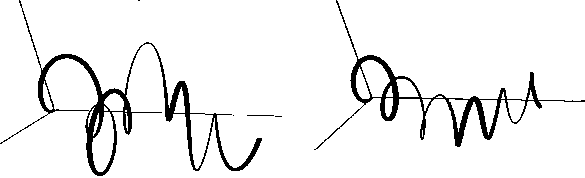
б)                                        в)

Рис. 6. Вид смоделированных структур для исходных моделей: модель 1 (A = 1; ю = 0,5; to r = 0,5; A₀ = 3; to ₀ = 1,32) (a); модель 2 (A = 4; to = 1,4; to , = 2,54; A₀ = 3; to ₀ = 2) (б); модель 3 (A = 2,5; to = 1,5; to , = 1,5; A₀ = 3; to o = 1,4) (в)

Заключение

Предложена новая обобщённая математическая модель изображений сосудов глазного дна и коронарных сосудов сердца, позволяющая формализовать описание геометрических параметров, оценить их и осуществить формирование диагностических признаков. Определён базовый набор геометрических параметров сосудов, включающий распределение локальных оценок направлений и толщины сосудов, который лёг в основу методологии выделения диагностически значимой информации на изображениях кровеносных сосудов. Представлены методы и алгоритмы для оценки геометрических параметров 3D сосудистых структур. Экспериментальные исследования влияния аддитивного и импульсного шумов на качество оценок диаг- ностических признаков, кластеризация признакового пространства на модельных изображениях, а также исследования влияния шумов на количество ошибок кластеризации подтвердили устойчивость работы предложенных методов оценивания глобального набора 3D признаков сосудов. При этом средняя погрешность оценки признаков не превышает 5 % при значении шум/сигнал, не превышающем 0,20.

Эксперименты показали, что импульсный шум имеет наибольшее влияние на качество оценки признаков. Для повышения точности оценивания признаков необходимо применять медианный фильтр с размером окна, равным 5. Кластерный анализ продемонстрировал принципиальную возможность использования признаков в качестве диагностических характеристик состояния со- судов. Ошибка классификации на трёх моделях, выбор которых обусловлен визуальной различимостью пространственных структур, составила 8 %.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научнообразовательных центров на 2013–2020 годы; грантов РФФИ 12-01-00237-а, 14-01-00369-а, 14-07-97040-р_поволжье_а; программы № 6 фундаментальных исследований ОНИТ РАН «Биоинформатика, современные информационные технологии и математические методы в медицине» 2013–2014 гг.