Оценивание неопределённости в машинном обучении
Автор: Арьков В.Ю., Шарипова А.М., Куликов Г.Г.
Рубрика: Информатика и вычислительная техника
Статья в выпуске: 3 т.23, 2023 года.
Бесплатный доступ
Большинство методов машинного обучения основаны на статистической теории обучения, при этом часто используется упрощение процедур для достижения приемлемой скорости вычислений. Цель исследования. Сформировать общий подход к оценке неопределенности в моделях машинного обучения. В эконометрике в любой модели в обязательном порядке ставится неопределенность в форме стандартного отклонения («сигмы») для коэффициентов и для прогнозов. Проблема заключается в том, что в машинном обучении нельзя аналитически посчитать неопределенность через «сигму». Поэтому вместо аналитических методов мы предлагаем использовать численные методы. Материалы и методы. Для детального рассмотрения вопроса оценивания неопределённости выбраны классические методы регрессионного анализа, в которых уделяется большое внимание неопределённости коэффициентов модели и - что более важно - точности прогнозов, полученных по такой модели. Результаты. Предлагается технология оценки неопределённости, демонстрируемая на модельном примере для того, чтобы показать, что она согласуется с традиционными классическими методами по результатам. В дальнейшей практике мы предлагаем использовать кросс-валидацию. Заключение. При использовании машинных моделей сложных процессов, в том числе прогнозов, построенных по таким моделям, при принятии управленческих решений становится всё более актуальной проблема оценивания неопределённости и вытекающих из этой неизбежной неопределённости рисков. Данная проблема может быть решена на основе непараметрических методов, хотя для этого потребуется гораздо большая вычислительная мощность, чем та, которая используется для обучения машинной модели. Предлагаемый подход можно обобщить и для других методов машинного обучения, например, для задачи классификации и кластеризации.
Неопределённость параметров, обучение с учителем, моделирование, методы прогнозирования
Короткий адрес: https://sciup.org/147241768
IDR: 147241768 | УДК: 004.8 | DOI: 10.14529/ctcr230305
Текст научной статьи Оценивание неопределённости в машинном обучении
За последние десятилетия в различных областях деятельности быстро распространяются технологии машинного обучения. Это происходит по различным причинам, включая растущий объём данных, доступных в цифровой форме, достаточную вычислительную мощность даже на уровне настольных персональных компьютеров, а также благодаря большому количеству свободно распространяемого программного инструментария, например библиотеки Sci-Kit Learn для языка Python.
Машинное обучение часто рассматривается как извлечение полезной информации и даже знаний из «сырых» необработанных данных – область деятельности, частично пересекающаяся по решаемым задачам и используемым методам с искусственным интеллектом. Существующие алгоритмы машинного обучения позволяют подстраивать структуру и параметры модели по имеющимся экспериментальным данным, которые в данном случае называют «обучающей выборкой». В процессе обучения модели производится оптимизация выбранного (обычно квадратичного) критерия качества. Далее производится подтверждение качества модели, которое также называется термином «валидация». Для этого используется контрольная выборка – часть исходной выборки, которая не участвовала в обучении модели. Такая валидация проводится многократно путём различного разделения исходной выборки на обучающую и контрольную, в результате чего часто используется термин «кросс-валидация», или «скользящая проверка». За счёт кросс-валидации пытаются обеспечить обобщающие свойства машинной модели и исключить «переобучение», то есть подгонку модели под конкретную выборку.
Зачастую обнаруживается, что многие технологии машинного обучения реализуют уже известные и хорошо проработанные статистические методы, такие как, например, метод наименьших квадратов (МНК). Отметим, что традиционный, классический МНК позволяет получить не только параметры регрессионной модели, но и оценить их неопределённость в форме некоторых параметров распределения оценок коэффициентов полученной модели. Чаще всего распределение характеризуется двумя параметрами – математическим ожиданием и стандартным отклонением. В данном случае используется аналитический подход к оценке неопределённости – в предположении, что для описания гауссовского распределения будет достаточно использовать два параметра, а в МНК используется именно это предположение о нормальности случайной составляющей. Следующим шагом является построение доверительных интервалов при заданной вероятности – вначале для коэффициентов модели, а затем и для прогнозов.
К сожалению, многие существующие инструменты нацелены на обучение модели и её валидацию, при этом гораздо меньше внимания уделяется изучению статистических свойств полученных оценок. Кроме того, проблема кросс-валидации не так основательно исследована, как процесс обучения модели, что, скорее всего, объясняется ограничениями в плане доступной вычислительной мощности. Данное предположение частично подтверждается тем фактом, что, не- смотря на все общеизвестные ограничения и недостатки, в машинном обучении широко используется квадратичный критерий качества. Отметим, что первоначально метод наименьших квадратов использовался в ручных расчётах. Тем не менее, сумма квадратов отклонений по-прежнему используется как основной критерий качества, в том числе для алгоритмов глубокого обучения, реализуемых на мощных суперкомпьютерах.
В данной работе предлагается находить оценку неопределённости моделей машинного обучения на основе технологий кросс-валидации. Предлагаемый подход до некоторой степени аналогичен оценке неопределённости в метрологии через имитационное моделирование, хотя и основан на аналитическом подходе, используемом в статистических процедурах.
1. Квадратичные критерии машинного обучения
Выясняется, что процесс кросс-валидации является очень требовательным к вычислительным ресурсам. Более того, тщательное проведение кросс-валидации может потребовать гораздо больше вычислений, чем собственно обучение машинной модели [1]. В результате пользователю зачастую предлагается провести лишь небольшое количество разбиений исходной выборки на обучающую и контрольную. Например, в работе [2] Лакшминарайанан описывает эксперименты с обучением ансамблей глубоких нейросетей с попыткой оценивания неопределённости. Здесь многослойные нейросети обучаются на «стандартном» наборе данных по бостонским объектам недвижимости. Автор упоминает в качестве максимального количества двадцать разделений исходного набора данных на обучающую и контрольную выборки. После обучения производилось оценивание качества моделей регрессии и классификации. Хотя в данном примере для каждой метрики качества были получены оценки неопределённости в виде интервалов значений, сам объём работы по кросс-валидации скорее всего нельзя считать достаточным.
Чтобы подчеркнуть важность оценивания неопределённости, следует напомнить так называемые «четыре типа аналитики». Первое – это описательная аналитика, раздел статистики, описывающий форму и параметры распределения случайной величины. Здесь выполняется описание событий прошлого в форме различных обобщающих показателей типа минимума, максимума, среднего и стандартного отклонения. Далее следует второй тип – диагностическая аналитика, указывающая предполагаемые причины событий прошлого.
Третий тип аналитики – предиктивная (предсказательная); это инструмент для построения прогнозов и предсказаний. Такое применение машинных моделей явным образом реализовано в статистическом обучении, например, в форме прогнозирования по регрессионным моделям. Джеймс и Хэйсти в работе [3] подчёркивают, что включение в модель слишком большого количества объясняющих переменных, не связанных напрямую с изучаемым объектом, не обязательно улучшают прогностические возможности машинных моделей, таких как регрессия.
Прогностические модели могут также содержать оценивание неопределённости, указывает Саксена [4]. В указанной работе для неопределённости прогнозов строится непараметрическое описание в предположении негауссовского распределения, которое в дальнейшем аппроксимируют аналитической функцией.
Четвёртый тип – предписывающая аналитика – выдаёт рекомендации по принятию решений на основе машинных прогнозов, см., например, работу Фатера и Нолла [5]. Этот этап ближе к управлению предприятием и производственными процессами, чем к анализу данных как таковому. Отметим, что принятие решений должно включать оценку рисков и управление рисками, что требует оценивать неопределённость использованных прогнозов.
Метод наименьших квадратов используется при построении математических моделей как технических, так и экономических систем, см. работу Ванга [6]. Математическое моделирование технических объектов по реальным данным часто относят к технологиям идентификации моделей, в то время как построение математических моделей экономических систем проводится в рамках технологий эконометрики (эконометрии). Несмотря на некоторое различие в терминологии, технологии идентификации и эконометрики во многом схожи.
Регрессионный анализ в области идентификации систем и эконометрики позволяет получать модели в форме уравнения с коэффициентами и их стандартными отклонениями, как бу- дет показано ниже. Далее следует построение доверительных интервалов (пределов значений оценок) и проверка статистической значимости полученных оценок коэффициентов. В этом случае моделирование проводится в предположении нормальности распределения результатов регрессионного анализа, что является следствием вычислений по методу наименьших квадратов.
Следует подчеркнуть, что, в отличие от экономических систем, однотипные технические объекты часто производятся в большом количестве в рамках серийного производства. При этом конструкция и характеристики современной техники подчиняются требованиям стандартов, а также конструкторской и технологической документации. Такими образом, в технических науках открываются возможности для построения усреднённых математических моделей, которые затем можно индивидуально уточнять по экспериментальным данным, как описано в работе Аль-Саида [7].
Интеллектуальный анализ данных – data mining – представляет собой подход к поиску скрытых закономерностей и взаимосвязей в больших массивах данных, как описано в работе Лесковец [8]. Первоначально эта методология называлась «разведочный анализ данных», см. работы Тьюки [9] или Брюса [10]. Техники разведочного и интеллектуального анализа данных также включают в себя регрессию и МНК.
2. Неопределенность моделей
Математические модели, полученные методами машинного обучения, представляют собой более сложные объекты, чем традиционные результаты МНК. Количество параметров машинных моделей с каждым годом возрастает по мере увеличения доступных вычислительных ресурсов. Например, предварительно обученная модель GPT-3, построенная по технологии глубокого обучения, использует сотни миллиардов параметров для обработки естественного языка. Такой уровень сложности полностью исключает любые попытки аналитически оценить неопределённость каждого коэффициента модели. При описании подобных моделей большое внимание уделяется успешным примерам применения, в то время как оценки неопределённости оставляют без внимания, см., например, статью Корнгибеля и Мууни [11] с обсуждением возможностей машинной замены живого общения.
С другой стороны, методика кросс-валидации предоставляет дополнительные инструменты для численного (непараметрического) оценивания неопределённости, хотя при этом требуется гораздо больше вычислительных ресурсов, чем для собственно обучения машинной модели.
Метод наименьших квадратов в регрессионном анализе достаточно подробно проработан и исследован, см. работу Снедекора [12]. Здесь обычно предполагается постоянная дисперсия случайной составляющей (ошибки, остатков), что в эконометрике называют термином «гомоскеда-стичность».
Подробно обсуждение основ МНК можно найти в многочисленной литературе по эконометрике, такой как работа Фомби, Джонсона и Хилла [13]. Для успешного применения МНК требуется выполнение ряда необходимых предпосылок, описанных в теореме Гаусса – Маркова; за этим следует обсуждение свойств сходимости, состоятельности и т. п. Теорема Гаусса – Маркова отражает обобщённый подход к регрессионному анализу, см. работы Конга [14], Лайке [15], Дру-гаса [16] или Циммермана [17].
В идеале оценки коэффициентов уравнения регрессии должны сопровождаться оценками их стандартных отклонений, как показано в примере ниже.
a + b х.
(^ a ) (P b )
У
Типичная последовательность действий в регрессионном анализе включает следующие шаги: 1) оценка уравнения регрессии;
-
2) построение точечного и интервального прогноза;
-
3) построение графиков линии регрессии и доверительного интервала для результативного признака;
-
4) оценка остатков и анализ свойств и графиков остатков.
Завершающая стадия представляет собой проверку выполнения предпосылок МНК – условий, описанных в теореме Гаусса – Маркова, что обеспечивает желательные асимптотические свойства оценок, таких как нормальность, эффективность и состоятельность.
Далее рассмотрим вычислительный эксперимент, описанный Грином в [18]. Имитационное моделирование по методу Монте-Карло позволяет получить непараметрическое представление распределения оценок по МНК. Модифицируем план эксперимента для удобства демонстрации следующим образом. Факторный признак x генерируется как равномерно распределённая случайная величина. Результативный признак y линейно коррелирован с фактором x . Прибавляем нормально распределённое случайное возмущение e , как показано ниже.
y = x – 100 + e ;
x ~ U (150; 200); (2)
e ~ N (0; 10).
Данная обучающая выборка генерируется 1000 раз с объёмом каждой выборки 100 наблюдений.
По каждой обучающей выборке проводится построение уравнения регрессии и оценка коэффициентов уравнения. Для дальнейшего рассмотрения будем изучать поведение оценки коэффициента регрессии, определяющего наклон линии регрессии. Используя полученную «выборку» оценок коэффициента, проводят оценку формы распределения в виде гистограммы и диаграммы размаха (box-and-whiskers plot) (рис. 1). Поскольку распределение оценок по МНК должно быть близко к нормальному, для сравнения построена гауссовская кривая плотности вероятности для соответствующих среднего значения и стандартного отклонения.
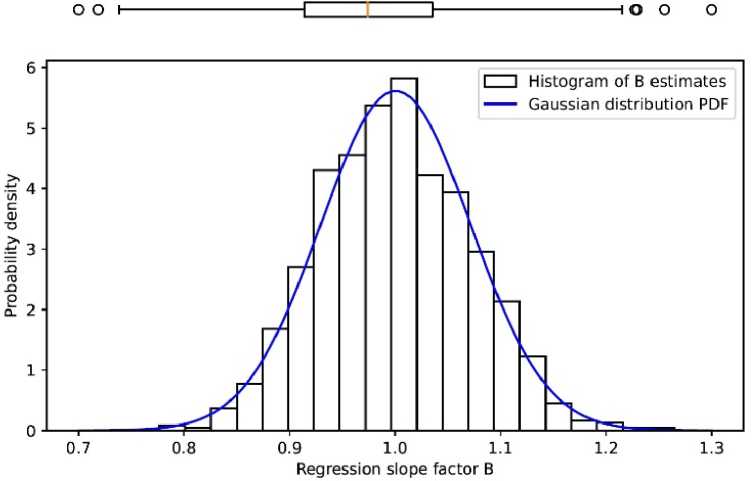
Рис. 1. Распределение оценок коэффициента регрессии Fig. 1. Distribution of regression coefficient estimates
Рассмотрим расширенное представление результатов имитационного моделирования. На рис. 2 изображён ряд линейных прогнозов, причём на заднем фоне приводятся все выборки (наборы исходных данных). Можно видеть, что дисперсия прогноза возрастает, когда значение факторного признака х приближается к границам диапазона известных значений. Поскольку мы сгенерировали 1000 выборок и по каждой из них провели оценивание линейной модели, общая продолжительность вычислительного эксперимента в 1000 раз больше, чем однократное получение оценки по МНК.
После проведения дисперсионного анализа неопределённости оценок (ANOVA) строятся доверительные интервалы на основе оценок стандартного отклонения прогноза [19]. Таким образом, неопределённость прогнозов оценивают «почти аналитически», что невозможно реализовать для сложных моделей машинного обучения.
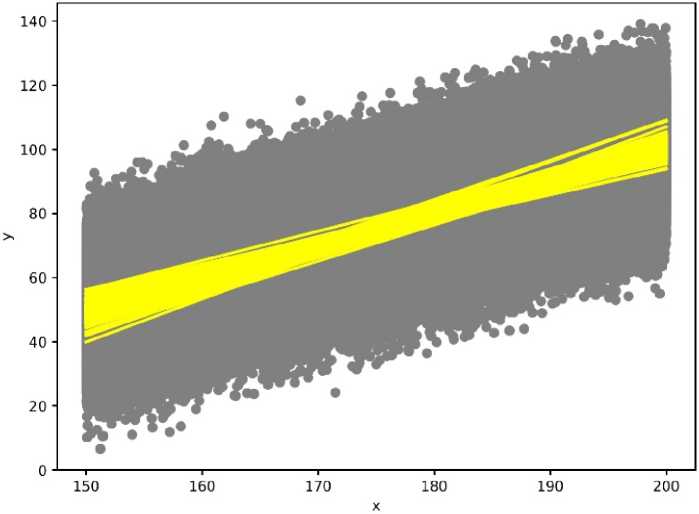
Рис. 2. Линейные прогнозы для серии выборок Fig. 2. Linear predictions for a series of samples
Экстраполируя описанную логику аналитического оценивания неопределённости в машинном обучении, можно было бы ожидать подобные оценки в виде стандартного отклонения для каждого параметра, как показано на рис. 3. Каждая оценка значения параметра сопровождается его стандартным отклонением, что должно приводить к оцениванию дисперсии прогнозов.
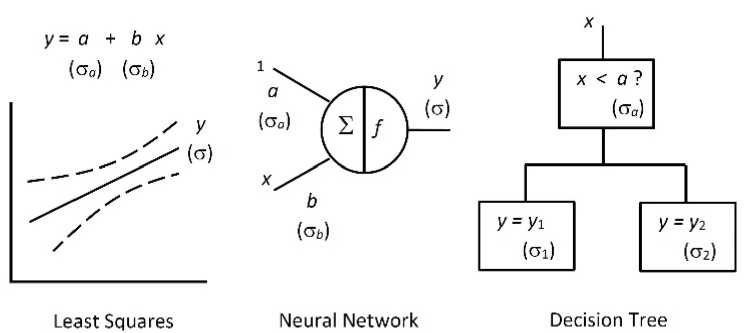
Рис. 3. Аналитическое представление неопределённости в машинном обучении Fig. 3. Analytical representation of uncertainty in machine learning
Однако в большинстве случаев аналитический подход к изучению машинных моделей практически неприменим по ряду причин – и прежде всего из-за очень высокой сложности и нелинейности модели. Именно поэтому применение МНК для нелинейных систем сводится к «линеаризации» моделей за счёт включения в линейное уравнение нелинейных членов, которые рассматриваются как дополнительные «линейные регрессоры».
Рассмотрение истории вопроса и сравнительный анализ приводит к выводу о том, что методы машинного обучения предлагают гораздо менее ясное представление полученных моделей и меньший уровень понимания их внутреннего устройства. Возможное объяснение для отсутствия этапа серьёзного анализа результатов моделирования заключается в том, что машинная модель и алгоритмы машинного обучения строятся полностью на основе обучающей выборки и не учитывают априорное или экспертное знание об изучаемом объекте [20].
3. Постановка задачи
Задачи оценивания неопределённости формулируются следующим образом. В нашем распоряжении имеется набор исходных экспериментальных данных (обучающая выборка), содержащая линейно коррелированные факторный и результативный признаки. Требуется оценить неопределённость прогнозов значений результативного признака в виде доверительного интервала, предпочтительно малочувствительного к выбросам (аномалиям). Чтобы продемонстрировать предлагаемый подход, используется упрощённая постановка задачи, которую можно затем обобщить на задачу нелинейного многомерного моделирования.
Рассмотрим постановку задачи более подробно. Исходные данные для машинного обучения подготовлены для анализа и представлены в табличной форме, где факторный и результативный признаки расположены по столбцам как ( x , y ). Считаем, что результативный признак y линейно связан с фактором x . Коэффициенты линейного уравнения считаем неизвестными. Данные содержат аддитивный случайный шум с нормальным распределением.
На основе предложенного набора данных обучается некоторая машинная модель M(c) , содержащая большое количество параметров (коэффициентов) c . Обучение машинной модели производится так, чтобы минимизировать квадратичный критерий отклонения фактического и прогнозного значений результативного признака: ∑∆ y 2 → min. В процессе обучения машинной модели определяются её структура и параметры так, чтобы обеспечить обобщённое описание взаимосвязи вход-выход за счёт разделения данных на обучающую и контрольную выборки в заданном соотношении.
Задаём значения факторного признака в пределах интервала известных значений обучающей выборки X и получаем прогноз значений результативного признака Y с помощью обученной модели, содержащей оценки параметров c .
Наконец, требуется оценить неопределённость прогноза выхода модели как интервал возможных значений, соответствующий доверительному интервалу и менее чувствительному к выбросам, а также к «толстым хвостам» распределения Y . В целях наглядности представления будем рассматривать два типа машинных моделей – линейную регрессию и случайный лес.
4. Вычислительный эксперимент
Рассмотрим постановку вычислительного эксперимента в среде Python для исследования неопределённости оценок и прогнозов. Предлагаемый нами непараметрический подход к оцениванию неопределённости прогнозов по регрессионной модели имеет некоторое сходство с экспериментами Грина по методу Монте-Карло [18]. Отметим, что регрессионный анализ представляет собой пример численных методов и непараметрического подхода к анализу данных [19]. Общая идея оценивания через моделирование распространяется на изучение свойств прогнозов следующим образом.
Будем многократно (в цикле) генерировать обучающую выборку – каждый раз с новым состоянием генератора случайных чисел, что обеспечивается автоматически при новом вызове функций RAND и RANDN. Далее обучаем машинные модели по новой выборке. Обе выбранные модели – линейная регрессия и случайный лес – используют квадратичный критерий в процессе обучения и поэтому обеспечивают сходные результаты в плане прогнозирования. Значения факторного признака для построения прогноза линейно нарастают на протяжении выбранного интервала за счёт использования функции LINSPACE и соответствуют диапазону значений фактора в обучающей выборке. При многократном повторении этапов генерирования данных и обучения модели на каждой итерации цикла строим прогнозы для одних и тех же значений фактора по каждой вновь полученной модели. Затем собираем все прогнозные значения в массив для дальнейшей обработки и оценивания распределения.
Общая форма распределения прогнозов представлена на рис. 4 в виде гистограмм. Рассматриваются два крайних значения фактора и соответствующие им прогнозы для результативного признака: y (150) и y (200). В то время как прогнозы по МНК имеют нормальное распределение, прогнозы модели типа случайный лес дают несколько иные результаты. Чтобы исследовать указанные различия, на график также нанесены гауссовские кривые плотности вероятности, построенные с фактическими значениями среднего и сигмы, вычисленными для массива прогнозов.
Sampling distribution of predictions
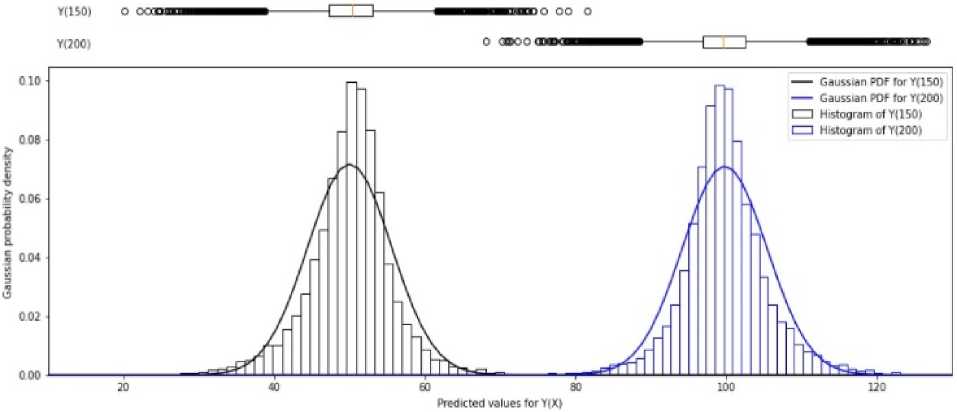
Рис. 4. Диаграммы размаха и гистограммы для прогнозов по случайному лесу Fig. 4. Box plots and histograms for random forest forecasts
На рис. 4 также приведены диаграммы размаха по обоим прогнозным значениям. Как можно видеть, оба распределения обладают островершинностью (эксцессом) и имеют достаточно длинные «хвосты», что подтверждается большим количество выбросов за пределами квартильного интервала. Центральная часть кривых более узкая – по сравнению с теоретическим гауссовским распределением. На рис. 5 показано общее расположение всех обучающих выборок (серые маркеры), а также прогнозы, полученные по регрессионной модели. Центральная кривая, соответствующая линии регрессии, получена как медиана всех прогнозов для заданного значения фактора. Нижняя и верхняя границы диапазона прогнозных значений рассчитываются исходя их квартильной вариации как отклонения от медианы на полтора межквартильных размаха – в соответствии с методикой построения диаграммы размаха.
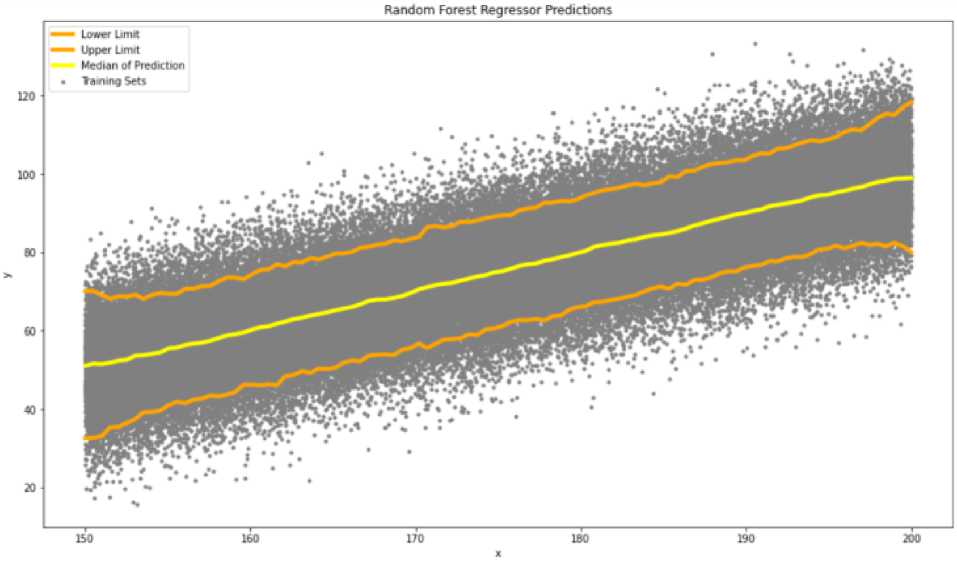
Рис. 5. Неопределённость прогнозов по случайному лесу в форме квартильной вариации Fig. 5. Uncertainty of the random forest predictions in the form of quartile variation
Три квартиля Q1, Q2 и Q3 получены по массиву (выборке) прогнозов с использованием интерполяции для чётного объёма выборки. Межквартильный размах IQR определяется как расстояние между первым и третьим квартилями. Оценки нижней и верхней границы диапазона прогнозных значений находятся так, чтобы получить оценки, близкие к доверительным интервалам «три сигмы» при уровне доверительной вероятности около 99,7 %.
Основные соотношения для расчётов выглядят следующим образом:
IRQ = Q3 – Q1
Median = Q2
Low limit = Q1 – 1.5 IQR
Upper limit = Q3 + 1.5 IQR
В дополнение к оцениванию неопределённости прогнозов можно констатировать сглаживающий эффект за счёт квантильного усреднения регрессионных оценок. Как медиана, так и границы интервалов для прогноза становятся более гладкими – по сравнению с индивидуальным прогнозом, полученным по одной выборке (см. рис. 5). На рис. 5 и 6 построенные по модели прогнозы демонстрируют общие свойства оценок МНК: наклон линии регрессии несколько ниже, чем наклон исходной линии. Таким образом, оценка коэффициента регрессии оказывается меньше, чем соответствующий параметр исходной модели, по которой были сгенерированы данные. Следует отметить, что аналогичное поведение характерно для многих моделей машинного обучения, когда используется квадратичный критерий качества, а после обучения модели определяют квадратичную метрику качества.
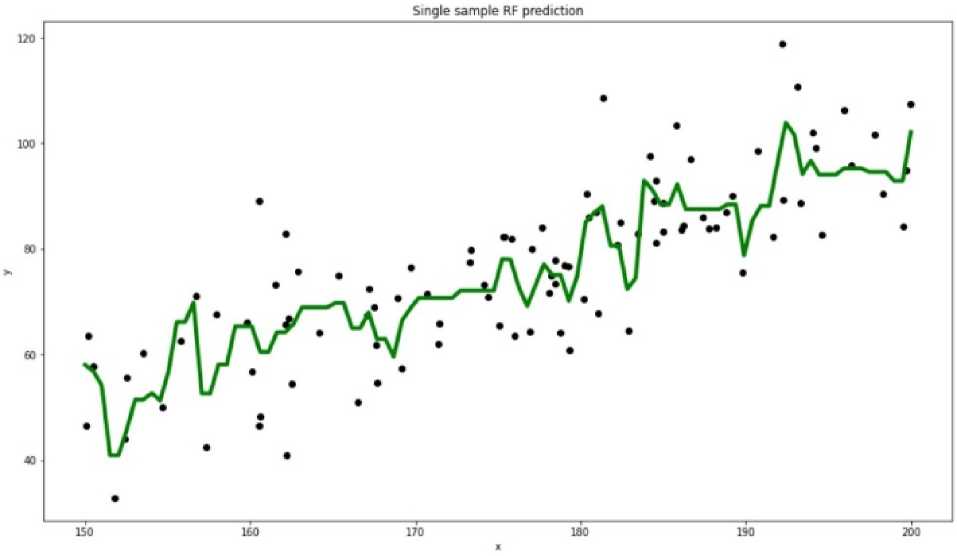
Рис. 6. Прогноз результативного признака для случайного леса, обученного по одной выборке Fig. 6. Predicted output of random forest trained on single sample
Недавние усовершенствования в области интерактивных параллельных вычислений предоставляют дополнительные возможности для приложений машинного обучения на основе Python, R или MATLAB [21, 22]. Кроме того, недавно стал доступен автоматический инструментарий машинного обучения AutoML, что облегчает работу большого числа исследователей данных. Распространённый пример AutoML – пакет Auto-sklearn [23], в котором особое внимание уделяется оптимизации гиперпараметров. Отметим, что на каждой итерации обучения Auto-sklearn создаёт целый ансамбль моделей. Далее выполняется упрощённая оценка ошибки в форме медианного значения, а также 5-го и 95-го процентилей, что является побочным результатом оценивания и может выступать в качестве меры неопределённости.
Выводы и дальнейшая работа
В данной работе рассмотрен общий подход к проведению регрессионного анализа, а результаты экстраполированы на оценивание неопределённости в моделях машинного обучения, чтобы заполнить нишу в существующих программных пакетах. Предлагаемый непараметрический подход основан на технике кросс-валидации и позволяет получать оценки неопределённости для прогнозов, полученных на основе машинных моделей. В то время как аналитическое оценивание неопределённости затруднено в связи с существенной нелинейностью машинных моделей, непараметрический подход позволяет получить альтернативные оценки для прогнозных значений. Следует отметить, что стандартное отклонение как мера неопределённости может адекватно описывать гауссовское распределение, которое не всегда присутствует в реальных данных. Поэтому предлагается в качестве стандартной меры разброса использовать «квартильную вариацию» на основе диаграммы размаха, что является более гибким, универсальным и статистически устойчивым средством.
Дальнейшие исследования в области оценивания неопределённости машинных прогнозов могут распространить предложенный подход на другие методы машинного обучения, такие как классификация, кластеризация и снижение размерности. При работе с большими массивами реальных данных исследователю придётся использовать вычислительные ресурсы суперкомпьютера, поскольку оценивание неопределённости через многократную кросс-валидацию требует вычислительной мощности – гораздо большей, чем для обучения машинной модели. Приемлемый уровень ускорения вычислений может быть достигнут, например, при использовании графических процессоров.
Список литературы Оценивание неопределённости в машинном обучении
- Arkov V.U. Uncertainty estimation in mechanical and electrical engineering. In: International Conference on Electrotechnical Complexes and Systems ICOECS. Manchester, U.K. 2021. P. 436-440.
- Lakshminarayanan B., Pritzel A., Blundell C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In: 31st Conference on Neural Information Processing Systems NIPS. Curran Associates Inc., Red Hook, NY, USA. 2017. P. 6405-6416.
- James G., Witten D., Hastie T., Tibshirani R. An Introduction to Statistical Learning. Springer, NY; 2021. 426 p.
- Saxena A., Celaya J., Saha B., Saha S., Goebel K. Evaluating prognostics performance for algorithms incorporating uncertainty estimates. In: IEEE Aerospace Conference Proceedings. 2010. P. 1-11. DOI: 10.1109/AER0.2010.5446828
- Vater J., Harscheidt L., Knoll A. Smart Manufacturing with Prescriptive Analytics. In: Proceedings of the 8th International Conference on Industrial Technology and Management ICITM. 2019. P.224-228.
- Wang L., Garnier H. System Identification, Environmental Modelling, and Control System Design. Springer, London; 2012. 648 p.
- El-Sayed A.F. Aircraft Propulsion and Gas Turbine Engines. CRC Press, Boca Raton; 2017. 1476 p.
- Leskovec J., Rajaraman A., Ullman J. Mining of Massive Datasets. Cambridge: Cambridge University Press; 2020. 565 p.
- Tukey J.W. Exploratory data analysis. Addison-Wesley; 1977. 712 p.
- Bruce P., Bruce A. Practical Statistics for Data Scientists. O'Reilly Media; 2017. 368 p.
- Korngiebel D., Mooney S. Considering the possibilities and pitfalls of Generative Pre-trained Transformer (GPT-3) in healthcare delivery. Digital Medicine. 2021;4(1):93. DOI: 10.1038/s41746-021-00464-x
- Snedecor G.W. Statistical methods. Iowa State University Press; 1938. 356 p.
- Fomby T.B., Johnson S.R., Hill R.C. Review of Ordinary Least Squares and Generalized Least Squares. In: Advanced Econometric Methods. Springer, New York, NY; 1984. DOI: 10.1007/978-1-4419-8746-4_2
- Kong Q., Siauw T., Bayen A. Least Squares Regression. In: Python Programming and Numerical Methods: A Guide for Engineers and Scientists. Academic Press. 2021. P. 279-293.
- Lyche T. Least Squares. In: Numerical Linear Algebra and Matrix Factorizations. Texts in Computational Science and Engineering book series 22. Springer International Publishing. 2020. P. 199-222.
- Drygas H. Consistency of the least squares and Gauss-Markov estimators in regression models. Z. Wahrscheinlichkeitstheorie verw Gebiete. 1971;17:309-326.
- Zimmerman D.L. Least Squares Estimation for the Gauss-Markov Model. In: Linear Model Theory. Springer, Cham. 2020.
- Greene W. Econometric Analysis. Pearson, New York; 2020.
- Kiusalaas J. Numerical Methods in Engineering with Python 3. Cambridge University Press, Cambridge; 2013.
- Sohil F., Sohail M., Shabbir J. An introduction to statistical learning with applications in R. Springer Science and Business Media. New York; 2013.
- Reuther A. et al. Interactive Supercomputing on 40,000 Cores for Machine Learning and Data Analysis. In: 2018 IEEE High Performance extreme Computing Conference (HPEC). 2018. P. 1-6. DOI: 10.1109/HPEC.2018.8547629
- Raschka S., Patterson J., Nolet C. Machine Learning in Python: Main developments and technology trends in data science, machine learning, and artificial intelligence. 2020. arXiv:2002.04803v2. DOI: 10.48550/arXiv.2002.04803
- Feurer M. et al. Auto-sklearn: Efficient and Robust Automated Machine Learning. In: Automated Machine Learning. 2019.


