Оценивание параметров положения контура кривой в профильной системе

В профильных системах неразрушимого контроля широко используются профильные системы (триангуляционные сканеры). Они предназначены для поисков дефектов и измерения диагностической информации, которую можно определить по контуру исследуемого объекта.

Получение диагностической информации сопряжено с задачами распознавания контуров известной формы, которые определяют контрольные (реперные) точки, используемые непосредственно для измерения.

Сигнал, получаемый с триангуляционных датчиков, имеет множество черт, которые делают его похожим на сигналы в системах связи. Однако существует принципиальное отличие между этими сигналами, которое связано с шагом дискретизации и наличием таких преобразований сигнала, которые не позволяют каждому отсчету принятого цифрового сигнала поставить в соответствие отсчеты опорного сигнала (см.

В профильных системах такого соответствия изначально не предполагается, и формирование опорного сигнала является отдельной задачей, которая по вычислительной сложности может быть сравнима с самой задачей обнаружения или оценки параметров сигнала (см. рис. 2).

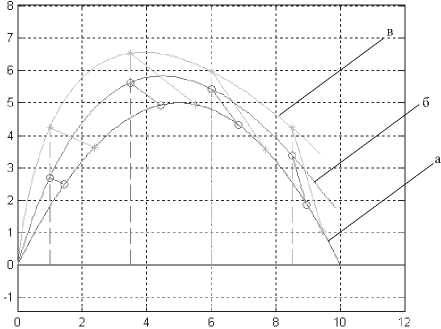
Рис. 2. Соответствие между принятым и опорным сигналом в профильной системе: а) опорный сигнал; б; в) фиксируемый сигнал в профильной системе

Как видно из рис. 2, дискретизация фиксируемого сигнала (см. рис. 2б, в) определяет две несовпадающие последовательности отсчетов на опорном сигнале. Отметим, что большинство работ по тематике распознавания контуров рассматривает в качестве распознаваемых объектов - прямые линии [1-2]. При этом задачи оценки положения сводятся в определению коэффициентов к и b в уравнении прямой z ( x ) = kx + b. Другой крайний случай - это рассмотрение произвольных контуров [3]. В этом случае возможность применения разработанных алгоритмов в силу их сложности и оторванности от предметной области о стается под большим вопросом.

В данной статье предлагается алгоритм оценивания угла поворота для контура, заданного уравнением z ( x ) = Ax ²+ Bx , где A Ф 0, который был разработан с использованием известного приема линеаризации математической модели.

Постановка задачи

Пусть профиль исследуемого объекта определяется аналитическиz(x) = Ax2+Bx, где A Ф 0. В профильной системе фиксируется контур этого объекта z'(/). Известно, что точка (z^X,) на профиле соответствует точке (0,0) профиля объекта, а точка (Z^, Х2) принадлежит этому конуру. Задача состоит в оценке угла поворота а (см. рис. 3). Отме тим, что в общем случае точка (Z!,X[) может не совпадать с какой-либо точкой z’(x')

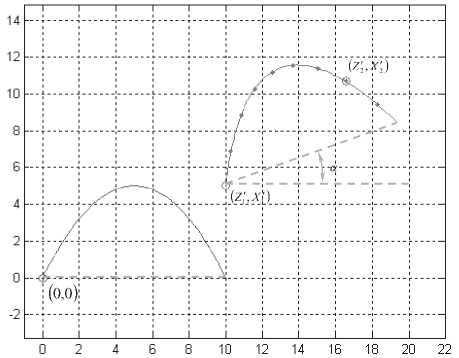
Рис. 3. К постановке задачи оценки угла поворота

Так как точка (z^X,) соответствует точке (О,О), то совмещение фиксируемого контура путем параллельного переноса будет означать, что на контуре точка (Z^,^) перейдет в точку (Zs,Xs): Xs = X₂-Xy Zs = Z₂-Zy Обозначим точку (z,x) координату на контуре z(x) = Ах²+Вх, которая соответствует точке (Zs,Xs).

Линеаризация модели

Запишем систему уравнений, которая связывает точку (Z,X) и (Zs,Xs). Если не учитывать влияние шумовой составляющей, то можно за- писать

Xs = X ■ cos(«)- Z ■ sin(«);

Zs = X • sin(tz) + Z • cos((z)

Так как точка (Z,x) принадлежит контуру, описываемому уравнением параболы, то справедлива запись Z = АХ² + ВХ:

Xs = X -cos(«)-(zx⁹ + ВХу sin(a);

Zs = X • sin(a)+ (AX² + Bx\ cos(a). ⁽2)

Это система уравнений с двумя неизвестными X и а . Для определения этих параметров воспользуемся методом наименьших квадратов:

\Х •cos(tz)-(zx² + ВХу sin(«)}+

[Зй-

+ Zs - (х • sin((z)+ (АХ² + Вх\ cos(ci')}]" ^ min.

Раскрывая скобки, получим:

(%№ - 2Xs • X • cos(a)+ 2Л • Xs • X ² • sin(a) +

+ 2B-Xs-X-sin^a)+A2X4 +2AB-X3 +

+ 5² -X² + Zs² -2X-Zs² -sin(a)-         (4)

- 24 ■ X² • Zs • cos(a)-25 -X ■ Zs - cos(a) +

+ ^2)^min.

Для линеаризации заменим тригонометрические функции приближенными формулами:

cos(a)~ l-0,5a², sin (a)» a.

С учетом этой замены можно записать:

+ 2B ■ Xs ■ X ■ a + A2X4 +2AB ■ X3 +

+ S² -X² +Zs² -2X-Zs² -a-           (5)

-2А-Х² -Zs ■ (1-0,5a²)-

- 2B • X • Zs • (1 - 0,5a²)+ Z² )^ min.

Поиск минимума функции определяет операция дифференцирования по неизвестным параметрам X и a и приравнивания их к нулю. В результате получаем систему из двух уравнений:

• - 2(1 - 0,5a² )• Xs + 4aA ■ Xs ■ X + 2aB • Xs +

+ 44² • X³ + 6AB-X² +2B² -X-2a-Zs-

< -4(1 -0,5a² )a • X • Zs - 2(1 -0,5a² )s■ Zs + 2X = 0; (6) 2a ■ Xs • X ^2A- Xs • X² *2B - Xs ■ X -

• -2-X ■ Zs+ 2aA-X² ■ Zs+ 2aB ■ X ■ Zs = 0.

Из второго уравнения системы (6) можно выделить параметр a и подставить его в первое. Получим уравнение пятой степени от переменной axX5 + bxX4 + cxX3 + dxX2 + exX + f =0, (7)

где ax = 4A2Zs\ bx =8A3-Xs-Zs + ;4A3B-Zs2, cx =18A2B2 Zs2 -4A3Zs3 + 20A2B • Xs • Zx-

• - 2Л³ ■ Xs² ■ Zs + 4Л² • Xs² + 2A² ■ Zs²

dx =16AB2-Xs-Zs + 4AB-Zs2 +6AB-Xs2 +

+ 4A-Xs-Zs-3A2Xs3 -10A2B-Zs3 -

• -8Л² -Xs-Zs² -5A²B-Xs² • Zs + 10AB³ • Zs², e_x = -4AB² • Xs² • Zs - 4AB • Xs³ -

  -12AB-Xs-Zs² +4B-Xs-Zs + 2Xs² -

  -4A-Xs²Zs-8AB² -Zs³ +2B⁴ • Zs² +

+ 2B2 Zs2 +4S3-Xs-Zs^2B2 • Xs2, fx =-2B3-Zs3-Xs-Zs2-4B-Xs2 • Zs-

-B2-Xs3-2Xs3-B3-Xs2-Zs-B-Zs3 -

-4B2-Xs-Zs2.

Решая данное уравнение (например методом Лягерра), определяются корни переменной X , а из второго уравнения системы (6) – параметр a . Из этих параметров выбирается то значение, при котором достигается минимум функции (3).

Если угол a не является малым, то может потребоваться проведение нескольких итераций. На рис. 4 показан пример итерационной работы алгоритма.

Заключение

В работе представлен алгоритм оценки поворота контура, заданного в виде уравнения параболы. Для этого частотного случая была найдена аналитическая формула при условии, что известна опорная точка, которая обозначена в статье как (ад) . Допущение, что она может быть известна, может быть верно только в частных случаях.

Дальнейшим обобщением данной работы будет исследование и разработка алгоритма при условии, что опорная точка (г;л;) известная

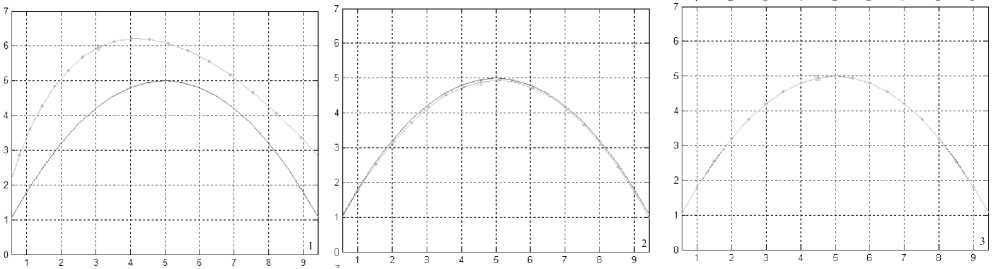
Рис. 4. Пример совмещения контуров по разработанному алгоритму: цифрой обозначен номер итерации

с некоторой точностью (az, аг), чтобы он как можно более полно мог удовлетворять задачам практических приложений.