Оценивание влияния ошибок модели движения астероидов, сближающихся с Землей, на точность построения доверительных областей

Введение. Современный мир подвержен многим опасностям различного характера, и даже такой, как столкновения малых тел Солнечной системы с Землей или космическими аппаратами [1; 2]. Для приближенной оценки этой угрозы используется вероятностный метод определения орбит небесных тел. Так как наблюдения астероидов отягощены неизбежными ошибками, мы можем получить из них только некоторую оценку их возможных параметров. Эта оценка определяет номинальную орбиту малого небесного тела. Чем больший интервал будет охвачен наблюдениями, тем точнее и ближе она будет к истинной траектории объекта. Поэтому для достоверности расчетного движения астероида целесообразно описывать его плотным пучком траекторий, выходящих из начальной доверительной области. И далее, для исследования движения небесного тела, производить отображение этой области на любой другой момент времени. Известно также, что систематические ошибки наблюдений и модели движения астероидов могут оказывать существенное влияние на точность построения доверительных областей. В случае, если эти ошибки достаточно большие, может оказаться, что реальное движение изучаемого объекта будет вне расчетной области возможных движений. Это особенно неприемлемо при исследовании возможных столкновений астероидов с Землей или космическими аппаратами. Исключение систематических ошибок из наблюдений представляет собой сложную и часто неразрешимую задачу, и этой проблеме посвящено достаточно много работ [3-6]. В настоящей работе приводится полный алгоритм способа, позволяющего анализировать модели движения астероидов при построении доверительных областей. Выбор же модели возмущающих сил в традиционно применяемых методах связан только с анализом их влияния на точность определения номинальной орбиты объекта. Размеры доверительных областей в этих оценках не учитываются. Рассматриваемый нами способ этот недостаток устраняет, и выбор модели возмущающих сил этим способом тесно связан с размерами доверительных областей и смещениями оценок параметров орбит, определяемых для альтернативных моделей движения исследуемого объекта.

Задача построения доверительной области. При построении начальной доверительной области движения астероида нужно указать вероятность попадания истинного значения определяемых параметров в область их оценок

P { q t ^е Q ( ^q / d * ) } ^ Y, ⁽¹⁾

где q _t — истинная (неизвестная нам) точка в m -мерном пространстве определяемых параметров q = ( q 1 , q ₂, ..., q m ); q — оценка этих параметров, определяемая по n -мерной выборке измерений d * = ( d * , d 2 ,..., d n ) ; Q ( • ) — доверительная область; число y — коэффициент доверия, показывающий, с какой вероятностью область Q ( • ) накрывает m -мерную истинную точку q _t .

Оценка q находится из решения задачи наименьших квадратов (НК):

Ф ( q ) = [ d(q) - d* J T W [ d(q) - d* ] = min, (2) где O ( q ) — целевая функция задачи наименьших квадратов; d(q) — расчетная n -мерная вектор-функция измеряемых параметров; W — весовая матрица; символ T означает операцию транспонирования.

Линейные методы построения доверительных областей. В линейном случае наименьшие по размерам начальные доверительные области представляют собой 6-мерные эллипсоиды, определяемые выражением

( q - q ) ^T [ R ^t ( q ) WR ( q ) ] ( q - q ) = s . (3) Здесь

8 = ^ 0 ( k Y )², (4) где n₀ = [ O ( q )/( n - m ) ] ^1/2 — среднеквадратическая ошибка единицы веса; R(q ) = d d(q ) / d q — матрица частных производных размером n^m ; величина k _Y оценивается с помощью статистик F ( m ; n - m )-распре-деления Фишера в виде

( k _Y )² = mF ( m ; n - m ; y * ). (5)

Величина F ( m ; n - m ; y*) = F * есть верхняя квантиль для F ( m ; n - m ^распределения .

Доверительные эллипсоидальные области представляют собой области возможных значений параметров орбит с граничной поверхностью, накрывающей с заданной в линейном приближении вероятностью истинные значения параметров орбиты объекта.

При построении области по ее граничной поверхности точки, заполняющие эллипсоид, можно находить при помощи алгоритма [7—9]

q j * = q +T k n- a n J . (6) ⁿ j l

Здесь вектор n_j = (n₁,П₂, ■■■,П m ), компоненты которого n i e N (0;1) — независимые нормально распределенные случайные числа с единичной дисперсией; j = 1,2, ..., 5 , где s - количество точек q j * , определяемое длиной моделируемой датчиками случайных чисел выборки вектора n j ; A — нижняя треугольная матрица, такая, что AA = D ; D - НК-оценка ковариационной матрицы, определяемая выражением

D = ^0 [RT (q)WR(<7)]-1■(7)

Моделирование случайных точек qj* при помощи алгоритма (6) должно удовлетворять условию е7 < е , где

• (q,* - q)T[RT (qW(q)](qy* -q) = 8j ■(9)

Построение доверительной области в нелинейном случае. Если нелинейность связи между вероятностными вариациями ошибок наблюдений и начальных параметров значительна, то формальное определение ковариационной матрицы и задание по ней эллипсоидальной доверительной области становится неправомерным^ В этом случае приходится применять трудоемкие многократные решения задачи НК вида [10] Ф ( q ) = [ d ( q ) - d * - 6 d J W [ d ( q ) - d * - 6 d ] = min (10)

или

Ф( q ) = [ d ( q ) - d ( q ) - 6 d ] T W [ d ( q ) - d ( q ) - 6 d ] = min (11)

Здесь 6 d e N (0, g0) — независимые нормально распределенные случайные числа с дисперсией, определяемой из решения исходной задачи НК (2),

Найденная таким образом доверительная область представляет собой множество оценок q ^j и имеет, как правило, неправильную бананообразную форму■ Ее граничную поверхность мы предлагаем определять уравнением [8; 9]

Ф ( q ) = C ,                    (12)

где Ф( q ) - целевая функция задачи НК (2)-

В качестве постоянной C можно выбрать C = ФF , а также любое из близких друг к другу значений целевой функции в нескольких различных вершинах доверительного эллипсоида или их среднеарифметическое значение, так как близкие значения целевой функции однозначно указывают на то, что эти вершины лежат в окрестности граничной поверхности^ Целевая функция ФF, определяющая граничную поверхность доверительной области, находится при помощи соотношения ФF =Ф(q)(1 + kY / (n - m)) ■

Алгоритм сравнения моделей движения. Сравнение моделей возмущающих сил и выбор лучшей модели в задаче построения областей возможных движений астероида осуществляется нами при помо- щи следующего показателя [3; 7; 11]:

ε отн

A d = |^q * ^{- q}| d |q ^- q|

где q* и q - оценки параметров орбиты объекта, определяемые задачей наименьших квадратов по данной (одной и той же) n-мерной выборке измерений d* с использованием двух моделей сил F* и F ; q - точ- ка, лежащая в параметрическом пространстве вдоль направления q* - q на уровенной поверхности дове

Г

1 +

рительной области Ф F = Ф ( q )

( k Y )²

n - m

Очевидно, что значения еотн > 1 (т е_ Ad > d) определенно указывают на большие смещения относительно друг друга НК-оценок параметров q* и q (следовательно, и доверительных областей, построенных на основе этих оценок) Если же еотн < 1 (т е_ Ad < d), эти смещения можно считать малыми по сравнению с размерами доверительных областей только при выборе более жесткого критерия, такого как, например, еотн < 0,L Наглядное представление такого способа оценивания влияния возмущающих сил на точность построения областей возможных движений астероидов с использованием показателя еотн дает рис 1 ■

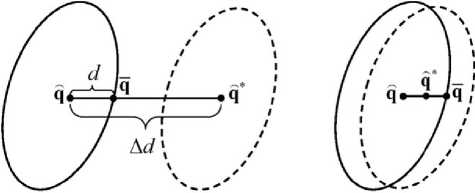
A d >  d                      A d <  d

Рис 1 Геометрическое изображение оценивания смещения доверительных областей по показателю еотн

В случаях, когда имеют место сближения астероидов с Землей или другими планетами, этот критерий необходимо уменьшить еще на несколько порядков^ Следует также отметить, что рассматриваемый способ анализа модели движения астероидов может быть применен как для построения начальных областей возможных значений параметров орбит, так и при отображении этих областей во времени В зависимости от степени нелинейности задачи для определения в параметрическом пространстве точки q , можно применять линейный либо нелинейный метод нахождения точек граничных поверхностей доверительных областей [3; 11; 12]^ При слабой нелинейности линейный метод может быть реализован следующим алгоритмом:

k q = q +        A ( q - q ) T ■           (14)

Iq - ql

В случае, если доверительную область нельзя аппроксимировать эллипсоидом, то находим точку q _n, решая нелинейное уравнение

F ( q ) = Ф ( q ) -Ф f = 0,            (15)

где q = q + l ( q * - q ); l - параметр растяжения (сжатия) вектора q * - q до граничной поверхности.

Схема решения уравнения (15) методом Ньютона может быть записана в виде следующего алгоритма:

[ ^F ( q ) ] i = i n