Оценка амплитуд "наложившихся" масс-спектрометрических пиков при известных положениях на оси масс и известных полуширинах алгебраическим методом

Рассмотрены возможности алгебраического метода восстановления амплитуд "наложившихся" масс-спектрометрических пиков при известных положениях и полуширинах. В основе рассмотренного метода лежит решение методом наименьших квадратов системы линейных уравнений, в которой количество неизвестных равно количеству пиков в спектре, а количество уравнений равно количеству измеренных отсчетов в спектре. Приводятся результаты исследования метода на математических моделях масс-спектра. Показаны возможности оценки амплитуд масс-спектров примесей с массой, близкой по массе пика основного продукта. Для эффективной работы метода необходимо предварительное проведения операций сглаживания и фильтрации, с помощью которых отношение сигнала к шуму должно быть больше 500.

ПОСТАНОВА ЗАДАЧИ

В изотопном масс-спектрометрическом анализе примесей основного продукта на предприятиях ядерно-топливного цикла существуют задачи, когда массы примесей априори точно известны и требуется оценить по результатам эксперимента точное значение амплитуд пиков. При этом из-за недостаточного разрешения масс-спектрометра некоторые пики могут быть "наложившимися", но в то же время полуширины этих пиков известны по априорным результатам оценки разрешающей способности прибора. Предлагается алгебраический метод решения обратной задачи [1], позволяющий сделать оценки амплитуд "наложившихся" пиков масс-спектра. В предлагаемом методе использован подход к обработке Оже-спектров, описанный в работе Ю.А. Демина и других [2], но модифицированный в соответствии со спецификой измерений в изотопной масс-спектрометрии. Кроме того, предложен отсутствующий в работе Ю.А. Демина способ решения переопределенной системы уравнений. Предлагаемый алгебраический метод решения обратной задачи может быть применен также для восстановления параметров масс-спектров и других спектральных сигналов, очищенных от шумов.

ОПИСАНИЕ АЛГОРИТМА

Пусть каждой i -й массе спектра, по которому производится анализ, соответствует нормированный эталонный спектр Spi (m). Пусть количество анализируемых масс равно N, а количество отсчетов спектра равно M. Тогда результирующий масс-спектр (без учета фона) можно описать произведением матрицы размерности M х N, состоящей из столбцов — эталонных спектров отдельных масс, на вектор-столбец размерности N, представляющий собой амплитуды искомых пиков. Таким образом, приравняв расчетный суммарный спектр экспериментальным данным ESp (m), получим переопределенную (при N << M) систему линейных уравнений:

S M m l ) ^SP 2 ⁽ m l ) - ^S P n ⁽ m l ) Sp ( m 2 ) Sp 2 ( m 2 ) - SP n ( m 2 )

. SP l ^{( m} M ) SP 2 ^{( m} M ) - ^S P n ⁽ m M )

ESp ( m _l) ESp ( m ₂)

. ESP ^{( m} M )

A l A

AN

(l)

Приближенное решение такой системы можно выполнить методом наименьших квадратов [4].

В выражении (l) Sp _l( m r )— значение r -отсчета пика единичной высоты с массой m _l; ESp ( m r ) — значение r -отсчета в зарегистрированном экспериментальном спектре. Сумма квадратов невязок имеет вид:

M

X[ SP1( mr ) A + Sp 2( mr ) A2 + - + SPN ( mr ) AN - ESP (mr )]2.(2)

r = 1

Если Ar таковы, что эта сумма минимальна, то d f M1

SP1( mr ) A1 + SP 2( mr ) A2 + "' + SPn (mr ) AN - ESP(mr )] f = 0- dAr I

Дифференцирование дает систему из N линейных уравнений с N неизвестными. i -уравнение системы имеет вид

M

£ [ SP 1⁽ m r ) ^SP i⁽ m r ) A 1 + SP 2 ⁽ m r ) ^SP i⁽ m r ) A 2 + "• + SP N ⁽ m r ) ^SP i⁽ m r ) A N - ^SP i⁽ m r ) ^ESP ⁽ m r ) ] = ⁰ '    ⁽⁴⁾

r = 1

В общем виде такую систему можно записать так: С • A = B , где A — вектор неизвестных, С — матрица коэффициентов при неизвестных, а B — вектор свободных членов. Выделяя из (4) вектор свободных членов, получаем, что i -й элемент этого вектора равен

M

B ⁽ i ) = X SP i ( m r- ) ESP ⁽ m r )•         ⁽⁵⁾

r = 1

Каждый элемент матрицы C при неизвестных A_r вычисляется по формуле

M

C ⁽ i , j ) = X SP i ⁽ m r ) SP j ⁽ m j );        ⁽⁶⁾

r = 1

i , j — соответственно номер столбца и строки матрицы C .

Система из N линейных уравнений типа (6) с N неизвестными решается методом Крамера.

ПРОВЕРКА АЛГОРИТМА НА МОДЕЛЯХ МАСС-СПЕКТРА

Получение масс-спектра путем умножения матрицы эталонных спектров на вектор-столбец амплитуд

Первым шагом проверки алгоритма являлось решение прямой задачи, т. е. по известным эталонным спектрам и заданным амплитудам получение модели масс-спектра.

Пусть количество анализируемых пиков изотопного масс-спектра N = 5, а количество точек в экспериментальном масс-спектре M = 1500. Для получения эталонного масс-спектра будем считать, что ширина спектральных линий для всех масс одинаковая и равна < 7 = 0.30.

Нормированная спектральная линия описывается выражением:

M

SP ⁽ m i ) = X exp '

r = 1

⁽ m r - m i 1 ²

,

где m_i — значение i -й массы, r — номер точки в масс-спектре.

На рис. 1 представлен эталонный нормированный спектр для m_i = 338.

Выполнив умножение матрицы из столбцов нормированных масс-спектров на вектор из амплитуд заданных масс в соответствии с правой частью выражения (1), получаем модель масс-спектра, представленную на рис. 2. В данной модели: вектор амплитуд A = [328, 44, 1026, 1151, 391], вектор положений пиков на оси времени (масс) Tp = [338, 340, 340.001, 341, 343].

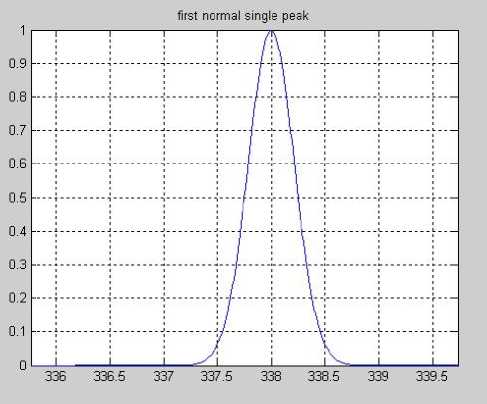
Рис. 1. Нормализованный пик с центром на оси масс 338 и полушириной 0.3 на полувысоте

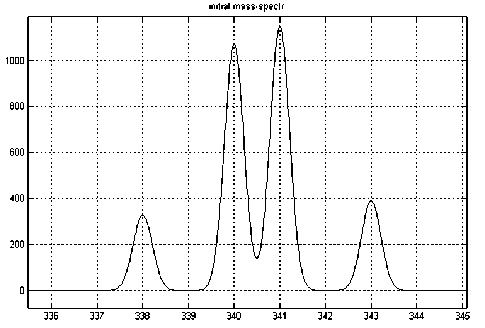
Рис. 2. Модель масс-спектра из 5 линий после умножения матрицы эталонных нормированных спектров на вектор амплитуд (на массе 340 — "наложившиеся" пики, рассмотренные ниже)

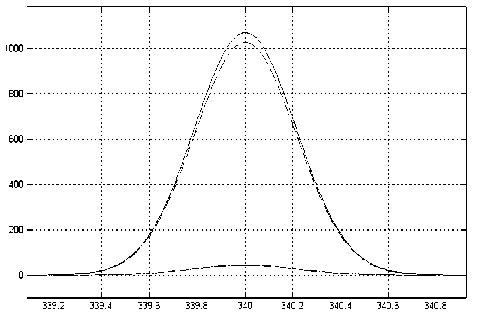
Рис. 3. Фрагмент масс-спектра в районе массы 340 для примера 1. Пунктирная линия соответствует пику на массе 340.001, а сплошная линия малого сигнала пику на массе 340.000

Результирующий масс-спектрометрический сигнал записывается в виде следующего выражения:

5     1500

ESp ( m ) = S A S exp ’ i = 1       r = 1

( m r - m i 0.3

Восстановление вектора амплитуд при практически отсутствующем шуме

Пусть известны:

• •    вектор длиной M = 1500, представляющий собой зарегистрированный масс-спектр;

• •    вектор длиной N = 5, представляющий собой набор масс измеренного изотопного масс-спектра.

Кроме того, заданы N векторов длиной M , представляющие собой нормированные эталонные спектры. Произведя вычисления коэффициентов C ( i , j ) согласно формуле (6) и вектора свободных членов по формуле (5), получим систему из N линейных уравнений с N неизвестными.

Система решается методом Крамера следующим образом.

• 1.    Вычисляется определитель D системы из матрицы коэффициентов C ( i , j ).

• 2.    Столбец 1 матрицы C заменяется вектором свободных членов и вычисляется определитель ^D 1 ^.

• 3.    Заменяя последовательно столбцы 2, 3,…, N матрицы C вектором свободных членов вычисляются определители D ₂ , D ₃ ,…, D_N .

• 4.    Амплитуды пиков A ₁, A ₂, … , A_N с массами m ₁ , m ₂ ,…, m_N изотопного масс-спектра вычисляются по формулам:

A i = D)'’ A 2 = Dd^; -^; An = D •       (8)

Пример 1

Пусть вектор масс представляет собой набор следующих чисел:

mp = [338, 340, 340.001, 341, 343]

(2-е и 3-е массовые числа отличаются на 0.001).

На рис. 3 представлен фрагмент масс-спектра в районе массы, равной 340. Произведя вычисления по формулам (8), получаем вектор амплитуд А = = 1.0E+003×[0.3280, 0.0440, 1.0260, 1.1510, 0.3910]. Данный вектор в точности соответствует заданным амплитудам в исходной модели.

Пример 2

Пусть вектор масс представляет собой набор следующих чисел:

mp = [338, 340, 340.0001, 341, 343]

(2-е и 3-е массовые числа отличаются на 0.0001).

Произведя вычисления по формулам (8), получаем вектор амплитуд А = 1.0E+003×[0.3280, 0.0440, 1.0260, 1.1510, 0.3910], не отличающийся от заданных амплитуд на исходной модели.

Из примера 2 видно, что при отсутствии шума вычисления амплитуд остаются безошибочными при разности масс между "наложившимися" пиками 0.0001.

Оценки амплитуд А ₂, А ₃ пиков с близкими массами в присутствии шума

№ эксперимента	σ шума	А 2 (масса 340)	А 3 (масса 340.001)
1	0.001	43.6	1026.4
		44.2	1025.8
		44.0	1026.0
2	0.01	44.1	1026.0
		43.6	1026.4
		44.0	1026.0
3	0.02	46.2	1023.8
		43.9	1026.1
		43.5	1026.5
4	0.04	45.2	1024.8
		43.8	1026.2
		44.3	1025.7
5	0.08	44.0	1025.9
		44.1	1025.9
		41.1	1028.9

Пример 3

Исходные данные, как в примере 2, но расстояние между 2-м и 3-м пиками 0.00005. Получается вектор амплитуд А = 1.0E+003×[0.3280, 0.0442, 1.0258, 1.1510, 0.3910]. Как видно, появляются отличия в четвертом знаке.

Пример 4

Исходные данные, как в примере 3, но расстояние между 2-м и 3-м пиками 0.00001. Получается вектор амплитуд А = 1.0E+003×[0.3280, 0.0319, 1.0399, 1.1510, 0.3910]. Как видно, отличия в определении амплитуды малого пика в "наложившихся" пиках составляют примерно 25 %. Дальнейшее сближение пиков не имеет смысла, т. к. начинает сказываться неточность вычислений. В данных модельных экспериментах неточность вычислений соответствовала единице в восьмом десятичном знаке. Действие неточности вычислений аналогично наложению шума.

Оценка амплитуд пиков близких масс изотопного масс-спектра в присутствии шума .

Для условия задачи, представленного выше, произведем оценку амплитуд для пиков с близкими массами, т. е. для пиков с массой 340 и 340.001 в присутствии шума.

Результаты расчетов представлены в таблице. Как видно из таблицы, при увеличении среднего квадратичного значения шума погрешность оценки амплитуд пиков близких масс возрастает. Для значения σ_шума = 0.08 погрешность оценки амплитуды малого пика составляет 2…3%. Значение указанной погрешности определено из серии, состоящей из более чем 15 численных экспериментов.

Во всех результатах численных экспериментов количество точек модельного масс-спектра оставалось постоянным и было равно 1500.

При увеличении количества точек модельного масс-спектра до 15 000 погрешность оценки амплитуд уменьшалась примерно в 1.5…2 раза.

ВЫВОДЫ

Предложен метод оценки амплитуд "наложившихся" пиков изотопного масс-спектра, в котором известны массы и разрешающая способность. Данный метод основан на составлении и решении переопределенной системы линейных уравнений, в которой число уравнений равно количеству точек зарегистрированного масс-спектра, а количество неизвестных равно числу исследуемых масс. Проверка данного метода на моделях масс-спектра при практически отсутствующем шуме позволяет производить оценку амплитуд "наложившихся" пиков при разнице в массовых числах 0.00005 для массового числа 340. При наличии шумов данный метод позволяет производить оценку амплитуд "наложившихся" пиков при разнице в массовых числах 0.001 с погрешностью 2…5 процентов при отношении сигнал/шум 500 и выше для массового числа 340. Применение данного метода целесообразно для сигналов, для которых предварительно выполнены операции фильтрации и сглаживания.