Оценка близости моделей наблюдаемой навигационной ситуации как многокритериальных объектов с вероятностными приоритетами

Обеспечение безопасности мореплавания возможно при условии постоянного и правильно организованного наблюдения за окружающей обстановкой, которое должно вестись в соответствии с Международными правилами предупреждения столкновений судов в море (1972 г.); таким образом оценивается навигационная ситуация и при ее осложнении выполняются немедленные и надлежащие действия. Лицо, принимающее решение (ЛПР, вахтенный помощник капитана), может оставаться единственным наблюдателем при условии, что навигационная обстановка безопасна и полностью учтены все сопутствующие плаванию опасные факторы. На судах имеется возможность немедленного усиления вахты на мостике в случае, когда этого потребуют обстоятельства ( Гладышевский и др. , 2008; Анисимов и др ., 2009).

При решении задач по обеспечению безопасности плавания судна ЛПР обязано максимально эффективно использовать все имеющееся в его распоряжении навигационное оборудование и оценивать близость наблюдаемых моделей навигационной обстановки в рамках индивидуальной структуры предпочтений. В общем случае идентификация моделей навигационной обстановки позволяет ЛПР принимать "работающие решения" по обеспечению безопасности плавания судна с ориентацией на принцип "наилучших намерений" ( Марковский и др ., 2013). Целью нашего исследования является составление вероятностной оценки отношения близости наблюдаемых моделей навигационной ситуации, полученных на базе информации, поступающей лицу, принимающему решения, по двум независимым каналам: системе кругового визуального обзора (СКВО) и информационной навигационной системе.

2.    Вероятностная оценка отношения близости двух моделей навигационной ситуации

Принципиальная структурная схема системы наблюдения за окружающей навигационной обстановкой (см. рис.) включает систему кругового визуального обзора, информационную навигационную систему, отображающую текущую навигационную ситуацию, и лицо, принимающее и обрабатывающее поступающую информацию и выбирающее решение.

При использовании системы наблюдений ЛПР должно соблюдать положения Международных правил предупреждения столкновений судов в море (1972 г.) ( Гладышевский и др. , 2008; Анисимов и др ., 2009). В соответствии с этими положениями будем считать, что модели навигационной ситуации O_ν , поступающие к судоводителю из СКВО и информационной системы, можно представить в виде графа подобия, причем две вершины этого графа T_νC'_iν и C'_kν сравнимы ( Вагнер , 1972). Тогда близость моделей ситуаций как многокритериальных объектов можно оценить на вероятностном уровне. Для этой цели принимаем исходное предположение о том, что оценки моделей навигационной ситуации O_ν , равные C_i и C k , с равной вероятностью могут соответствовать любой из оценок по принятым шкалам используемых критериев в рамках структуры предпочтений ЛПР.

Пусть шкала j- го критерия имеет t оценок (первая – худшая, t- я – лучшая), а оценка O ν^j = l. Тогда

Попов Ю.А. и др. Оценка близости моделей...

возможны случаи расположения оценок O_v C i и C k на шкале j- го критерия, при которых оценка C i выше оценки C k или равна ей. Очевидно, что четыре аналогичных случая соответствуют тому, что оценка C k выше оценки C i или равна ей. Кроме того, можно выделить случай, когда оценки C i и C k выше оценки O_v . Тогда ( Вагнер , 1972)

C' i v j = C' kvj = O .

Случаи, соответствующие описанным событиям, отражают доминирование оценки C i над оценкой C k . Поэтому в общем случае возможны три следующих альтернативы:

• -    оценки совпадают: C' i _v j = C'_{k v} j ;

• -    оценка C'i _v j доминирует над оценкой C kj ;

• -    оценка C'_{k v} j доминирует над оценкой C' i _v j .

  

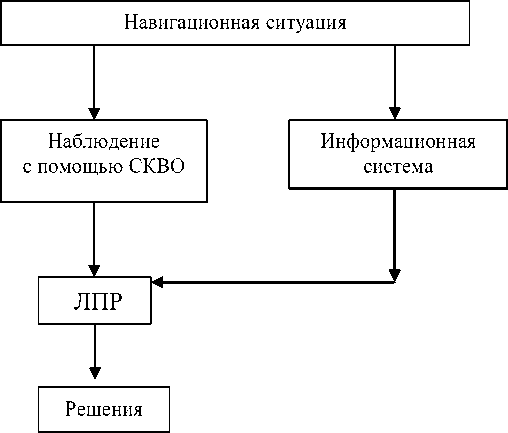
Рис. Принципиальная структурная схема системы наблюдения за окружающей навигационной обстановкой

Используем обозначения: B - число всех возможных вариантов, соответствующих первой альтернативе; D - число всех возможных вариантов второй альтернативы; F - число всех возможных вариантов третьей альтернативы. Учитывая равенство вероятностей из условия O V = l , найдем:

B = ( t - l + 1)² + ( l - 1),

D = [( l - 1)( l - 2) + ( t - l + 1)( l - 1)] / 2, F = [( l - 1)( l - 2) + ( t - l + 1)( l - 1)] / 2.

В общем случае, когда l меняется от 1 до t , получим:

tt в (t) = Z (t -1 + 1)2 + Z (l -1), i = 1

tt

D(t) = [Z(l - 1)(l - 2) + Z (t -1 + 1) (l - 1)] / 2, i = 1

tt

F ( t ) = [Z ( l - 1)( l - 2) + Z ( t - 1 + 1) ( l - 1)] / 2.

i = 1

Число всех возможных альтернатив Е ( t ) = t ³. Тогда вероятность того, что модели навигационных ситуаций C'_iv и Ck, будут обладать одинаковыми оценками по критерию j , равна ( Акофф, Сасиени , 1971)

p о = B ( t ) / E ( t ) = {Z [( t - l + 1)² + ( l - 1)]} / 1 ³.

i = 1

Вероятность того, что модель навигационной ситуации C'_iv доминирует над моделью C' kv по критерию j , равна ( Акофф, Сасиени , 1971)

tt pi = D(t) / E(t) = {[К(1 - 1)(1 - 2) +К (t -1 + 1)(1 - 1)] / 2} /t3.

i = 1

Аналогично вероятность доминирования модели ситуации C'kv над моделью Civ равна tt p2 = F(t) / E(t) = {[К (1 - 1)( 1 - 2) + К (t - 1 + 1)( 1 - 1)] / 2} /t3.

i = 1

Очевидно, что p ₀ + p 1 + p ₂ = 1 и p 1 = p ₂. Тогда при нескольких критериях оценки моделей навигационных ситуаций в соответствии с бинарным отношением В 1 возможны следующие ситуации:

• -    модели ситуаций С„ и C'_kv близки (оценки C'_iv по всем критериям больше или равны оценкам C'kv или наоборот),

• -    модели ситуаций C'_iv и C' kv находятся в отношении неблизости (по одним критериям C i _v доминирует над C'kv , а по другим - наоборот).

Подсчитаем вероятность того, что модели ситуаций C'iv и C'kv близки для общего случая, когда имеется п критериев: nn

Р (n) = р 0 ” + I СПр 0 n- ip 11 +I СПр 0 n- ip 21,(1)

i = 1

где С П - число сочетаний из п по 1 .

Первый член в выражении (1) есть вероятность того, что модели навигационных ситуаций близки, второй член - вероятность того, что первая модель навигационной ситуации доминирует над второй, а третий член соответствует вероятности того, что вторая модель навигационной ситуации доминирует над первой.

Определим вероятность того, что по ( n - 1)-му критерию оценки одной модели ситуации равны оценкам другой модели ситуации (или выше их), а по 1-му критерию вторая модель ситуации доминирует на первой моделью (неблизость по 1-му критерию):

n - 1

Q(n) = Cn1C1 n -1 p0n - 2 p 1 p2 + К Cn1C1 n -1 p0n -1 -1 p 1 p2 + К Cn1C n -1 p0n -1 -1p 1 p21.(2)

i = 2

Подсчитаем вероятность неблизости по двум критериям, т. е. вероятность того, что по ( n - 2)-м критериям оценки одной модели навигационной ситуации равны оценкам второй (или выше их), а по двум критериям вторая модель доминирует над первой моделью:

n - 1

U(n) = Cn2C2n - 1 p0n - 4p 12 p22+ К Cn2Cn - 2 p0n - 2 - 1p 11 p22+ К Cn2C n - 2 p0n - 2 - '1p 12 p2'

1 = 3

Таким образом, выражения (1-3) позволяют с вероятностной точки зрения идентифицировать наблюдаемые модели навигационной ситуации в отношении их близости и принять "работающее" решение с акцентом на реализацию принципа "наилучшего намерения", который способен обеспечить безопасность и эффективность плавания судна.

3.    Заключение

При решении задач по обеспечению безопасности плавания судна необходимо максимально эффективно использовать все системы наблюдения за окружающей обстановкой и оценивать близость наблюдаемых моделей навигационных ситуаций в рамках индивидуальной структуры предпочтений.

В общем случае идентификация моделей навигационной обстановки позволяет ЛПР принимать "взвешенные и работающие" решения, обеспечивающие безопасность и эффективность плавания судна в рамках принципа "наилучших намерений".