Оценка быстродействия динамического процесса на классе дифференцируемых функций с ограничениями

Пусть W ² означает класс заданных на всей числовой прямой R действительных дифференцируемых функций f ( t ) с абсолютно непрерывной производной f ( t ) на любом отрезке из R и нормой Чебышева функции и ее производных:

II fl I = sup| f (t )V If' I = sup| f'(t )|, If" I = ess sup| f" (t )| (-” < t < ”).

Введем следующие обозначения: M = || f ||, L = || f ||, K = || f ||.

Задача быстродействия динамических процессов и систем давно изучается в различных математических разделах, в том числе в теории управления, в теории динамических систем (см., например, [4]). Рассмотрим следующий вариант этой задачи: найти наименьший промежуток т изменения аргумента t , на котором процесс f ( t ) переходит с уровня – М на уровень М при ограничениях

Il f l< M |f "k K

В теории аппроксимации функций хорошо известно неравенство Адамара [6], связывающее числа M, L, K :

L <  7 2 MK .                               (1)

Отметим, что А.Н.Колмогоров [2, 3, 5] получил точные оценки норм промежуточных производных действительных дифференцируемых функций с ограничениями на норму самой функции и ее старшей производной в более общем случае. А именно, пусть f е W^r ( r=2, 3, ... ) и при некотором 1>0 выполнены ограничения || f ||< || ^ _1r |, || ^^{( r} )||< 1, где Ф _г1 ( t ), ( r = 2,3,...) — сплайны Эйлера.

1 _{г х} л 1 у ч 4 sin((2 к + 1) t + n r /2)

9 r1 ( t ) = -f r ( lt ) ( r = ^0,1,2) f r ( t ) = -S _vxr + 1 ------        (2)

^{1                                  п} к = 0       ⁽² k + 1)

Тогда имеет место точное неравенство:

II f ( k ’ll< 9 - k , ' ll ( k = 1-2,...- r - 1).

Нетрудно заметить, что

/Xt ) = f, - , ( t ) ( r = 1-2-...), а также

9,i( t) = 9r-u (t) (r = 1-2-...).(3)

Рассмотрим функцию

921 (t’ = К f2(lt ’   .(4)

Параметр l в формуле (4) всегда можно подобрать так, чтобы выполнялось равенство

II92 ill = К If21 = M.(5)

Действительно, нормы сплайнов Эйлера или, по-другому, констант Фавара, известны и равны

A ”   ( i ^; '^{( r + 1)}

K r =1 f r ll = ~ X З^^ +г    ( r = 0^-1-2-...).

^п j , 0 ⁽² j + 1’

В частности,

K = 1- K = - - K = — . 0           1 2        2 8

Таким образом- || 9 2 1 || = К\|^f 2|| = КK 2

К П

8 l ²

= M . Из этого равенства получаем

1 =

П К

2 2 M ^.

Подставляя это выражение в (3), находим

8 M , , nXK

^{9 2 1 (} ' ’ п ^{2 f !}(2V2 M ' ’^-

2^2MK   П К            П К .

9 1 1 ⁽ t ’ =        f ^{1 (}^2 M t ’.    9 о i ⁽ t ’ = ^Kfо^ t ’.

Нормы полученных функций таковы:

II 9 2 1 1 = M 9 1 i ll = V2 MK 9 o 1 || = К .

Это означает- что на сплайне 9 ₂ l ( t ) реализуется равенство в неравенстве (1)- следовательно- и максимальное значение нормы производной функции f ( t ) е W ² . С учетом (3)

имеем sup|f'(t’| = |921'|| = |91111 = V2MK . t е R

Назовем тройку чисел ( M, L, К) допустимой относительно функции f ( t ) е W ² -если эти числа связаны неравенством (1)- а именно- L <  V2 MK - где ||f 11 = M - ff = L - || f || = K . Например- тройка ( 2, 2, 1 ) допустима- а тройка ( 1, 2, 1 )

недопустима.

Рассмотрим три случая: 1) L = V2 MK , 2) L > ^ 2 MK , 3) L <  V2 MK .

Пусть L = ^2MK . Тогда наименьший период т быстродействия процесса легко определяется, например, из (6) c помощью теоремы сравнения [1]. В самом деле, наименьшее значение функции f 2 (t) достигается в точке t=0, а наибольшее в точке t = п. Таким об разом, с учетом коэффициента сжатия l получаем следующую нижнюю оценку периода быстродействия:

т = 2

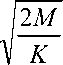
Пусть L > V2MK . В этом случае граница L изменения производной f (t) недости- жима, а значит, в соответствии с неравенством Адамара оценка периода быстродействия остается прежней, т.е. определяется по формуле (7).

Наконец, пусть L <  2 MK . Ясно, что такое ограничение изменения производной приведет к увеличению периода быстродействия процесса. Для нахождения длины этого периода рассмотрим следующую функцию сравнения:

Vn ( t ) = Ks, ( It ) ( r = 0,1,2), где сплайн s , ( It ) ( r = 0,1,2) и его производные определяются так:

' Kt ,

s 1 ( t ) = ) L ,

s 2 ( t ) = <

I- K ( t - т ),

K--M , 2

^L ( t - f),

M - K (L^ L

,

0 <  t <  О

т - О <  t <  т

0 <  t <  О f K , О <  t < т - О s ₀( t ) = ^ 0,

т-О< t <т

- K ,

0 <  t <  О

О <  t < т - О т-О< t <т

Параметры О и т находятся из условий гладкости сплайна дефекта 1 , т.е. непрерывности s ₂ ( t ) и его производной s 1 ( t ):

K О = L ,

О2          „ т

K--M = LО - L -

.

Отсюда получаем следующую оценку быстродействия процесса f ( t ) е W ² :

L ² + 2 MK т =-------- LK

.

Отметим, что если L >  V2 MK (а это случаи 1 и 2 ), то оценка быстродействия (11) переходит в ранее найденную оценку (7).

Нетрудно установить, что оценка (11) не меньше оценки (7):

L ² + 2 MK „ /2 M

.

--------> 2J---

LK K

Это означает, что существенное ограничение изменения производной L <  2 MK приводит к увеличению периода быстродействия процесса.

Действительно, если это не так, то

L ² + 2 MK „ 2 Ш

--------< 2J--- LK K

L ² + 2 MK <  2 L ^ 2 MK

( L - V 2 MK )² <  0.

Полученное противоречие доказывает справедливость неравенства (12).