Оценка численности населения Кубани в 1930-1940-е гг. с использованием методов статистического моделирования

Материал подготовлен при финансовой поддержке Российского фонда фундаментальных исследований, проект № 11-06-00346-а.

Анализ демографических процессов в нашей стране сопряжен с целым рядом трудностей. Прежде всего, это вопрос полноты и достоверности статистико-демографических данных.

Проблема полноты и достоверности статистических данных существовала всегда, безотносительно к историческому периоду, политическому режиму, и прежде всего как проблема методологического и методического порядка. Уникальность нашей страны проявляется в том, что на протяжении нескольких десятилетий демографическая статистика рассматривалась как важный идеологический инструмент, способный оказать влияние на сознание масс, в связи с чем ставилась в угоду правящей партии, определялась «вождями», и, в конечном счете, скорее искажала, чем отражала объективное положение вещей. Различного рода статистические приписки имели место на самых различных уровнях: от рядового бухгалтера и счетовода, до таких масштабных акций как Всесоюзные переписи населения.

Переписи населения СССР 1937 и 1939 гг. проводились в сложных социальноэкономических и политических условиях, что в свою очередь неизбежно ставит вопрос о достоверности полученных в ходе их проведения данных. Если с точки зрения статистики материалы Всесоюзной переписи 1937 г. отличала высокая степень достоверности, то власть поставила их под сомнение, и не столько из-за точности полученных данных, сколько именно потому, что перепись раскрыла сложную демографическую ситуацию в стране в результате форсированного строительства «нового общества».

Проведенная через два года – в 1939 г. перепись, предоставила результаты удовлетворившие власть, что было достигнуто за счет приписок и целенаправленной фальсификации данных. Проблема достоверности, таким образом, снова актуализируется при использовании ее материалов для изучения состояния и динамики демографических процессов.

Фальсификации, сокрытие от общественности и научного сообщества статистистико-демографических данных, а так же их нерегулярность и разрозненность в период 1920-1930-х гг. побуждает обратиться при изучении населения к вероятностно-статистическим методам математики, позволяющим моделировать демографические процессы и структуры, определять масштабы демографических потерь и проч.

Одновременно необходимость пользоваться неполными и косвенными данными в последние годы выступает одним из побудительных мотивов развития математической теории. В отечественной и зарубежной науке достаточно широко осуществляются методологические изыскания в области математических методов, которые позволяют получать достоверные результаты по ненадежным и неполным данным [1, с. 13–14].

Демографические модели в виде прогнозов имеют исключительное значение. Как отмечает академик Струмилин С.Г. «Данные переписи … при надлежащем их использовании позволяют нам на десятки лет вперед заглянуть в наше будущее.., т.е. тенденции будущего, которые целиком уже заключены в нашем настоящем, должны быть выявлены во весь их рост» [2, с. 40].

Для целей исторической демографии прогнозы имеют ретроспективное значение и в случае, когда демографические отношения подверглись деформации под влиянием той или иной катастрофы, сравнение данных демографического прогноза с действительностью позволяет определить эффект воздействия этой катастрофы в демографической области [3, с. 12].

Для оценки вероятной численности населения Краснодарского края и потерь, связанных с голодом, репрессиями в 1920-1930-х гг. нами были применены методы регрессионного анализа и аппарат временных рядов для построения вероятностно-статистической модели зависимости общей численности населения региона от исторического года наблюдения. Для построения модели были использованы разрозненные статистические данные, как во временном отношении, так и в административнотерриториальном. Статистико-временной ряд представлен данными о численности населения региона за следующие годы: 1870–1916, 1920, 1923, 1926, 1937 гг. [4], а также данными о численности населения Северо-Кавказского края в 1926, 1928, 1931, 1933, 1934, 1940 гг.

Предварительно исходные данные были пересчитаны в границах Краснодарского края с учетом всех имевших место административно-территориальных изменений.

В регрессионном анализе моделируется взаимосвязь одной случайной переменной от одной или нескольких других случайных переменных. При этом первая переменная называется зависимой, а остальные – независимыми. Выбор или назначение зависимой и независимых переменных является произвольным (условным) и осуществляется исследователем в зависимости от решаемой им задачи. Независимые переменные называются факторами, регрессорами или предикторами, а зависимая переменная – результативным признаком, или откликом.

Если число предикторов равно 1, регрессию называют простой, или однофакторной, если число предикторов больше 1 – множественной или многофакторной. В общем случае регрессионную модель можно записать следующим образом:

y = f(x1, x2, …, xn), где y – зависимая переменная (отклик), xi (i = 1,…, n) – предикторы (факторы), n – число предикторов.

В качестве инструментария вероятностно-статистического моделирования численности населения использовали статистический пакет прикладных программ STATISTICA 6.1 [5]. Регрессионные модели строили по историческим данным общей численности населения Кубанской и Черноморской областей с 1870 по 1916 гг. В качестве предиктора использовали условный год, равный разности реального года и начального года наблюдений – 1870 г.

Линейная регрессия имеет вид:

Численность общая = 197,7237 + 54,4491× Условный год

Значения коэффициента детерминации R2 = 0,968 и коэффициента множественной корреляции R = 0,988, близкие к 1, свидетельствуют о высокой адекватности модели. Уравнение регрессии объясняет 96,8% исходной изменчивости и только 3,4% остаточной изменчивости остаются необъясненными.

Квадратичная регрессия имеет вид:

Численность общая = 320,9727 + 43,3799× Условный год + 0,184× Условный год ²

Значения коэффициента детерминации R2 = 0,966 и коэффициента множественной корреляции R = 0,988, близкие к 1, свидетельствуют о высокой адекватности модели.

Регрессионными моделями были предсказаны значения общей численности населения с 1917 по 1926 гг., при этом были известны данные за 1920, 1923, 1926 гг. Результаты расчетов представлены в табл. 1. Возможные значения численности за 1939 гг., вычисленные по линейной и квадратичной модели, составили соответственно 4 227 и 4 538,4 тыс. чел. Построенные зависимости хорошо моделируют тренд демографических процессов, происходящих на Кубани, свидетельствующий о росте численности населения. Модели дают правдоподобный прогноз на 1939 г., но из-за монотонности не видят тенденцию резкого снижения численности в 1920, 1923, 1926 гг.

Для устранения этого недостатка была построена кубическая регрессионная модель зависимости общей численности населения Кубани от условного года за период времени с 1913 по 1926 гг.: Численность общая = – 377 440 + 21 268× Условный год – 395 × Условный год ² + 2× Условный год ³

Значения коэффициента детерминации R2 = 0,98 и коэффициента множественной корреляции R = 0,99, близкие к 1, свидетельствуют о высокой адекватности модели. Уравнение регрессии объясняет 98% исходной изменчивости и только 2% остаточной изменчивости остаются необъяс-ненными.

Из таблицы видно, что при прогнозировании значений численности населения на период времени с 1917 по 1926 гг. наиболее адекватными являются результаты, полученные кубической регрессией. Но из-за высокой скорости роста кубической функции получить достоверный прогноз на 1939 г. не удалось.

Таблица 1

Прогноз изменения численности населения Краснодарского края на 1920–1930-е гг., тыс. чел.

Год	Условный год	Численность общая	Линейная регрессия	Квадратичная регрессия	Кубическая регрессия
1913	48	3104,2
1914	49	3244,8
1915	50	3281,9
1916	51	3357,8
1917	52		3029,1	3074,1	3286,6
1918	53		3083,5	3136,8	3219,3
1919	54		3138,0	3199,9	3135,6
1920	55	3035,6	3192,4	3263,3	3050,0
1921	56		3246,9	3327,1	2977,2
1922	57		3301,3	3391,3	2931,7
1923	58	2936,3	3355,8	3455,8	2928,0
1924	59		3410,2	3520,7	2980,9
1925	60		3464,7	3586,0	3104,8
1926	61	3312,5	3519,1	3651,6	3314,3
1939	74		4227,0	4538,4

По известным статистическим данным и предсказанным кубической моделью значениям численности населения, был составлен временной ряд и использован мощный математический аппарат временных рядов для построения прогноза общей численности населения Краснодарского края на 1939 г.

Под временным (динамическим) рядом подразумевается последовательность наблюдений некоторого признака Х (случайной величины) в последовательные равноотстоящие моменты t . Отдельные наблюдения называются уровнями ряда и обозначаются х t , t = 1, …, n.

При исследовании временного ряда выделяются несколько составляющих:

• x, = U, + Y, + c, + E, X „

• ^{t t t t t} , t = 1 , …, n,

где ut – тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов (убыль населения, уменьшение доходов и т.д.); γt – сезонная компонента, отражающая повторяемость процессов в течение не очень длительного периода (дня, недели, месяца и т.д.); сt – циклическая компонента, отражающая повторяемость процессов в течение длительных периодов време- ни свыше одного года; εt – случайная компонента, отражающая влияние не поддающихся учету и регистрации случайных факторов.

Для выявления периода цикличности в анализируемых данных использовали спектральный анализ, которым были выявлены циклы различной периодичности: в 18, 56, 14, 28, 11, 9, 7 и т.д. лет.

Моделирование временного ряда проводили при установках диалога Одномерная АРПСС : р – авторегрессии = 1; q – скользящих средних = 0; P – сезонных = 0; Q – сезонных = 0. Результаты прогнозирования методом АРПСС общей численности населения с 1927 по 1939 гг. представлены на рис.1.

Прогнозируемое значение численности населения на 1939 г. составляет примерно 4 044 тыс. чел. при 95%-м доверительном интервале [2404,7; 6800,7]. Это означает, что с вероятностью 0,95 истинное значение численности населения в 1939 г. находится в указанном интервале. Из графика видно, что с увеличением даты прогноза доверительный интервал возрастает, т.е. чем отдаленнее точка прогноза, тем менее достоверным является его результат. Достоинством модели является то, что тренд предсказанных значений численности населения с 1927 г. в целом верно моделирует тренд исходных значений с 1870 по 1926 г., предсказанная на 1939 г. численность населения, которая составляет примерно 4 млн. чел., обладает исторической правдоподобностью. Недостатком является достаточно широкий доверительный интервал.

Прогнозы; Модель:(1,1,0)(0,1,0) Сезонный лаг: 12

Исход.:Общая численность

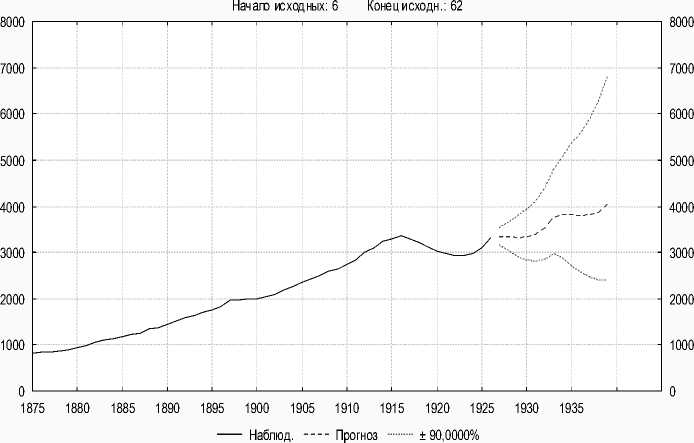
Рис.1. Прогноз изменения численности населения Краснодарского края на 1930–1940-е гг.

Простая и прагматически ясная модель временного ряда имеет следующий вид:

Xt = β + Εt, где β – константа; Εt – случайная ошибка. Константа β относительно стабильна на каждом временном интервале, но может также медленно изменяться со временем. Один из интуитивно ясных способов выделения β состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются больший вес, чем предпоследним, предпоследним – еще больший вес, чем предпредпоследним и т.д. Простое экспоненциальное сглаживание именно так и устроено. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет вид:

S t = α X t + (1 – α ) S t – 1 .

Когда эта формула применяется рекурсивно, каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Эмпирические исследования показали, что весьма часто простое экспоненциальное сглаживание дает достаточно точный прогноз.

Очевидно, результат сглаживания зависит от параметра а (альфа). Если а равно 1, то предыдущие наблюдения полностью игнорируются. Если а равно 0, то игнорируются текущие наблюдения. Значения а между 0 и 1 дают промежуточные результаты.

Экспериментально по критериям качества модели удалось подобрать параметры модели экспоненциального сглаживания. Метод экспоненциального сглаживания реализовали посредством процедуры Автоматического поиска оптимальных параметров модели, которые приняли следующие значения: α (альфа) = 0,83; δ (дельта) = 0; γ (гамма) = 0. Прогноз на 1939 г. составил 3 952,539, что несколько меньше чем прогноз, сделанный методом АРПСС (4 043,977).

Посредством среднего процента годового прироста населения Северо-Кавказского края была оценена общая численность населения Краснодарского края на 1939 г., в состав которого вошли Кубанский, Майкопский, Армавирский, Черноморский округа и отдельные территории, ранее находившиеся в составе Северо-Кавказского края. Оценка достаточно грубая, так как основана на не вполне очевидных предположениях.

Предположение 1. Средний процент прироста населения Северо-Кавказского края является устойчивой и информативной характеристикой изменения численности населения края в период с 1926 по 1939 гг.

Предположение 2. Общая численность населения Краснодарского края изменялась в рассматриваемом периоде времени такими же темпами, как и население Северо-Кавказского края, т.е. имела такой же средний процент прироста.

Средний процент годового прироста населения Северо-Кавказского края определили посредством анализа динамики численности населения края с 1926 по 1940 гг., которая представлена в табл. 2.

Таблица 2

Динамика численности населения Северо-Кавказского края в 1926-1940 гг., тыс. чел.

Год	Численность населения	Процент изменения
1926	8364,1
1928	8624,0	3%
1931	8123,7	- 6 %
1933	9878,7	22%
1934	9587,7	- 3%
1940	10494,0	9%
Сумма набл.		25%

В третьем столбце таблицы приведен процент изменения численности населения края, относительно численности за предыдущий период времени. Например,

3% = ((8 624 – 83 664,1)/8364,1)×100%.

По таблице легко посчитать, что суммарный прирост населения по данным численности за 1926, 1928, 1931, 1933, 1934, 1940 гг. составит примерно 25%. Тогда средний процент годового прироста населения с 1926 по 1940 гг. будет равен

25% / 14 = 1,7857%.

Тогда, предсказанное значение численности населения можно посчитать по формуле сложных процентов:

Vk = V0 х (1 + 0,017857)k где V0 – значение численности населения в начальный период времени (в нашем случае 1926 г.), k номер года на который строится прогноз, считая, что 1926 г. имеет нулевой номер. Например, 1939 г. имеет номер 13, соответственно 1940 г. имеет номер 14.

Если V 0 = 3 312,5, что соответствует общей численности населения Краснодарского края (в границах Кубанской области и Черноморской губернии) в 1926 г., то

V14 = 3 312,5 × 1,01785714 = 3 312,5 × 1,1116 = 3 683 тыс. чел., где V14 – это общая численность населения Краснодарского края в 1940 г.

Аналогично можно посчитать V 13 = 3 619 тыс. чел. – предсказанную общую численность населения Краснодарского края в 1939 г.

Таким образом, посредством различных математических методов при различных уровнях достоверности и степени приближения, нами получено пять предсказанных значений общей чис- ленности населения Краснодарского края на 1939 г.: 4 227,0; 4 538,4; 4 044,0; 3 952,5; 3 619 тыс. чел. Не будет ошибкой, если в качестве предполагаемого значения численности населения в 1939 г. воспользуемся средней арифметической по этим пяти вычисленным значениям, которое равно (4 227,0 + 4 538,4 + 4 044,0 + 3 952,5 + 3 619,0) / 5 = 4 082,18 тыс. чел.

Следовательно, справедливым будет утверждение, что общая численность населения Краснодарского края к 1939 г. при сложившихся темпах прироста и в условиях отсутствия катастроф должна была составить величину не менее 4 млн чел.

Фактическая численность населения Краснодарского края, показанная переписью 1939 г., составила 3 172 674 чел. (с Адыгейской АО) и 2 930 875 чел. (без Адыгейской АО) [6], исключая приписки 3 102 757 (с Адыгейской АО) и 2 865 046 чел. (без Адыгейской АО) [7, с. 91].

Такой значительный разрыв между предполагаемой и фактической численностью населения в Краснодарском крае позволяет говорить о значительных масштабах прямых и косвенных потерь населения региона вследствие голода начала 1920-х гг. и 1932-1933 гг., индустриализации и коллективизации, раскулачивания, принудительного переселения сотен тысяч кубанских семей за пределы края, репрессиями и депортациями представителей отдельных народов с территории края.