Оценка динамических потерь в силовых ключах автономных инверторов при различных алгоритмах модуляции

Регулирование скорости асинхронного двигателя (АД) в частотно-регулируемых асинхронных электроприводах (ЭП) осуществляется с использованием различных схем преобразователей частоты (ПЧ) ( Асанов и др., 2002; Сидоров, 2009; Hota et al., 2017 ) и алгоритмов управления его силовыми ключами ( Васильев и др., 2014; 2020; Andreev et al., 2018 ). При этом для значительного класса ЭП актуальна проблема энергосбережения ( Andreev et al. , 2017; Vodovozov et al., 2019 ). Основной фактор, влияющий на выбор того или иного алгоритма управления с целью уменьшения энергопотребления, – величина динамических потерь в силовых полупроводниковых ключах ПЧ.

Целью настоящего исследования является определение алгоритма модуляции, обеспечивающего минимизацию динамических потерь в силовых полупроводниковых ключах ПЧ при скалярных алгоритмах управления.

Материалы и методы

В процессе исследования применялся метод математического моделирования системы АИН – АД (автономный инвертор напряжения – асинхронный двигатель) в высокоскоростных ЭП с целью оценки величины потерь энергии при коммутации силовых полупроводниковых ключей ПЧ (динамических потерь). Для решения поставленных задач использовалось представление АД в виде системы нелинейных дифференциальных уравнений. Коэффициенты в дифференциальных уравнениях, входящих в данную систему, определялись параметрами асинхронного двигателя 4А225М2У3, выбранного в качестве объекта исследования, совместно с силовыми полупроводниковыми ключами IGBT IXGK120N120B3. Оценка величины динамических потерь проводилась для скалярных (модульных) алгоритмов управления асинхронного электропривода.

Приближенно энергию потерь на включение и выключение ключа можно определить исходя из стилизованной формы импульса прямого тока, изображенной на рис. 1 ( Воронин, 2005 ), где представлены следующие обозначения: I _м – амплитуда прямого тока, протекающего через ключ; t _P = t ₃ – t ₂ – длительность прямого тока; t _R = t ₂ – t ₁ – время нарастания прямого тока (время включения); t _F = t ₄ – t ₃ – время спада прямого тока (время выключения).

Энергия потерь на включение, Дж, полностью управляемого силового полупроводникового ключа вычисляется по формуле t2

e _on = J i ( t MtW,                                     (1)

ti где i(t) – мгновенное значение тока; u(t) – мгновенное значение напряжения.

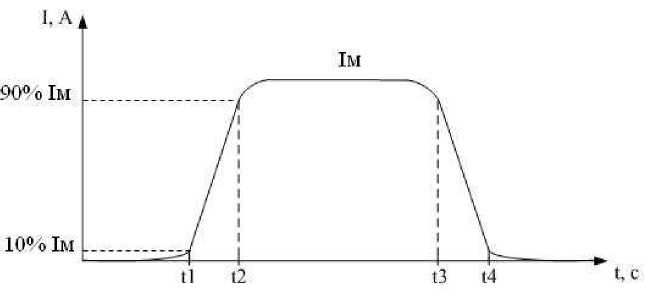
Рис. 1. Стилизованная форма импульса прямого тока

Fig. 1. Stylized forward current impulse shape

Энергия потерь на выключение, Дж, полностью управляемого силового полупроводникового ключа определяется так:

t 4

E OFF = J i ( t ) u ( t ) dt .                                                 (2)

t ₃

В асинхронном частотно-регулируемом ЭП в фазах нагрузки обеспечивается режим непрерывного тока, поэтому для упрощения нахождения интегралов (1) и (2) используются типовые кривые тока и напряжения при включении и выключении ключа (рис. 2) ( Воронин, 2005 ).

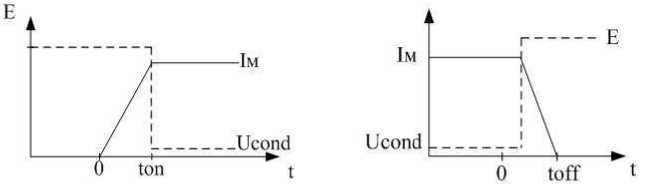
а

б

Рис. 2. Типовые кривые переходного процесса в режиме непрерывных токов: а – включения; б – выключения Fig. 2. Typical curves of the transient process in continuous current mode: a – switching on; б – switching off

В этом случае потери энергии при включении вычисляются по следующей формуле:

,7    _ ¹M ^EtR

Eon =   2 ’ где E – напряжение, прикладываемое к закрытому ключу, В.

Потери энергии на выключение будут определяться как

I _M Et _F

^E OFF ⁼  ₂

.

Мощность динамических потерь на периоде формируемого напряжения для одной фазы находится таким образом:

1 ^N

P df = ~ ^ ( E ON + E OFF ),

T s i = 1

где T s – период формируемого напряжения, с; ^ – количество интервалов модуляции на периоде формируемого напряжения.

Результаты и обсуждение

При определении величины динамических потерь необходимо учитывать величины фронтов включения и выключения; мгновенные значения тока, протекающего через ключ в течение периода модуляции, и напряжения, под действие которого попадает ключ в закрытом состоянии. Для упрощения анализа примем допущение о неизменности значения тока, протекающего через полупроводниковый ключ на периоде модуляции. Оценку величины динамических потерь выполним для квазиустановившегося режима работы ЭП с номинальным моментом сопротивления на валу АД с использованием классической схемы трехфазного автономного инвертора напряжения (АИН) (рис. 3), которая также называется схемой одноуровневого АИН ( Асанов и др. , 2002 ; Машкин и др., 2018 ).

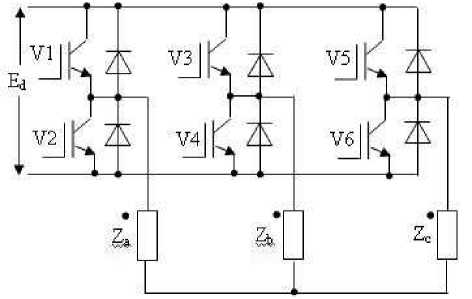
Рис. 3. Схема классического трехфазного АИН

Fig. 3. Scheme of a classic three-phase AVI

При помощи данной схемы ПЧ возможна реализация как векторных ( Александров и др., 2019; Виноградов, 2008; Плотников и др., 2016 ), так и скалярных (модульных) алгоритмов управления ( Шонин и др., 2016; Habbi et al., 2016; Zhang et al., 2019 ). При реализации векторных и скалярных алгоритмов управления обычно формируются синусоидальные огибающие напряжений на фазах АД или кривые, в спектре которых допускается присутствие высших гармонических составляющих с незначительной амплитудой. Например, в случае использования скалярных алгоритмов управления могут использоваться такие виды модуляции, как двухполярная сплошная синусоидальная модуляция (ДССМ), двухполярная синусоидальная модуляция (ДСМ) на крайних интервалах, симплексная синусоидальная модуляция (ССМ), симплексная линейная модуляция (СЛМ) ( Грузов и др. , 2000; 2001 ).

В высокоскоростных электроприводах и ЭП, где не требуется значительное регулирование скорости вниз, могут использоваться алгоритмы широтно-импульсного регулирования (ШИР), например, двухполярная прямоугольная модуляция (двухполярное ШИР) и однополярная прямоугольная модуляция (однополярное ШИР) ( Программа расчета спектрального состава…, 2019 ). Диаграмма управляющих импульсов двухполярной прямоугольной модуляции представлена на рис. 4, однополярной прямоугольной модуляции – на рис. 5 ( Mashkin et al., 2020 ).

Рис. 4. Диаграмма управляющих импульсов при двухполярном ШИР

Fig. 4. Control pulse diagram for bipolar PWM

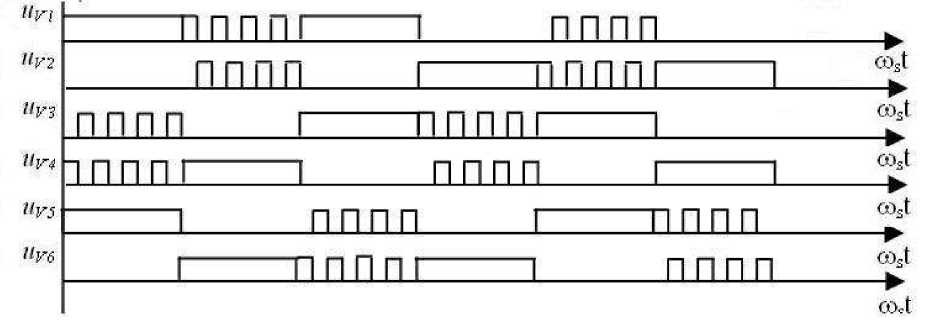
Рис. 5. Диаграмма управляющих импульсов при однополярном ШИР

Fig. 5. Control pulse diagram for unipolar PWM

Алгоритмы ШИР используются для управления ЭП, обеспечивающими приведение в движение механизмов, имеющих вентиляторную характеристику. Упрощенно (при пренебрежении трением) вентиляторная характеристика механизма описывается следующим уравнением:

I to I M с (to) = М н |     I ,

V ^to H )

где M _н – номинальный момент двигателя, Н·м; ω _н – номинальная скорость вращения вала двигателя.

Для оценки динамических потерь в ключах АИН при установившимся режиме работы можно воспользоваться Т-образной схемой замещения фазы АД. Формируемую кривую ступенчатого напряжения на фазе статора АД раскладывают в ряд Фурье, по известным параметрам схемы замещения получают амплитуды гармонических составляющих тока, а также фазовые сдвиги между гармониками токов и напряжений ( Машкин и др., 2018 ), и далее, просуммировав динамические потери в силовых ключах от каждой гармоники тока, находят общие динамические потери. Однако в этом случае более целесообразно решить нелинейную систему дифференциальных уравнений, представляющих математическую модель АД ( Mashkin at al., 2020 ):

^U sa

^U sb

U sc

= rsis+Ldisa + Ldira, s sa s dt µ dt disb       dirb

• i + -L             + L.            , s sb    s dt     µ dt

= r_si_{s c}+ Ldi sc + Ldi rc , s sc    s _dt      µ _dt

. 0 = rrira + L di + L^ di  - -L (L (irb - irc) + L^ (isb - i)) mp, dt dt V3

di„>.         di„>.1

0 = rr irb + Lr -"TT + L^ -"L Tr( Lr (irc - ira ) + LV (isc - isa )) ®Pn , dt      dtV3

dirc       disc1

0 = rr irc + Lr —7~ + L^    ---/= (Lr (ira - irb ) + L^ (isa - isb )) ®pn , dt      dtV3

.dm

M - Мг = J— c dt где isa, isb, isc – токи фаз a, b, c статора асинхронного двигателя, А; ira, irb, irc – токи эквивалентных фаз a, b, c ротора, А; ω – скорость вращения ротора, рад/c; Lµ, Ls, Lr – индуктивности намагничивающего контура, полного контура статора, полного контура ротора, Гн; Usa, Usb, Usc – напряжения, подаваемые на статор асинхронного двигателя, В.

Для решения системы нелинейных дифференциальных уравнений с учетом специфики моделируемого объекта управления (ЭП) можно воспользоваться алгоритмом, приведенным в работе ( Mashkin et al., 2019 ).

В качестве нагрузки, на которую работает ПЧ, выберем АД 4А225M2УЗ с номинальной мощностью P _н = 55 кВт, основные параметры которого ( Кравчик и др., 1982 ) приведены в табл. 1. Параметры его Т-образной схемы замещения указаны в табл. 2, где использованы обозначения: r _s – активное сопротивление фазы статора; r _r – активное сопротивление фазы ротора; x _µ – индуктивное сопротивление намагничивающего контура; x _s – индуктивное сопротивление фазы статора; x _r – индуктивное сопротивление фазы ротора.

Таблица 1. Параметры АД 4А225М2У3 Table 1. AM 4А225М2У3 parameters

Р н , кВт	М н , Н·м	I sн , А	КПД, %	cos φ
55	178,28	99,54	91	0,92

Таблица 2. Параметры Т-образной схемы замещения АД 4А225М2У3 Table 2. Parameters of the T-shaped equivalent circuit AM 4A225M2У3

r s , Ом	r r , Ом	x µ , Ом	x s , Ом	x r , Ом
0,057	0,041	12,38	12,58	12,63

Для проведения оценки динамических потерь при выбранных алгоритмах прямоугольной модуляции используем в качестве силовых полупроводниковых ключей IGBT IXGK120N120B3, основные параметры которого приведены в табл. 3, где указаны следующие обозначения: U кэ – предельно допустимое напряжение коллектор-эмиттер; U нас. кэ – напряжение насыщения коллектор-эмиттер; I к – максимальный постоянный ток коллектора; t вкл – время включения; t выкл – время выключения.

Таблица 3. Основные параметры IGBT IXGK120N120B3 Table 3. Basic parameters of IGBT IXGK120N120B3

U кэ , В	U нас. кэ ,В	I к , А	t вкл , нс	t выкл , нс
1 200	3	200	124	420

При работе АД, обеспечивающего приведение в движение механизма, обладающего вентиляторной механической характеристикой, момент сопротивления на валу двигателя будет падать вместе со снижением скорости; в этом случае достаточно выбрать простейший алгоритм скалярного управления – пропорциональное управление, при котором обеспечивается выполнение условия

U / f = const, ss где Us – действующие значение напряжения статора, В; fs – частота формируемого на статоре напряжения, Гц.

Механическая характеристика асинхронного двигателя в общем виде при скалярных (модульных) законах управления в частотно-регулируемом ЭП определяется следующим уравнением ( Mashkin et al., 2018 ):

* 2          2U2

м = ms Р п I ux I rr    xVU SH

M          I * I * 2?      * ,

^2nf S H \ f s J ^f _r F ( f s , f r )

где m _s – число фаз обмотки статора;

F ( f . , f r ) =

r s r r

, 2 /

'l I f.‘ fr*

- x * x . ^

+

r       r

-5* x s + -x x r

V f r        f s

;

a = 1 -

µ

x _s x _x

коэффициент рассеяния машины; f * = -f s относительная частота тока статора; / * = sf / - относительная s    f s _H

*

частота тока ротора; u _s

U s

U S H

– относительное напряжение фазы статора АД; p _п – число пар полюсов АД;

f sн – номинальная частота напряжения, подводимого к фазе статора АД, Гц; U sн – действующее значение номинального напряжения, подводимое к фазе статора АД.

Отношение u _s ^* / f _s ^* в формуле (3) определяет используемый закон скалярного управления. Для пропорционального закона управления это отношение численно равно единице. На рис. 6 приведены механические характеристики асинхронного двигателя 4А225М2У3 при пропорциональном законе управления и частотах формируемого на статоре напряжения f _s = 50; 37,5; 25; 12,5 Гц, а также механическая характеристика механизма, имеющего вентиляторную характеристику.

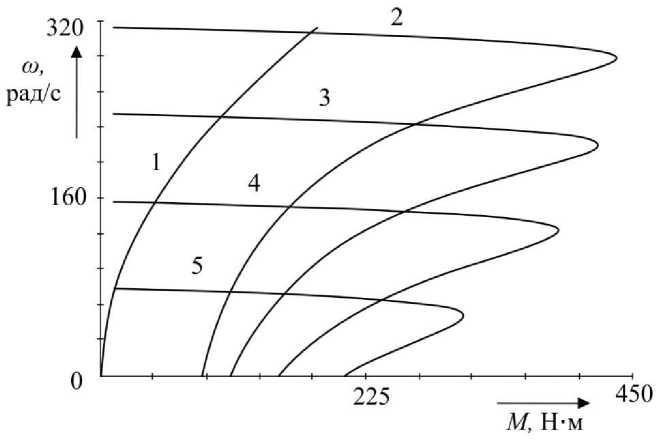
Рис. 6. Механические характеристики нагрузки (1) и АД 4А225М2У3 при f s = 50 Гц (2), f s = 37,5 Гц (3), f s = 25 Гц (4), f s = 12,5 Гц (5)

Fig. 6. Mechanical characteristics of load (1) and AD 4A225M2U3 at f _s = 50 Hz (2), f s = 37.5 Hz (3), f s = 25 Hz (4), f s = 12.5 Hz (5)

Оценка динамических потерь для одной фазы при различных частотах модуляции на рабочих точках механической характеристики отражена в табл. 4.

Таблица 4. Динамические потери в ключах АИН при работе на АД 4А225М2У3 Table 4. Dynamic losses in the AVI keys when operating on AM 4A225M2У3

f s , Гц	M , Н·м c ,	f м , Гц	P дин , Вт
			Двухполярное ШИР	Однополярное ШИР
50	178	6 000	140,2	60,4
		500	7,3	1,2
37,5	100	6 000	83,2	32,8
		500	4,2	1,2
25	45	6 000	51,2	17,6
		500	5,7	2,1
12,5	11	6 000	42,1	12,8
		500	9,3	2,1

Заключение

На основе проведенного моделирования можно сделать следующие выводы:

• 1)    при типичной частоте модуляции f м = 6000 Гц и применении скалярных алгоритмов управления обеспечивается достаточная степень аппроксимации формируемых огибающих фазных напряжений к синусоидальной форме, при использовании алгоритмов ШИР наблюдаются значительные динамические потери в ключах АИН;

• 2)    в ходе применения алгоритмов ШИР не требуется точной аппроксимации синусоидальной формы, в результате чего появляется возможность сокращения частоты модуляции и, как следствие, уменьшения величины динамических потерь в ключах АИН;

• 3)    алгоритм однополярной прямоугольной модуляции (однополярное ШИР) при любых режимах нагрузки и значениях частоты модуляции обеспечивает меньшие динамические потери в ключах АИН по сравнению с алгоритмом двухполярной прямоугольной модуляции (двухполярное ШИР).