Оценка достоверности идентификации АТС по методу многомерного анализа с использованием теории статистических решений Неймана-Пирсона

Сигнал, регистрируемый оптикоэлектронным датчиком, является оптическим образом автотранспортного средства (АТС) [1,2]. Оптическое поле меняется при движении АТС. Автомобиль перекрывает кузовом часть оптического фона, обусловленного излучением Солнца, атмосферы, осветительных фонарей. Оптический образ в этом случае определяется формой и размером автомобиля и полем зрения приемника, а также тепловым излучением двигателя и контрастом. Отдельные части поверхности автомобиля отражают излучение различных источников, изменяя тем самым оптическое поле. Образ зависит от отражательной способности материала автомобиля, а также от ориентации отражающих поверхностей автомобиля по отношению к источнику излучения [3].

Метод произведений является частным случаем многомерного анализа.

Предположим, имеется многомерное пространство признаков (пространство критериев), каждый из которых входит в уравнение вида:

y = Ax a 1 • x a 2 ...• x a k . (1).

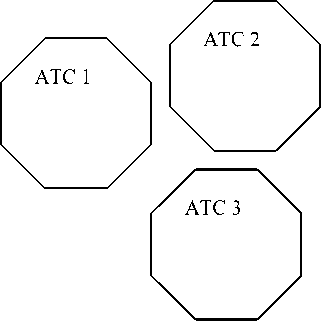
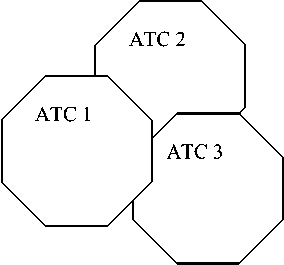
В пространстве признаков каждое транспортное средство занимает некоторый объём. Для класса данный объём имеет нечёткие границы. В случае выполнения условия не пересечения объёмов (рис. 1,а) разделение АТС по классам по величине определяющих произведений не представляет сложности. Если объёмы частично пересекаются (рис. 1,б), что эквивалентно математической операции -“И”, то задача разделения на классы усложняется. В этом случае требуется рассчитать вероятность правильного обнаружения и ложной тревоги. Количество критериев в определяющем произведении, а

Оценка достоверности идентификации АТС по методу многомерного анализа с использованием теории статистических решений Неймана-Пирсона тем самым и сложность применяемого алгоритма выбирается из допустимых вероятностей и цены ошибки. Оптимальное число критериев определяется числом 7. В работе [4] приведены результаты разделения АТС по классам в одномерном, двумерном и трёхмерном пространстве признаков рассчитаны значения определяющих произведений по классам АТС. Функции плотности вероятности значений определяющих произведений по классам представлены на рис. 2.

В качестве примера ниже приведён один из возможных алгоритмов распознавания образов транспортных средств по методу произведений. Оптический образ получен при прохождении в поле зрения растра троллейбуса “ЗИУ-9Б”. В качестве взаимно независимых показателей (основных влияющих факторов) выбрано произведение амплитудного максимума i (максимальная интенсивность сигнала) и максимального значения по оси абцисс t (время существования сигнала), а также прямое и обратное отношение t к i .

а)                                                           б)

Рисунок 1 . Схематичное представление “объёмов”, занимаемых классами АТС в многомерном пространстве признаков

Анализ характера задачи распознавания в условиях, проиллюстрированных на рис. 1 б, т.е. при наличии вероятностной связи между признаками объектов и классами АТС, показал, что для построения алгоритмов распознавания с успехом может быть использована теория статистических решений, или теория проверки гипотез, созданная Ю. Нейманом и Э. Пирсоном [5]. Если объект относится к классу I, а его считают объектом класса II, то совершена ошибка, которая называется ошибкой первого рода [6]. По терминологии теории статистических решений, ошибочно выбрана гипотеза H2, в то время как справедлива гипотеза H1. Вероятность ошибки первого рода, т.е. вероятность от- нести объект к классу II, когда он относится к классу I:

∞

Q 1 = ∫ f 1 ( X ) dX .               (2)

X 0

Наоборот, если справедлива гипотеза H 2 , а отдано предпочтение гипотезе H 1 , то совершена ошибка второго рода, вероятность которой

X 0

Q 2 = ∫ f 2 ( X ) dX .            (3)

-∞

Q 2 есть вероятность выбрать гипотезу H 1 , когда справедлива гипотеза H 2 .

В некоторых приложениях теории статистических решений вероятность ошибки первого рода подчас называют вероятностью ложной тревоги, в то время как вероятность ошибки второго рода – вероятностью пропуска цели.

О.В. Маковецкая-Абрамова, М.Ф. Кунин

Поиск границ между классами АТС осуществлен при помощи программы Quest. Вероятность неверного заключения при распознавании транспортных средств двух соседних классов (легковых и малотоннажных автобусов) составила:

• -    по одному независимому критерию (времени существования сигнала) – 70 %;

• -    по двум независимым критериям (произведению амплитудного максимума сигнала и времени существования сигнала) – 18 %;

• -    по трём  независимым критериям

(произведению  квадрата амплитудного максимума и времени существования сигнала, что в физическом смысле близко энергии сигнала) – 0 %.

Таким образом, можно сделать заключение о том, что метод произведений с вероятностной точностью 100 % позволяет разделить транспортные средства по классам и идентифицировать их.

Графическое представление результатов поиска границ и гистограммы частот объектов представлены на рис. 2.

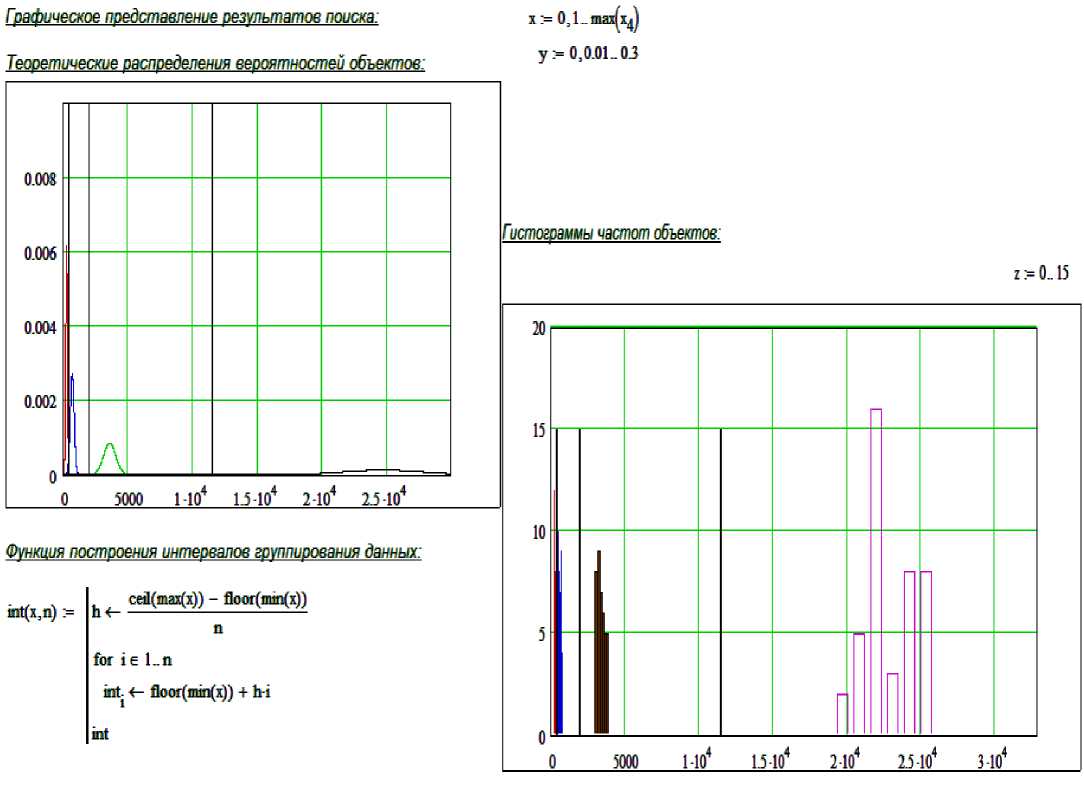
Рисунок 2. Результаты поиска границ классов АТС

Оценка достоверности идентификации АТС по методу многомерного анализа с использованием теории статистических решений Неймана-Пирсона Программа распознавания образов транспортных средств по методу произведений

ORIGIN з= 1 Принимаем минимальный индекс массива равным 1

Перевод сигнала в область положительных чисел tnins з= min(s)

i з= 1.. lens

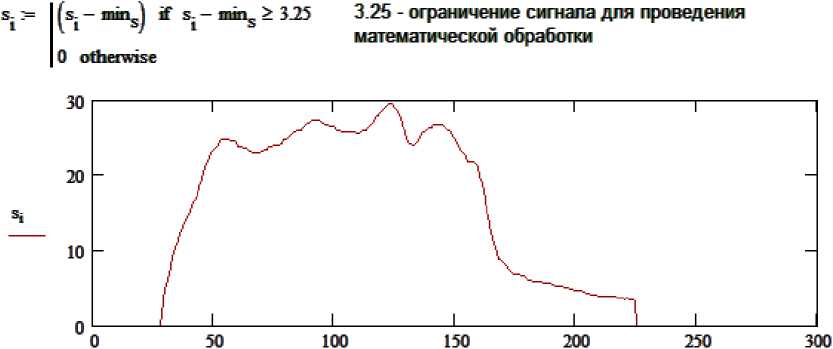
Классификация транспортного средства по методу произведений heights := max(s) heights = 29.6 Определение максимальной интенсивности сигнала indexes з= 28                        Начало сигнала indexes., з= 225                        Конец сигнала len_s з= indexes2 - indexes 1   len_s = 197 Определение времени существования сигнала heights " len-s = 58312 Произведение i х t kn-s _ 6 655           Отношение t / i heights heightg

------= 0.15             Отношение i /1 len s

• ¹    Маковецкая-Абрамова Ольга Валентиновна – кандидат технических наук, доцент кафедры «Технология обслуживания транспортных средств» Санкт-Петербургского государственного университета сервиса и экономики, тел.+79215569306,e-mail: abramova19701970@mail.ru;

• ²    Кунин Михаил Фёдорович – инженер кафедры «Автомобильный транспорт» Владимирского государственного университета, тел.+79101857280,e-mail: mihail.kunin@mail.ru