Оценка формы цепных углеводородных молекул методом Монте-Карло

Углеводородные цепные молекулы (молекулы, состоящие из групп CHn (n = 1, 2, 3), валентно связанных в цепь) являются объектами исследования многих областей науки: физики конденсированного состояния, физики высокомолекулярных соединений (полимеров), молекулярной физики, биофизики и т. д. Кроме того, такие молекулы широко применяются в производстве, например, поверхностно-активных веществ [6], синтетических волокон [22], [26], [35], эластомеров [23], [24], [32], лакокрасочных материалов, изделий [4]. Углеводородные цепи остатков жирных кислот входят в состав молекул фосфолипидов [2], [12], [25], которые в природе образуют бислойные и другие структурные образования (мембраны, мицеллы и т. п.). Таким образом, изучение физических и химических свойств углеводородных цепных молекул имеет большое значение как для развития многих технологических областей, так и для углубления понимания свойств различных биологических систем.

Важную роль в теоретических интерпретациях поведения и свойств цепных молекул в разно

образных молекулярных системах играет учет их формы [1], [19], [28], [29], [31] (последняя была изучена впервые в работе [21], было показано, что форма усредненной по конформациям полимерной цепи не является сферической). Учет формы важен, например, при описании вязкого потока [33] молекул, при адсорбции на поверхностях, при абсорбции и диффузии в пористых системах [30], [34]. Информация о форме отдельных углеводородных цепей липидов позволяет оценивать степень их совместимости, комплементарности при сосуществовании в бислое при разных условиях [8], [10], [11]. Для исследования формы молекул удобно применять методы компьютерного моделирования: метод молекулярной динамики (МД), метод Монте-Карло (МК), поскольку они позволяют извлечь любую детальную информацию об исследуемых системах.

Жирнокислотные цепи в липидах биомембран могут различаться по химическому строению [2], [12], [25] (мембраны, как правило, гетеро-генны, в них сосуществуют десятки липидных молекул разной структуры). В настоящей работе рассмотрены лишь неразветвленные углеводо- родные цепные молекулы. Это могут быть цепи без двойных связей (насыщенные цепи), а также таковые с двойными связями (ненасыщенные цепи). Методом МК моделировали конформационное поведение молекул общего строения CH3 – (CH2)a – (CH = CH – CH2)d – (CH2)b – CH3 (где a, b, d – целые) при температурах T = 293, 303, 313 K. Прототипами указанных молекул являлись остатки жирных кислот молекул фосфолипидов, в которых проведена замена концевой группы COO на группу CH3. Исследованы цепи с количеством атомов углерода в остове N = 16, 18, 20, 22, количеством двойных связей d = 0, 1, ..., 6 (все – в конфигурации cis). Моделируемые молекулы отличались также положением двойных связей вдоль по цепи. Всего исследовано 65 различных молекул, изучены характеристики их формы.

МОДЕЛЬ

Для сравнения формы углеводородных цепных молекул разного химического строения сле- довало избрать некоторое однотипное состояние молекул и провести расчет свойств единым методом в идентичных условиях. В качестве такового избрано невозмущенное состояние (Θ-условия) [9]. Средние характеристики молекул в Θ-условиях приблизительно соответствуют таковым в жидком или аморфном состояниях вещества [9], [13], [36]. В соответствии с определением невозмущенного состояния [9] моделировали одиночную цепь, в которой учитывали взаимодействия только тех ее атомов, которые находились в пределах некоторых фрагментов вдоль по цепи (то есть ближние взаимодействия). Равновесные свойства такой одиночной цепи вычисляли в рамках так называемой классической гибкой модели [18], согласно которой цепная молекула – это система взаимодействующих материальных точек (разработано несколько типов «гибких моделей» [14], [16], [18]). Для расчета среднего значения какой-либо характеристики H цепной молекулы в NVT-ансамбле использовали выражение

2 л 2 л 2 л

< H > =

J J ... J H (^ 2 ,..., ^ J • exp[ - U_shon (^,^,...,^ - 1 )/ к в Т ] d ф 1 d ^ 2 ... йф^ 1 00  0

2 л 2 л 2 л

J J ... J e^{Xp[ — U}short ⁽ ^ 1 ’ ^Г 2 ’-", ^ N - 1 ) / ^kB^{T ] d} ^ 1 d ^^-" ^d ^ N - 1 00  0

где N – количество атомов углерода в остове цепи; φ ₁, φ ₂, …, φ _N-1 – углы внутреннего вращения (торсионные углы) вокруг C–C связей основной цепи; H ( φ ₁, φ ₂, …, φ _N-1) – заданная характеристика и U_short ( φ ₁, φ ₂, …, φ _N-1) – энергия ближних взаимодействий цепной молекулы в конформации с торсионными углами φ ₁, φ ₂, …, φ _N-1; валентные углы и валентные связи предполагаются зафиксированными вблизи их равновесных значений; k _B – постоянная Больцмана, T – температура. В использованной модели цепи углы внутреннего вращения могли принимать любые значения из диапазона 0–360°.

В данной работе учитывали влияние взаимозависимости изменения каждых трех последовательных торсионных углов молекулы на ее конформационные свойства. Для этого разбивали молекулы на фрагменты, в рамках которых вычисляли ближние взаимодействия. Это осуществляли таким образом, что каждый γ -й фрагмент (при отсчете вдоль по цепи начиная от одного из ее концов) содержал три соседних угла внутреннего вращения φ_γ , φ_{γ +1}, φ_{γ +2}. Смежные фрагменты γ -й и ( γ +1)-й при этом имели два общих торсионных угла – φ_{γ +1}, φ_{γ +2}. Для конструирования любой из рассмотренных молекул по этим правилам

) = _____________exP[— Ushort (Ф\,Ф^:,Фу—-\)1 kBT]_____________ r N-1/      2л2л 2л

Р ( ^ 1 ’ ^ 2

требуется несколько фрагментов из 16 различных типов, которые указаны ниже:

CH3 – CH2 – CH2 – CH2CH2, CH3CH2 – CH2 – CH2 – CH2CH2, CH2CH2 – CH2 – CH2 – CH2CH2, CH2CH2 – CH2 – CH2 – CH2CH, CH2CH2 – CH2 – CH2 – CHCHCH2, CH2CH2 – CH2 – CHCH – CH2CH2, CH3CH2 – CH2 – CH2 – CH2CH, CH2CH2 – CH2 – CHCH – CH2CH, CH2CH2 – CHCH – CH2 – CHCHCH2, CH3 – CH2 – CHCH – CH2CH, CH3CH2 – CHCH – CH2 – CHCHCH2, CH2CHCH – CH2 – CHCH – CH2CH, CH2CHCH – CH2 – CH2 – CH2CH3, CHCH2 – CH2 – CH2 – CH3, CHCH2 – CHCH – CH2 – CH2CH3, CH2CHCH – CH2 – CH2 – CH3.

Символом «–» здесь отмечены валентные связи во фрагменте, взаимозависимость вращений вокруг которых учитывали при моделировании. Вычисление заданной величины < H > из (1) проводили методом МК (метод описан, например, в [17]), то есть определяли ее оценку H . Для этого использовали ранее разработанный алгоритм МК [7] генерирования случайных точек ( ф\ ,ф\,..., ф ^ _— 1 ) в пространстве торсионных углов с плотностью вероятностей

В данном алгоритме конфигурационное пространство трех торсионных углов каждого из фрагментов, из которых состоит рассматриваемая цепь, разбивают на 1 000 000 состояний («параллелепипедов») так, что вероятности их реализации одинаковы, а затем генерируют конформации этой цепи с помощью полученных разбиений. Оценку H величины при использовании этого алгоритма МК следует вычислять согласно выражению [7]

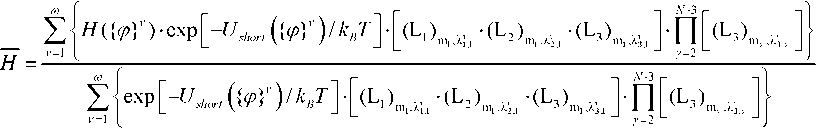
. (3)

Здесь ν – номер текущей конформации; ω – объем выборки конформаций; { ф } ² - координаты случайной точки в пространстве торсионных углов, выбираемой с плотностью вероятностей p ( φ ₁, φ ₂, …, φ _N-1) из выражения (2); величины (Ll).»,^ , (Ч^ ’ ^(L 3 ) m _r , % ², " длины стоРон в угловых единица^, х, того параллелепипеда, который был выбран случайно в процедуре МК в конформации номер ν во фрагменте номер γ типа m . Для вычисления энергии ближних взаимодействий исследуемых молекул использовали силовое поле CHARMM27 [15] с поправками [20]. Для большинства исследованных цепных молекул при вычислении оценок средних характеристик (по формуле (3)) с заданной точностью были использованы выборки в 129 600 000 000 конформаций. В случае пентаеновых и гексаеновых цепей выборки были увеличены в 10 раз, поскольку поверхности потенциальной энергии почти всех их фрагментов характеризуются наиболее пологими минимумами [8].

Для оценки формы молекул в литературе используется несколько подходов (см., например, [19]). В настоящей работе использовали метод аппроксимации формы параллелепипедом. Для этого в каждой конформации данной цепи находили систему координат O′x′y′z′ с началом O′ в центре масс этой конформации и осями O′x′, O′y′, O′z′, совпадающими с главными осями инерции данной конформации (рис. 1). Алгоритм поиска системы координат O′x′y′z′ состоял в следующем. В исходной системе координат Oxyz (см. рис. 1) вычисляли координаты всех атомов текущей конформации цепи, затем координаты ее центра масс O′ и осуществляли параллельный перенос исходной системы Oxyz, совмещая начало с центром масс. В этой системе вычисляли компоненты тензора инерции [5] рассматриваемой конформации, проводили его диагонализацию и в итоге определяли направления главных осей инерции данной конформации. Надлежащим поворотом осей координат в точке O′ совмещали их с осями инерции, переходя в итоге в искомую систему O′x′y′z′. Обозначения O′x′, O′y′, O′z′ ее осей проводили одинаково в каждой конформации: ось O′x′ всегда отвечала наибольшему главному моменту инерции (то есть O′x′ – ось минимальной протяженности конформации), а ось O′z′ – наименьше- му главному моменту инерции (то есть O′z′ – ось максимальной протяженности конформации). Затем в текущей конформации цепи вычисляли разности между максимальными и минимальными проекциями атомов углерода и водорода на каждую ось O′x′, O′y′ и O′z′. Обозначали полученные разности через g1, g2, g3 соответственно. Их можно рассматривать как минимальные размеры ребер параллелепипеда (ориентированного параллельно главным осям инерции), в который конформация молекулы может поместиться целиком (см. рис. 1). В итоге компьютерного моделирования вычисляли средние величины , , и средние произведения двух размеров (в определенном смысле – это площадь поперечного сечения молекулы).

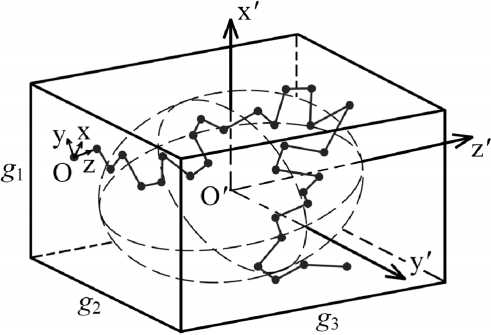
Рис. 1. Расположение «молекулярной» системы координат O′x′y′z′, которая определяется главными осями инерции O′x′, O′y′, O′z′ данной конформации цепной молекулы, представленной на рисунке только остовом – ломаной линией, соединяющей атомы углерода (•). Переход в систему O′x′y′z′ осуществлялся в каждой конформации из некоторой исходной системы координат (Oxyz). Пунктирные линии – трехосный эллипсоид инерции данной конформации цепи, O′ – ее центр масс. Главные оси инерции обозначали так, чтобы ось инерции O′z′ отвечала направлению наибольшего протяжения конформации цепи (то есть наименьшему собственному значению ее тензора инерции), а ось O′x′ – наименьшему протяжению. Величины g ₁, g ₂, g ₃ – минимальные размеры ребер параллелепипеда, построенного по следующему правилу: его грани выбраны перпендикулярно главным осям инерции данной конформации цепной молекулы (ребро g ₁ параллельно оси O′x′, g ₂ – оси O′y′, g ₃ – оси O′z′) таким образом, чтобы центры всех атомов углерода и водорода молекулы в данной конформации поместились внутри параллелепипеда

Для удобства представления результатов расчетов целесообразно указывать местоположение нескольких двойных связей в цепи с помощью лишь одного параметра. В качестве такового было использовано (аналогично работе [27]) среднее арифметическое номеров всех атомов углерода, участвующих в образовании двойных связей в цепи (атомы углерода нумеровали вдоль по цепи, начиная от одного из концевых). Этот параметр, обозначенный в работе [27] через X, характеризует положение «центра» двойных связей в цепи. Наряду с этим в ряде случаев вместо параметра X оказалось удобным использовать параметр Δ [27] – номер атома углерода, ближайшего к заданному концу цепи и участвующего в образовании первой (от данного конца цепи) двойной связи. Соответствие местоположений всех двойных связей в молекулах параметру X или параметру Δ указано в таблице.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Химическое строение любой из рассмотренных молекул идентифицируется тремя параметрами – N, d и X (или Δ), и поэтому сравнение между собой любых характеристик для разных молекул требует изучения конкуренции этих трех параметров. Учет влияния всех трех на заданную характеристику эквивалентен задаче рассмотрения 4-мерной гиперповерхности; это весьма затруднительно. Исследование 3-мерных зависимостей (поверхностей) данного свойства от отдельных пар параметров не всегда эффективно, поскольку поверхности могут пересекаться в пространстве. Поэтому наиболее целесообразно проводить анализ зависимостей свойств от одного из параметров при фиксировании двух других. На рис. 2, 3 приведены полученные в настоящей работе по итогам компьютерных экспериментов при T = 293 K зависимости оценок средних размеров , , и средней «площади поперечного сечения» от параметра X, а на рис. 4, 5 – от количества d двойных связей в цепи. Доверительные интервалы на всех представленных графиках (они меньше размеров символов) отвечают 95 %-ной надежности согласно t-распределению Стьюдента. Анализ полученных кривых позволил выявить ряд закономерностей:

• I .    При смещении центра X группы из d двойных связей от концов к середине цепи при N = Const, d = Const для всех исследованных молекул (N = 16, 18, 20, 22) с количеством d = 1–4, а также для молекул N = 22, d = 5 средний размер < g ₃> уменьшается (см. рис. 2). В молекулах N = 20, d =5 величина < g ₃> меняется незначительно.

• II .    Зависимости величин < g ₁∙ g ₂> и < g ₂> от X для молекул с количеством d = 1–3 симбатны (см. рис. 2, 3): при смещении центра X от концов к середине цепи обе величины растут. С увеличением количества d зависимости от X ослабевают: для тетраеновых (d = 4) молекул с N = 20, 22 величина < g ₁∙ g ₂> при смещении X от концов к середине еще растет, но для N = 18 уже почти не меняется. Величина размера < g ₂> тетраенов почти не зависит от X для всех изученных N (N = 16, 18, 20, 22). В пентаеновых (d = 5) молекулах зависимость от X очень слаба и для величин < g ₁∙ g ₂>,

  Соответствие положений метиленпрерывающихся двойных связей (d – их количество) в углеводородных цепях значениям параметров Δ и X

  Номера атомов C, участвующих в образовании двойных связей	Δ	X	Номера атомов C, участвующих в образовании двойных связей	Δ	X	Номера атомов C, участвующих в образовании двойных связей	Δ	X
  3, 4 (d=1)	3	3.5	3, 4, 6, 7 (d=2)	3	5	3, 4, 6, 7, 9, 10 (d=3)	3	6.5
  4, 5 (d=1)	4	4.5	4, 5, 7, 8 (d=2)	4	6	4, 5, 7, 8, 10, 11 (d=3)	4	7.5
  5, 6 (d=1)	5	5.5	5, 6, 8, 9 (d=2)	5	7	5, 6, 8, 9, 11, 12 (d=3)	5	8.5
  6, 7 (d=1)	6	6.5	6, 7, 9, 10 (d=2)	6	8	6, 7, 9, 10, 12, 13 (d=3)	6	9.5
  7, 8 (d=1)	7	7.5	7, 8, 10, 11 (d=2)	7	9	7, 8, 10, 11, 13, 14 (d=3)	7	10.5
  8, 9 (d=1)	8	8.5	8, 9, 11, 12 (d=2)	8	10
  9, 10 (d=1)	9	9.5	9, 10, 12, 13 (d=2)	9	11	3, 4, 6, 7, 9, 10, 12, 13 (d=4)	3	8
  10, 11 (d=1)	10	10.5	10, 11, 13, 14 (d=2)	10	12	4, 5, 7, 8, 10, 11, 13, 14 (d=4)	4	9
  11, 12 (d=1)	11	11.5	11, 12, 14, 15 (d=2)	11	13	5, 6, 8, 9, 11, 12, 14, 15 (d=4)	5	10
  12, 13 (d=1)	12	12.5	12, 13, 15, 16 (d=2)	12	14
  13, 14 (d=1)	13	13.5	13, 14, 16, 17 (d=2)	13	15	3, 4, 6, 7, 9, 10, 12, 13, 15, 16 (d=5)	3	9.5
  14, 15 (d=1)	14	14.5	14, 15, 17, 18 (d=2)	14	16	4, 5, 7, 8, 10, 11, 13, 14, 16, 17 (d=5)	4	10.5
  15, 16 (d=1)	15	15.5	15, 16, 18, 19 (d=2)	15	17	5, 6, 8, 9, 11, 12, 14, 15, 17, 18 (d=5)	5	11.5
  16, 17 (d=1)	16	16.5	16, 17, 19, 20 (d=2)	16	18	6, 7, 9, 10, 12, 13, 15, 16, 18, 19 (d=5)	6	12.5
  17, 18 (d=1)	17	17.5
  18, 19 (d=1)	18	18.5				3, 4, 6, 7, 9, 10, 12, 13, 15, 16, 18, 19 (d=6)	3	11
  19, 20 (d=1)	19	19.5				4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20 (d=6)	4	12

  
  
  

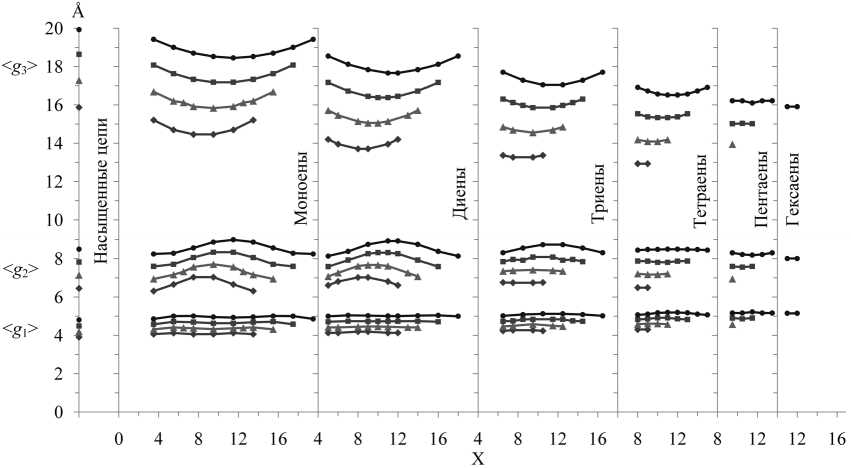
  Рис. 2. Зависимости средних размеров < g ₁>, < g ₂>, < g ₃> ребер прямоугольного параллелепипеда для невозмущенных углеводородных молекул с количеством N атомов углерода в цепи 16 (—«—), 18 (-*- ), 20 (—■— ) и 22 (—•— ), по группам молекул с одинаковым количеством d двойных связей cis (насыщенные, d = 0; моноены, d = 1; диены, d = 2; триены, d = 3; тетраены, d = 4; пентаены, d = 5; гексаены, d = 6), от местоположения в цепи «центра» метиленпрерывающихся двойных связей – параметра X. Соответствие значений параметра X положениям всех двойных связей в молекулах указано в таблице. Расчет методом МК при температуре T = 293 K

  
  
  

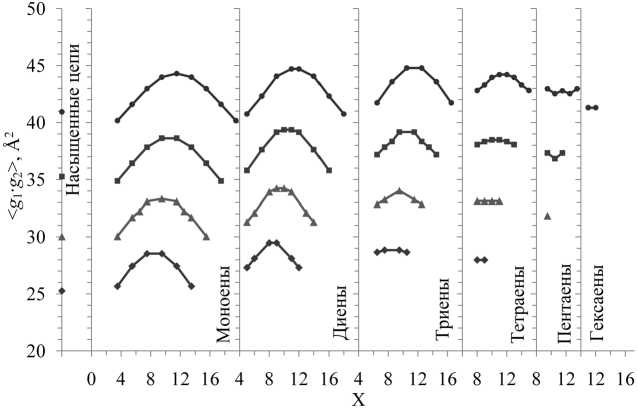
  Рис. 3. Зависимости величин средней «площади поперечного сечения» < g ₁∙ g ₂> невозмущенных углеводородных молекул от параметра X. Условия и обозначения, как на рис. 2

  
  

и для < g ₂>. Средний размер < g ₁> для молекул со всеми рассмотренными N и d почти не зависит от X.

• III .    С ростом d при N = Const, Δ = Const (для всех рассмотренных N и Δ ) величина < g ₃> уменьшается, < g ₁> увеличивается (хотя и слабо), а величины < g ₂>, < g ₁∙ g ₂> изменяются немонотонно (см. рис. 4, 5), и результат зависит как от N, так и от Δ . Немонотонность в большей степени проявляет зависимость от d величины < g ₁∙ g ₂>, а для цепей с Δ = 3 она “S-образна” (имеет участки убывания и возрастания). В каждой совокупнос-

• ти молекул с одинаковым N, которые содержат разное количество d, от нуля до максимально возможного (d = 0, 1, 2, …, dmax), метиленпрерываю-щихся двойных связей с одинаковым расположением Δ = 3, существует молекула с количеством двойных связей d1 (не обязательно равным нулю), площадь которой минимальна, и молекула с количеством двойных связей d2 (не равным dmax), площадь которой максимальна; конкретные значения d1 и d2 зависят от N (см. рис. 5).

• IV .    С ростом N при d = Const, Δ = Const средние значения величин < g ₁>, < g ₂>, < g ₃>, < g ₁∙ g ₂>

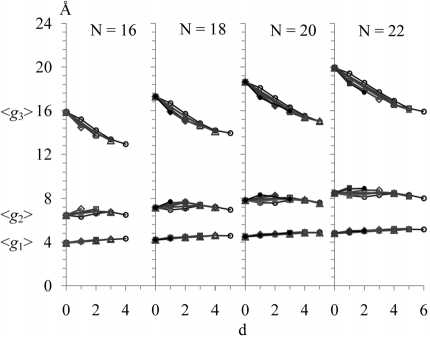
Рис. 4. Зависимости средних размеров < g ₁>, < g ₂>, < g ₃> (спэ-нов, рис. 1) от количества d двойных связей cis для невозмущенных углеводородных молекул с параметром Δ = 3 ( -6- ), 4 ( д ), 5 ( —), 6 (-в— ), 7 ( -е- ), 8 (-*- ), 9 (-•- ), 11 ( □ ) по группам молекул с одинаковым количеством N атомов углерода в остове цепи. Параметр Δ – это номер атома углерода, участвующего в образовании первой двойной связи от конца цепи. Соответствие значений параметра Δ положениям всех двойных связей в молекулах указано в табл. 1. Расчет методом МК при температуре T = 293 K

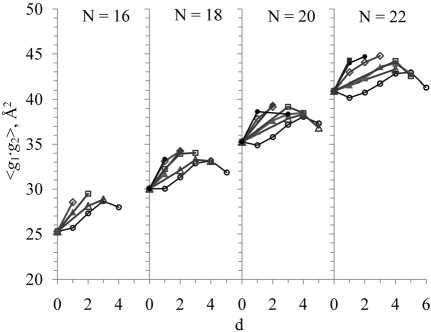
Рис. 5. Зависимости величин средней «площади поперечного сечения» < g ₁∙ g ₂> от количества d двойных связей cis для невозмущенных углеводородных молекул. Условия и обозначения, как на рис. 4

растут для всех рассмотренных вариантов цепей с параметрами d = 0–5 и Δ = 3–11 (данные не представлены), что и ожидалось для коротких цепей в невозмущенном состоянии [9].

Обсуждаемые зависимости отражают сложность и неоднозначность результата конкуренции во влиянии на свойства молекул трех структурных параметров. Однако анализ молекулярных основ внутреннего вращения в цепях рассматриваемого строения позволяет понять причины основных тенденций и влияния того или иного параметра структуры на свойства цепи. Ряд причин обсужден ниже.

Наиболее вероятной в каноническом ансамбле конформацией цепи является конформация, отвечающая глобальному минимуму ее потенци- альной энергии. Такая конформация насыщенной цепи – это «транс-зигзаг» [3], [9], когда цепь предельно вытянута, а все атомы углерода лежат в одной плоскости. Из соображений симметрии следует, что ось O′z′ конформации «транс-зигзаг» лежит в плоскости углеродного остова цепи и направлена от атома углерода одного ее конца к атому углерода другого; ось O′y′ также принадлежит плоскости остова и перпендикулярна оси O′z′, а ось O′x′ перпендикулярна плоскости остова; размер g3 соответствующего параллелепипеда будет максимальным, а g1<, , , что согласуется с данными рис. 4. Зависимость расчетных характеристик от местоположения метиленпрерывающихся двойных связей в цепях также объяснима. Действительно, пусть d = 1 и двойная связь в молекуле расположена у одного из концов цепи. Тогда большинство атомов углерода приходится на насыщенный участок, а в наиболее низкоэнергетической конформации они лежат в одной плоскости, влияние «свернутости» малого концевого участка на конформацию цепи минимально. Если же d = 1 и двойная связь в молекуле расположена вблизи середины цепи, то тенденция к «свернутости» конформации, наоборот, проявляется максимально: молекула имеет два наиболее протяженных насыщенных участка (по обе стороны от двойной связи), их конформации «транс-зигзаг» принадлежат двум разным плоскостям, под углом друг к другу. Очевидно, размер g3 второй моноеновой молекулы будет в итоге существенно меньше (а размеры g2, g1 – больше), чем соответствующие размеры первой. Такие же соотношения следует ожидать и для средних значений , , , что подтверждается результатами расчетов (см. рис. 2). Можно также ожидать, что обсуждаемое влияние двойной связи будет возрастать по мере перехода от предельного варианта 1 к варианту 2, то есть при смещении двойной связи от любого конца цепи к ее середине (см. рис. 2). Эти же соображения объясняют сходные зависимости расчетных характеристик от X, наблюдающиеся в полиеновых молекулах (d > 1), с учетом того, что с увеличением d в цепи влияние местоположения двойных связей ослабевает, поскольку участок цепи, на котором можно изменить положения двойных связей, сокращается.

Среди всех изученных в настоящей работе молекул в Θ-условиях существуют совокупности, молекулы в которых, будучи различными по строению (то есть имея различные N, d, Δ ), обладают тем не менее соизмеримыми, сравнительно близкими «продольными» размерами < g ₃>. Если задавать различные интервалы значений < g ₃> (по оси ординат на рис. 2), то можно выделять совокупности молекул, размеры < g ₃> которых попадают в заданные интервалы. Зададим, например, отклонения ±5 % от величины < g ₃> молекулы 16:0. Можно убедиться, что в этот интервал значений попадают величины < g ₃> молекул 18:1ω9 cis , 18:2ω6 cis , 18:3ω3 cis , 20:3ω6 cis , 20:4ω6 cis , 20:5ω3 cis , 22:5ω3 cis , 22:6ω3 cis и ряда других (см. рис. 2); эти молекулы образуют одну из упомянутых совокупностей. Параметры N, d, Δ молекул с метиленпрерывающимися двойными связями cis указаны здесь согласно «ω-номенклатуре», через сокращенную формулу N: dω Δcis . Важно отметить, что все молекулы в приведенном примере, как оказалось, входят в список таких цепей, которые встречаются в биологических мембранах в качестве компонентов молекул фосфолипидов наиболее часто [2], [12], [25]. Очевидно, в бислоях в жидкокристаллическом состоянии продольные размеры этих цепей (проекции на нормаль к поверхности бислоя) должны быть согласованы друг с другом. Результаты наших расчетов свидетельствуют об их «предрасположенности» к аналогичной ком-плементарности и в невозмущенном состоянии.

Подобный результат ранее уже был отмечен в литературе при МК-моделировании и расчетах величин < g ₃> молекул [27]. При этом использованная в [27] модель цепи и алгоритм МК существенно отличались от таковых настоящей работы

• [7] . В частности, при генерировании конформаций цепей в [27] учитывалась взаимозависимость каждых 2 последовательных торсионных углов основной цепи, а не 3, как в настоящей модели [7]; поверхность потенциальной энергии молекулярных фрагментов, зависящих от пар углов, разбивалась в [27] на 1 600 равновероятных состояний, тогда как энергии фрагментов, зависящие от троек углов, были разделены в [7] на 1 000 000 равновероятных состояний; различны также и параметры силовых полей, использованные в [27] и [7]; наконец, расчеты < g ₁>, < g ₂>, < g ₃> в [27] осуществлялись с учетом только атомов углерода, а в настоящей работе по модели [7] – с учетом атомов углерода и водорода. В итоге и численные значения соответственных величин < g ₁>, < g ₂>, < g ₃> одних и тех же молекул, рассчитанные в [27] и в настоящей работе, различаются существенно (на ~20–35 %). Однако перечисленные выше закономерности качественно, в главном сохраняются, и в этом состоит их основная ценность. Устойчивость обсуждаемых зависимостей и тенденций к деталям используемой модели и к параметрам силового поля свидетельствует о том, что они отражают фундаментальные соотношения между структурой и свойствами данных молекул, в основе которых лежат характерные особенности внутренних вращений в цепях рассмотренного химического строения.

Совокупности цепей, отвечающих разным диапазонам размеров < g ₃>, могут, по-видимому, примерно соответствовать основным жирнокислотным составам липидов в мембранах разных биологических объектов, разных органов и тканей.

Прогнозирование свойств молекул заранее заданного строения представляет собой весьма сложную задачу, поэтому компьютерное моделирование конкретных молекул и выявленные в настоящей работе зависимости имеют большую ценность.

• * Работа выполнена при поддержке программ президента РФ «Ведущие научные школы» (гранты НШ-1642.2012.4, НШ-1410.2014.4).

MONTE CARLO EVALUATION OF HYDROCARBON CHAIN MOLECULES’ SHAPE