Оценка фрактальности финансовых временных рядов с помощью показателя Херста

Обычно, говоря о размерности объекта, имеют в виду его топологическую (или геометрическую) размерность, которая не отражает извилистости (изломанности) линии. Например, на рис. 1 изображены три объекта, для которых топологическая размерность равна 1.

Рис. 1. Различные объекты с одинаковой топологической размерностью

Так как топологическая размерность нечувствительна к гладкости кривой, то ее использование в исследовании финансовых временных рядов ограничено. Очевидно, более естественно оценивать размерность объекта по степени заполнения им фазового пространства (в простейшем случае – листа бумаги) на котором изображена траектория исследуемой динамической системы. Приняв размерность полностью заполненного листа за 2, получим, что размерность реальной кривой будет дробной – фрактальной.

Одним из наиболее точных методов определения дробной размерности является, так называемый, R/S анализ [1]. В настоящей работе предложена методика определения фрактальных размерностей финансовых временных рядов на базе упрощенного (модифицированного) алгоритма расчета показателя Херста.

Постановка задачи

Исследуется временной ряд:

r = r (t) (t = 0, T ), например, котировки акций эмитента (см. рис. 2).

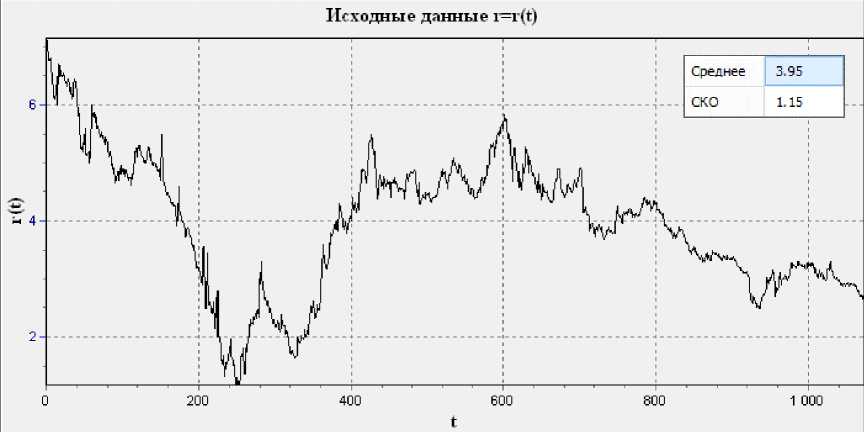
Рис. 2. Исходные данные

Требуется определить его фрактальную размерность

Обработка и исследование исходных данных

С целью исключения зависимости последовательных измерений приведем исходные данные к так называемым «логарифмическим прибылям»:

p = p ( t ) = In

r (t) r(t-1)

⁽ t = 1, T )

Преобразованные данные

после

центрирования и нормирования представлены на рис. 3. Там же приведены значения среднего и среднеквадратичного отклонения.

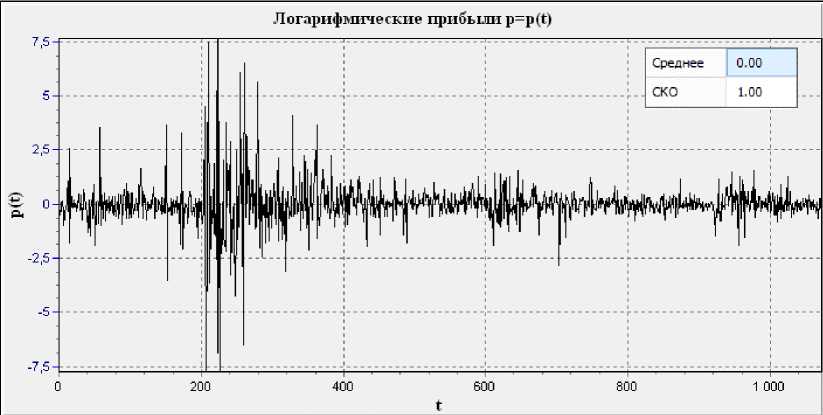
Рис. 3. Логарифмические прибыли

Для проверки нормальности распределения рассчитаем асимметрию A :

_   M ( X - M ( X ) ) ³

A s   /                    2 \^2

(M(X -M(X)) )

и эксцесс E :

M (X - M (X ))4

E k =------------ - 3 .

(M (X - M (X ))2)

На рис. 4 представлена гистограмма распределения для исследуемых данных с нанесенной на них кривой нормального распределения, а также значениями асимметрии и эксцесса.

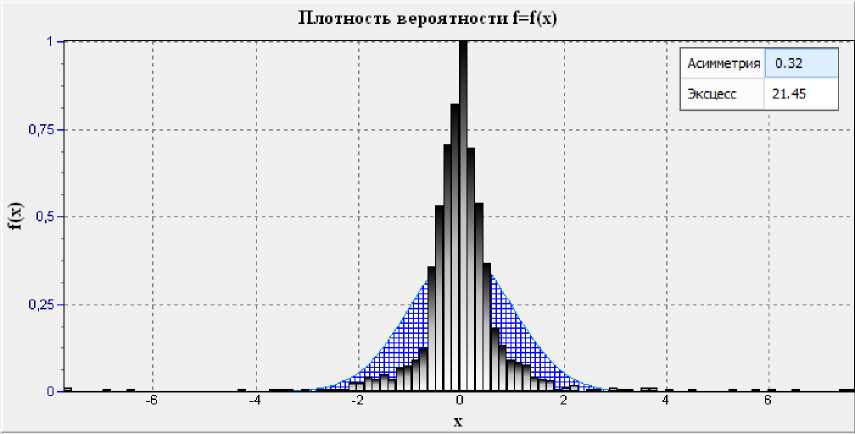
Рис. 4. Гистограмма распределения

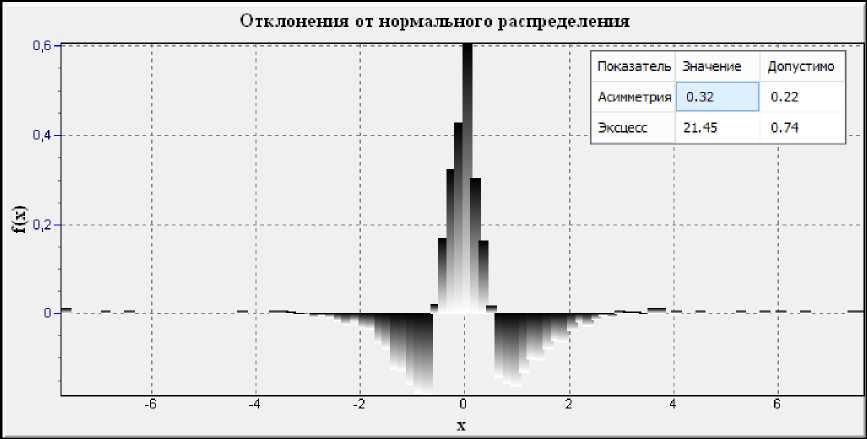
Рис. 5. Отклонения от нормального

На рис. 5 показано отклонения эмпирического распределения от нормального.

Величины критических значений отклонений асимметрии и эксцесса от соот- ветствующих показателей нормального распределения рассчитываются по формулам:

по асимметрии:

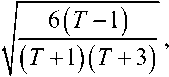
по эксцессу:

24 ( T - 3)( T - 2) T

(T-1)2 (T + 3)(T + 5)

Таким образом обрабатываемые данные имеют распределение, которое нельзя отнести к нормальному закону.

Алгоритм

Рассмотрим упрощенный (модифицированный по сравнению с классическим [1]) алгоритм расчета показателя Херста.

Vt = T o , T

• 1.    p T =- ^ p ( t ) — среднее

• 2.    P t ( t ) = ^ ( p ( i ) — p t ) ; ( t = 1, t ) - накопленная сумма отклонений от среднего i = 1

• 3.    R = R ( t ) = max P ( t ) — min P ( t ) ^— размах t e [ 1, x ] ^T            t е [ 1, т ] ^T

• 4.    5 = 5 (^T) = |      ^ ( p ( t ) ^— p t ) I ^{- СКО}

• 5.    Отношение R = R ( t ) - определяет точку ( х_л , y ) = ( ln T ,ln ( R/S ) ) ; ( j = t — t₀ + 1 )

T t = 1

t

t           2^2

< ^{T — 1} t = 1                 J

Пусть R/S = ( c t ) H , где c - параметр, H

– показатель Херста тогда

Показатель Херста может быть найден как МНК оценка b углового коэффициента линейной регрессии y = a + bx (рис. 6).

y = a + P x ; ( y = In ( R/ S ) , a = H In c , в = H , x = In t )

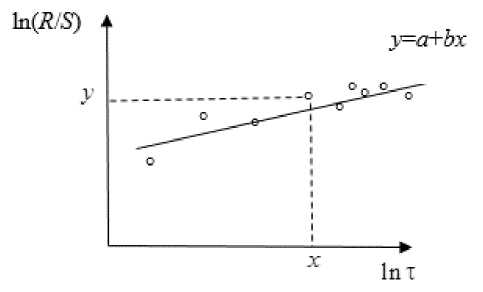
Рис. 6. Схема R / S анализа

Оценка размерностей

Фрактальная размерность (рассчитанная на базе показателя Херста) найдется так:

D„ = 2 — H .

H

Применительно к финансовым данным фрактальная размерность может интерпретироваться как степень влияния информации на временной ряд. Значение D является рыночным индикатором и может служить показателем риска инвестиций.

Значение DH = 1,5 означает случайное блуждание (в этом случае справедлива гипотеза эффективного рынка), в данном случае события некоррелированы, все новости уже учтены рынком.

Величина 1 < D„ < 1,5 означает, что се-H годняшние события и полученная информация будет продолжать учитываться рынком еще и некоторое время спустя. Причем это не просто последовательная корреляция, а функция долговременной памяти, которая обуславливает информационное влияние в течение больших периодов времени. Такой временной ряд называют персистентным (трендоустойчивым) – он имеет более гладкую, менее за- зубренную линию чем при случайном блуждании.

Величина 1,5 <  D_H <  2 характеризует систему, более подверженную переменам нежели случайное блуждание. В этом случае временной ряд является антиперси-стентным, который волатилен, т.е. более изменчив, чем ряд случайный. Для финансовых данных такие ряды не характерны.

Еще одним показателем фрактальности временных рядов является размерность, полученная Мандельбротом [2]:

D m =

H

Если размерность D есть мера «зазубренности» или неровности временного ряда, то величина D по сути – фрактальная размерность пространства вероятностей – измеряет высоту пика гистограммы и толщину ее хвостов (лептоэксцесс). Согласно гипотезе эффективного рынка D всегда равно 2, в соответствии с гипотезой фрактального рынка 1 <  D_M <  2 .

Высокий пик распределения свидетельствует о наличии «памяти» на рынке и, следовательно, говорит о применимости технического анализа. С другой стороны, «толстые хвосты» распределений определяют высокую вероятность появления на рынке событий от 4 ст и более. Это, так называемые, «крахи» (спекулятивные пузыри), которые вызваны умышленным сбросом или скупкой ценных бумаг.

Учет лептоэксцесса позволяет прогнозировать как поведет себя система при коллапсе рынка.

Корреляционное соотношение

Влияние настоящего на будущее может быть выражено корреляционным соотношением:

С_н = 2 ^{2 H - 1} - 1

Величина - 0,5 <  С_н <  0 свидетельствует о том, исследуемый ряд является анти-персистентным, который называют «возврат к среднему». Если система демонстрировала рост на данном этапе, то, скорее всего в следующем периоде будет спад, и наоборот (отрицательная корреляция). Такой ряд более волатилен, чем случайный, так как состоит из частых реверсов спад-подъем.

Если С_н = 0 , то ряд является случайным – настоящее не оказывает влияние на будущее, а вероятностные распределения подчинены нормальному закону. В этом случае подтверждается гипотез эффективного рынка, события случайны, некорре-лированы, информация уже учтена и обесценены рынком.

При 0 <  С_н <  1 временной ряд будет персистентным и последние события имеют более сильное влияние, чем предыдущие. В этом случае события сегодня будут иметь значение завтра, т.е. полученная информация учитывается рынком и некоторое время спустя. Это долговременная память, которая обуславливает информационное влияние в течение больших периодов времени.

Пример расчета

Определим показатель Херста для исходных данных, представленных на рис.3. Оценка параметров линейной регрессии осуществлялась на основании выражений:

' b = ^ЬЦ

• < x2-(_x) • a = y - bx

На рис.7 приведены результаты расчетов.

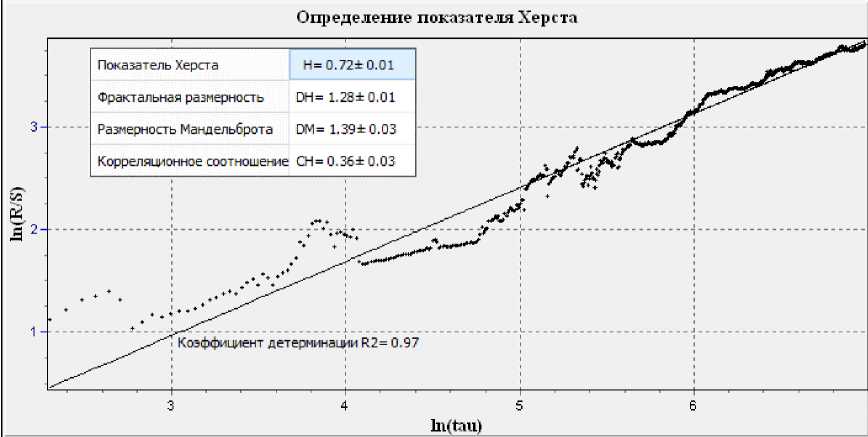
Рис. 7. Определение показателя Херста по линейной регрессии

Среднеквадратичная ошибка для параметра b находилась по формуле:

sb

,( T - 2 )( x2-(x )2),

где f = a + bx

Абсолютная ошибка Д₆ = t_ss_b , тогда доверительный интервал составит b ±Д_Ь , т.е. 0,72 + 0,01.

Коэффициент          детерминации

• 2      ( У - f )

R = 1 -=--- — равен 0,97, что подтвер-

• У2-(y)

ждает удовлетворительное качество ап проксимации исходных данных прямой.

Выводы

Предложенный модифицированный метод расчета показателя Херста позволяет определить характеристики фрактальности временных рядов с помощью алгоритма, имеющего невысокую трудоёмкость. Рассмотренные фрактальные размерности могут быть использованы в системах поддержки принятия решений для выработки управляющих воздействий при работе, например, на фондовой бирже.