Оценка функции когерентности пульсовых сигналов при многоканальной пульсометрии

Полисфигмографическим методом в [1, 2] обнаружено наличие тесной связи между формой и отдельными элементами сфигмограмм сонной и лучевой артерий как в состоянии покоя, так и при функциональных пробах, изменяющих условия системной гемодинамики. Таким образом, в [1] получено качественное, а в работе [2] количественное доказательство принадлежности сфигмограммы лучевой артерии по форме к группе центральных сфигмограмм. Особую актуальность вопрос о соответствии СФГ лучевой артерии о форме группе центральных сфигмограмм принимает при реализации комплексной программы по объективизации и автоматизации пульсовой диагностики тибетской медицины.

Известно, что пульс в организме человека является интегральным процессом, отражающим состояние многих органов и функциональных систем. Форма артериального пульса зависит от силы и скорости сердечных сокращений, ударного объема крови и артериального давления, эластичности и тонуса стенок артерии и т.д. Исследование пульса с запястья обеих рук человека используется в восточной медицине для диагностики функционального состояния внутренних органов [3]. Для анализа пульсовых волн можно привлечь весь богатый аппарат обработки сигналов, созданный до настоящего времени.

Одним из основных методов математического анализа пульсовых сигналов является спектральный анализ. В статье [4] в качестве критерия, соответствующего границе между нормой и патологией, предложен энергетический коэффициент ЭК, определяемый как отношение усредненного энергетического спектра W пульсового сигнала в полосе частот от 1 до 10 Гц ( W1 ) к соответствующей величине в полосе частот от 10 до 50 Гц ( W2 ) [4]:

ЭК = W1/W2, в котором частота f = 10 Гц принята как пограничная частота при определении различных параметров для оценки состояния внутренних органов человека и его функциональных систем. Важную роль в спектральном анализе случайных процессов играет так называемая функция когерентности сигналов, которая может служить мерой линейности связи между сигналами [5]. Наличие аддитивного и/или мультипликативного шума при регистрации сигналов, а также нелинейность канала распространения сигнала, приводит к уменьшению значений функции когерентности, в то время как при отсутствии шума и идеальной линейности системы функция когерентности равна 1.

Факторами, снижающими величину функции когерентности, являются [6]:

• -    шум, который суммируется с полезными сигналами на разных участках распространения сигна-

• ла по исследуемому каналу и в измерительных трактах;

• -    погрешности расчета спектральных функций, определяемые неучтенной нелинейностью канала

распространения и измерительных трактов.

Таким образом, необходимо произвести оценку некоррелированных частотных составляющих сигналов при многоканальной регистрации пульсовых сигналов. Наиболее существенным и простым методом определения некоррелированных частотных составляющих является оценка функции коге- рентности.

Функция когерентности сигналов, по аналогии с коэффициентом корреляции, несет информацию о степени корреляции, то есть о степени линейной взаимосвязи двух процессов, но только в частотной области. Если колебательные процессы статистически независимы, то при всех значениях частоты γxy2 ≡ 0. Если γxy2(f) ≡ 1 то процессы x(t) и y(t) полностью когерентны. Присущее каждому значению частоты значение функции когерентности можно рассматривать как возведенное в квадрат значение коэффициента корреляции, отображающего степень линейной зависимости между двумя процессами – с учетом того, что оценки собственных спектров соответствуют вариации переменных ве- личин, а оценка взаимного спектра соответствует ковариации этих величин.

Для анализа степени линейной взаимосвязи двух пульсовых сигналов в частотной области использована нормированная функция когерентности [5]:

γ x ² y ( f ) =

J S xy ( f ) ²

S xx ( f ) S yy ( f )

где S xy (f) , S xx (f), S yy (f) – взаимные спектральные плотности .

Исследования проводились с помощью Автоматизированного пульсодиагностического комплекса [3]. Запись производилась синхронно с шести датчиков пульса, установленных на запястье обеих рук человека. Датчики пульса устанавливаются на традиционных точках пальпации согласно канонам тибетской медицины. Частота дискретизации пульсовой волны составляла 200 Гц, длина реализаций – 100 сек.

Результаты расчетов приведены на рис. 1. Здесь по оси абсцисс отложена частота f в Гц, а по оси ординат нормированная функция взаимной когерентности γ xy² ( f ).

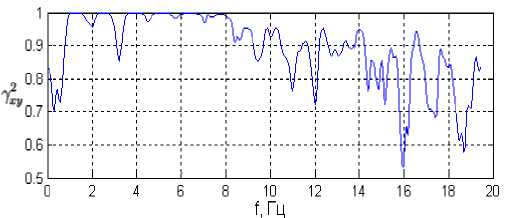
стьях руки человека

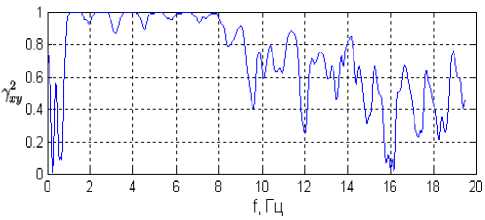
Рис. 1. Функция взаимной когерентности двух сигналов а) На одном запястье руки человека; б) На двух запя-

Как видно из представленных рисунков, в частотном диапазоне от 0,6 Гц до 8 Гц функция когерентности γ xy² ( f ) принимает значения, близкие к 1, что означает совпадение гармонических составляющих в указанном диапазоне частот спектров двух пульсовых сигналов, зарегистрированных в разных точках пальпации на лучевых артериях человека. Поэтому частоту f=8 Гц будем считать пограничной частотой при определении различных параметров, в том числе и при расчете модифицированного энергетического коэффициента МЭК.

Динамический диапазон функции когерентности постоянный и составляет 0 ≤ γ xy² ( f ) ≤ 1. Частотный диапазон и разрешение по частоте сохраняются от исследуемых спектров. Учитывая, что анализ

В.В. Бороноев, Б.З. Гармаев, В.Д. Омпоков. Корреляция спектральных и статистических характеристик пульсового сигнала при заболеваниях сердца подлежат частотные составляющие, имеющие очень сильную взаимосвязь (γ2 ≥ 0,95), возможно в последующем производить цифровую фильтрацию.

Цифровая фильтрация предусматривает только два значения частотных составляющих функции когерентности

( / 2,2 ( f ) >  0,95) = 1

( y 22 ( f ) <  0,95) = 0

. Иными словами, создается маска для преобразования спектра

когерентной выходной мощности, в которой остаются частотные составляющие только с высоким уровнем функции когерентности, а остальные частотные составляющие отфильтровываются.

Таким образом, корреляционный анализ пульсовых сигналов в частотной области показал, что в диапазоне от 0,6 Гц до 8 Гц функция взаимной когерентности двух сигналов принимает значения, близкие к 1. Это позволяет частоту f = 8 Гц считать пограничной частотой при определении различных параметров для оценки состояния внутренних органов человека и его функциональных систем в отличие от рекомендуемой в работе [4].