Оценка функционального состояния больного гипертонической болезнью на основе математического моделирования

Несмотря на большое количество работ, опубликованных за последние годы и посвященных гипертонической болезни (ГБ), эта важная проблема остается актуальной в связи с ее высокой распространенностью и смертностью [3, 6, 7]. Своевременная диагностика является важным элементом лечебно-профилактической системы, позволяющей методологически грамотно практикующему врачу осуществлять весь комплекс мероприятий по контролю за артериальной гипертонией (АГ). Поэтому повышение качества диагностики является по-прежнему актуальной задачей [2, 5]. Известно, что обладающий врачебной интуицией опытный врач может, суммируя результаты комплекса клинических методов обследования, высказать достаточно точное суждение о состоянии больного и его прогноз в отношении исходов заболевания. Однако, такой анализ клинических данных не исключает определенного, пусть и невысокого уровня ошибок, а во-вторых доступен далеко не каждому специалисту. Исходя из этого факта, решающим в объективизации функционального состояния и прогнозировании развития болезни может стать создание математических моделей, позволяющих с высокой степенью вероятности предсказать возможные пути развития и становления заболевания [1, 4, 8, 9].

Впервые математический метод определения прогноза был разработан при инфаркте миокарда S. Schn-ur,1953 г. Шагом вперед была система R. Norris и соавт., 1969, построенная с применением ЭВМ. В дальнейшем эту проблему разрабатывали К. Хартман, 1977, И.М. Гельфанд и соавт.,1994, Л.А. Лещинский, 1998г., В.Н. Ардашев, 1999 и др. В то же время известны лишь единичные работы, посвященные математическому прогнозированию функционального состояния больных ГБ. Вышесказанное позволяет считать продолжение исследований в данном направлении актуальным.

Цель работы – построение математической модели, предсказывающей оценку функционального состояния больного гипертонической болезнью в процессе проводимых лечебно-профилактических мероприятий.

В настоящей работе использована собственная разработка математической модели, предусматривающая унификацию ряда критериев оценки состояния тяжести больных ГБ. В качестве теоретической базы использованы положения математической статистики, теории вероятностей и планирования эксперимента.

Обследовано 99 человек, из них 69 больных ГБ I – II ст. (основная группа) по критериям ВОЗ/МОАГ и 30 здоровых пациентов (контрольная группа), являющихся в данном исследовании эталоном.

Алгоритм исследования включал в себя следующие этапы:

• 1)    формализация данных и представление их в виде, удобном для статистической обработки на ЭВМ;

• 2)    выделение существенных и исключение слабо влияющих факторов на исход заболевания;

• 3)    построение математической модели, нацеленной на прогнозирование функционального состояния больного ГБ;

• 4)    верификация разработанной модели на контрольной группе больных;

В процессе исследования проведен предварительный корреляционный анализ всех факторов, влияющих на состояние психосоматического статуса.

Структуризация и формализация данных, характеризующих психосоматический статус пациентов, проведенная на основе дискриминантного анализа, позволили ранжировать 58 дискретных признаков и выделить 6 наиболее важных из них (табл. 1).

Верификация дискретных признаков на основе математического метода подтвердила выбор признаков,

Табл. 1. Описание переменных, характеризующих состояние больных ГБ

Переменная	Название переменной	Размерность
Х 1	Уровень тревоги (Тр)	баллы
Х2	Индекс напряжения (ИН)	усл.ед.
Х 3	Хронотропный резерв сердца (ХРС)	усл.ед.
Х 4	Инотропный резерв сердца (ИРС)	усл.ед.
Х 5	Индекс эффективности (ИЭ)	усл.ед.
Х 6	Показатель умственной работоспособности (ПУР)	сек.

Табл. 2. Матрица корреляции показателей клинико-функциональных показателей в группах

Переменная х1 х2 х3 х4 х5 х6 х1 1 0,42 0,31 0,35 0,39 0,45 х2 0,42 1 0,42 0,36 0,35 0,31 х3 0,31 0,42 1 0,30 0,31 0,32 х4 0,35 0,36 0,30 1 -0,38 -0,33 х5 0,39 0,32 0,31 -0,38 1 0,8 Х6 0,45 0,31 0,41 -0,33 0,8 1 характеризующих деятельность различных функциональных систем, влияющих на формирование ГБ.

Этими признаками явились: показатель тревожности (Тр), отражающий уровень эмоциональной напряженности и личностной дезинтеграции; индекс напряжения (ИН) – важнейший показатель вегетативной регуляции ЦНС; показатели хронотропного (ХРС), инотропного резервов сердца (ИРС), индекса эффективности (ИЭ), характеризующие состояние центральной гемодинамики и миокардиального резерва и, наконец, показатель умственной работоспособности (ПУР), выявляющий уровень динамической психической деятельности. Совокупность всех признаков этих функций, по нашему мнению является мерой оценки функционального состояния больного ГБ.

На основе корреляционного анализа установлены взаимосвязи выделенных дискретных факторов больных основной группы (ОГ), влияющих на их функциональное состояние и прогноз развития заболевания. При этом коэффициент корреляции считался значимым для данного объема выборки (69 больных) уже при r>0,308. В результате корреляционного анализа установлено, что изучаемые дискретные признаки мало зависят друг от друга и могут быть использованы в дальнейшем в регрессионной модели. Полученные данные подтвердили правомочность выделения признаков по степени их информативности и взаимосвязи в формировании подхода к оценке функционального состояния больных ГБ.

В целях соблюдения частоты эксперимента поиск корреляции между клинико-функциональными показателями был повторен на контрольной группе. Параллельно был проведен анализ корреляции дискретных факторов между собой в обеих группах (табл. 2).

Обобщающие результаты корреляционного анализа свидетельствуют о том, что ряд признаков обладают высокой степенью корреляции. Это следующие величины: х1 – уровень тревоги, х2 – индекс напряжения; х6 уровень умственной работоспособности.

Следующим этапом разработки был поиск решения задачи по получению конечной формулы определения функционального состояния пациента в ходе наблюдения и лечения.

В результате расчетов была построена первичная линейная модель на основной группе (69 больных).

Формула расчёта выглядит следующим образом: P= K+1,08*Х1+0,16*Х₂+1,90*Х3-0,14*Х4+0,65*Х5+0,29*Х6; К= -125;

где P – эквивалентный информатор для диагностики рассматриваемого состояния; 1-6 – номера показателей симптомов в порядке ранжирования; ai – постоянные коэффициенты дискриминантной функции; xi – значения диагностических признаков исследуемого; K – константный показатель.

В результате решения уравнения исследователь получает числовое значение «P» в усл. ед., которое, по существу, является интегральным показателем функционального состояния (ИПФС).

После получения линейной формулы проведены расчеты на основной и контрольной группах с целью получения средних значений оценки функционального состояния пациентов. Был использован материал, полученный в результате трехмесячного наблюдения за пациентами обеих групп. Результаты клинико-психологических показателей, определяемых еженедельно, представлены в табл. 3 и табл. 4.

Диапазон значений ИПФС для больных основной группы находится в пределах от 149,9 усл. ед. до 199,5 усл. ед. Диапазон значений ИПФС для контрольной группы (здоровые лица) находится в пределах от 101,2 усл. ед. до 149 усл. ед. Анализ результатов наблюдения за пациентами основной группы выявил определенную тенденцию изменений показателей ИПФС в сторону его оптимального уровня, что позволяет использовать их для распознавания функционального состояния и уровня адаптации в конкретный период наблюдения. Результаты контрольной группы свидетельствуют о достаточно стабильном уровне функционального состояния здоровых лиц, что подтверждает оптимальный уровень параметров (эталон), к которому следует стремиться в результате лечения.

Диапазон значений ИПФС у пациентов основной и контрольной групп наглядно представлен на Рис. 1. Таким образом, диапазон значений ИПФС для больных ГБ колеблется в пределах 150–200 усл. ед. и указывает направление в сторону оптимального уровня функционального состояния (менее 150 усл. ед.).

Для определения индивидуального прогноза функционального состояния больного ГБ построены графики,

Табл. 3. Результаты клинико-психологических показателей больных основной группы в периоды еженедельного обследования в течение 3-х мес.

	1-ый месяц				2-ой месяц				3-ий месяц
	1-ая нед	2-ая нед	3-ая нед	4-ая нед	1-ая нед	2-ая нед	3-ая нед	4-ая нед	1-ая нед	2-ая нед	3-ая нед	4-ая нед
Х 1	36,5	35,7	34,6	33,2	32,0	31,8	30,5	29,3	28,4	27,9	27,1	26,5
Х 2	264,8	251,1	244,2	239,5	235,8	232,2	234,3	218,1	203,5	182,3	174,2	168,6
Х 3	91,2	90,0	89,1	88,6	87,8	86,9	86,2	85,7	85,0	84,1	83,4	82,3
Х 4	26,6	26,9	27,2	27,6	28,0	28,3	28,7	29,1	29,5	29,8	30,2	30,5
Х 5	81,4	81,5	80,0	77,6	76,1	75,7	74,2	74,8	75,3	75,9	76,7	77,5
Х 6	75,6	74,7	73,8	72,9	72,0	71,1	70,2	69,3	68,4	67,5	66,6	65,8
P	199,5	193,1	187,9	182,8	178,1	175,2	171,6	167,0	162,2	156,6	153,3	149,9

Табл. 4. Результаты клинико-психологических показателей пациентов контрольной группы в периоды еженедельного обследования в течение 3-х мес.

1-ый месяц 2-ой месяц 3-ий месяц 1-ая нед 2-ая нед 3-ая нед 4-ая нед 1-ая нед 2-ая нед 3-ая нед 4-ая нед 1-ая нед 2-ая нед 3-ая нед 4-ая нед Х1 16,2 15,6 15,3 14,4 14,1 13,6 13,6 12,4 12,0 12,3 12,5 10,9 Х2 163,0 162,3 160,3 155,3 151,7 148,3 140,0 133,7 129,0 127,7 123,2 120,0 Х3 68,1 62,3 61,9 60,3 59,7 59,5 58,5 58,1 57,8 49,0 48,3 47,0 Х4 25,8 25,6 24,1 24,0 23,7 23,2 22,5 22,1 21,4 21,1 20,4 19,6 Х5 140,8 140,1 143,8 143,2 145,7 148,1 146,9 147,3 148,5 149,4 150,2 150,5 Х6 48,1 46,4 45,0 44,7 43,3 42,5 43,1 42,5 42,1 42,9 42,2 42,1 P 149,6 138,5 136,4 135,7 130,1 130,3 126,6 123,6 118,8 107,6 105,6 101,2 характеризующие изменения величины интегрального показателя (ИПФС) в динамике, по которым можно прогнозировать результаты лечения. Изменения данного показателя за период 3-х месячного наблюдения представлены в виде кривых на рис. 2.

Выявленная зависимость позволяет, сравнив величину ИПФС конкретного пациента с эталонным графиком, определить вероятностный прогноз и оценить уровень его состояния в конкретный период наблюдения.

Диагностическая информативность интегрального показателя дополнительно проверена на независимой контрольной группе из 20 больных ГБ, рандомизированной с основной группой по основным клиническим показателям. Были рассчитаны следующие характеристики: точность предложенной методики прогноза (82%), ее специфичность (89%), чувствительность (81%). Представленные данные свидетельствуют о том, что разработанная модель обладает высокой эффективностью. При этом интегральный показатель (ИПФС) ориентирован на предсказания функционального состояния больного ГБ.

Построенные графики, отражающие диапазон значений ИПФС и его динамику в зависимости от времени наблюдения, по существу в нашем исследовании являются номограммами, с помощью которых исследователь может оценить уровень ИПФС конкретного больного.

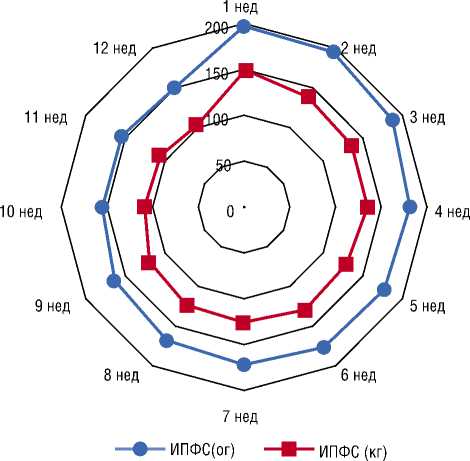
Рис. 1. Диапазон значений интегрального показателя функционального состояния (ИПФС) больных основной и контрольной групп

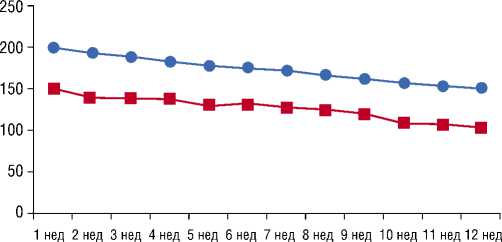
♦— ИПФС(ог) ■ ИПФС (кг)

Рис. 2. Взаимосвязь интегрального показателя функционального состояния (Р) и времени наблюдения. По оси абсцисс – время в неделях. По оси ординат – значения интегрального показателя в усл. ед. 1 – кривая, характеризующая изменения интегрального показателя в основной группе в ходе лечения. 2 – кривая, характеризующая изменение интегрального показателя в контрольной группе в ходе наблюдения

Таким образом, разработанный метод математического анализа расширяет диапазон системного подхода к диагностике артериальной гипертонии и обеспечивает более высокий уровень результатов прогностических решений. Важным является возможность использования разработанного интегрального показателя в прак- тической деятельности для индивидуальной оценки функционального состояния конкретного больного ГБ и дальнейшего прогноза его состояния.