Оценка и прогноз динамики коррупции в Российской Федерации методами аналитического выравнивания

В настоящем исследовании проводится статистическая оценка уровня коррупции в Российской Федерации и дается её прогноз на 2021 – 2023 годы. В качестве исходных данных были взяты количество набранных баллов в Индексе восприятия коррупции (Corruption Perception Index), который ежегодно составляется международной организацией Transparency International.

Для количественной оценки динамики коррупции в России по данным Индекса восприятия коррупции за 1997 – 2020 г.г. по вышеприведенным данным, были построены модели временных рядов по уравнениям линейной, экспоненциальной, логарифмической, степенной функций, а также функций парабол второго и третьего порядков. Для оценки качества и точности построенных трендовых моделей по каждой из них были рассчитаны коэффициенты детерминации R ² и средние ошибки аппроксимации A (таблица 1).

Таблица 1.

Трендовые модели динамики коррупции в России по данным Индекса восприятия коррупции за 1997 – 2020 г.г.

Результаты расчетов показывают, что наиболее адекватной является модель построенная по уравнению параболы третьего порядка, так как у нее наибольший коэффициент детерминации R ² и приемлемый уровень средней ошибки аппроксимации A . Коэффициент детерминации R ² = 0,5 показывает, что модель является качественной и пригодной для практического применения. Значение средней ошибки аппроксимации A = 8,7% <  10% свидетельствует о том, что модель является точной. Все остальные трендовые модели являются статистически незначимыми, так как коэффициенты детерминации, рассчитанные по ним, оказались значительно меньше 0,5.

Фактические баллы России в Индексе восприятия коррупции (ИВК) и результаты аппроксимации по трендовой модели, построенной на основе уравнения параболы третьего порядка y_t = 21,88 + 0,169 • t - 0,022 • t ² + 0,0011 • t ³ представлены на рисунке 1.

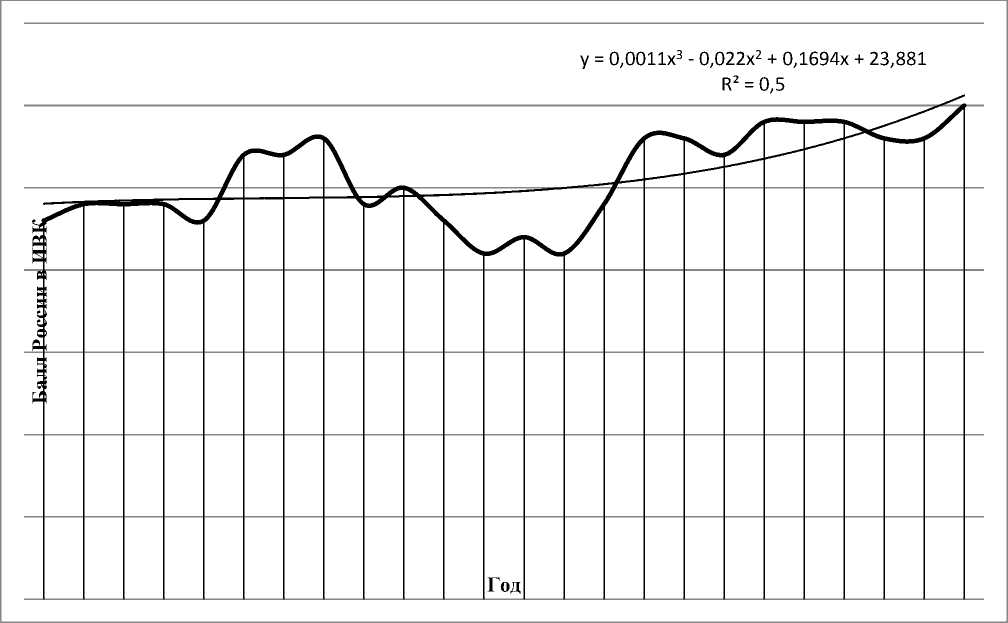
Рис. 1. Фактические баллы России в ИВК и результаты аппроксимации по трендовой модели, построенной на основе уравнения параболы третьего порядка y_t = 21,88 + 0,169 • t - 0,022 • t ² + 0,0011 • t ³ .

Трендовая модель, построенная по уравнению параболы третьего порядка ( y_t = 21,88 + 0,169 • t - 0,022 • t ² + 0,0011 • t ³ ) была использована для построения прогноза количества присвоенных России баллов в Индексе восприятия коррупции в 2021 – 2023 г.г. Расчеты показали, что с вероятностью 90% число баллов, полученных Россией в Индексе расположится в следующих доверительных интервалах:

28,7 <  У 2021 г. <  34,4;

29,9 <  У 2022 _г. <  35,6;

31,2 <  У 2023 г. <  37,0.

Таким образом, прогноз показал вероятную положительную динамику полученных Россией баллов и её места в Индексе восприятия корруп- ции.