Оценка импульсной характеристики речевого тракта методом реконструкции математической модели динамической системы по порождаемому временному ряду

Решение задачи идентификации личности по голосу имеет большое значение для ограничения доступа к информации в комплексных системах безопасности. Определение импульсной характеристики речевого тракта полезно в задачах идентификации и верификации диктора по голосу. В настоящее время существует множество различ- ных подходов к решению проблем идентификации и верификации.

В [1] представлена модель речевого тракта, состоящая из передаточной функции резонансной системы и генератора импульсов сигнала возбуждения. Основными параметрами здесь являются частота основного тона, параметр тон/шум, звонкость, подъем основного тона. Но знание этих параметров недостаточно, так как полученные величины параметров искажены погрешностями вычислений и неблагоприятных внешних воздействий (внешние шумы).

Для получения дополнительных характеристик используется метод линейного предсказания [2]. Коэффициенты модели линейного предсказания играют роль дополнительной информации о речевом сигнале. И вместе с оценкой частоты основного тона, энергии исследуемого сигнала используются для решения задачи идентификации личности по речевым сигналам. Такой подход дает неплохие результаты (ошибки от 1% до 2%). Но на практике ошибки могут вырасти в 100 и более раз.

В [3] представлен иной подход к исследуемой проблеме – задача обратной фильтрации. Этот подход позволяет получить параметры колебаний голосовых связок, определяющих форму импульсов голосового возбуждения. Основной проблемой данного подхода является неустойчивость модели линейного предсказания к типу используемых микрофонов.

Основной целью данной работы является получение оценки импульсной характеристики речевого тракта, когда роль параметров голосового возбуждения играют сегменты этого же речевого сигнала, взятые с некоторой временной задержкой. Достижение данной цели базируется на разработке подхода решения обратной задачи речевой акустики с помощью процедуры реконструкции математической модели динамической системы по порождаемому временному ряду. Под динамической системой будем понимать процесс речеобразования, под временным рядом будем понимать речевой сигнал, являющийся реализацией динамической системы.

Все представленные в данной работе вычисления проводились на материале гласных звуков.

2.    Постановка обратной задачиречевой акустики

Речевой процесс может быть описан интег ральным уравнением Фредгольма [4]

+∞

J x ( t - T ) h ( r ) d T = y ( t ) , - w <  t < +w,

-∞

здесь x ( t ) - возбуждение в голосовой щели как в источнике, h ( t ) - импульсная характеристика речевого тракта, y ( t ) - речевой выход. В (1) искомой является функция h ( t ) , при известных x ( t ) и y ( t ) . Аналитическое решение уравнения

(1) можно представить в виде ОПФ [4], которое не дает точных решений. Поэтому речь может идти об оценках решения уравнения (1).

Теоретической основой процедуры реконс- трукции являются положения нелинейной динамики. Любой хаотический сигнал можно представить в виде линейной комбинации некоторых коэффициентов и функционального базиса, который можно рассматривать как передаточную функцию исследуемого процесса. Аргументом данной функции являются вариации этого же сигнала, полученные с помощью специальных методов. Таким образом, постановка обратной задачи речевой акустики и процедура реконструкции, примененная к речевому сигналу, эквивалентны.

• 3.    Оценка импульсной характеристики речевого тракта методом реконструкции математической модели динамической системы по порождаемому временному ряду

  Процедура реконструкции математической модели динамической системы по некоторым данным предполагает прохождение ряда этапов. Первый этап – предварительная обработка данных. Разобьем исходный речевой сигнал на сегменты длиной 200 отсчетов (около 10 мс при частоте дискретизации 22050 Гц).

Второй этап предполагает восстановление компонент векторов состояния модели исследуемой динамической системы – реконструкция фазового портрета. Определим размерность реконструируемой модели D = 3. В случае получения неадекватной модели размерность увеличивается. Далее воспользуемся методом последовательного дифференцирования [5-6]

xw=

v(ti),^T dt

dl4J dtD-1

i = 1 ,N , (2)

где N – объем выборки. Но данный метод неустойчив относительно входных данных [5].

Обойти существующие трудности позволяет следующий подход. Каждую последующую компоненту будем получать из интеграла по переменному верхнему пределу от предыдущей компоненты. На рис. 1 представлены проекции фазовых портретов речевого сигнала на плоскость ( x 1 , x 2 ) .

Рис. 1. Проекции фазовых портретов для методов последовательного дифференцирования и интегрирования соответственно

Теперь переходим к третьему этапу реконструкции. В общем виде имеем

P

f(x ) = X ck фк (x ) ,

k=1

x – вектор состояния исследуемой системы, зависящий от времени, ck – последовательность параметров, фк (x) - система базисных функций, P – пространство параметров. Представим f в виде алгебраического многочлена. Реконструируемая модель имеет вид

ttt

J Xdt = X 1 ; J X 1 dt = x ₂ ; J X 2 dt = x ₃ ;

X = f ( X 1 ,X 2 ,X 3 ) = C 0 + C 1 X 1 + c ₂ X 2 + c ₃ X 3 +

+ c ₄ X 1 X 2 + c ₅ X 1 X 3 + c ₆ x ₂ x ₃ + c ₇ X 1 X 2 x ₃ +

22   2   22

+ C 8 X 1 + C 9 X 2 + C 10 X 3 + C 11 X 1 X 2 + C 12 X 1 X 3 +

^{+ c} 13 ^X 1 ^X 2 ^X 3 ^{+ c} 14 ^X 1 ^X 2 ^{+ c} 15 ^X 1 ^X 2 ^X 3 ^{+ c} 16 ^X 2 ^X 3 ⁺

2        2          222

^{+ c} 17 ^X 1 ^X 3 ^{+ c} 18 ^X 2 ^X 3 ^{+ c} 19 ^X 1 ^X 2 ^X 3 ^{+ c} 20 ^X 1 ^X 2 ⁺

22      22     22

+ C 21 X 1 X 2 X 3 + c ₂₂ X 1 X 3 + c ₂₃ X 1 X 2 X 3 +

22     22222

c ₂₄ X 2 X 3 + C 25 X 1 X 2 X 3 + C 26 X 1 X 2 X 3 .

Здесь x – речевой сигнал; x ₁ , x ₂ , x ₃ – возбуждение в голосовой щели, c ₀ ,..., c ₂₆ - импульсная характеристика речевого тракта.

Для определения значений коэффициентов в (4) воспользуемся МНК [5; 7]

1 ^N

8 2 = — ^[ x - f ( x_px₂,x₃ )] ² ^ min .   (5)

^N i=1

Последний этап процедуры реконструкции предполагает исследование реконструированной модели на адекватность исследуемому объекту.

Вычислим квадратный корень из (5). Величина ε может служить показателем качества модели.

4.    Тестирование реконструированной модели речевого процесса

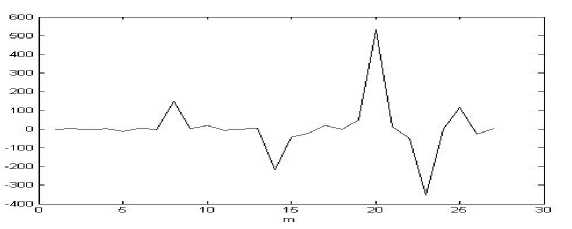
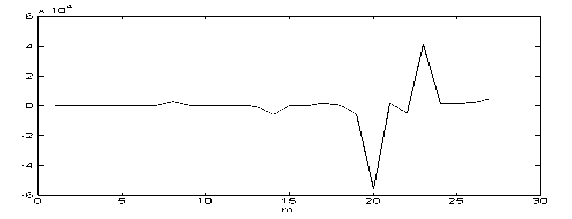
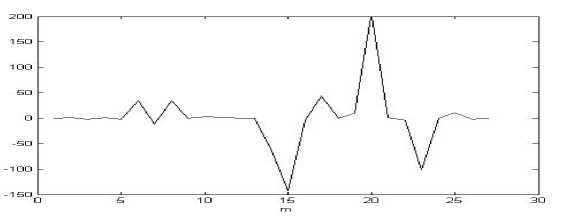
В тесте принимало участие 11 человек. Каждый произносил звук «э» три раза. Далее полученные сигналы усреднялись. Затем каждый из 11 усредненных сигналов сегментировался по 200 отсчетов. Выбирались те сегменты, где размах амплитуды наибольший. К полученным сегментам применялась процедура реконструкции математической модели динамической системы по порождаемому временному ряду. На рис. 2 представлены результаты оценки импульсной характеристики для 5 участников эксперимента.

Полученные оценки коэффициентов модели речевого процесса (4), состоящей из передаточной функции в виде алгебраического многочлена и оценок возбуждения в голосовой щели, будем интерпретировать, как оценки импульсных характеристик голосового тракта, отражающие индивидуальные особенности речевой акустики при произношении различных звуков.

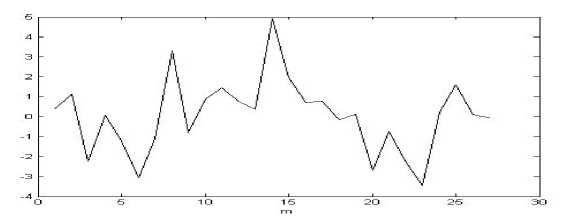
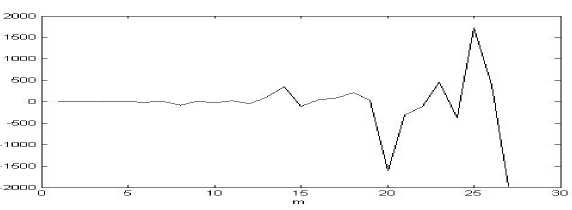
Рис. 2. Оценки импульсной характеристики для звука «э» по сегментам с наибольшим размахом амплитуды для каждого образца усредненных сигналов

5.    Заключение

В работе показано применение процедуры реконструкции математической модели динамической системы по порождаемому временному ряду к речевым сигналам. Тестирование модели речевого процесса проводилось над одиннадцатью испытуемыми по результатам неоднократного произношения звука «э». Полученные оценки импульсной характеристики речевого тракта, с аппроксимируемой передаточной функцией (4) отражают индивидуальные особенности речевой акустики для каждого из испытуемых и могут быть расширены для других сегментов и звуков.

Полученные оценки можно применять для решения практических задач.