Оценка информационных возможностей амплитудно-модулированных сигналов

Самарский государственный аэрокосмический университет

Рассмотрены информационные возможности амплитудно-модулированного сигнала. Получена математическая модель амплитудно-модулированного сигнала, основанная на энтропийном подходе. Сделан вывод о том, что количество информации, переносимой сигналом, определяется как разность значений энтропий без модуляции и с модуляцией. Полученные результаты позволяют сравнить информационные возможности различных типов модуляции и выбрать оптимальный вариант.

Энтропийный подход к анализу возможностей и ограничений технических средств позволяет получать оценки их свойств инвариантные к аппаратной реализации, что делает такие оценки достаточно фундаментальными.

Рассмотрим информационные возможности амплитудно-модулированного (АМ) сигнала. Модулированный сигнал является произведением несущего колебания

UH(t) = UH • sinwi и модулирующего колебания

^U M ^(t) = ^U M • sin I — | = K M • U h • sin l — I,

V n j                 V n j

HM

1 n *          1

= ^- EE ( - 1) g ^{- 1} •

ⁿ p = ig = -

K

■ I 2n m • sin l — • p V n

g

. (4)

Ряд (4), сходящийся, т.к. для этого зна-

кочередующегося ряда выполняется признак

Лейбница ( К М <  1):

K _M

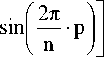
g

>

g

K _M

. I 2n

• sin l-- p

V n

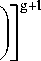
g +1

Если ограничить число членов ряда (4) значением b, то модуль остатка ряда:

где n – кратность частот несущего и модулирующего сигналов; KМ =0..1 – коэффициент модуляции.

Энтропия синусоидального несущего сигнала равна:

IRbl <^k

v I 2n

K m • sin l-- p

V n b + 1

-1 b+1

.

Максимальное значение |Rb| имеет место при р/n = 0,25

H_h(U) = ln(nn_H/2).

Средняя (на периоде модулирующего колебания) энтропия амплитудно-модулиро-

max |R ь | <  (K m ) ^{b + 1} / b + 1.

Если max |R b | будет в £ раз меньше, чем первый член ряда (4), то минимальное значение числа “b” соответствует условию (2):

ванного сигнала:

H AM

1 n ,

= - E^^/2

n p = 1

- + K m

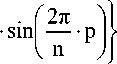
, (1)

(min b) + 1 = £ • K ^{(min b)}

где р – номер периода несущего колебания

внутри периода модулирующего сигнала.

Уравнение (1) можно представить следующим образом:

При £ = 100 и K <  0,4 , получим (min b) <  4.

Более точно это значение можно определить с помощью вычисления частичной

суммы ряда (4) вместо первого члена.

Тогда выполнится следующее условие:

H am = ln ( nU H /2 ) + H m ,     ( 2)

n

H m = - E ln n p = 1

1 , v ( 2n

1 + K _M • sin l-- р

V n

maxlR bl <¹ ε

KM

234 K_M  K_M  K_M

--1---- 234

.

Уравнение (3) запишем в виде ряда Тейлора:

Уточнение с помощью уравнения (5), сохраняет значение (min b) <  4

Следовательно, с погрешностью, не превышающей 1%,

2                                    34

Un        (-п -  1 Г       (-п Yl    1 Г       (-п YI hm =~Х—м• sin   p , I km•sin~I +ri km-sinl — I .

n p = i         I ⁿ   J  2n p = i L       I ⁿ JJ    3n p = i L       I ⁿ

нии (6) равна 0.

Второй ряд из уравнения (6) преобразу-

ется аналогичным образом:

Для суммирования рядов, входящих в (6), представим тригонометрическую часть этих рядов в комплексной форме [2]:

j2π sin I -np| = Im(en )p = VP, к n J j2π где Z = e n .

1 V I - n — I K M ^sinl — p - n p = 1 L        к n .

2 π

n

^{-           -} i

| =      ] n - Re

¹         4 n I

Z² (Z² n - 1 ) Z ^- - 1

где

Z 2n– 1 = cos(4р) + jsin(4р) – 1 = 0 и, следовательно:

_n                   2 K 2

• -    I^{[ -}M^{sin ( -n/} n • p ^)] = -^.

• -    p = 1                            4

При этом первый ряд из уравнения (6)

будет иметь вид:

nn

- £ K_Msin | —p | = —M • I_m( ^ Z p ).

n;^ к n J n     ;= 1

Преобразуя подобным образом третью и четвертую части уравнения (6), окончатель-

но получим:

Понятно, что уравнение (7) представля-

H _M

24  2

^—m ^3— m _  ^—m i , ^{3   -} rim

U---3-----4"^{1 +} 8^-M .⁽¹⁰⁾

ет собой геометрическую прогрессию.

1 “       I П )   -_{M T}

- I ^-M^sin l -p | = — • I m n p = 1       к n J n

Z(Zⁿ - 1) Z - 1

В последнем уравнении сомножитель (Z n-1) равен:

Zⁿ - 1 = e^j-n - 1 = cos-n + jsin-n - 1 = 0, а отношение Z(/Z – 1) преобразуется следующим образом:

Z _ 1 - cos ( - n/n) - j sin ( - n/n)

Z 1 =        - [ 1 - cos ( - n/n) ]       • ⁽⁹⁾

Преобразуем мнимую часть уравнения

- sin ( - n / n ) _ 1

- [ 1 - cos ( - n / n )]     -

tg ( - n / n )

и получим, что сумма первого ряда в уравне-

Значения HМ, рассчитанные по последней формуле, представлены в графической форме на рис. 1 , из которого видно, что зависимость HМ от KМ близка к квадратичной и может быть аппроксимирована с погрешностью не более ±2% выражением:

H m ^ 0,-55 • — m^- .

Количество информации, переносимое сигналом, определяется как разность значений энтропий без модуляции и с модуляцией [1].

Поэтому количество информации, переносимое амплитудно-модулированным сигналом IАМ = - НМ.

Следует отметить, что соотношение (10) не зависит от кратности частот несущего и модулирующего сигналов ”n”, что позволя-

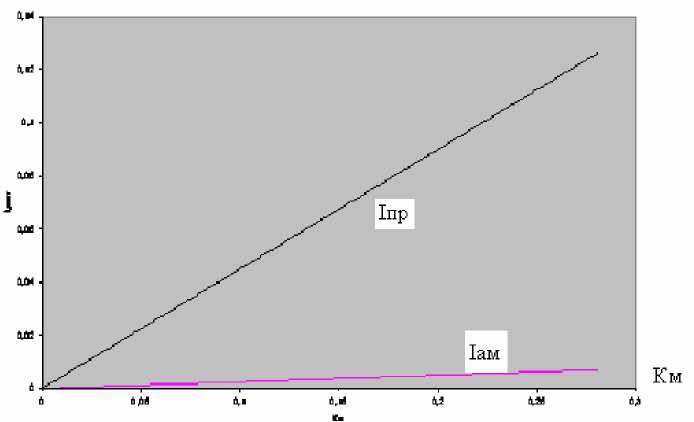
Рис. 1. Зависимость энтропии от коэффициента модуляции

ет применить полученные результаты для различных амплитудно-модулированных сигналов при любых значениях “n” .

Полученные результаты позволяют сравнить информационные возможности различных типов модуляции и объективно осуществлять выбор оптимального варианта.