Оценка использования геофизического метода VLF для определения мощности торфяного месторождения

Торфяники являются распространенным элементом минерально-сырьевой базы регионов России. Однако многие субъекты РФ отличаются разной степенью изученности торфяного фонда. Торфяные месторождения аккумулируют большие запасы углерода и играют важную роль в формировании глобального климата, биосферы и гидрологии. Высокая степень изученности торфяных запасов является одной из предпосылок научно обоснованного и экономически целесообразного управления водно-болотными угодьями. Для экономически эффективной хозяйственной деятельности предприятие, разрабатывающее торфяную залежь, должно быть уверено в наличии достаточного и качественного объема промышленных запасов торфа [1].

Интенсивная геологическая разведка торфяных месторождений проводилась лишь в советский период, в настоящий момент такие исследования не проводятся ввиду их высокой стоимости и трудоемкости. Проектные организации при подготовке технического проекта разработки торфяного месторожде- ния используют устаревшую информационную базу торфяных фондов 1952, 1989 и 2000 гг. Большим недостатком содержащейся в торфяных фондах информации является отсутствие данных о мощности конкретной залежи (глубине торфа), ее пнистости (количестве и толщине горизонтов погребенной древесины) и виде минерального подстилающего грунта. По этой причине знания о количестве, масштабах и мощности торфяников, их пространственной изменчивости в российских регионах сильно различаются. Это также, вероятно, связано с различными стандартами, инструментами и методами измерения.

Степень изученности торфяного фонда Татарстана составляет 78%. Цифры по общей площади и количеству торфяников в Татарстане различны. Например, в торфяном фонде 1952 г. площадь предполагаемого фонда торфяных запасов составляла 20 тыс. га, а количество месторождений 608 ед. Данные торфяного фонда 1989 г. сообщают о площади 20,6 тыс. га, а по информации торфяного фонда 2000 г. уже 30 тыс. га и 900 ед. месторождений [1, 2]. Тем не менее толщина и другие характеристики тор-

I ГОРНЫЕ НАУКИ

I Ж И ТЕХНОЛОГИИ

2020;5(3):224-234

МИСиС

Национальный исследовательский технологический университет

фяных залежей сильно различаются, а у некоторых месторождений сообщаются не полностью. Кроме того, многие торфяные залежи в Татарстане граничат с месторождениями углеводородных ресурсов.

В данной работе авторы при исследовании торфяного месторождения предлагают использовать геофизический метод, который позволяет определить мощность торфяной залежи с высокой точностью результата. Геофизический метод основан на использовании электромагнитной волны очень низкой частоты, поэтому он еще называется методом VLF-EM, или VLF. Метод VLF-EM изначально был разработан для подводной навигации. Тем не менее он также используется для геофизической разведки месторождений благодаря своей способности проникновения сквозь поверхность земли и распространения на очень большое расстояние.

Распространение VLF-EM в пределах земли может вызвать любой подземный провод- ник, производящий вторичное электромагнитное поле, которое может быть обнаружено с помощью приемника VLF. Метод VLF фактически использует оборудование, которое имеет возможность приема и измерения разницы между первичным и вторичным электромагнитным излучением с точки зрения фазы или поляризации. Измеряемая электромагнитная энергия, излучаемая подземным проводником, зависит от его проводимости и удельного сопротивления. Торфяной, минеральный подстилающий грунт и слой погребенной древесины имеют разную проводимость и, следовательно, будут иметь разную поляризацию [3].

Цель данного исследования заключалась в оценке возможности использования метода VLF для исследования изменчивости глубины торфа и определения пнистости торфяного месторождения.

Методика проведения исследования

Исследование проводилось на торфянике «Озеро Белое», расположенном в Тукаев-ском районе Татарстана. Это одно из крупных по объему запасов месторождение, участки которого отличаются по глубине торфа, то есть А – очень глубокий торф (свыше 3 м), B – глубокий торф (1,5 – 3 м) и C – мелкий торф (0–1,5 м) (рис. 1). «Озеро Белое» – типичное для условий Татарстана высокозольное месторождение низинного вида травяной группы, озерного типа образования. Это единственное разрабатываемое с 2009 г. месторождение торфа, используемого для сельскохозяйственных нужд.

Применяемые в исследовании инструменты: торфяной шнек, карта торфяной залежи, GPS, приемник VLF-EM и компьютер с установленным программным обеспечением Inv2DVLF [4–6]. Основными собранными данными являлись: глубина торфа и данные VLF. Данные VLF состояли из синфазной и квадратурной составляющих сигнала [7]. Синфазная составляющая сигнала – это величина поляризованного угла вторичной обмотки поля к вертикальному первичному полю. В свою очередь, квадратурная составляющая сигнала – это отношение эллиптических осей к плоскости поляризации [6, 8]. Измерения VLF соответствовали общему методу геофизической разведки ОНЧ. Измерение было проведено в 16 линиях в трех направлениях исследований. На каждом участке торфяной залежи (А, В) было 5 линий, на участке С – 6 линий. Длина трассы геофизического исследования составляла от 200 до 500 м, в то время как интервалы между линиями были от 10 до 20 м. Глубина торфа измерялась прямым методом по скважинам, которые были расположены на каждые 80 м во всех трассах геофизического исследования. В некоторых местах, где изменчивость глубины торфа резко увеличивалась, пространство между скважинами было уменьшено (рис. 1). Собранные данные VLF были проанализированы с использованием метода NAMEMD для устранения эффекта шума в наблюдениях [9, 10]. Очищенные от шумового фона данные были затем инвертированы с использованием Inv2DVLF [6, 11], для того чтобы получить оценку 2D удельного сопро-

I ГОРНЫЕ НАУКИ

• I    Ж И ТЕХНОЛОГИИ

  2020;5(3):224-234

  
  

  МИСиС

  Национальный исследовательский технологический университет

  
  

тивления вдоль линий каждого участка торфяной залежи.

Обсуждение полученных результатов

Программное обеспечение Inv2DVLF оценивает значения синфазности и квадратур и предсказывает вертикальные последовательные удельные сопротивления вдоль каждой трассы геофизического исследования. Предсказанный информационный массив удельного сопротивления состоит из 8 вертикальных z-позиций на глубину: 0,5 м, 1,1 м, 1,52 м,

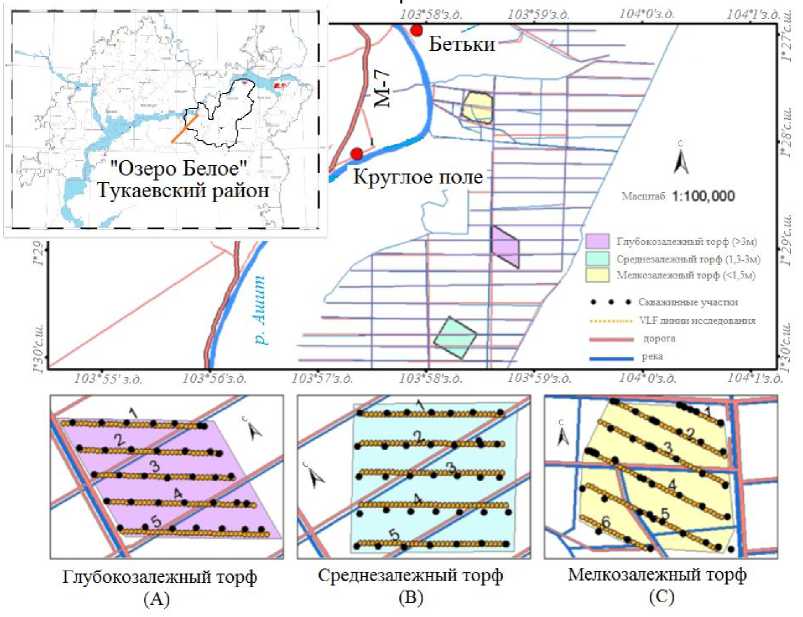
Рис. 1. Карта района исследования и места отбора проб

Прогнозируемые удельные сопротивления по каждой линии трассы геофизического исследования были интерполированы по вертикали с использованием геостатистического программного обеспечения для создания 2D вертикальных плоскостей. Результат интерполяции в виде удельного сопротивления представлен на рис. 3, а толщина торфа отображается линией на каждом графике. Имеющиеся на линии пики (зеленый цвет) показывают количество и толщину горизонтов погребенной древесины. Торфяная залежь в естественном состоянии представляет собой пористую, насыщенную влагой, разную по плотности с различными включениями (пни, камни, линзы воды, песка, глин и т.д.)

• 2,2 м, 2,58 м, 3,15 м, 3,6 м и 4,72, м. Эти глубины могут незначительно отличаться в зависимости от частот, используемых в методе VLF, и начальных удельных сопротивлений. В процессе исследования начальное удельное сопротивление по методу VLF составляло 15 Ом-м. На рис. 2 показано положение предсказанных удельных сопротивлений по Inv2DVLF.

осадочную породу, в которой наблюдается весьма большая изменчивость электропроводности [3]. Соответственно, электропроводимость торфа, различных включений и подстилающего грунта будет отличаться [11–14]. Так, например, древесина в сухом состоянии обладает высоким электрическим сопротивлением и является диэлектриком, а находясь в торфяной залежи, древесина пропитывается водой и теряет свои диэлектрические свойства. Кроме того, сопротивление разных пород дерева также различно. Так, например, сопротивление сосны при влажности 20% составляет 3 · 108 Ом/см, а березы – 4,2 · 1010 Ом/см, при влажности 100% сосна – 1,8 · 105 Ом/см, а береза – 2 · 107 Ом/см.

2020;5(3):224-234

Чем больше влажность залежи (80–90 %), тем      которых можно определить мощность горизон- ниже сопротивление и выше электропроводимость [11]. Таким образом, удельная электропроводимость торфа имеет сильную корреляцию с его свойствами (влажность, степень разложения, пнистость, ботанический и агрохимический состав, зольность и т.д.). Ввиду вышесказанного возникает резонный вопрос: «Как различить электропроводимость торфа, погребенной древесины и подстилающего минерального дна?» [15–17]. При исследовании торфяной залежи методом VLF при интерпретации полученных сопротивлений на графиках, представ- тов погребенной древесины. Визуально достаточно трудно распознать корреляцию между толщиной торфа и удельным сопротивлением по методу VLF (рис. 3).

В основном большинство графиков указывают на то, что удельное сопротивление уменьшается с ростом глубины торфяной залежи. Однако это не соотносится с толщиной торфа. При этом ни один из графиков не показывает прямой корреляции между мощностью торфяных слоев и удельным сопротивлением.

ленных на рис. 3, появляются пики, по высоте

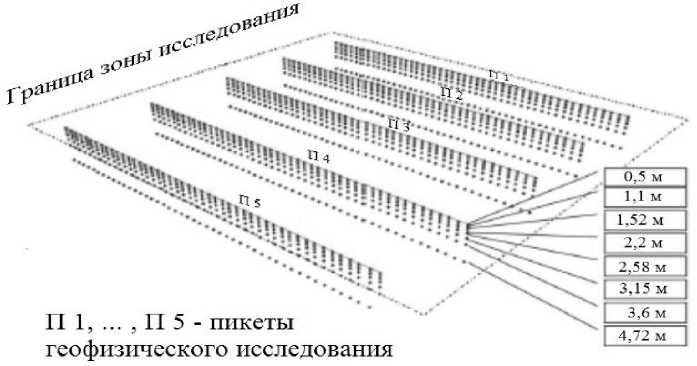
Рис. 2. Расположение мест измерения удельных сопротивлений вдоль поперечников, генерируемых программным обеспечением Inv2DVLF (каждая точка измерения методом VLF дает 8 точек расчетного удельного сопротивления торфяного массива (эти глубины несущественно различаются в зависимости от частоты используемой в VLF и начального удельного сопротивления, определенного перед обработкой)

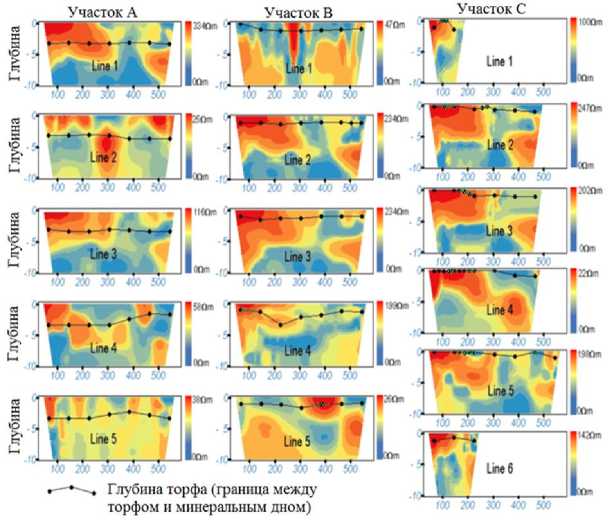
Рис. 3. Вертикальные плоскости удельного сопротивления по участкам торфяной залежи

2020;5(3):224-234

Изменения удельного сопротивления      древесины там отсутствуют. Объяснение дан- очень различны по всем трем участкам торфяной залежи. На участке А высокое удельное сопротивление (красный цвет) больше скон- центрировано в верхнем слое, а в других слоях оно слабее. Кроме того, на большинстве графиков показано высокое удельное сопротивление в начале линий. На линиях с 1-й по 5-ю участка С зеленым цветом выделены пики в областях скачков высокого сопротивления, что позволяет утверждать наличие «островков» погребенной древесины средней мощностью 0,5 м. На 4-й и 5-й линиях участка В также имеются пиковые значения удельного сопротивления, которые показывают, что слой погребенной древесины незначительный (по сравнению с участком С). Здесь следует отметить, что лесом покрыто 19% территории Татарстана, а на торфяных месторождениях участки древесной растительности встречаются «островками». Ввиду этого торфяные месторождения Татарстана обладают низкой пнистостью. Высокая пнистость встречается на мелкозалежных месторождениях или «островками» в поверхностных горизонтах торфяной залежи, как, например, на исследуемом месторождении «Озеро Белое». Торф на месторождении «Озеро Белое» имеет озерное происхождение, и самая большая глубина определена прямым методом по скважине в центре месторождения – 5м. Участок А с глубиной до 4,72 м расположен в границах реликтового озера, поэтому горизонты погребенной ных по удельному сопротивлению и толщине торфа, а также статистическое описание и оценка представлены в табл. 1. Для статисти- ческого анализа использовались метод ANOVA и тест HSD Тьюки [18–20] (критерий подлинной значимости), который отслеживает частоту ложноположительных результатов с поправкой на эффект множественных сравнений. Это означает, что если производится проверка на уровне 0,05, то при выполнении всех парных сравнений вероятность получения одного или нескольких ложноположительных результатов составляет 0,05.

В целом среднее удельное сопротивление имеет тенденцию уменьшаться по мере роста толщины слоя торфа. Это показывают данные в табл. 1. Линейный график на рис. 4, а показывает тенденцию снижения удельного сопротивления с глубиной, представляющей три участка и среднее из общих данных. Полные строки показывают похожую тенденцию снижения, которую можно интерпретировать по уравнению:

участок А:

у = -4,849 ln % + 35,709, R ² = 0,8421; (1) участок B:

у = -6,305 lnx +40,915, R 2 = 0,9453; (2) участок C:

у = -7,255 lnx +43,428, R 2 = 0,9318; (3) среднее значение:

у = -6,1361пх + 40,017, R 2 = 0,919,   (4)

где у – удельное сопротивление; х – толщина торфяного горизонта, м.

Таблица 1

Прогнозируемое удельное сопротивление по исследуемым участкам торфяного месторождения «Озеро Белое»

Глубина	Участок А		Участок В		Участок С
	Значимость	Стандартное отклонение	Значимость	Стандартное отклонение	Значимость	Стандартное отклонение
0,5	33,72	50,92	39,94	49,56	41,98	48,98
1,1	33,97	44,41	37,49	43,56	40,26	41,88
1,52	30,75	33,95	32,82	33,44	35,28	32,57
2,2	26,01	22,11	28,60	23,10	28,01	22,24
2,58	25,06	23,96	25,48	21,24	24,97	18,22
3,15	21,57	18,42	22,93	22,75	21,92	16,27
3,6	14,81	9,85	16,90	11,16	16,61	9,09
4,72	18,58	6,57	17,58	6,81	16,89	5,43

2020;5(3):224-234

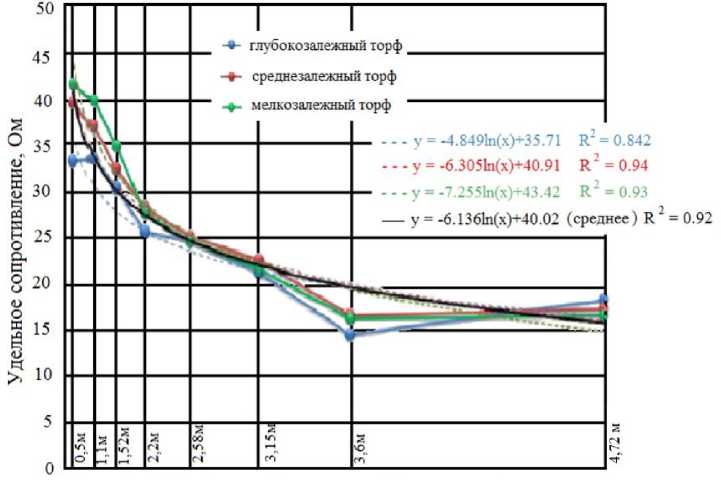
Глубина торфа, м

Рис. 4. Глубина торфа и удельное сопротивление торфа

График показывает, что чем глубже от поверхности, тем ниже удельное сопротивление. Это означает, что удельное сопротивление глубокого горизонта торфа ниже, чем у мелкого горизонта. Объясняется это плотностью материала, потому что глубокий горизонт торфа в основном состоит из плотного с высокой степенью разложения торфа и подстилающего грунта. Чем больше плотность торфа, тем легче проходит электрический ток.

Таким образом, чем выше проводимость, тем ниже удельное сопротивление. Изменчивость толщины торфа на трех участках торфяной залежи (А, В, С) представлена на рис. 4, б .

Сравнив среднее значение удельного сопротивления между глубинами торфа (табл. 2) по статистическому методу ANOVA, получили статистически значимую разницу в удельном сопротивлении.

Таблица 2

ANOVA среднего сравнения по удельному сопротивлению по участкам торфа

Сравнение	Сумма квадратов	df	Среднеквадратическое отклонение	F
Между границами торфяных участков	8387,9	2	4193,9	4,53
В пределах границ торфяных участков	5854862,5	6,323	926,8
Общее	5863250,4	6,324

Таблица 3

HSD Тьюки среднего сравнения по удельному сопротивлению по участкам торфа

Сравнение между участками торфа		Средняя разница	Стандартная ошибка	95%-ная вероятность
				нижняя граница	верхняя граница
А	В	-2,16	0,97	-4,44	0,12
	С	-2,68 *	0,93	-4,85	-0,51
В	А	2,16	0,97	-0,12	4,44
	С	-0,52	0,93	-2,7	1,65
С	А	2,68 *	0,93	0,51	4,85
	В	0,52	0,93	-1,65	2,7

Примечание: каждое значение, сопровождаемое звездочкой, указывает на значительную разницу в разбросе глубины торфа и тенденции отличия удельного сопротивления с глубиной.

2020;5(3):224-234

Таблица 4

ANOVA среднего сравнения по удельному сопротивлению по глубине на каждом участке торфа

Участок торфа	Сравнение	Сумма квадратов	d f	Среднеквадратическое отклонение	F
А	Между глубинами торфа	84481,2	7	12068,7	13,3
	В пределах глубин торфа	1771570,5	1,952	907,6
	Общее	1856051,7	1,959
В	Между глубинами торфа	127238,2	7	18176,9	20,3
	В пределах глубин торфа	1743355,2	1,952	893,1
	Общее	1870593,4	1,959
С	Между глубинами торфа	160056,2	7	22865,2	23,7
	В пределах глубин торфа	1880673,3	1,952	963,5
	Общее	2040729,5	1,959

Таблица 5

Среднее удельное сопротивление по глубине и результат HSD Тьюки для каждого участка торфа

Глубина, м	Участок А	Участок В	Участок С
0,5	33,7	39,9	41,9
1,1	33,9	37,5	40,3
1,52	30,7	32,8	35,3
2,2	26,0	28,6	28,0
2,58	25,1	25,5	24,9
3,15	21,6	22,9	21,9
3,6	14,8	16,9	16,6
4,72	18,6	1,6	16,8

Тест HSD (табл. 3) проводили между участком A (глубокозалежный торф) и участком C (мелкозалежный торф). Однако не отмечается разница между участком А (глубокозалежный торф) и участком B (среднезалежный торф), а также между участком C (мелкозалежный торф) и участком B (среднезалежный торф). Сравнение трех линий показывает, что линия, представляющая глубокозалежный участок (синяя линия) является самой низкой среди других, затем следуют линии среднезалежного участка и линии мелкозалежного участка соответственно. Эта разница объясняется тесной связью с наличием воды в торфе и кислотностью. Толщина торфа сопоставима с его влажностью и кислотностью. Торфяной участок А обводнен больше, чем торфяной участок С. Кроме того, торф на участке А обладает большей кислотностью, и чем больше содержание воды в торфе, тем меньше удельное сопротивление.

Важнейшим результатом являются данные сравнения между глубинами торфа [21]. Когда удельное сопротивление сравнивается между глубинами торфа (табл. 4), также наблюдается статистическая значимость. Разница в удельном сопротивлении между глубинами торфа (р < 0,05) по всем участкам определена с использованием теста Тьюки, результат которого представлен в табл. 5. Результат теста подробно показывает, насколько сильно удельное сопротивление начинает различаться. То есть удельное сопротивление верхнего слоя торфа начинает уменьшаться со значительной разницей по глубине (граница между торфом и подстилающим минеральным грунтом). Таблица показывает, что на участке А удельное сопротивление

I ГОРНЫЕ НАУКИ

I Ж И ТЕХНОЛОГИИ

2020;5(3):224-234

МИСиС

Национальный исследовательский технологический университет

на глубинах 0,5 м, 1,1 м, 1,52 м, статистически не различается, но оно значительно отличается от глубин свыше 4 м. На участке B удельное сопротивление статистически одинаково на глубинах 0,5 м, 1,52 м и 2,58 м и начинает значительно отличаться, когда глубина свыше 3 м. Разница, как показано в статистическом результате теста, тесно связана с характеристиками торфяных участков.

Участок A (глубокозалежный торф) имеет толщину торфа от 3 до 4,72 м – это граница между торфом и минеральным дном. В свою очередь, глубина торфа на участке B (среднезалежный торф) колеблется между 1,5–3 м, поэтому среднее удельное сопротивление имеет тенденцию уменьшаться и существенно различается на уровне 2,8 м. На участке С (мелкозалежный торф) уменьшение удельного сопротивления также происходит на глубине торфяной границы с минеральным дном.

Эти факты указывают на то, что удельное сопротивление измеренное методом VLF, соответствует диапазону торфяных глубин, а значит оно коррелирует с глубиной торфа. Высота удельного сопротивления в верхнем слое (близ- кой к поверхности) по сравнению с глубиной, лежащей дальше от поверхности, очевидна. Обилие содержащейся в торфе органики и наличие воды делают торф более пористым и легким по плотности, чем минеральный грунт. Следовательно, торф имеет тенденцию к снижению проводимости.

Заключение

Метод VLF применим в геофизическом исследовании торфяных месторождений и показывает изменчивость сопротивления торфа по глубинам. Однако более информативно, с точки зрения авторов, было бы использование в качестве дополнения к VLF метода георадиолокации [22, 23]. Удельное сопротивление на основе метода VLF имеет тенденцию уменьшаться по мере роста глубины торфяной залежи. Среднее удельное сопротивление более глубоких горизонтов торфяной залежи значительно ниже, чем поверхностных горизонтов залежи. Вертикальное удельное сопротивление торфа в области глубокозалежного торфа (свыше 3 м) и среднезалежного торфа (1,5–3 м) остается статистически неизменным до глубины, на которой торф превращается в подстилающий минеральный грунт (дно).

2020;5(3):224-234

2020;5(3):224-234

DOI: 10.1016/j.enggeo.2019.105329