Оценка использования нелинейных авторегрессионных нейросетевых моделей для прогнозирования технико-экономических показателей солнечных энергоустановок

В настоящее время для фотоэлектрических систем (ФЭС) оценка техникоэкономических показателей (ТЭП) является актуальной задачей, поскольку, несмотря на непрерывный рост объемов ввода генерации, ФЭС относятся к категории инновационных проектов, имеющих повышенную степень рисков и неопределенности.

Для прогнозирования ТЭП разработаны и активно используются модели ARIMA и GARCH [1-3]. Несмотря на простоту и высокую точность данных моделей, основным недостатком является их линейность, отсутствие возможности учета нелинейного характера отношений между ТЭП. В [4] показано превосходство нелинейных авторегрессионных нейронных сетей с экзогенными входами NARX (neural autoregressive network whith exogenous) над обобщающими моделями авторегрессионной условной гетероскедастичности GARCH.

В работе [5] показано повышение точности прогноза электрической мощности ФЭС за счет использования модели экзогенных факторов - значение годовой нормированной среднеквадратичной ошибки (RMSE) уменьшилось на 1%.

Целью работы является оценка разработанных моделей на основе нелинейных авторегрессионных нейронных сетей с экзогенными входами NARX для прогнозирования электрической мощности и полной приведенной стоимости энергии (LCOE), производимой ФЭС. Результаты прогнозов оценивались по среднеквадратической ошибке (MSE) и по коэффициенту корреляции между результатами и целями (R).

Методы и материалы

Нелинейная авторегрессионная модель с экзогеном NARX описывается следующим уравнением:

y(t) = f(u(t - Du),..., u(t - 1), u(t), y(t - Dy),..., y(t - 1)),           (1)

где: u(t) и y(t) - вход и выход сети в момент времени t ; D_u и D y - порядок ввода и вывода; f – нелинейная функция.

Для прогнозирования электрической мощности P (Вт), ФЭС, разработана двухслойная сеть NARX со скрытыми сигмовидными нейронами и линейными выходными нейронами. Первым шагом в моделировании является создание базы данных (климатические условия Москвы). На вход сети подаются следующие переменные:

• •      Ток короткого замыкания (I sc , А);

• •      Температура окружающей среды (t am , °C);

• •    Суммарная инсоляция (E, Вт/м²).

Указанные выше входные переменные и значения электрической мощности, генерируемой ФЭС, составляют базу данных разработанной сети NARX.

Полная приведенная стоимость электроэнергии LCOE (levelized cost of energy) – отношение полных приведенных капитальных и эксплуатационных затрат к объему выработанной энергии за весь период реализации проекта. Основная расчетная формула LCOE имеет вид [6]:

LCOE =

у n Ct + Cet Lt=1 (1 + d/

у n    Wt '

Lt=1 (1 + d)t

где: Ct - капитальные затраты в год t, $; Cet- операционные затраты в год t, $; PVt - производство электроэнергии в год t, кВт·ч; d – ставка дисконтирования, %; n – жизненный цикл системы.

На вход NARX-сети подаются следующие переменные [7-8]:

• •    объем ввода генерации ФЭС (ГВт),

• •    мировое энергопотребление (ТВт·ч),

• •    потребление нефтепродуктов (млн. т),

• •    потребление природного газа (млрд. м³),

• •    потребление угля (млн. т),

• •    потребление электроэнергии (ТВт·ч),

• •    доля всех возобновляемых источников энергии в мировом производстве электроэнергии (%),

• •    доля ветровой и солнечной энергии в мировом производстве электроэнергии (%),

• •    выбросы CO 2 (млн. т CO 2 ),

• •    цена на нефть Brent к доллару США ($/bbl),

• •    средняя стоимость природного газа ($/BTU).

Разработка прогнозной математической модели базы данных была разделена на два процесса: основной процесс (70% данных) предназначен для обучения сети NARX, процесс тестирования и проверки (30% данных) используется для проверки правильности результаты, чтобы получить представление о распределении данных.

На рис. 1 представлена архитектура разработанных сетей NARX для прогнозирования электрической мощности (а) и LCOE (б) ФЭС.

а)                                      б)

Рисунок 1 - Архитектура NARX-сети для прогнозирования электрической мощности (а) и LCOE (б) ФЭС

Обучение разработанной сети NARX проводилось на основе суточных данных за август для прогнозирования суточного хода электрической мощности и на основе ретроспективных данных за 2005-2010 годы для LCOE. Степень соответствия разработанной NARX данным из обучающего множества определяется интегральным функционалом качества обучения:

N к

E(w) = ^ ^(y (w) - y_t⁾²,                   (3)

1=1 j=i где: к - количество выходов ИНС ПР; N - количество вход - выходных обучающих примеров; (y^ (w) — yt) - вектор отклонения выходов сети от указаний учителя.

Результаты и обсуждение

С помощью разработанных NARX-сетей получен суточный ход электрической мощности, вырабатываемой ФЭС. На рис. 2 показаны результаты прогнозирования электрической мощности ФЭС с использованием разработанной сети NARX для характерного дня августа.

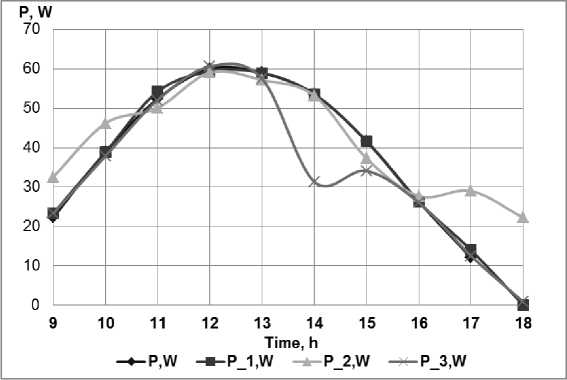
Рисунок 2 - Результаты прогноза электрической мощности ФЭС разработанной

NARX-сетью (август): 1 - включены все переменные; 2 - ток короткого замыкания исключен (I sc); 3 - температура окружающей среды исключена (tam)

Как видно из рис.2 , сеть NARX со всеми включенными экзогенными параметрами имеет наивысшую эффективность. При этом коэффициент корреляции равен R = 0,999, MSE = 0,681, время обучения T = 120 с.

На рис. 3 для сравнения спрогнозированных и фактических данных представлены результаты прогнозирования LCOE ФЭС с помощью разработанной NARX-сети.

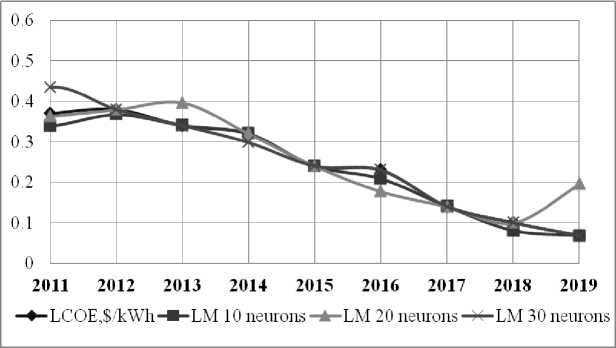
Рисунок 3 - Результаты прогноза LCOE ФЭС с помощью разработанной NARX-сети

Для разработанной NARX-сети для прогнозирования LCOE ФЭС достигнут коэффициент корреляци между результатами и целями R = 0.99904, среднеквадратичная ошибка MSE=0.0042.

Анализ относительной погрешности показал высокую сходимость фактических данных с данными прогноза по электрической мощности и LCOE ФЭС - относительная погрешность составляет не более ± 10%.

Выводы

Таким образом, разработаны математические модели на основе сети NARX для прогнозирования электрической мощности и LCOE ФЭС со значительным приближением (R = 0,999). Разработанные модели могут использоваться при принятии инвестиционных решений при разработке проектов ФЭС для электроснабжения потребителей в агропромышленном комплексе и открывают возможности для эффективной реализации нейросетевого подхода к прогнозированию ТЭП ФЭС.

Благодарности

Работа выполнена при финансовой поддержке ФГБУ «Фонд содействия малым инновационным предприятиям в науке и технологиях» (Фонд содействия инновациям) по договору № 15711ГУ / 2020 (от 11 июля 2020 г.).

Акционерное общество Объединенная энергетическая компания, Россия, 115035, Москва, Раушская набережная, д.8

N. S. Filippchenkova, PhD Joint stock company United Energy Company,