Оценка эффекта от внедрения двухконтурной системы активного контроля и раннего обнаружения "особой" причины изменчивости на операциях механообработки

Для оценки эффективности от внедрения новых средств контроля или модернизации уже имеющегося необходимо выполнение расчётов, позволяющих сравнить преимущества, достигаемые за счёт использования средств контроля [7-8]. Применительно к продукции механообрабатывающего производства можно провести оценку по характеру распределения контролируемых параметров для партии обработанных на данном оборудовании средств контроля [910]. Для сравнения можно воспользоваться моментами распределения, описывающих свойства распределений [1-3].

Первый момент – математическое ожидание или координата центра распределения. В общем случае центр распределения определяется как точка на оси абсцисс, слева и справа от которой вероятность появления различных значений случайной величины равны между собой.

+m

X = J xp ( x ) dx ,             (1)

—M где p(x) - плотность распределения вероятностей.

При дискретных отсчётах, что имеет место в данном случае вместо вычисления интеграла допустимо перейти к вычислению среднего арифметического:

n

X = X -i- .              (2)

i = 1 n

Второй момент – дисперсия случайной величины D , характеризующая рассеяние отдельных значений от центра распределения. Действую-

щее значение рассеяния или среднее квадратическое отклонение является более удобной для оценки характеристикой и имеет размерность случайной величины:

о =

I it ( X - - ) ч D = ', p------ n

Для получения несмещённой оценки дисперсии

– стандартного отклонения пользуются формулой:

5 =

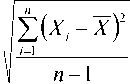
В этой формуле вместо количества образцов n используется количество степеней свободы n-1 . Таким образом, первая формула используется при расчёте по всей генеральной совокупности, во втором случае – по выборке. При этом разница в расчёте не заметна при большом объёме рассматриваемой выборки (больше 100).

Третий момент характеризует асимметрию или скошенность распределения относительно

его среднего значения:

. i "  ( x_t - X Y

A = X I I n i = i I      5      )

.

Клейменов Сергей Иванович, соискатель ученой степени кандидата технических наук, заместитель директора ООО «Бизнес-Консалт», г. Тольятти

Заятров Алексей Викторович, кандидат технических наук.

Чекмарев Анатолий Николаевич, доктор технических наук, профессор.

Седельников Андрей Валерьевич, доктор технических наук, доцент.

На практике для суждения о степени симметричности большее применение имеет безразмерный коэффициент асимметрии, дающий

несмещённую оценку:

n " ( x_t - X Y ³

A =                 X I I .     (6)

( n - 1 ) - ( n - 2 ) i = 1 V 5 )

Четвёртый момент характеризует протяжённость распределения и позволяет оценить величину остроконечности распределения по отношению к нормальному:

£ =

1S f X n^ ( 5

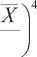
Обычно оценку проводят по коэффициенту эксцесса, который позволяет судить о протяжённости рассматриваемого распределения по отношению к нормальному (для которого £ =3): _£ = n • ( n + 1 ) f X i - X Y _ 3 • ( n - 1 ) 2 (8)

( n - 1 ) ^ ( n - 2 ) ^ ( n - 3 ) i = 1 ( 5 J ( n - 2 ) ^ ( n - 3 ) ^.

Испытания выполнялись на оборудовании одного из ведущих российских предприятий по выпуску автомобилей, в частности круглошлифовальном станке производства завода Livnica Kikinda, для наружной шлифовки. На указанном оборудовании выполняется обработка детали с допуском: Ø27^-0,015 – 27^-0,036 мм. Результаты замеров до модернизации и после сведены в таблицу 1. Показатели отмеченные знаком « ‘ » относятся к данным, полученным на оборудовании до модернизации.

На рисунках 1 и 2 представлены гистограммы размеров обработанных на шлифовальном станке деталей с наложенным графиком функции плотности распределения вероятностей нормального закона со старым средством контроля и с использованием двухконтурной структуры активного контроля соответственно. Помимо замены самого средства активного контроля дополнительно проводились работы по модернизации шлифовального станка. Дополнительно в таблицу 2 сведены статистические показатели полученных результатов. Все значения размера обработанных деталей представлены в относительном виде относительно центра поля допуска на обрабатываемую деталь – 26,975 мм.

Анализ рисунков 1 и 2, а также данных в таблице 2 показывает положительный эффект от результатов модернизации контрольного оборудования и модернизации оборудования. В

Таблица 1. Результаты испытаний средств контроля

№ детали	Время'	L 2 , мкм	T ′ os , Сек	Время	T os , Сек	V MK , мкм/сек	L 2 , мкм
1	12:29	8	25,5	10:18	27,4	13,2	0
2	12:31	11	25,9	10:19	29	9,4	4
3	12:34	7	25,6	10:21	28,3	10,3	4
4	12:35	9	25,5	10:22	28,3	11,6	4
5	12:37	3	23,4	10:23	27,9	11,9	2
6	12:38	5	25,6	10:24	28	12,2	2
7	12:39	5	25,7	10:32	28,3	11,9	3
8	12:40	6	26,2	10:33	28,1	11,0	2
9	12:41	8	26	10:34	28,2	11,0	4
10	12:42	7	25,8	10:35	28	12,2	4
11	12:43	6	25,7	10:36	27,8	12,7	1
12	12:44	7	26	10:37	28,7	8,2	4
13	12:46	4	25,5	10:38	28,4	10,8	3
14	12:47	5	25,3	10:40	25,8	12,4	4
15	12:49	1	23,2	10:41	28,3	10,4	2
16	12:50	4	26,1	10:42	28,6	9,7	5
17	12:51	5	25,8	10:43	28,2	11,7	3
18	12:52	3	26	10:44	28,5	8,7	4
19	12:53	7	26,2	10:45	28	11,9	2
20	12:54	1	26,2	10:46	28,2	11,3	3
21	12:55	4	26,3	10:47	28	11,9	2
22	12:56	7	26,2	10:52	28,1	11,6	3
23	12:57	6	26	10:53	28,3	10,0	4
24	12:58	5	26	10:54	28,3	10,5	2
25	13:00	2	23,8	10:55	27,6	13,5	1
26	13:01	0	25,5	10:57	28,3	10,8	4
27	13:02	5	26	10:58	28	11,8	2
28	13:03	3	25,4	10:59	28	13,7	0
29	13:04	6	26,3	11:00	27,9	11,9	1
30	13:05	5	26,3	11:10	28,3	11,4	4

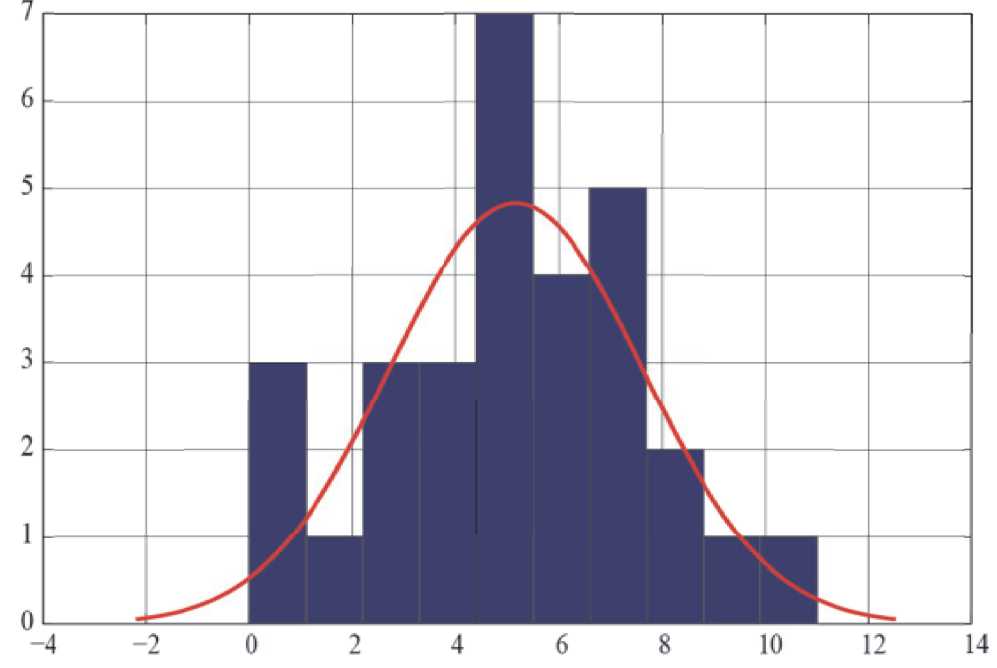
Рис. 1. Гистограмма распределения замеров на этапе послеоперационного контроля до модернизации оборудования

Таблица 2. Статистические показатели

Наименование показателя	Значение до модернизации	Значение после модернизации
Максимальное значение в выборке	11,0	5,0
Минимальное значение в выборке	0,0	0,0
Среднее арифметическое выборки	5,17	2,77
Стандартное отклонение	2,45	1,33
Коэффициент асимметрии	-0,04	-0,48
Коэффициент эксцесса	0,25	-0,64

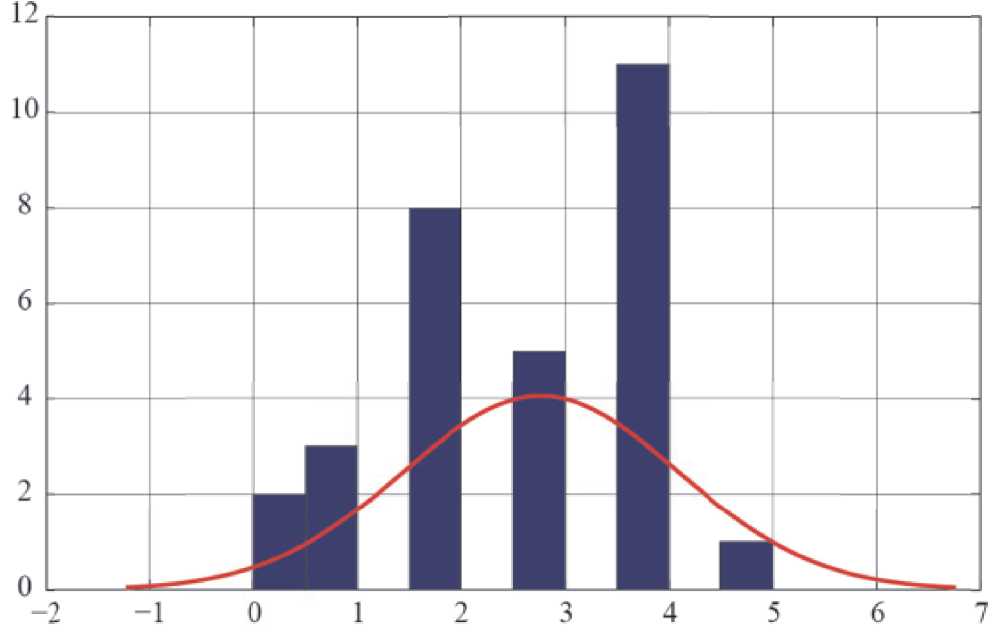
Рис. 2. Гистограмма распределения замеров на этапе послеоперационного контроля после модернизации оборудования

частности, более чем в 2 раза сократилось величина рассеяния итогового размера детали от центра распределения, а также сам центр распределения сместился ближе центру поля допу- ска контролируемого параметра. Коэффициент асимметрии говорит о большем, чем до модернизации смещении результатов относительно среднего значения влево. Коэффициент эксцес- са также увеличился и сменил знак по отношению к первоначальному, что свидетельствует о снижении величины остроконечности по отношению к нормальному закону распределения. Таким образом, для дальнейшего смещения центра распределения к центру поля допуска контролируемого параметра требуется провести ряд дополнительных настроек.

Выявив положительный эффект от модернизации используемого оборудования определим возможность раннего выявления момента разладки технологического процесса. Для этого сопоставим данные, получаемые на этапе активного контроля основного контура в темпе технологического процесса – конечную скорость снятия припуска в момент окончания обработки, с реальным размером детали, получаемым на этапе послеоперационного контроля дополнительного контура [4 – 6].

Для этого воспользуемся данными таблицы 1 и рассчитаем отклонение конечной скорости снятия припуска Δ V_МК , в качестве номинального значения выбрав среднее:

^A V MKi = V MKi - V^MK . (9)

А также отклонение размера детали Δ L ₂ для каждой детали:

∆ L _{2 i} = L _{2 i} - L 2 . (10)

Результаты представлены на рисунке 3.

В подобном виде диаграммы малоинформативные и по ним сложно судить о степени соответствия между данными, получаемыми в темпе технологического процесса и в статических условиях дополнительного контура. Проведём простейшую статистическую обработку методов контрольных карт средних и размахов по 3

детали в выборке, результаты проиллюстрированы на рисунке 4.

Анализ контрольных карт, представленных на рисунке 4, уже достаточно информативен и позволяет отследить общие тенденции на обоих графиках, в особенности для карты средних. Коэффициент корреляции, рассчитанный для значений отклонения конечной скорости снятия припуска и отклонения размера детали, можно определить по следующему выражению:

E ^{( a L} 2 i - ^A L ² ) ■ ^{( a} V MKi ^{-A V mk} )

R = j П ^{= 1}                   n                       ^;.(ii)

J E (AL2i -AL2 )2 ■ E (A VMKi -AVmk У i =1                                 i=1

Коэффициент корреляции получился R =–0,8987, что подтверждает высокую степень связи между анализируемыми параметрами. В этой связи можно рассчитать коэффициенты аппроксимирующего выражения для отклонения размера через показатели отклонения конечной скорости съёма припуска, которое будет иметь вид:

AL = A1 ■A Vmk + A 2,       (12)

где А ₁ и А ₂ – постоянные коэффициенты, для конкретного оборудования и параметров обработки.

В рассматриваемом случае выражение (12) примет вид:

a l = - 0,769 ■a V _mk - 0,01 ,      (13)

Представим на одном графике (рисунок 5) контрольную карту средних значений отклонения размеров деталей, полученных непосредственно в дополнительном контуре Δ L ₂ с отклонением размеров деталей, рассчитанных по

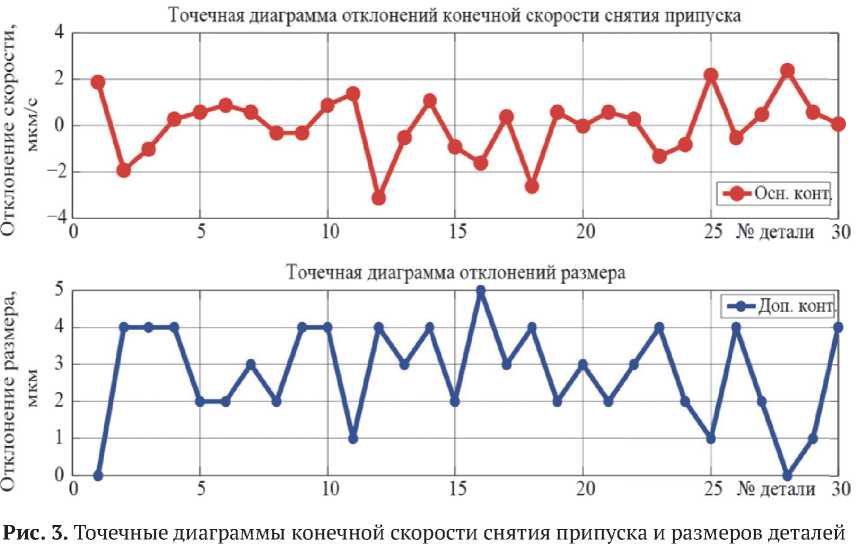
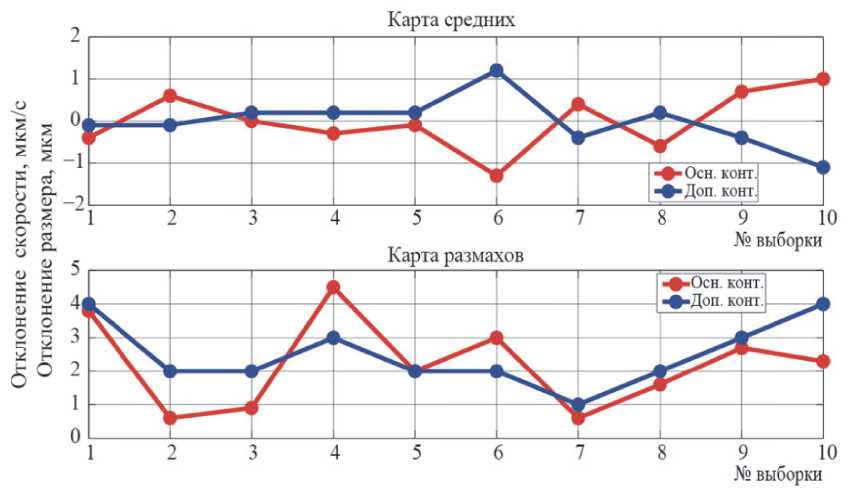
Рис. 4. Контрольные карты средних и размахов для отклонения скорости и размера

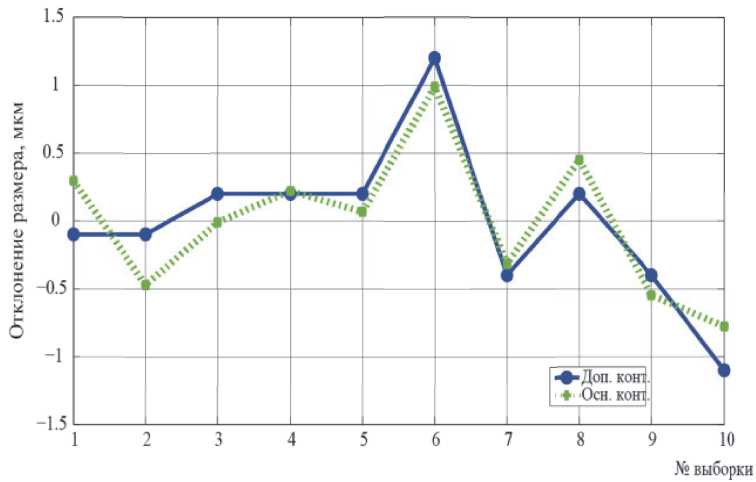
Рис. 5. Карта средних значений отклонения размера деталей для основного Δ L ₁ и дополнительного Δ L ₂ контуров

выражению (13) на основе отклонения конечной скорости снятия припуска в момент окончания обработки в основном контуре Δ L ₁ .

Как видно из сравнения представленных графиков рассчитанные значения отклонения размера детали в основном контуре хорошо повторяют результаты статического контроля дополнительного контура. Максимальные расхождения между отклонением размера, полученном в динамическом режиме и статическом режимах прослеживаются только на первых двух выборках, достигая максимальной разницы в 0,4 мкм.

Таким образом, данные получаемые в темпе технологического процесса могут быть использованы для оценки качества готовых деталей, являясь довольно точным показателем отклонения геометрических параметров детали от номинального значения. Также это позволит использовать данные параметры для раннего обнаружения причин изменчивости, выводящих технологический процесс из устойчивого состояния.

Стоит отметить, что величины погрешности обработки ΔL, даже при постоянстве времени отвода шлифовального круга в момент окончания обработки, близки к результатам, полученным во втором контуре системы контроля только в случае больших значений конечной скорости снятия припуска VМК. Если значения VМК находятся в диапазоне от 5 мкм/с и выше, то совпадение динамической погрешности размера, полученное в основном контуре с результатами статических измерений в дополнительном контуре велико. В случае, когда значения VМК находятся в диапазоне до 5 мкм/с, что часто имеет место в производственной практике, увеличивается доля влияния прочих возмущающих факторов – температурный режим обработки, состояние шлифовального круга и периодичность его правки, качество СОЖ и её количество, поступающее в зону обработки. В подобных ситуациях требуется контроль дополнительных факторов для более точных вычислений.

Помимо проблемы повышения качества выпускаемой продукции в направлении увеличения точности обработки, особенно при модернизации уже имеющегося оборудования возникает вопрос об экономической целесообразности подобных улучшений. Современные приборы как активного, так и послеоперационного контроля в совокупности с измерительной оснасткой (измерительное приспособление, датчики контроля, эталоны и т.п.) стоят довольно дорого. Помимо стоимости самих приборов необходимо учитывать затраты, связанные с их обслуживанием в период эксплуатации (ремонт, настройка и калибровка). Если вопрос о целесообразности установки на новом оборудовании, впервые вводимом в эксплуатацию, средств активного и послеоперационного контроля не встаёт, то при модернизации он чрезвычайно актуален. Для этого проводится экономический расчёт, причём оцениваются показатели как для уже функционирующего оборудования, так и для нового с тем, чтобы сопоставить разницу между текущими показателями и величиной положительного эффекта, который может быть достигнут после внедрения новых средств контроля.