Оценка эффективности фракционирования дозы в лучевой терапии злокачественных новообразований по критерию ранних лучевых реакций

Один из способов повышения эффективности лучевой терапии (ЛТ) злокачественных новообра‑ зований состоит в оптимизации режимов фракцио‑ нирования дозы, поиск которых является важной задачей [1–6]. Для ее решения применяют клиниче‑ ские [1, 2] и радиобиологические исследования [3], а также математическое моделирование [4–7]. На основе линейно‑квадратичной модели (ЛКМ) по‑ лучены математические выражения, позволяющие выбирать режимы фракционирования дозы, обе‑ спечивающие одинаковую предельно допустимую степень поражения нормальной ткани [4–6]. Одна‑ ко поскольку облучаемые опухоли и нормальная

ткань характеризуются различными радиобиологи‑ ческими параметрами, режимы фракционирования дозы, обеспечивающие предельно допустимую степень поражения нормальной ткани, ведут к раз‑ личной степени регрессии одной и той же опухоли. Для того чтобы из большого числа возможных режимов фракционирования дозы, приводящих к одинаковой и допустимой степени поражения нормальной ткани, выбрать такой, который приво‑ дит к максимальной степени поражения опухоли, необходимо знать характер регрессии опухолей в зависимости от режимов фракционирования дозы. Возможность применения ЛКМ для исследования регрессии опухолей при одинаковой предельно допустимой степени поражения нормальной ткани ранее не рассматривалась.

Цель исследования – изучить закономерности регрессии опухолей при различных, но обеспечива‑ ющих одинаковую степень поражения нормальной ткани режимах фракционирования дозы в случае, когда реакция нормальной ткани и выживаемость облучаемых клеток опухоли могут быть описаны линейно‑квадратичной моделью.

Материал и методы

При любом режиме фракционирования дозы в ЛТ должен быть обеспечен приемлемый уро‑ вень частоты и выраженности лучевых реакций. Значительный период времени инструментом, обеспечивающим указанное условие, являлась кон‑ цепция Ellis, которую можно описать следующей эмпирической формулой:

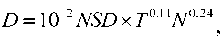
где D – суммарная доза курса терапии, Гр; NSD – номинальная стандартная доза; Т – длительность курса (сут); N – число сеансов.

Согласно (1), допускается множество режимов облучения, каждый из которых приводит к оди‑ наковой степени поражения нормальной ткани. Концепция Ellis и ее модификации не утратили своего практического значения и в настоящее вре‑ мя [9], однако на смену ей приходит ЛКМ, согласно которой выживаемость клеток при однократном облучении может быть описана выражением

S = S„eypHad^ Pd"^ , (2)

где S_oи S – соответственно начальное число клеток и число клеток, выживших после облучения дозой d ; α и β – параметры модели, причем параметр α определяет долю летальных повреждений в клет‑ ках и выражается в Гр^‑1, параметр β определяет долю накапливаемых сублетальных повреждений и имеет размерность Гр^‑2.

При планировании ЛТ по ЛКМ принимают [4, 5], что внутриклеточная репарация в нормальных тканях осуществляется полностью за время ин‑ тервала между фракциями, а пролиферация вы‑ живших клеток в течение курса лучевой терапии не учитывается.

Для достижения сформулированной в статье цели необходимо иметь два уравнения, описываю‑ щих реакцию нормальной и опухолевой тканей на фракционированное облучение. С учетом (2) и приведенных выше допущений соответствующую систему уравнений можно записать в виде:

S™ = SOHm ^[-N(amd+0md2y\

,          ,     (3)

Son = So,oneypV-N<.aond^Pond^*(pTA где αнт, βнт и αоп, βоп – параметры ЛКМ, характери‑ зующие радиочувствительность соответственно нормальной и опухолевой ткани; φ – параметр, учитывающий скорость восстановления клеточно‑ го пула опухоли между сеансами терапии.

Система справедлива для случаев, когда разовые дозы в опухоли и нормальной ткани равны. Такое возможно при облучении поверхностных новооб‑ разований с одного поля или при многопольном облучении глубоко расположенных опухолей. В этих случаях нормальная ткань, являющаяся критической, и опухоль, как правило, облучаются одной и той же дозой.

Одно из преимуществ ЛКМ состоит в воз‑ можности контролировать с ее помощью частоту ранних (РЛР) и поздних лучевых реакций (ПЛР) [4–6]. В данной работе исследованы режимы фрак‑ ционирования дозы, обеспечивающие допустимую частоту РЛР. Заметим, что именно для этого ва‑ рианта накоплено значительное число достовер‑ ных клинических данных, поскольку несколько десятилетий планирование ЛТ проводилось на основе концепции Ellis, ориентированной именно на прогнозирование РЛР.

Для расчета выживаемости опухолевых клеток при режимах фракционирования, приводящих к одинаковой и допустимой степени поражения нормальной ткани, необходимо установить со‑ ответствующую функциональную связь между однократной дозой d и числом сеансов терапии N. Известно [4, 5], что допустимую частоту РЛР обеспечивает стандартный (классический) режим фракционирования дозы, характеризуемый пара‑ метрами: d=2 Гр, N=30, Т=40 сут. В работе [10] нами определены параметры ЛКМ для нормаль‑ ной ткани в ЛТ редкоионизирующим излучением: αнт=0,25 Гр‑1; βнт=0,025 Гр‑2. С помощью приведен‑ ных данных по первому уравнению системы (3) можно установить, что доля выживающих клеток нормальной ткани 5 = при стандартном $О,нт курсе ЛТ составляет ~1,5×10‑8. При планировании ЛТ по JIKM исходят из предположения, что если в тканях, облученных при различных режимах фракционирования дозы, наблюдаются аналогич‑ ные лучевые реакции, то доля выживших клеток в них должна быть одинаковой [5]. Поэтому для того, чтобы все исследуемые режимы фракцио‑ нирования обеспечивали допустимую частоту и выраженность РЛР, для каждого из них необходимо выполнить условие:

s = exp Y-N^a^d + P_Hm d²)] = const = 1,5 x 10"⁸ . (4)

Логарифмируя (4), получим:

|1п5| = ^со/ + Д/²) = 18 . (5)

Выразив из (5) d, найдем взаимосвязь между d и N для изоэффективных режимов фракциониро‑ вания для нормальной ткани:

^ = 5[(1 + 28,8/^°’5-1]. (6)

Уравнение (6) устанавливает связь между па‑ раметрами d и N для режимов фракционирования, приводящих к предельно допустимой степени РЛР.

Представляет интерес сравнение однократных доз, допускаемых концепцией Ellis и ЛКМ, для стандартной длительности курса, равной 40 сут, при различном числе сеансов терапии. Выражение для допустимых однократных доз по концепции Ellis с учетом (1) будет иметь вид d = \^NSDxTwN-o;16. (7)

Результаты расчета зависимостей по (6) и (7) представлены на рис. 1: точки – расчет по (6), линия – расчет по (7). Видно, что графики хорошо совпа‑ дают между собой, что свидетельствует, с одной стороны, о преемственности ЛКМ по отношению к концепции Ellis, а с другой – о корректности по‑ лученного выражения (6).

Подставив выражение (6) для разовой дозы d во второе уравнение системы (3), можно рас‑ считать зависимость выживаемости опухолевых клеток при различных, но эквивалентных по свое‑ му воздействию на нормальную ткань режимах фракционирования дозы. В расчетах принято, что указанные выше значения параметров ЛКМ для нормальной ткани сохраняются для всех рассмо‑ тренных ниже режимов фракционирования дозы. Начальное число клеток облучаемой опухоли в расчетах So=1010. Значения параметра φ, учиты‑ вающего восстановление клеточного пула опухоли между сеансами терапии, находятся, по литератур‑ ным данным [11], в широких пределах, а именно: 0,05 сут‑1≤φ≤0,001 сут‑1. Поскольку наибольшую опасность для больного представляют быстрора‑ стущие опухоли, то нами при моделировании ЛТ в общих случаях принято значение φ=0,05 сут‑1, соответствующее таким опухолям. При сравнении результатов моделирования с известными клиниче‑ скими данными для оценки влияния параметра φ на характер режима фракционирования дозы рас‑ смотрена выживаемость клеток опухоли при двух его значениях. Для карциномы легкого, согласно [11, 12], значения параметров φ приняты равными 0,04 сут‑1 и 0,01 сут‑1, а для меланомы, по данным работы [13] и рекомендациям [11], взяты значения φ=0,1 сут‑1 и φ=0,01 сут‑1. При выборе параметров φ для меланомы учтено также, что, согласно [11, 12], для первичных опухолей и их метастазов эти величины близки по своим значениям.

Результаты и обсуждение

В исследованиях рассмотрены варианты с раз‑ личными количественными соотношениями между параметрами α и βдля опухоли и нормальной тка‑ ни, далее п.п. I, II, III .

• I.    α_оп/β_оп= α_нт/β_нт = 10 Гр.

В свою очередь, условие « I » также может быть соблюдено при различных соотношениях между радиочувствительностью опухоли и нормальной ткани. Рассмотрены три возможности: 1) нормаль‑ ная ткань радиочувствительнее опухоли; 2) их радиочувствительность одинакова; 3) опухоль радиочувствительнее нормальной ткани.

Параметры опухоли выбраны следующими: 1) αоп = 0,2 Гр‑1; βоп = 0,02 Гр‑2; 2) αоп = 0,25 Гр‑1; βоп= 0,025 Гр‑2; 3) αоп= 0,35 Гр‑1; βоп= 0,035 Гр‑2. При заданных параметрах проведен расчет выживае‑ мости клеток опухолей при фракционированном облучении, результаты которого представлены на рис. 2. По графикам видно, что, с одной стороны, наблюдается очевидная закономерность, состоя‑ щая в том, что эффективность ЛТ для опухоли с большей радиочувствительностью (зависимость 3) выше, чем для более радиоустойчивых опухолей (зависимости 1, 2). С другой – обнаружена не от‑ мечавшаяся ранее закономерность, состоящая в том, что при условии αоп/βоп=αнт/βнт эффективность лучевой терапии не зависит от режима фракцио‑

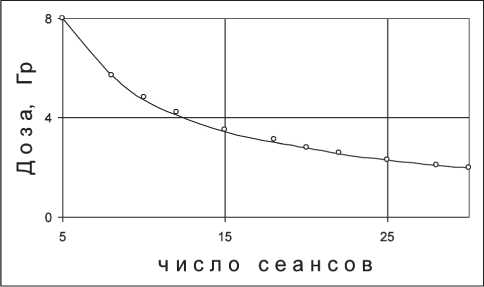
Рис. 1. Зависимости однократной дозы от числа сеансов терапии при Т=40 сут по ЛКМ и Эллис

о 1,E+07--1------------ i—

Ф

1 ,E+04--2------------ о q 1.E+01 -

^         ---------------------3----------- т 1.E-02-I-----------1-----------1-----------1-----------1-----------

5     10     15    20    25    30

число сеансов

Рис. 2. Выживаемость клеток при фракционированном облучении, αоп/βоп=10 Гр

нирования дозы при любом соотношении между радиочувствительностью опухоли и нормальной ткани.

• II.    25™ = 15 Гр , то есть ^оп \ ^н.т. .

Ро„.                     Рои. Р™.

Конкретные значения радиобиологических параметров опухоли для варианта « II » приняты следующими: 1) α_оп= 0,25 Гр^‑1; β_оп ≈ 0,017 Гр^‑2; 2) α_оп= 0,375 Гр^‑1; β_оп= 0,025 Гр^‑2.

В случае «II–1» увеличение отношения αоп/βоп по сравнению с αнт/βнт достигается за счет уменьшения βоп при сохранении значения αоп= αнт, в случае «II–2» – за счет увеличения αоп при сохранении значения βоп=βнт. Результаты расчета выживаемости клеток опухолей с параметрами «II–1» и «II–2» при фрак‑ ционированном облучении представлены на рис. 3.

Видно, что при        эффективность ЛТ

Рои. Рнлп.

зависит от режима фракционирования дозы и по‑ вышается при увеличении числа сеансов терапии, т.е. при уменьшении дозы за фракцию.

• III.    , то есть ^,

Конкретные значения параметров α и β для опу‑ холи следующие: 1) αо = 0,15 Гр‑1; βо = 0,025 Гр‑2; 2) αоп= 0,25 Гр‑1; βоп= 0о,п042 Гр‑2. оп

В случае «III‑1» уменьшение отношения α_оп/β_оп по сравнению с α_нт/β_нт достигается за счет умень‑ шения α_оп при сохранении значения β_оп= β нт , а в случае «III–2» – за счет увеличения β_оп при со‑ хранении значения α_оп=α_нт. Кривые выживаемости при фракционированном облучении для клеток с параметрами «III–1» и «III–2» показаны на рис. 4.

а .а

По графикам видно, что в случае, когда on н.т.

обнаруживается закономерность, противополож‑ ная наблюдаемой в случае « II », а именно: эффек‑ тивность ЛТ возрастает при уменьшении числа сеансов, т.е. при повышении однократной дозы.

Отсутствие зависимости эффективности ЛТ от режима фракционирования дозы при αоп/βоп= αнт/βнт (рис. 2) и относительно слабая ее зависимость, показанная на рис. 3 и 4 для

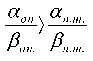
и

,

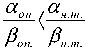
в некоторой степени объясняют трудности по‑ иска оптимальных режимов фракционирования дозы для большинства типов злокачественных новообразований.

Представляют интерес закономерности фракци‑ онирования дозы для конкретных типов опухоли. В данном случае в качестве примера нами взяты карцинома легкого и меланома. Для проведения расчетов необходимо знать параметры ЛКМ, со‑ ответствующие названным опухолям. Поскольку в литературе ограничиваются сведениями только об отношении α/β, нами для определения в от‑ дельности параметров αоп и βоп применен подход, изложенный ранее в работе [10]. В основе под‑ хода лежит сравнение выживаемости клеток при однократном облучении, описываемом по ЛКМ и многомишенной модели. При использовании ука‑ занного подхода определены параметры α и β для карциномы легкого (αоп=0,482 Гр‑1; βоп=0,0327 Гр‑2, αоп/βоп ≈15 Гр) и меланомы (αоп=0,048 Гр‑1; βоп=0,051 Гр‑2; αоп/βоп=0,95 Гр). Найденное соотношение αоп/ βоп для карциномы легкого находится в пределах, приведенных для нее в [4]. Карцинома легкого является высокорадиочувствительной опухолью, поэтому в расчетах для нее принято So=1012. От‑ ношение αоп/βоп для меланомы также удовлетвори‑ тельно согласуется с данными работы [4], согласно которой эта величина равна 0,6 Гр. Известно, что карцинома легкого относится к радиочувствитель‑ ным, меланома – к радиоустойчивым опухолям, о чем и свидетельствуют характеризующие их радиобиологические параметры.

На основе найденных параметров для карцино‑ мы легкого (рис. 5) и меланомы (рис. 6) рассчитана выживаемость клеток этих новообразований при фракционированном облучении как функция числа сеансов терапии при постоянной длительности курса терапии, равной 40 сут, и двух значениях параметра φ. На рис. 5 видно, что для карциномы легкого эффективность лучевой терапии растет с увеличением числа фракций, т.е. с уменьшением

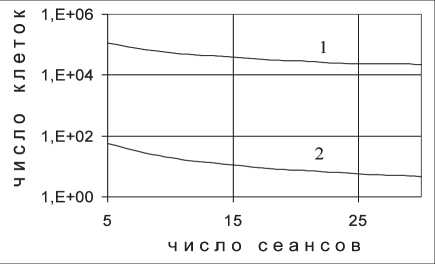
Рис. 3. Выживаемость клеток при фракционированном облучении, αоп/βоп=15 Гр

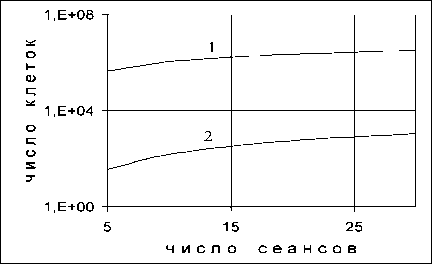
Рис. 4. Выживаемость клеток при фракционированном облучении, αоп/βоп=6 Гр

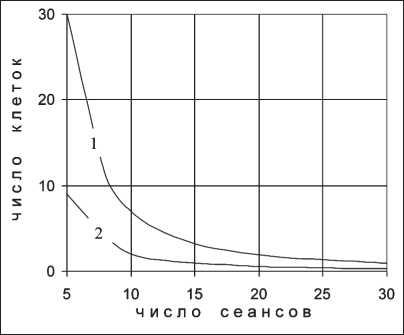
Рис. 5. Выживаемость клеток карциномы легкого при фракционированном облучении для ф = 0,04 сут^-1 (1) и ф = 0,01 сут^-1 (2)

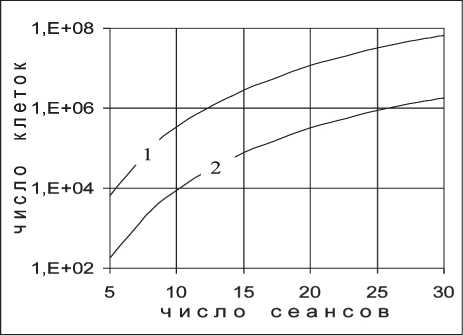
Рис. 6. Выживаемость клеток меланомы при фракционированном облучении для ф = 0,1 сут^-1 (1) и ф = 0,01 сут^-1 (2)

дозы за фракцию. Полученный результат согласу‑ ется с зависимостями, представленными на рис. 3, поскольку для обоих рисунков выполняется условие . Наблюдается согласие и с из‑ Р on. Рн.т.

вестными клиническими данными работы [14], в которой приведены результаты лучевой терапии у 262 больных неоперабельным эпители‑ альным раком легкого при различных вариантах фракционирования дозы: облучение проводилось 31 фракцией по 2 Гр, 18 фракциями по 3 Гр, 12 фракциями по 4,05 Гр за 37 дней и 6 фракциями по 6,8 Гр за 35 дней. В работе сказано, что при всех вариантах фракционирования суммарные очаговые дозы, согласно концепции Ellis, были эк‑ вивалентны по своему воздействию на нормальную ткань. Это подтверждается тем, что оценка для всех четырех приведенных режимов фракционирования фактора «время – доза – фракционирование» (ВДФ) по формуле

ВДФ = 1,2 х TV х d¹’⁵³⁸ X (ДТ)’⁰’¹⁶⁹

дает приблизительно одно и то же значение: 100÷104 ед. Следовательно, в клинических исследованиях [14] выполняется то же условие, что принято и в наших расчетах: все примененные режимы фракцио‑ нирования эквивалентны по своему воздействию на нормальную ткань по критерию ранних лучевых ре‑ акций. При анализе результатов лечения авторами работы [14] показано, что эффективность лучевой терапии повышается с увеличением числа фрак‑ ций, а лучший эффект по критерию локального из‑ лечения получен при использовании однократной дозы 2 Гр при 31 сеансе терапии, что согласуется с полученным нами теоретическим результатом.

Для меланомы (рис. 6), как и в случае «III», выполнятся условие

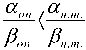
, поэтому повыше‑ ние эффективности лучевой терапии для этого типа опухоли наблюдается при уменьшении числа сеансов терапии, т.е. с увеличением однократной дозы. Однако, поскольку для меланомы отношение

06 on существенно меньше, чем для опухолей, рас‑ смотренных в случае «III», зависимость выживае‑ мости клеток меланомы при фракционированном облучении выражена более существенно, чем на рис. 4.

Полученный теоретический результат для мела‑ номы хорошо согласуется с известными результата‑ ми, полученными непосредственно в клинических исследованиях [15]. Авторами проанализированы данные по лучевой терапии 36 пациентов с реци‑ дивами и метастазами меланомы при различных режимах фракционирования дозы. В упомянутом исследовании все полные курсы терапии приво‑ дят к одинаковой предельно допустимой степени поражения нормальной ткани по критерию ран‑ них лучевых реакций, поскольку оно проведено в рамках концепции Ellis. В работе сказано, что выбранный режим фракционирования «позволяет проводить облучение с умеренно выраженными явлениями местной лучевой реакции» .

При анализе результатов установлено [15], что наиболее эффективными являются курсы лучевой терапии с меньшим числом фракций и, следова‑ тельно, с большей дозой за фракцию, а именно: лучший эффект дает облучение фракциями по 8 Гр и более, что согласуется с полученным нами теоре‑ тическим результатом, приведенном на рис. 6.

Сравнение зависимостей (1) и (2) на рис. 5 и рис. 6, полученных при различных значениях пара‑ метра φ, показывает, что скорость восстановления клеточного пула опухоли не влияет на характер фракционирования дозы. Для обоих значений φ эффективность ЛТ для карциномы легкого повы‑ шается с уменьшением однократной дозы, а для меланомы в обоих случаях повышение эффек‑ тивности ЛТ происходит с ее увеличением. При этом и для карциномы легкого, и для меланомы эффективность ЛТ выше при больших значениях параметра φ, т.е. при меньшей скорости восстанов‑ ления клеточного пула.